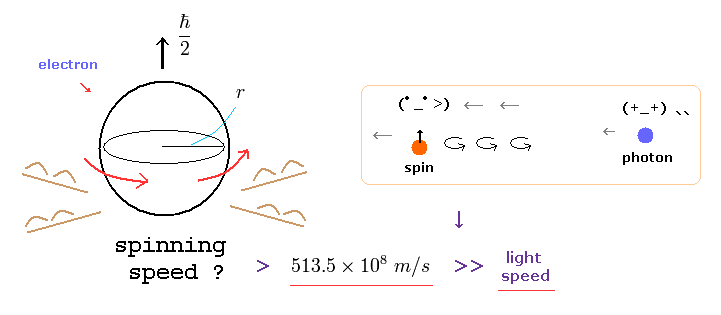
トップページ (2電子原子も含む正確な新ボーア模型)
フェルミの黄金律と統計の導出。
物性物理学のスピントロニクスは 幻想である。
(Fig.1) 電子のスピン回転速度は 光速を はるかに超えている。
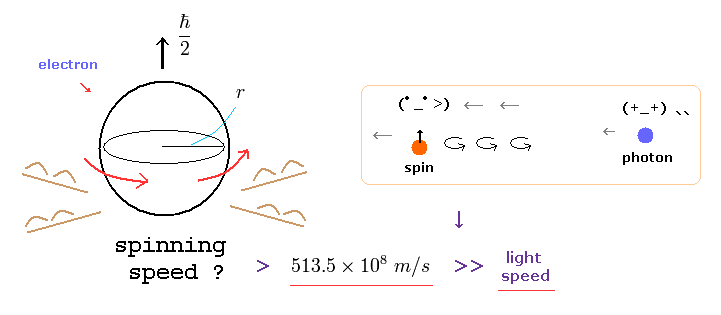
実際の実験によれば、単一の電子は 点状粒子のように 非常に小さい。
しかし 量子力学は この点状の電子は 1/2 ħ の角運動量を持っていると主張している。
ご存じの通り、角運動量は mv× r である ( m= 電子質量、 v=回転スピード、 r =電子の半径 )。
電子の 非常に小さな質量と半径を考慮すると、この回転スピードは
光速の 100 倍以上にならないと 1/2 ħ の角運動量に到達しない ( このページも参照のこと )。
これはつまり 量子力学のスピンは 非現実的で かつ 想像上の産物であることを示している。
(Fig.2) パウリの排他原理の原因は "力" ? → "つまらんことは質問するな。"
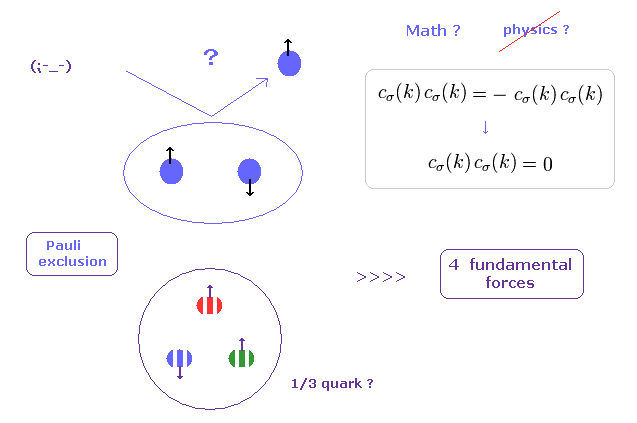
何かしらの物性物理学の教科書を見れば分かるが、一見して それらの本の中には 非現実的な "スピン" の語句で溢れかえっているのが分かる。
その主要な要因は "パウリの排他原理" にあると言っていい。つまり 2つの同じ状態のフェルミ粒子は 同じ場所に入れない。
( しかし この”同じ場所”という定義が 非常に曖昧である。物理的に 境界線を はっきり定めることもできないのに。)
例えば、1s エネルギー準位では スピン "up" と "down" の電子のみしか 入れない。
彼らは クォークにおいてさえ パウリの排他原理を強引に満たすため 非常に人為的な "カラー" (= 赤、青、緑 ) なる概念を導入した。
つまり この謎めいたパウリの排他原理を引き起こす"力"というのは 他の4つの基本的な力よりも はるかに強力なものと言える。
問題は 物理学者達は 決して このパウリの排他原理の実態を 21 世紀になった今でさえ 調べようとしないことである。
莫大な経費を 役に立たない 非常に高価な加速器なんかに浪費する前に このパウリの排他原理の正体を 真先に調べるのが 道理であろう。
(Fig.3) 単なる抽象的な 演算子では バライティーに富む 実際の現象を説明できない。
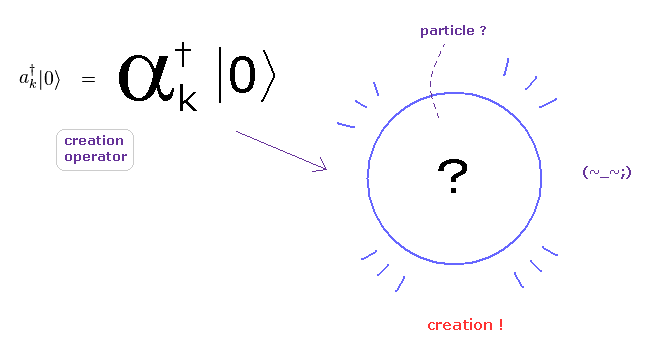
現在の物性物理学、標準模型、ひも理論などの量子論では 様々な物理現象を記述するのに 非常に抽象的な演算子なるものに 完全に頼っている。
このページに見られるように、これらの生成消滅演算子では 実世界の 様々なダイナミックに変化する現象を記述するには どう転んでも 限界がある。
なぜなら これらの生成 (消滅) 演算子では ただ漠然と 空間上に 粒子が生成 (消滅) したことのみを示せるだけで、具体的な変化に富む 時間、場所、位置関係を指定できないからである。
つまり、これらの非常に抽象的な演算子 (+ スピン ) こそが 現在の科学の発展を妨げる 最大の要因である。
(Fig.4) 現実の変化に富む世界は 単純な数学上の模型とは違いすぎる。
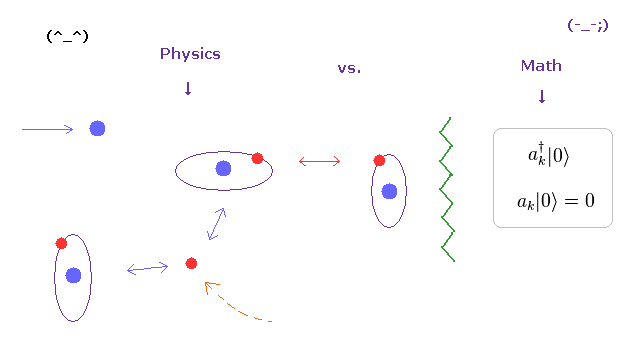
実世界の様々な物理現象、しいては 非常に複雑な 私達人間の高度な生体システムを見て分かるとおり、電子や陽子などの粒子は 実際には 複雑かつ ダイナミックに 動き回っている。
そして それらの粒子が相互作用するタイミングや その時の 微妙な位置関係の違いなどが バライティーに富む 様々な生体機能を決定していると言える。
残念ながら "a†" や "a" などの 単なる抽象的な数学の記号のみでは これらの複雑かつ変化に富む機能を説明することは 不可能である。
(Fig.5) スピン・スピン相互作用は 非現実的なぐらい弱い。
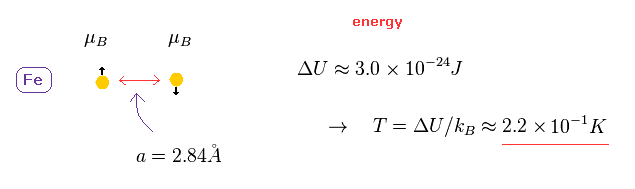
強磁性などは 金属における スピン・スピン相互作用によって生じると言われている。
しかし 実際には このスピン磁気モーメントが 室温で 強磁性を引き起こすには あまりにも弱すぎるのである。
鉄の格子定数は 2.84 Å である。
この距離では スピンが平行、反平行の状態の間のエネルギー差は Fig.6 に示したように
非常に小さい。
ボルツマン定数 k を用いれば、このエネルギー差は たったの 0.22 ケルビンである。( このページも参照のこと。 )
そのため スピン・スピン相互作用が それらの磁気モーメントによって生じるとしたら、磁石は 室温で 簡単に壊れてしまうことになる。
(Fig.6) 弱い "スピン" が 必ず 他のスピンを平行、反平行にそろえるのは 本当 ?
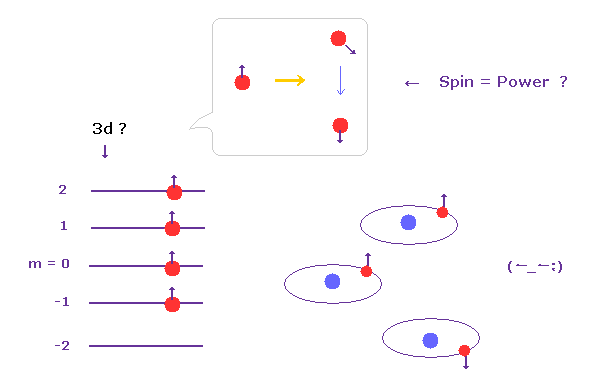
「スピンはめぐる」朝永著 によれば、スピン磁気モーメント間の相互作用は 恐ろしく弱い (= 微細構造レベル 0.00005 eV )。
つまり 様々なクーロン相互作用に打ち勝って この弱い "スピン" が いろんなマクロ現象を引き起こす主導的な立場を取ることは 絶対に不可能と言っていい。
それにも関わらず 彼らは この非常に弱いスピンに 強力な "リーダーシップ" を与えようとしている。なぜか?
その主要な要因は すでに述べたように 不思議な "パウリの排他原理" が すべての基本的な力の中で 最も強い効果を発揮するからである。
また 物性物理学においては 様々な 人為的なルールが好きである。
L-S カップリングにおいては、電子が 少ししかないときは 全角運動量は J = L-S となるが、 ある時点からは 突然 J が L+S になると 彼らは主張している ( 非常に "便利な" スピン である )。
もちろん、これらの数学上の原子軌道や ( 回転する ) スピン自体を 直接確認することは 不可能なため まったくの憶測にすぎない。
(Fig.7) 本当のスピン ? 点状粒子が ?
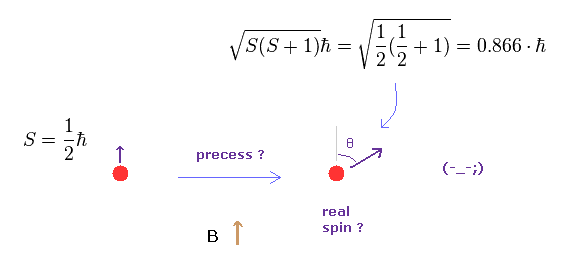
人為的なルールに加えて なんと この"スピン"は 歳差運動していると 彼らは主張している。
つまり 量子力学によれば、"本当の" スピン角運動量は 1/2 ħ では ない ということになる。
それに どうやって 点状粒子のスピンが 歳差運動できるのだろうか?
また どうして この歳差運動の傾き角度 (= θ ) が 様々な異なった磁場の下でも 常に決まった値になるのだろうか?
非常に奇妙である。
(Fig.8) ”数学上”の フォノン = 粘性 ??
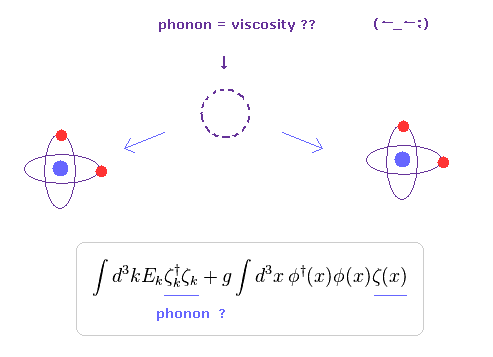
超流動は 極低温で 物質中の 粘性がゼロになる現象である。
問題は 現在の量子論では この現象を 単なる"数学上"の フォノン を用いて表そうとしていることである。
(Eq.1) 対称性の破れ ?
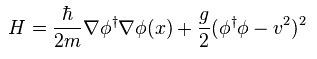
現在の量子論によれば 非相対論場における ヒッグスポテンシャルは Eq.1 のように与えられる。
(Eq.2)
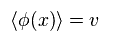
φ が "v" に決まると (= Eq.2 )、これは基底状態であり、 "対称性" が 破れた と 彼らは主張している。
(Eq.3)
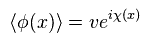
また Eq.3 のように
彼らは 非常に抽象的な概念である "位相" なるものを導入することが好きである。
( しかし 彼らは 決して この位相とは 何なのか 説明しようとしない。 )
この 位相 χ(x) が 位置変数 "x" を含んでいるとき、 Eq.1 のエネルギーは 基底状態よりも高くなる。
(Eq.4)
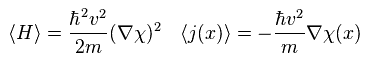
よって この位相 χ(x) における 非均一性が 超流動を引き起こすと 彼らは主張しているのである。
しかし ほとんどの人々が感じられるように、これらの抽象的な数学上の記号のみで 様々な ダイナミックな現象を記述することは 不可能と言っていい。
簡潔に言えば、これらの理論は 数学上の拘束のために より現実的で有用な方法を試せないのである。
(Eq.5)
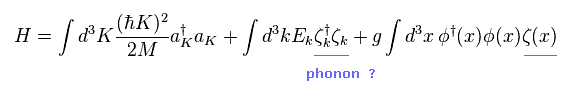
また 彼らは 突然 Eq.5 のように 架空の "フォノン" を含むハミルトニアンを導入した。
これらの 生成、消滅演算子 (= ζ ) は "フォノン" を表し、 魔法のように 超伝導などを引き起こすと 彼らは主張している。
最初の項は 電子のハミルトニアン (= 運動エネルギー ) で、2番目の項がフォノンのエネルギーである。
そして 3番目の項が 電子と "フォノン" 間の 相互作用ハミルトニアンである。
(Eq.6)
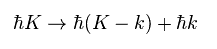
電子が 単一のフォノンよりも高いエネルギーを持つとき、それは フォノンを放出することができ それが 他の電子に 粘性を引き起こすと 彼らは主張している。
つまり 極低温で 各電子が 単一のフォノンよりも 低いエネルギーのとき、それらは相互作用できず、"超流動" になるということになる。
もちろん これらのフォノンが 非現実的な準粒子であることを考慮すれば、 彼らは 速やかに これらフォノンの正体が いったい何なのか 明らかにすべきである。
(Eq.7)

BCS 理論によれば、2つの 負電荷の電子が 互いに 引きつけられ、安定な クーパー対を生じるとしている。
再び 彼らは この不思議な引力の 具体的なメカニズムに関する説明を避けている。
Eq.7 の 第3項目の "g" が 正 のとき ( g > 0 )、スピンアップとダウンの電子が 引力相互作用によって クーパー対を形成すると 彼らは主張している。
(Eq.8)
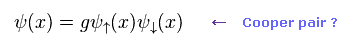
Eq.8 が クーパー対である。
しかし 21世紀にもなって これらの具体的なメカニズムは 不明のままである。
莫大な費用を 役に立たない加速器に浪費する前に このフォノンの正体を 真先に 明らかにするのが先であろうと思われる。
(Fig.9) 近藤効果は スピンの証明には まったくならない。
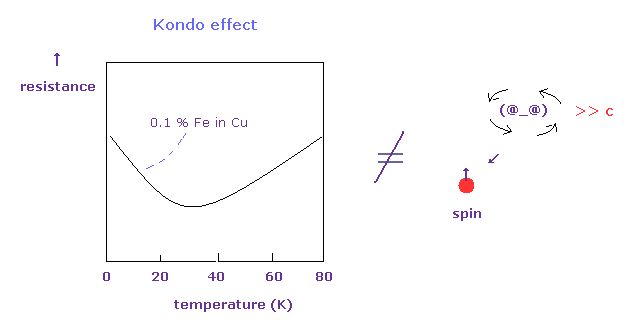
基本的に 温度が下がるにつれて、電子の抵抗は 弱くなっていく。
しかし 磁性体を少量 不純物として含む金属 ( ex. Cu + 0.1 % Fe ) では、この抵抗が さらに低温において 再び上昇する。
彼らは これらの効果が s と 3d 軌道の電子間の スピン・スピン相互作用によって生じるとしている。
しかし このセクションで説明するように、これらの理論は いわゆる "スピン" の 証明には まったく ならない。
つまり "スピン" とは 単なる 数学上の記号 にすぎず 物理的実態がないということを示す。
(Eq.9) アンダーソン ハミルトニアン。
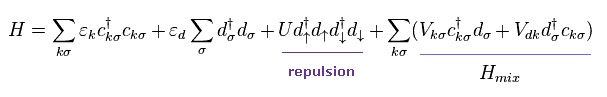
Eq.9 では c† と c は 伝導電子 (= s 軌道 ) の 生成消滅演算子を意味している。
また d† と d は Fe などの 磁性不純物の 3d 軌道の電子を表している。
( Fig.3 で述べたとおり、これらの非常に抽象的な演算子が より ダイナミックな 電子の振る舞いを表現することは 不可能である。 )
第1、第2項が 各電子の独立したエネルギー、第3項が
3d 電子における 反発クーロン相互作用である。
また 4項目が s (= c ) と 3d 電子間の 相互作用ハミルトニアンである と彼らは主張している。
(Eq.10)
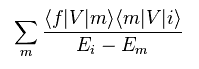
このページに示したように、2次の 有効ハミルトニアン ( "V" に対する ) は Eq.10 のようになる。
"f"、 "m"、 "i" は "最終", "中間"、 "最初" の状態の意味である。
(Fig.10) 伝導電子が 3d 電子によって k' 状態へ 散乱される。
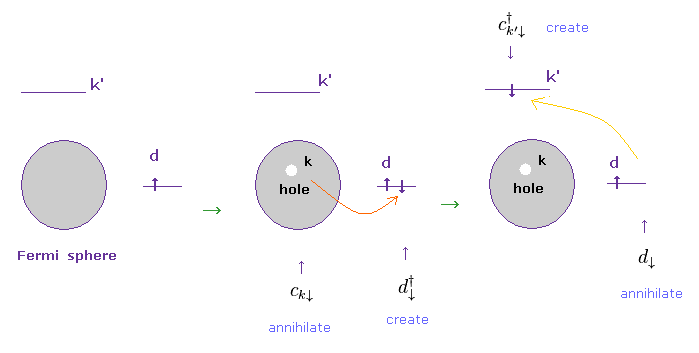
Fig.10 は ある伝導電子が そのフェルミエネルギー状態から 3d 軌道、そして 他の伝導状態 (= k' ) に移る過程を表したものである。
残念ながら Eq.11 に示したように 彼らは これらの物理現象を 非常に抽象的な 生成消滅演算子のみを 用いてしか表現できない。
(Eq.11)
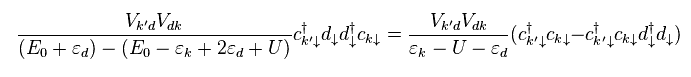
伝導電子が フェルミ球で 最初に消滅し (= c )、それから 3d 軌道で生成される (= d† )。
その後、この電子は 消滅し (= d )、 k' 状態に移動する (= 生成、 c† )。
分子では Eq.9 の 相互作用ハミルトニアン V のみが関わっている。
2つの電子が 3d 軌道に存在しているとき、反発相互作用 (= "U" ) が 現れる。
もちろん 3d 軌道の 2つの電子は パウリの排他原理を満たす。
( しかし これらの状態は 直接見ることはできず 単なる想像上の産物にすぎない。 )
(Eq.12)
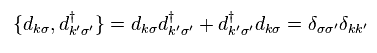
Eq.11 では、Eq.12 の 反交換関係が使用されている。
上で述べたとおり、この反交換関係 (= パウリの排他原理 ) は いかなる状況においても 絶対的な力を持つのである。
スピン磁気モーメント自体が 非常に 弱いにも関わらずだ。
(Eq.13)
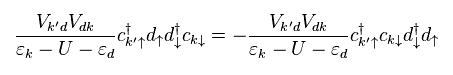
Eq.13 では、 最後の k' の電子が "up" スピンを持つ ( Eq.11 の "down" スピンの代わりに )。
このように この過程では 全部で 8つもの異なるパターンが存在する。
すべての散乱パターンを足して、次の s-d 模型のハミルトニアンを得る。
(Eq.14)
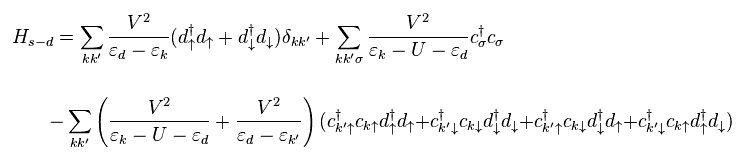
Eq.14 では、様々な 相互作用 Vkd を 1つの共通の "V" に近似的に変えてしまった。
しかし もっとも重要な部分は この相互作用 V の多様性である。
彼らが 電子の より具体的 かつ 動的な 動きを調べようとしない限り、現在の量子論は 行き詰った袋小路から
決して 脱出することができない。
(Fig.11) "スピン" = 数式 ?? 何の物理的実態がない。
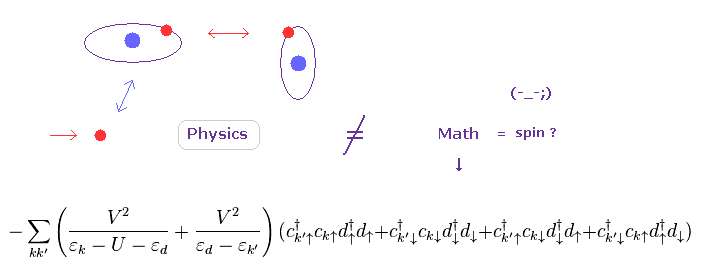
結論からして 物性物理学や スピントロニクスの分野の 様々な論文に現れる "スピン" というものは 単なる"数学的記号" にすぎず、何の 物理的実態がない と言える。
彼らが より多様性に富む ダイナミックな 散乱などを表現したいときは、もっとリアル かつ 具体的な模型を使用すべきである。
( スピノル行列や 演算子は あまりにも抽象的すぎる。)
(Eq.15)
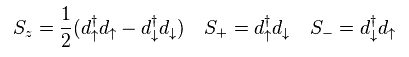
彼らは 3d 電子の演算子を スピン演算子 "S" に置き換えた。
このように 彼らは ほぼ盲目的に 単なる "数式記号" である スピン を信じ込んでいるといっていい。.
たから "スピン" という語句は 物性物理系の論文には 必ずと言っていいほど 出現する。
スピン とは いったい何なのかと 問おうとはしないのに。
(Eq.16)
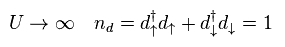
ここでは 彼らは 反発クーロンエネルギー U を 無限大と定義した。
よって 3d 電子の最終の総数は "1" になる ( "2" ではなく )。
Eq.15 と Eq.16 を用いて、
(Eq.17)
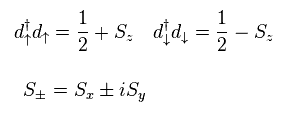
彼らは 伝導電子のエネルギーが 反発エネルギー U よりも かなり小さいと仮定した。
また Eq.18 のような "粒子ホール対称性" といった特殊なエネルギー関係式を定義した。
(Eq.18)
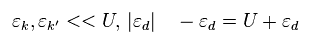
ここでは 次のパウリ行列を用いる。
(Eq.19)
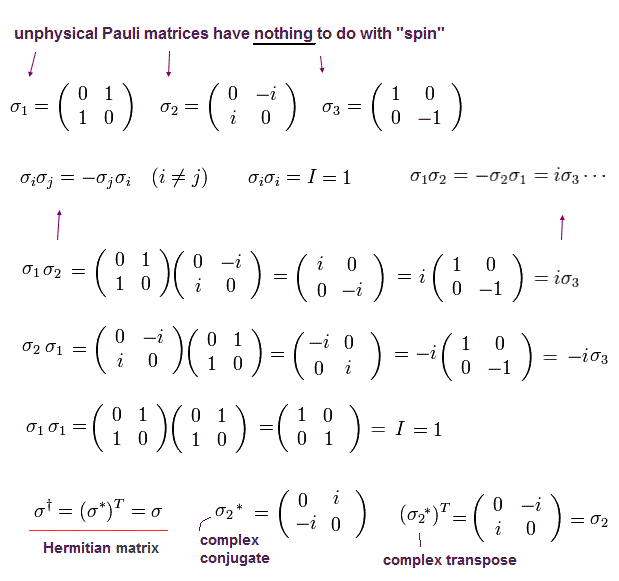
重要な点は パウリ行列の "x" (= 1 ) と "y" (= 2 ) 成分は 量子力学自身とも 矛盾するということである。
なぜなら ステルン・ゲルラッハによれば スピンには "z" 方向に "up" と "down" の2方向しかないはずだからである。
パウリ行列を用いて、伝導電子の演算子を次のように変える。
(Eq.20)
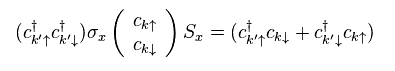
結果的に Eq.14 の s-d ハミルトニアンは、
(Eq.21)
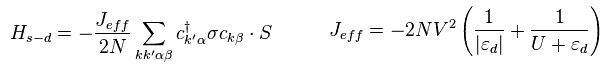
Eq.21 では、 Jeff は 負であるため、 s (= σ ) と d (= S ) の電子は 互いに反平行であるとき、
(Eq.22)
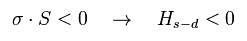
ハミルトニアン (= Hs-d ) は 負で 安定になる (= 近藤1重項 )。
そのため 彼らは 伝導、3d 電子が 反磁性の関係にあると主張している。
もちろん、スピン磁気モーメント自体に 様々なクーロン力に打ち勝つだけの 力は ない。
つまり Eq.22 の関係式は 完全に 非実在的なもの と言える。
実際に 彼らは "スピン" の具体的な姿かたちを まったく示そうとせず、ただ数式のみを示すだけである。
残念ながら これが スピントロニクスにおける "スピン" の 実態 である。
(Eq.23)
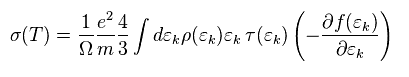
電気伝導率 (= σ(T) ) は J = σ(T) E と定義される。
( J = 電流、 E = 外電場。 )
このセクションでは、この伝導率が Eq.23 のように表されることを示す。
Eq.23 では、 τ は 緩和時間 である。
この τ の時間経過後、電子状態は ほぼ 元の状態に戻るとする。
"f(ε)" は 電子の分布 (= フェルミ・ディラック 統計 ) である。
(Eq.24)
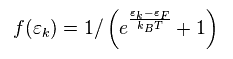
電流 J を Eq.25 のように定義する。
"ħk" は 運動量 "p"、 Ω は 抵抗である。
(Eq.25)
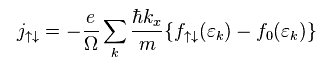
" f↑↓ " と " f0 " は それぞれ 電流があるとき と ないとき の フェルミ分布を 表している。
彼らは 緩和時間 τ の後、 "f↑↓" が 静的な "f0" の戻ると仮定している。
f↑↓ の "t" に関する導関数は、
(Eq.26)
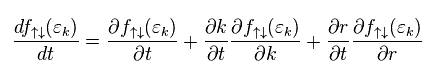
ここで 電流 (= 状態 ) を ほぼ一定と近似する。
(Eq.27)
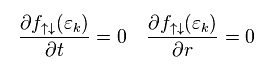
ニュートンの法則によれば、
(Eq.28)
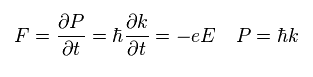
Eq.26 - Eq.28 から、 τ の時間経過中の "f(ε)" は、
(Eq.29)
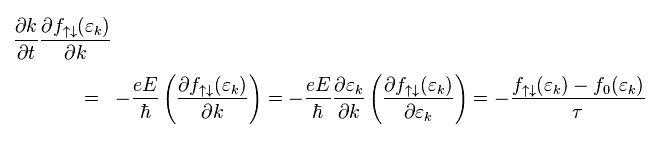
ここでは
(Eq.30)
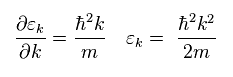
Eq.25、 Eq.29、 Eq.30 から、 電流 j は、
(Eq.31)
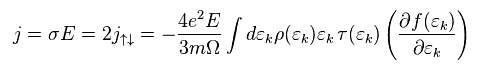
ここでは
(Eq.32)
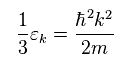
Eq.31 では、 彼らは Σ (= "運動量" の合計 ) を 確率密度 ρ を用いて ε の積分に変えた。
結果的に Eq.23 で 伝導率 σ を得ることができた。
遷移確率は フェルミの黄金律 を用いて 次のように表せる。
(Eq.33)
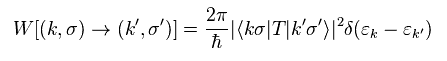
摂動理論によれば、遷移行列 "T" が 次のように定義される。
(Eq.34)
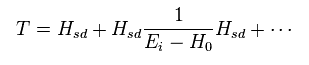
最初に Hsd ( "V" でなく ) に関して 1次の摂動を考える (= Eq.34 右 の最初の項 )。
スピン演算子は 次を満たす。
(Eq.35)
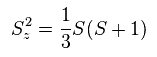
また 緩和時間 τ は 次のように定義される。
(Eq.36)
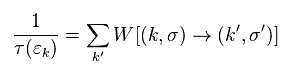
Eq.21、 Eq.33-Eq.36 から
(Eq.37)
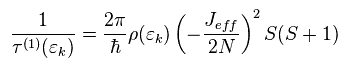
Eq.37 の結果は 1次の摂動 (= ボルン近似 ) である。 ここには 温度 "T" が含まれていないため、温度依存の抵抗を表せない。
Eq.34 右の2項目に示すように、2次のハミルトニアンは ( E-H ) の逆数 を含む。
量子力学における この数学的な定義が 近藤効果における 深刻な 無限大への 発散につながる。
(Eq.38)
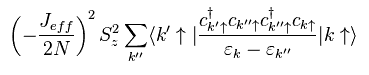
Eq.34 右の 2項目は 2つの Hsd を含むため、演算子の数は 2倍になる。
そのため 伝導電子は あちこちに より多く散乱されることになる。
よって 2次の摂動では より多くの散乱パターンを考慮する必要がある。
(Fig.12) 高次 = 相互作用弱い のに 散乱 ↑↑ ?
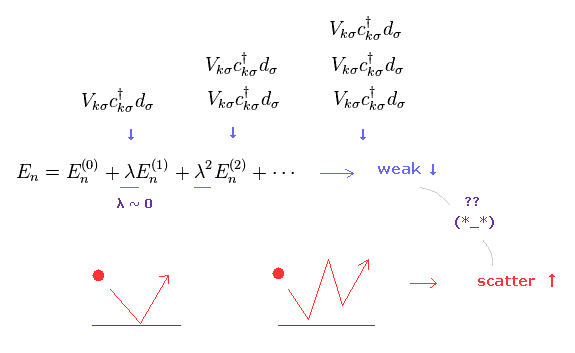
奇妙なことに、これらの摂動方法では より高次の相互作用になればなるほど、 より多く散乱されることになる。
この相互作用は おかしいと言わざるを得ない。
なぜなら より高次の相互作用は小さい λ のために より弱くなるはずだからである。
つまり 具体的な説明を示せないだけでなく、この方法は 自己矛盾を含むことになる。
(Eq.39)
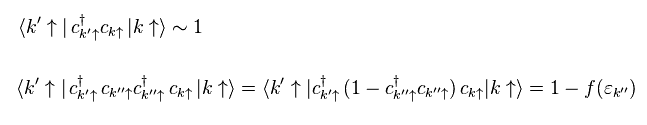
Ee.39 のように、反交換関係を用いる。
c†c は 数演算子 (= f(ε) ) である。
すべてのパターンを足すと、 Eq.38 は 次の式を含む。
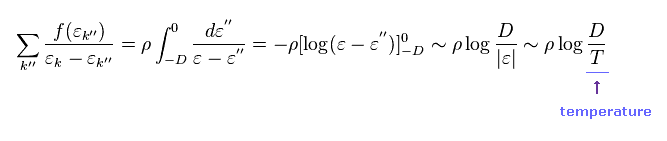
Eq.40 では、 Σ が 積分に変えられた。
結果的に Hsd に関する 2次の摂動は 温度 (= T ) を与えることができた。
電気伝導率は
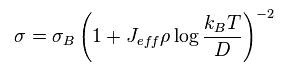
そのため 電気抵抗は
(Eq.42)
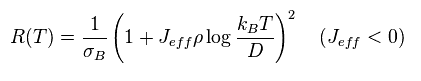
Eq.42 に示すように、温度が低くなるにつれて、抵抗が強くなる (= 近藤効果 )。
問題は この温度 T が 0 (K) に等しいとき、この抵抗が 無限大に発散してしまうことである。
(Eq.43)
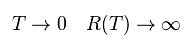
そのため 彼らは この深刻な問題を 組み込み などの 数学的トリックを用いて解決しようとしている。
しかし 量子力学の こういったユニタリー性の数学が 必ず 発散という深刻な問題 に繋がることは明白である。
ご存じのとおり、この量子力学の 最終形態 が 非現実的な 10次元の ひも理論 なのである。
これらの問題やら ボーア模型が 何の 発散やら特異点 などの深刻な数学上の問題を 抱えていないことを考慮すれば、奇妙な量子力学より より妥当な模型と言える。
極低温においては 不純物による ドブロイ波効果が 非常に 優勢になるため 伝導電子の抵抗を引き起こすと 考えるのが自然である。
つまり 近藤効果は 磁束量子や強磁性体のように ドブロイ波で説明可能なのである。

2013/9/17 updated This site is link free.