トップページ (2電子原子も含む正確な新ボーア模型)
プランク定数の本当の意味とは
量子ホール効果は 低温と強磁場のもとでの 2次元電子系で観察される現象である。
この状態で ホール伝導率 σ は 量子化された値をとる。(= n e2/h )
ここには プランク定数が含まれているため、プランク定数の決定に使用される。
また、量子ホール効果は 電気抵抗 の標準的な基準値として重要である。
ところで、この量子ホール効果とは 一体全体何なのだろうか?
また、この効果の プランク定数 h は 実際 何を意味しているのだろうか?
このページでは、量子ホール効果の 具体的なイメージと本当の意味を探究することにする。
量子ホール効果では 電子の運動範囲が 1平面のみに限定された 2次元電子系が使われる。
この条件をつくるには、半導体と他の物質の間の境界面を利用する。
半導体は 導体と 絶縁体の中間の性質を持ち、また とびとびの バンドエネルギー準位を持つ。
バンド準位の間隔は 絶縁体と比べて 狭いため、導体としてもふるまうことが可能である。
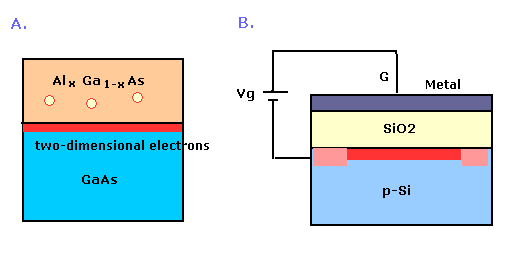
(Fig.1)

Fig.1 の A は III-V族化合物半導体である GaAs / Alx Ga1-x As のヘテロ界面である。
上層の AlGaAs は ドナーから 下層に電子を供給する。
これらの電子は クーロン力によってまた上層に引き戻されようとするため、結果として これらの2層の境界面にトラップされる。(赤い部分)
Fig.1 の B は metal-oxide-semiconductor (MOS) 構造である。
MOS 装置は 適度に不純物を施した p-タイプ (青) もしくは n-タイプ (ピンク) のシリコンから成る。
2次元電子系 (赤い部分) の上には、 酸化シリコンと金属の層が存在する。
これらの垂直方向のエネルギー準位は とびとびのため、運動する電子は 赤い層に閉じ込められる。
Vg は "ゲート電圧" と呼ばれるものでる。
Vg が大きくなるにつれて、より多くの電子が赤の層に入っていき、電流(伝導率)が増加する。
最初に、量子力学的な方法で 単位面積あたりの電子数を計算する。
x-y 平面の 電子のシュレディンガー方程式は、
(Eq.1)
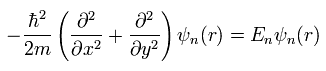
ここでは 1辺の長さ L の正方形 に電子が閉じ込められていると仮定する。
周期的境界条件は
(Eq.2)
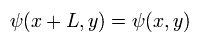
波数ベクトル (k) を使って、波動関数 (ψ) は次のように表せる。
(Eq.3)
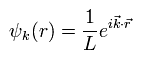
Eq.2 から 波数の x と y 成分は
(Eq.4)
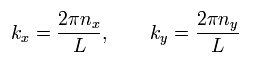
ここで nx と ny は 整数である。
これはつまり 波長 (λ) が量子化されていることを意味している
ド・ブロイの関係から、電子の運動エネルギーは
(Eq.5)
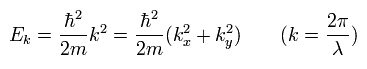
フェルミエネルギー (EF) は フェルミ波数 kF を使って次のように書ける。
(Eq.6)
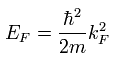
半導体もしくは絶縁体においては バンド構造が形成され、電子が 順番に低いエネルギー準位から配置されていく。
電子を収容する最も高いエネルギー準位を "フェルミエネルギー"という。
(注意: 量子力学的な世界は 数学的な性質が強いため 具体的に思い浮かべるのは困難である。)
2次元波動空間の体積要素は (2π / L)2 である。
フェルミ円 (πkF2) の中に許される状態数は
(Eq.7)
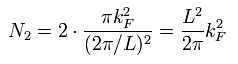
ここでは スピンの自由度 (= 2 ) を使っている。
Eq.7 から、単位面積あたりの電子数は
(Eq.8)
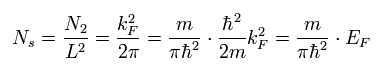
(注意; この結果は 最初から L=1 と仮定しても変化しない。 )
しかし、実際は Eq.8 の "数学的な"結果は 現実の世界とは少し違う。
Eq.7 と Eq.8 による 電子の数密度は 各波数における 実際の面積の違いを考慮していない。
ローレンツ力によれば、エネルギー準位が高くなるにつれて ランダウ軌道半径は大きくなる。
つまり、我々は 電子の密度を導出するとき、状態数に加えて "実際の面積"について考える必要がある。
次に 電磁場のもとでの 電子の運動について考える。
電子が x-y 平面上を運動していて、磁場 (B) が z 方向を向いているとする。
(Fig.2)
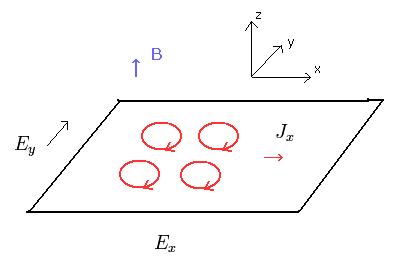
ローレンツ力とクーロン力から、運動方程式は
(Eq.9)
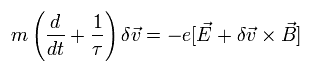
ここで δv は 波動関数空間における 電子の速度を意味している。
(量子力学的には ちょっと想像しがたいが、古典力学的には 簡単な原理である。)
m, E, B は それぞれ 電子質量、電場、磁束密度を意味している。
Eq.9 の 左辺の τ は 散乱の緩和時間を意味している、
τ が長くなるにつれて、電子が他の物質によって 散乱されにくくなる。
(τ が 長くなるにつれて、散乱による”摩擦”は小さくなる。)
磁場 (B) が z 方向を向いている (0, 0, +B) として、電子の運動の x と y 成分は
(Eq.10)
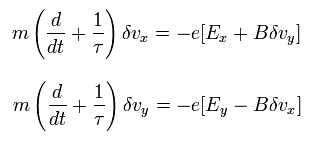
定常状態では δv の時間微分は 次のようにゼロになる。
(Eq.11)
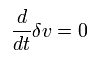
磁場のもとでは 電子は 円運動する。
遠心力が ローレンツ力 に等しいとすると, 角振動数 (ω) は、
(Eq.12)
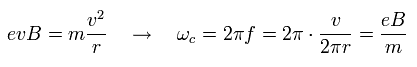
Eq.11 と Eq.12 から Eq.10 は
(Eq.13)
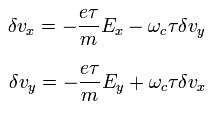
Eq.13 を解くと、速度の x、 y 成分は
(Eq.14)
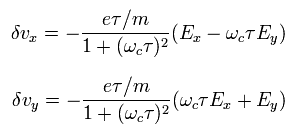
ここで σ0 を次のように定義する。
(Eq.15)
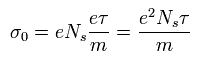
ここで Ns は 単位面積あたりの電子の数を意味している。
Eq.14 と Eq.15 を使って、電流密度 ( J = -eNsv ) は、
(Eq.16)
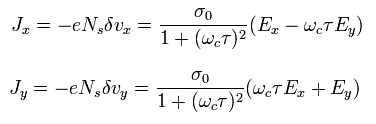
Eq.16 は 電気の伝導率テンソルを使って 次のように表せる。
(Eq.17)
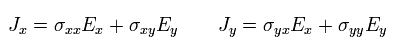
電気伝導率が大きくなるにつれて、より多くの電子が流れるようになる。
Eq.16 と Eq.17 より、
(Eq.18)
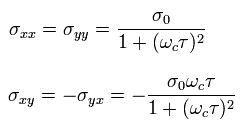
Eq.18 の σxy は 次のように変えられる。
(Eq.19)
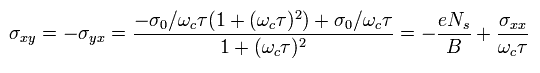
逆行列を使って、Eq.17 は次のように表せる。
(Eq.20)
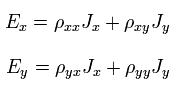
ここで ρ は 電気の抵抗率 を意味している。(ρ = R = 抵抗。)
逆行列の公式より、各 ρ は
(Eq.21)
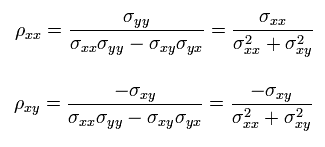
Eq.12, Eq.15, Eq.18, Eq.21 より、
(Eq.22)
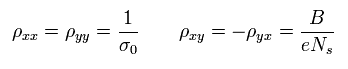
強磁場のもとでは、2次元の系の電子は ローレンツ力によって円運動する。
(サイクロトロン運動。)
このサイクロトロン運動の角振動数は Eq.12 である。
量子力学的な調和振動子によれば、この電子のエネルギーは 次のように 量子化される。
(Eq.23)
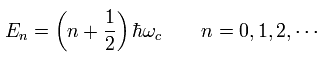
Eq.23 は "ランダウ準位" といい、 n は "ランダウ指数"という。
また、ランダウ軌道半径は
(Eq.24)
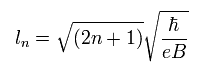
お気づきのとおり、これらの方法は 古典力学と量子力学的な概念の両方を含んでいる。
そのため、イメージするのが難しい。
Eq.8 のスピンの効果を忘れて、ゼロから n までの ランダウ準位に含まれる 状態数は
(Eq.25)
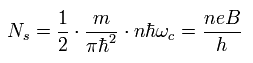
また、これもイメージが難しい。
(もし 電子が ゼロから n のエネルギー準位にあるのなら、どうして n だけでなく 1+2+3+ ... n にしないのだろうか?)
次に これらの運動の具体的な状態を説明する。
電子は z 方向の磁場 B のもとで、x-y 平面上を ローレンツ力によって 動き回っている。
(Fig.3)
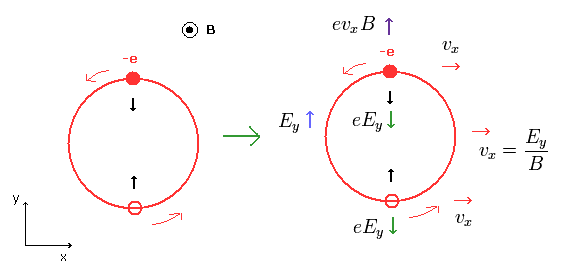
y 方向の電場が与えたれたとき ( Ey )、電子の円全体は Fig.3のように x 方向 に進む。
電子が x 方向にすすんでいるときの この運動による ローレンツ力は 次のように 電場に等しくなる。
(Eq.26)
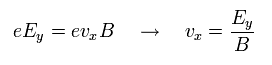
Eq.26 から、x方向への 電流密度は
(Eq.27)
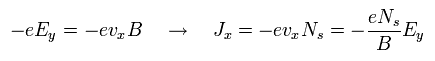
ここで Ns は 数密度である。
Eq.17, Eq.25, Eq.27 より、ホール伝導率 ( σxy ) は、
(Eq.28)
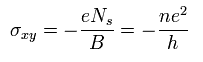
結果として、ホール伝導率は 量子化された。
Eq.28 の n は "ランダウ準位充填率" と呼ぶ。
また h/e2 は von Klitzing 定数 Rk (Ω) である。
Eq.27 と Eq.28 が満たされるとき、摩擦はゼロになる。
(散乱の緩和時間 τ は無限大になる。Eq.19 も参照のこと。)
ところで、電場 Ey による y 方向の電流はどのように生じるのだろうか?
磁場のもとでの この電流は Fig.4 に示すように 電子の 散乱によって生じる。
(Fig.4)
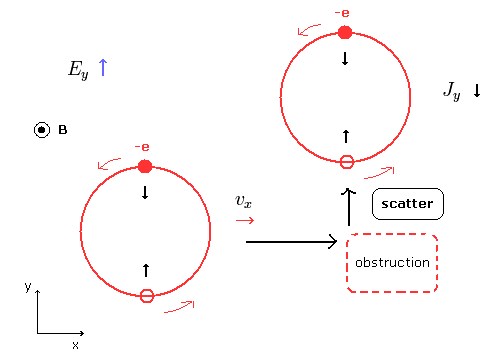
Eq.15, Eq.18, Eq.22 に示すように、緩和時間 τ が長くなるにつれて、対角抵抗率 (ρxx) と 対角伝導率 (σxx) は小さくなっていく。
(Eq.29)
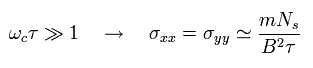
(Eq.30)
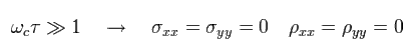
これは 対角伝導率は 電子の散乱に関係していることを意味している。
そのため、対角抵抗率 (ρxx) が ゼロでないとき、ホール伝導率 σxy (もしくは ホール抵抗率 ρxy) は 量子化されない。
しかし、後の研究により、Eq.28 の n は 整数だけでなく 分数も含んでいることが分かった。
これはつまり ランダウ準位充填率を用いた 上の仮説は 不完全であることを意味している。
我々には 別の説明が必要なのである。
(分数は 電子間相互作用によって生じるとされているが、そのメカニズムはよくわかっていない。)
2次元電子系において、ボゾンでもフェルミ粒子でもない "エニオン (anyon)" という奇妙な概念を導入しようとしている研究者達がいる。
エニオンは "分数電荷 (= 1/m e)" を持つ。しかし はたしてこんな奇妙なものが存在しているのだろうか?
かわりに、ここでは ボーアのド・ブロイ波を用いて 分数量子ホール効果を 自然に説明することを試みる。
電子軌道が ド・ブロイ波の整数倍 という ボーア・ゾンマーフェルトの量子化条件を使う。
つまり 次の2つの条件が満たされている必要がある。
(Eq.31)
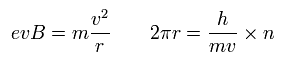
最初の式は 遠心力とローレンツ力の釣り合いである。
Eq.31 を解くと、次を得る。
(Eq.32)
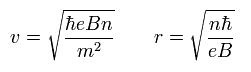
Eq.32 より 円の面積は
(Eq.33)
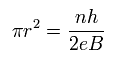
電子の運動エネルギーは、
(Eq.34)
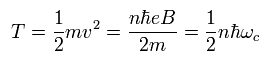
ここでは 次の Eq.12 を使っている。
(Eq.12)
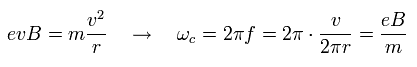
運動エネルギーに加えて、現実の世界では 磁気エネルギーを考慮しなければならない。
磁気モーメントは 次のように 電流 (I) × 面積で表される。
(Eq.35)
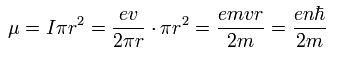
磁場 B のもとでの 磁気エネルギーは
(Eq.36)
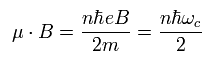
ここでは 磁気モーメントと 磁場の方向は逆であるため、その相互作用エネルギーは "正"になる。
Eq.34 と Eq.36 を足して、
(Eq.37)
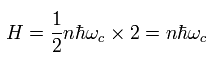
この結果は Eq.23 の ランダウエネルギー準位とほぼ等しい。
つまり、我々は ランダウエネルギー準位を "古典力学的な方法"(+ド・ブロイ波)で説明することができた。
ここでは Eq.33 の面積の軌道に k 個 の電子が含まれていると仮定する。
Eq.26 と Eq.33 を用いて、電場 Ey によって生じる x 方向の電流密度 (Jx) は、
(Eq.38)
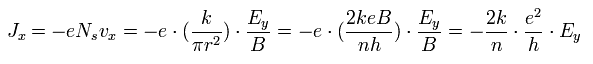
Eq.38 より、 ホール伝導率 σxy は、
(Eq.39)
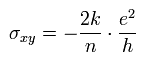
なんと Eq.39 は 分数量子ホール効果を表している!
(Eq.39 と Eq.28 を比較してみるといい。)
Eq.39 の分子の " 2 "の因子の影響で、Eq.39 を既約分数にしたとき その分母は "奇数" の値になりやすい。
また この場合では ホール抵抗 ρxy は、
(Eq.40)
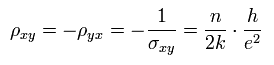
すでに述べたように、対角抵抗率は 電子の散乱に関係している。
そのため 対角抵抗率 (ρxx) がゼロのとき、ホール伝導率 σxy (もしくは ホール抵抗率 ρxy ) は量子化される (= 分数で)。
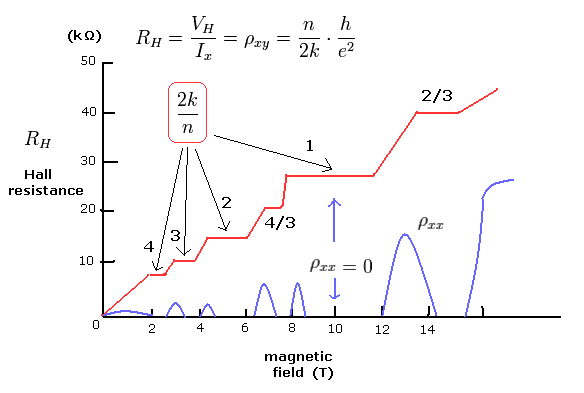
(Fig.5) 実験結果。
E と J に 長さ l をかけて、
(Eq.41)
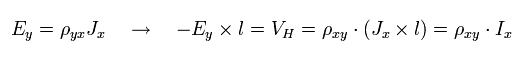
ここで VH と I はそれぞれ 電位と電流を表している。
ホール抵抗は 次のように ρxy と同じである。
(Eq.42)
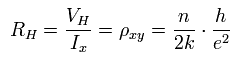
では Eq.39 の 各 2k/n の具体的な状態はいったい何なのだろうか?
Eq.39 では n は 軌道のド・ブロイ波の数、k は そこに含まれる 電子の数を意味している。
まず最初に 2k/n = 1 について考える。(Fig.5 も参照のこと。)
(この場合は Eq.28 の n=1 に相当し、"整数"量子ホール効果である。)
例えば、2 × ド・ブロイ波長 (n=2) の1軌道が 1つの電子を含んでいる (k=1)。 (Fig.6.)
(Fig.6) 2k/n = 1 の1例。
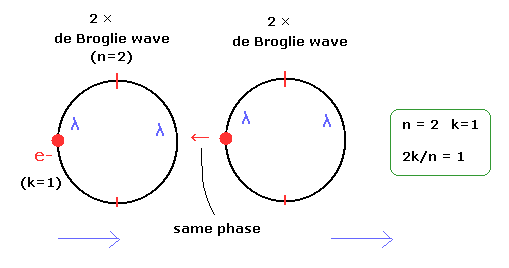
もし 1 × ド・ブロイ波長 の軌道のみ 平面に存在するとしたら、隣どうしの軌道の 逆の波の位相どうし打ち消しあってしまう。
つまり 電子の動きは不安定になり、散乱されると考えられる。
--------------------------------------------------
軌道長が 1 × ド・ブロイ波のとき、この電子の運動による 磁気モーメントは いわゆる "ボーア磁子"になる。
そして、このボーア磁子は スピン磁気モーメントと同じである。
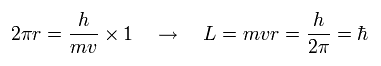
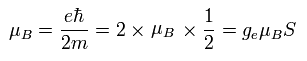
ローレンツ力は 磁場 (B) と逆方向の磁気モーメントを生じる。
安定した低いエネルギー準位になるには、その磁気モーメントの方向が 磁場と同じになる必要がある。
そのため ボーア磁子の方向は "振動している" と考えられる。
-----------------------------------------------------
Fig.6 の場合は、隣あう 2 × ド・ブロイ波長の軌道の 同位相の波は 互いに干渉して くっつきあうことができる。
次に 2k/n = 2 の場合を考える。
(この場合は Eq.28 の n=2 に相当する。)
例えば、2 × ド・ブロイ波長 (n=2) の軌道が 1つの電子を持っているとする。
さらに 1つの電子を含んだ 1 × ド・ブロイ波長の軌道が その中に含まれているとする。(Fig.7)
(結果として、k= 1+1 = 2 となる。)
(Fig.7) 2k/n = 2 の1例。
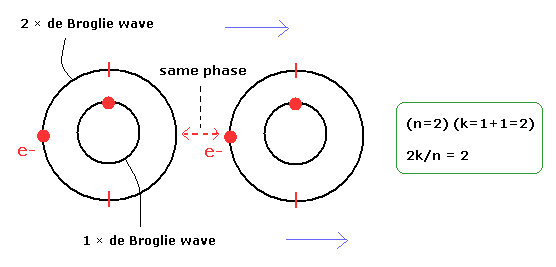
Eq.26 によれば、これらの軌道の x方向の速度は同じである。
次に 2k/n = 3 の場合を考える。
(このケースは Eq.28 の n=3 に相当する。)
例えば、4 × ド・ブロイ波長 (n=4) の軌道が 2つの電子を含むとする。
さらに 2電子を持つ 3 × ド・ブロイ波長の軌道と 2電子を持つ 2 × ド・ブロイ波長の軌道がその中に含まれているとする。(Fig.8)
(結果として、k = 2 + 2 + 2 = 6 となる。)
(Fig.8) 2k/n = 3 の1例。
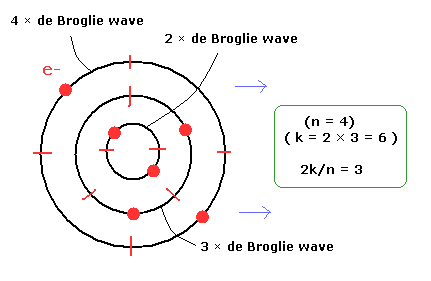
Eq.26 によれば これらの軌道の x方向の速度は同じである。
Fig.5 に示されるように、2k/n = 3 の場合の磁場は 1 や 2 の場合のときより 弱い。
磁場が 弱くなるにつれて、Eq.32 の 軌道半径は大きくなる。
そのため 電子間の反発力は弱くなり、いくつかの異なる軌道が 重なることが可能になる。
次に 2k/n = 4/3 について考える。
(このケースは Eq.28 の n = 4/3 に相当する。つまり 分数量子ホール効果である。)
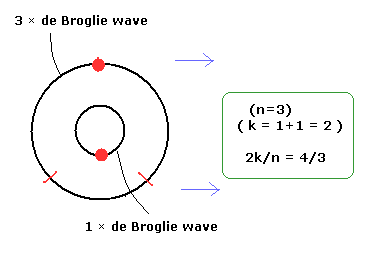
例えば、3 × ド・ブロイ波長の軌道 (n=3) が 1つの電子を持つとする。
さらに 1つの電子を持つ 1 × ド・ブロイ波長の軌道がその中に含まれるとする。(Fig.9)
(結果として、k = 1+1 = 2 となる。)
(Fig.9) 2k/n = 4/3 の1例。
次に 2k/n = 2/3 を考える。
(このケースは Eq.28 の n = 2/3 に相当する。つまり 分数量子ホール効果である。)
例えば、3 × ド・ブロイ波長 (n=3) の軌道が 1つの電子を持つとする。
(結果として、k=1 となる。)
(Fig.10) 2k/n = 2/3 の1例。
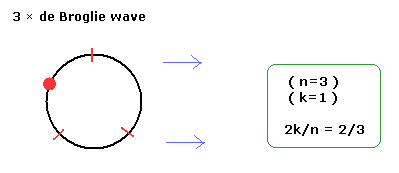
Eq.32 に示すように 磁場(B) が強くなるにつれて、軌道長は小さくっていく。
そのため Fig.10 の半径は 同じ n=3 の軌道でも Fig.9 に比べて小さくなる。
よって Fig.10 では、電子間の反発力は強くなる。
結果として 小さい n=1 や n=2 の軌道が電子を含むことが より難しくなる。
これらのメカニズムにより、磁場が強くなるにつれて ホール抵抗が大きくなっていくことが説明可能となる。

2011/6/28 updated This site is link free.