Top page (correct Bohr model including helium)
Schrodinger equation is equal to Sommerfeld model.
Derivation of Riemann, Ricci, Einstein tensors.
Schwarzschild solution and GPS time correction.
Special relativity breaks down in electromagnetism !
First we review extremely close relationship between theory of relativity and quantum mechanics.
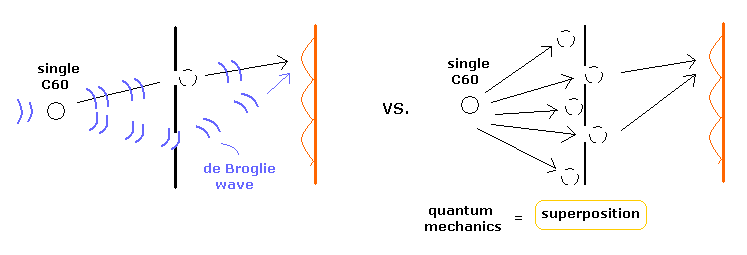
(Fig.1) A single C60 buckyball interferes with itself !

Relativity denied "ether", and introduced the new idea that time and space can change to keep light maximum speed c.
So we can NOT use "real" de Broglie waves as wavefunctions for electrons, because "real" de Broglie waves means "ether", as shown on this page (= Fig.1 left ).
And faster - than - light ( or many-world like ) collapsed wavefunction in quantum mechanics lacks reality.
Fig.1 right quantum mechanics shows the mysterious many-world like superposition of a single C60 molecule in the double slit.
This means unrealistic quantum mechanical interpretation supports the theory of relativity, which denied ether.
(Fig.2) Space is filled with many kinds of particles according to the relativity.
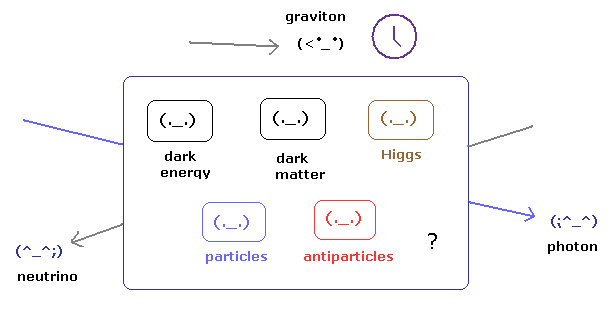
Basically in this real world ( NOT fantasy world ), there is only one space.
As you know, special relativity denied "ether" in the vacuum, so the vacuum must NOT contain anything.
But according to the present relativistic quantum field theory, the vacuum is filled with many kinds of particles (or matter ) such as dark energy, dark matter, Higgs particles, infinite pairs of particles and aniparticles !
Furthermore, photons and neutrinos have the special ability to go through this very crowded space "uninjured".
And gravitons cause not only force but also time dilation.
It is impossible that space contains those infinite particles, which do not influence photons and neutrinos, I think.
(Fig.E-1) "Division" of one electric wire into two ??
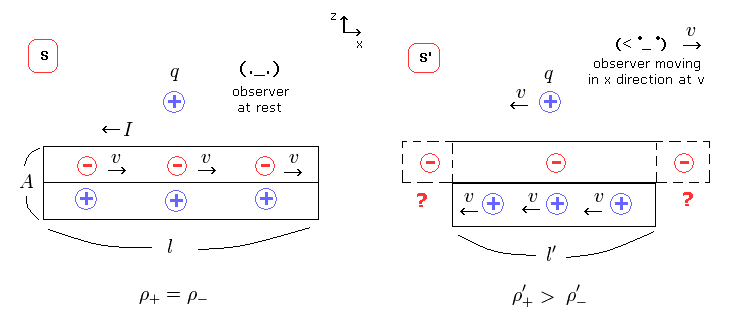
As shown on this page, the charge and current density of relativity generates strange charges from neutral current only by observer's movement, who doesn't touch the wire.
For example, from the viewpoint of s frame of Fig.E-1, when someone at rest cuts the both (definite) ends of the electric wire at some point, the same number of minus and plus charges are found in that wire.
But from the viewpoint of s' frame ( right of Fig.E-1 ), when someone at rest cuts the same both ends of the electric wire, there are more plus charges there !
This means Lorentz transformation itself is wrong.
(Fig.E-2) Twin paradox in the two identical satellites.
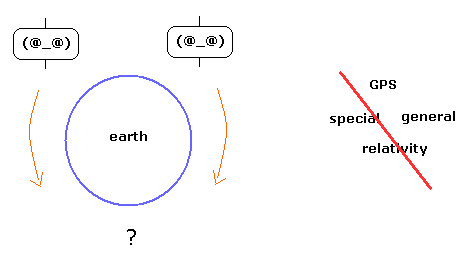
According to the special relativity, the Lorentz invariant proper time shows the clock accompanying the moving object.
From the viewpoint of one observer (= A ), another observer's (= B ) proper time is always delayed.
But from the viewpoint of the observer B, the proper time of A is always delayed.
This is called famous "twin paradox".
As shown on this page, when the two identical satellites are moving in the opposite directions on the same orbit around the earth, their proper times clealy show paradox.
( We can prove these are clearly twin paradoxes using general relativity including the centrifugal potential. )
So famous GPS satellite relativistic corrections which use special relativity include twin paradox.

The most important thing is that Schrodinger himself, who is great man in quantum mechanics, did not approve "probability concept" in wavefunction.
So he criticized the quantum mechanics using famous Schrodinger's cat.
Schrodinger, Einstein, and de Broglie were realists.
Einstein did not agree with the quantum mechanics throughout his life.
( See The Trouble with Physics, Lee Smolin. )
And Dirac, who is also a great figure in quantum theory, criticized the divergence of quantum electrodynamics.
Surprizingly, later he tried to revive "ether". ( See The Strangest Man, Graham Farmelo. )
Feynman disliked the string theory, which is 10 dimensions.
So the present quantum theory did NOT get the approval of the great figures of physics.
This is very important.
As you know, the electromagnetic forces such as Coulomb force and Lorentz force play a key role in our world.
General relativity was introduced to explain gravity.
What is the difference between gravity and the electromagnetic force ??
(Fig.3) There are NO gravitational "electromagnetic" forces.
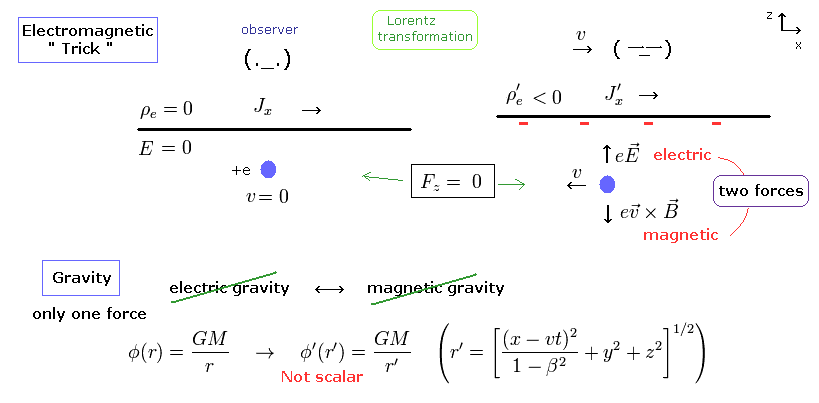
According to the special relativity, every physical phenomenon in the world looks the same in any inertial reference frame.
This means that even when the observer is moving at the different velocity, the object's reaction looks the same.
In the electromagnetic forces, there are two kinds of forces such as Coulomb force (= electric force ) and Lorentz force (= magnetic force ).
So combining these two different forces cleverly, the electromagnetism was incorporated into the special relativity successfully.
But in the gravity, there is only one kind of force.
So the gravity could not use this trick.
And from the different inertial frame ( under Lorentz transformation ), gravitational relation ( GM/r ) changes, as shown in Fig.3 ( = not scalar).
So the gravitational equation looks different from the moving observer.
To avoid this serious state ( in "mathematical" condition ), the gravity needs to be erased ( cancelled ) to match the special relativity.
This is called ( gravitational erased ) local inertial frame.
(Fig.4) Observer can erase gravity without touching the object ??
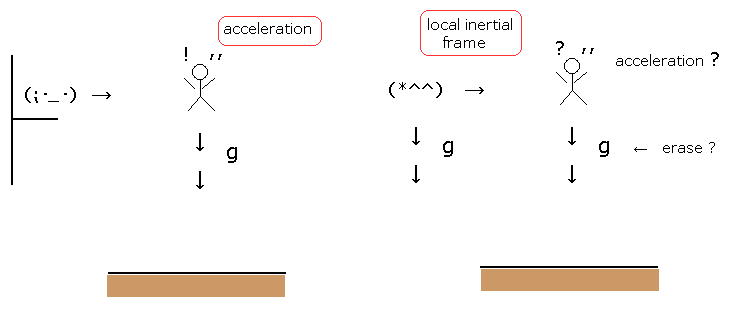
Suppose that one person is falling into the ground by the gravity.
Of course, from the observer at rest (= left of Fig,4), the person of object is being influenced by gravity.
But according to the general relativity, from the observer falling by gravity, the person of object is NOT influenced by gravity ! (= right of Fig.4 )
So in this state , we can use what we call Minkowski spacetime (= Lorentz invariant inertial frame ). This is called equivalence principle.
But is it really so ??
In spite of the observer who doesn't touch the object, the person who is falling by the gravity feels gravity. ( It is quite natural. )
As you know, the light has no mass, so the gravity (= m × g ) should be zero. But the general relativity changes the subjects about the object with mass into that of no mass light, as shown in Fig.10.
So in the general relativity, the observer has the power of erasing gravity of the object !
But if we can NOT use the usual special relativity moving into the Minkowski spacetime, the general relativity is meaningless.
So even in the general relativity, the special relativity is indispensable.
This means if the special relativity is wrong, the general relativity is wrong, too.
( Of course, as the special relativity can not describe the gravity, the general relativity is also indispensable in the relativistic theory. )
First we explain the basic rules in the Lorentz transformation.
If you have not read about the special relativity, see this page first.
(Fig.5) Two inertial reference frames ( K and K').
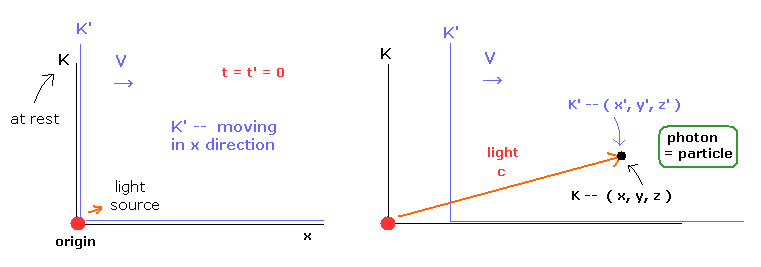
We suppose two inertial reference frames K and K' as shown in Fig.5.
The reference frame K' is moving in the x-direction at the velocity v with respect to K.
Each space time coordinate is ( t, x, y, z ) in K, and ( t', x', y', z' ) in K'.
At the time of t = t'= 0, the origins of these two inertial coordinate systems are located at the same point in space.
And at t= t' = 0, the light is emitted from the source of the origin.
If the light speed is " c " in any reference frames, the following equations are satisfied.
(Eq.1)
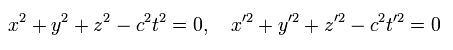
where t and t' are the time in K and K' reference frames, respectively.
When (x', y', z', t' ) of K' satisfy the relations of
(Eq.2)
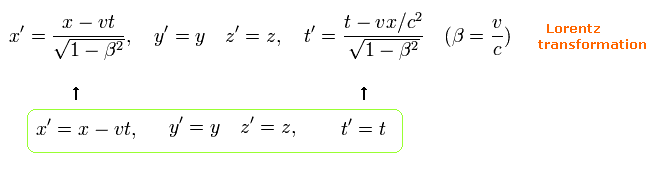
Substituting Eq.2 into Eq.1, we can confirm that Eq.1 is satisfied.
(Eq.2')
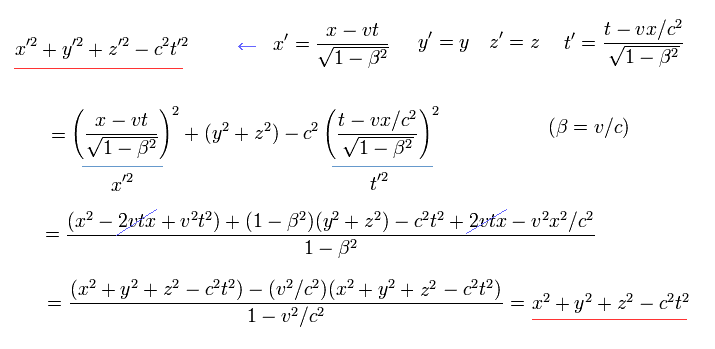
Eq.2 is called "Lorentz transformation" of boost in the x direction.
Generally, the scalar length (= s2 or ds2 ) is expressed as a square of four-vector interval of
(Eq.3)
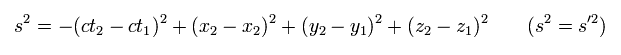
Lorentz transformation of Eq.2 can be expressed using the matrix, as follows,
(Eq.4)
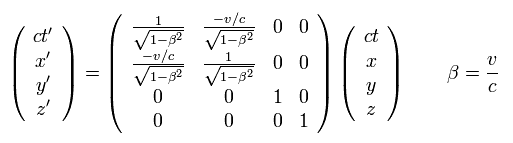
So it is convenient to use x0 = ct instead of t, as a time variable.
(Eq.5)
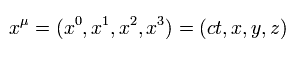
When the index (= 0, 1, 2, 3 ) is at the upper position like Eq.5, this is called a contravariant vector.
Using Eq.5, the Lorentz transformation of Eq.4 can be expressed as
(Eq.6)
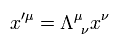
where the Lorentz matrix is
(Eq.7)
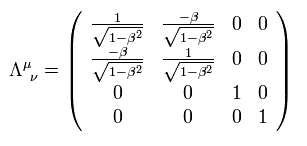
If we use the same variable twice in one term (like ν of Eq.6 ), this means the sum of ν = 0 + 1 + 2 + 3.
For example, using Eq.7, ct' is
(Eq.7')
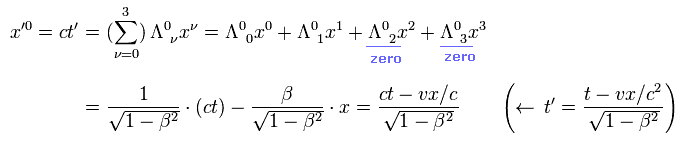
this is equal to Eq.2.
And we define the Minkowski metric tensor, as follows,
(Eq.8)
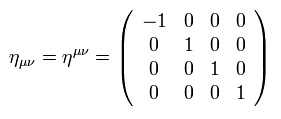
Caution: in this page, η means the Minkowski metric tensor, so "g" means the general metric tensor, which is a function of four-vector xμ.
Using this Minkowski metric tensor, a covariant vector is
(Eq.9)
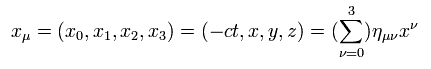
So when the index is at the lower position, only x0 = - ct is minus.
Eq.8 and Eq.9 mean
(Eq.9')
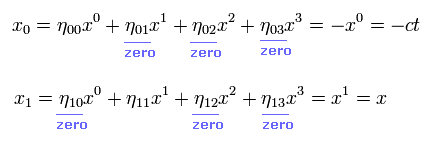
Using these contravariant and covariant vectors, the scalar length of Eq.3 is
(Eq.10)
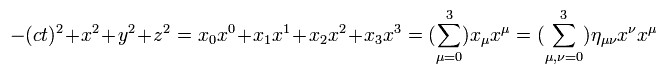
From Eq.8
(Eq.11)
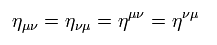
and
(Eq.12)
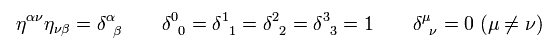
where δ means "Kronecker delta". Eq.12 means η η = identity matrix.
Eq.6 can be expressed as
(Eq.13)
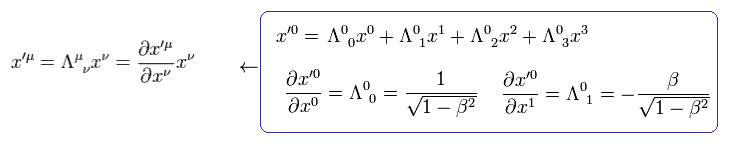
Eq.13 is transformation of contravariant vector.
From Eq.10 and Eq.13, and the fact that the scalar length doesn't change under Lorentz fransformation,
(Eq.14)
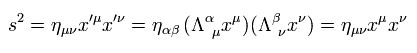
So
(Eq.15)
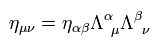
From Eq.8
(Eq.16)
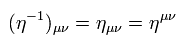
A inverse matrix × matrix is an identity martix in both metric tensor and Lorentz matrix, as follows,
(Eq.17)
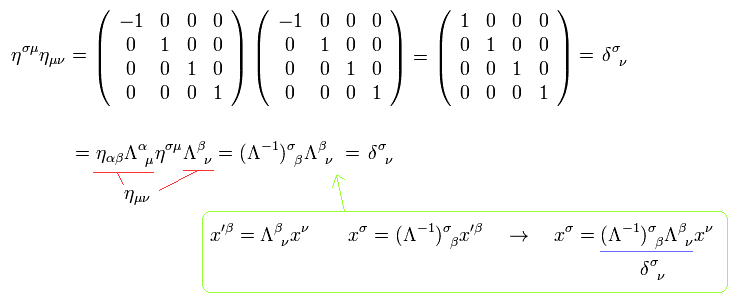
here we use Eq.15.
From Eq.17, the inverse matrix of Lorentz transformation is
(Eq.18)
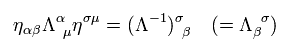
Using Eq.18, the covariant vector of Eq.9 changes under Lorentz transformation, as follows,
(Eq.19)
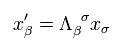
Here we prove Eq.19. Using Eq.18, Eq.19 is
(Eq.20)

From Eq.9 and Eq.12, η × covariant vector = contravariant vector.
Multiplying both sides of Eq.20 by ησ β,
(Eq.21)
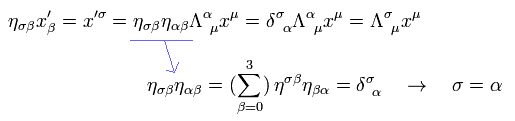
This is the same as Eq.13. As a result, Eq.19 is true.
From Eq.18, the transformation of covariant vector (= Eq.19 ) can be expressed as
(Eq.21')
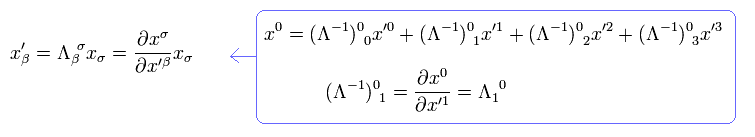
Next we prove that the partial differential operator changes as covariant vector under Lorentz transformation.
(Eq.22)
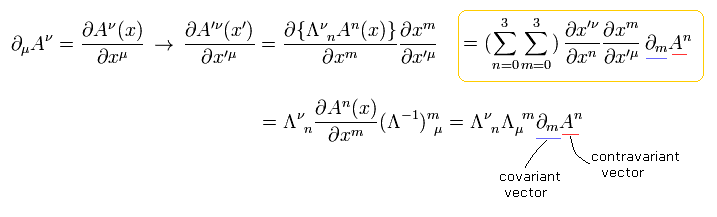
where we use Eq.18 and the inverse relation of Eq.13.
Eq.22 means partial differentiation of vector Aν is what we call "tensor".
In Eq.22 case, Aν changes as a contravariant vector, and partial differential operater changes as a covariant vector under Lorentz transformation.
So the index (= μ) of partial differential operater is at the lower position in Eq.22.
Basically, mixed tensor changes under Lorentz transdormation, as follows,
(Eq.23)
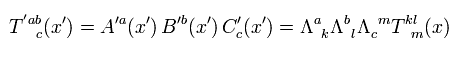
As I said above, according to the relativity, the electromagnetism was said to be incorporated into the relativistic theory correctly.
But is it really so ??
General relativity is dependent on local Lorentz symmetry. So if the special relativity in the electromagnetic fields is wrong, the general relativity is wrong, too.
Maxwell's equations are
(Eq.24)
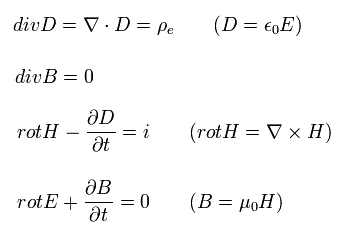
where E and H mean the electric field and magnetic field, respectively.
And D and B means the electric flux density and magnetic flux density.
In this page, the current i is expressed as Jμ, too ( μ = 1, 2, 3 ).
In the relativistic theory, the electric and magnetic field are expressed using vector (= A ) and scalar (= φ) potential of
(Eq.25)
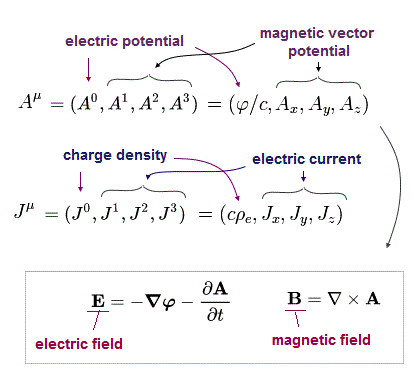
where ρe and J mean charge density and current density, respectively.
If we don't define these vector and scalar potentials, charge and current density as relativistic four-vectors, the electromagnetism does NOT satisfy the relativistic theory.
But these definitions of Eq.25 cause very mysterious and strange phenomena by observer's simple movement, as is explained later !
( See also Special relativity breaks down in electromagnetism ! )

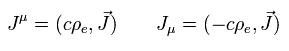
Using these vector and scalar potential, electric (E) and magnetic (B) fields can be expressed as
(Eq.26)
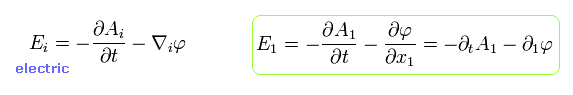
(Eq.27)
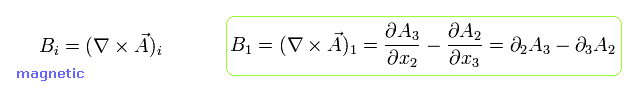
We define the antisymmetric tensor ( Fμ ν ), as follows,
(Eq.28)
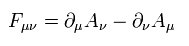
where A means the vector or scalar potentials.
The partial derivative symbols of space coordinates (i = 1, 2, 3) are expressed as,
(Eq.29)
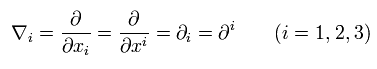
So, as I said, Eq.29 doesn't change depending on the index position.
The partial derivative of the zero component (= time ) is
(Eq.30)
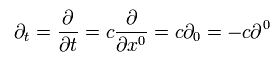
When the index " 0 " is at the upper position, the time derivative becomes minus.
Because as I said in Eq.22, ordinary derivative is a covariant vector.
From Eq.26, Eq.27 and Eq.28, the electric (= E) and magnetic (= B) fields are expressed as
(Eq.31)
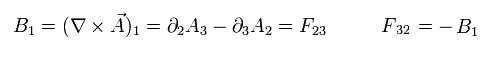
(Eq.32)
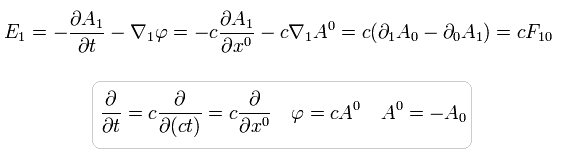
where A0 = - A0 = φ/c.
From these manipulations and definitions, we can imagine that they tried to combine relativity with electromagnetic fields somehow.
Basically, the charge density and current density (= charge flow ) need to satisfy
(Eq.33)
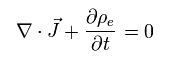
According to the relativity, the total charge is conserved irrespective of the observer's movement.
So the equations of Eq.33 must be Lorentz-invariant.
( Of course, if we admit "earth ether", Lorentz transformation and four-vectors do NOT need to be used. )
Eq.33 can be expressed using four vector ( xμ ), as follows,
(Eq.34)
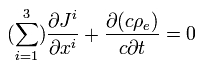
ct can be replaced by x0
where the four vector (= four current density ) is
(Eq.35)
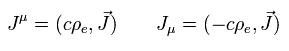
Eq.34 can be expressed as
(Eq.36)
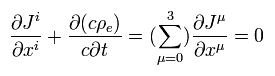
So Eq,36 is a pair of contravariant (= Jμ ) and covariant (= derivative ) vectors, which form Lorentz invariant scalar.
Here we prove Eq.36 is scalar.
Under Lorentz transfomation, the differentiation by xμ is
(Eq.37)
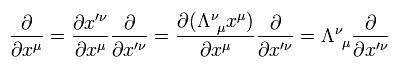
Substituting Eq.37 into Eq.36, we can get
(Eq.38)
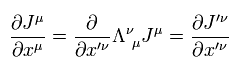
As a retult, Eq.36 (= Eq.33 ) proves to be Lorentz invariant.
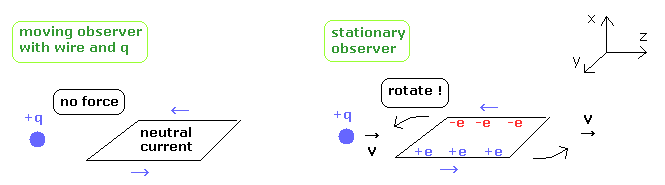
(Fig.6) Observer's "supernatural" power !
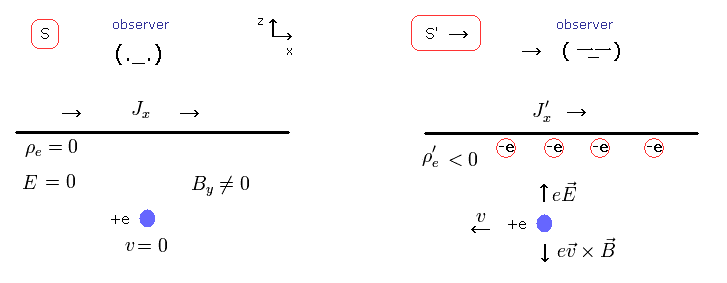
In Fig.6, the electric current Jx contains the plus protons and minus electrons of the same number.
So this current J is constant and neutral. ( So the charge density ρ is zero.)
In S frame of Fig.6, the oberver and charge +e are at rest. So this charge does NOT receive any external force. ( eE = evB=0 )
But in S' frame of Fig.6 in which the observer starts to move to the right at the constant velocity v, the charge +e is moving in the opposite (= left) direction at v from the observer's viewpoint.
So this charge +e receives Lorentz magnetic force (= evB ) from the current J.
But in this case, the charge +e is moving downward depending on the observer's movement.
To avoid this contradiction, the relativity defines the relativistic four-vector relation of Eq.25.
Strange to say, in this theory, the minus charge is generated spontaneously in the neutral place depending on the observer's movement !
( Of course, as I said, the plus and minus charges existing here are equal to each other in number ! )
The vector potential, scalar potential, charge density, and currenrt density of Eq.25 change like Eq.6 and Eq.7 (Eq.25-2) under Lorentz transformation, because they are four-vectors.
(Eq.39)
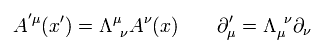
The constant current J is neutral and in the x direction in the left of Fig.6. So the charge and current densities are
(Eq.40)
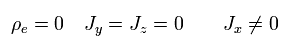
As a result, the magnetic field in the y direction ( By > 0 ) is generated ( the electric field E is zero ).
(Eq.41)
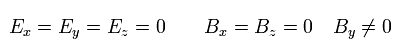
Using Eq.26, Eq.27, and Eq.39, the electromagnetic fields from the observer moving to the right ( S', right figure of Fig.6 ) is
(Eq.42)
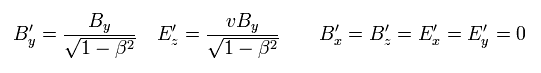
Here we prove Eq.42.
From Eq.40, constant and uniform electric current J is in the x direction, so the vector potential A is
(Eq.42-2)
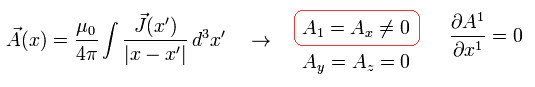
Considering A0= ( φ/c ) = A2 = A3 = 0, Eq.25-2, Eq.42-2, and inverse Lorentz transfromation ( change -v to +v in Eq.4 ),
the electric field in the x direction transforms under Lorentz transformation as
(Eq.42-3)
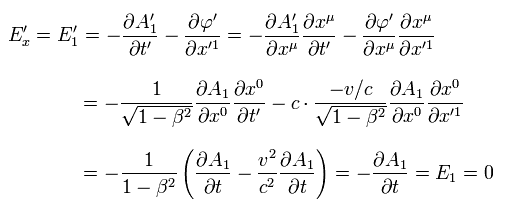
where we use x0 = ct, and β = v/c.
Eq.42-3 means the electric field Ex doesn't change under Lorentz transformation (= 0).
In the case of magnetic field,
(Eq.42-4)
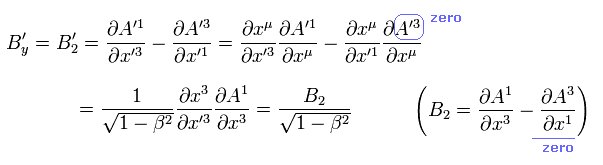
In the same way, we can prove Eq.42.
As a result, also when the observer is moving, the charge +e doesn't move in the z (or y ) direction, because Lorentz force (= evB ) is equal to the electric force (= eE ), as follows,
(Eq.43)
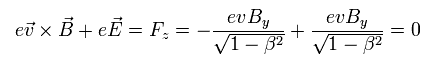
But why the neutral place can generate the electric field (= E ), though the minus and plus charges of the equal number exist there ??
The trick exists in the four-vector relation of charge and current densities of Eq.25.
From the viewpoint of the moving observer, these things look , as follows,
(Eq.44)
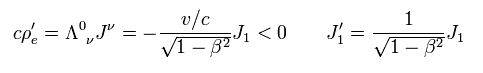
Surprizingly, Eq.44 means the minus charge is generated, though the observer does NOT do anything to the current !
(Fig.7) Observer's "power of looking" causes the electric charge ??
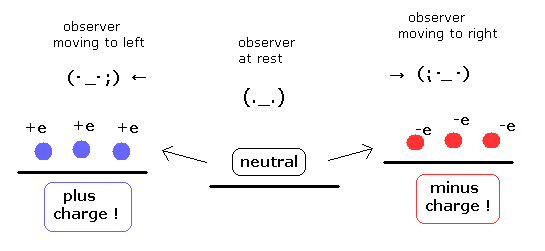
As shown in Fig.7, the neutral current can generate minus or plus charges depending on the observer's moving direction !
This is very strange.
(As I said, this strange phenomenon originates in Lorentz transformation itself. )
Basically, the neutral current i is the relative motion between plus and minus charge, as follows,
(Fig.8) Neutral charge remains neutral !
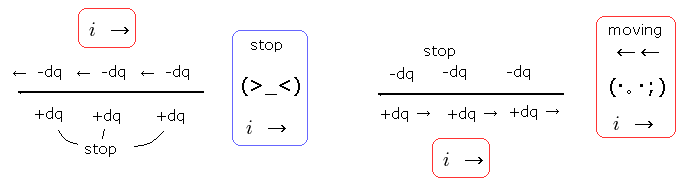
It is quite natural that neutral things remain neutral if we don't give anything to it.
This is the most important trick in the relativistic electromagnetic theory.
If we deny these strange phenomena, it means special (general) relativity and QED are wrong.
According to ordinary textbooks, from the viewpoint of the moving observer, the electric wire is contracted (= Lorentz contraction ).
And the charge density ρ becomes bigger under Lorentz transformation of Eq.7. ( charge density is one of the four-vectors. )
As a result, the total charge = charge density × electric wire length is NOT changed under Lorentz transformation.
But this explanation is inconsistent with the above definition of Eq.44.
The ordinary textbooks say only about one charge's viewpoint ( plus or minus ).
If this comment is true, both plus and minus charge densities become bigger under Lorentz transformation, because both charges are in the same Lorentz-contracted electric wire.
In Eq.44, Only minus charge density is increased, though both charges are in the same one electric wire.
So the relativistic electromagnetism completely violates the total charge conservation.
See also Special relativity breaks down in electromagnetism !
-----------------------------------------------------------------------------------------
(Fig.W-1) Electric wire loop rotates or not ??
A recent interesting report showed that Lorentz force is inconsistent with special relativity.
( Masud Mansuripur, Trouble with the Lorentz law of Force: Incompatibility with Special Relativity and Momentum Conservation. Phys.Rev.Lett 108, 193901, 2012.)
This paper seems to use the violation of the above total charge conservation at the two lines (= z direction ) of the electric current loop (=in the z-y plane).
As shown in Eq.44, the plus or minus charge densities suddenly appear in the neutral electric current wire from the viewpoint of stationary observer.
In this case, the wire and charge q are moving at the velocity v in the z direction. So from the stationary observer, these wire is moving in the z direction.
As the two z-direction electric flows in one wire are opposite to each other, which causes the opposite charge densities ( + or - ).
So another charge q rotates this electric dipole from the viewpoint of the stationary observer.
Though from the moving observer with the wire and the charge q, it is NOT rotated.
This is clearly paradox, and it means special relativity can NOT deal with the directions other than Lorentz force law of Eq.43.
To solve this paradox, we have to define "virtual" center of rotation.
So basically, this paradox has NOT been solved yet.
( See also " hidden momentum" method can really solve this paradox ?? )
From Eq.24, we can derive the vacuum electric and magnetic energy.
( See also this page. )
The inner product of E and the third equation of Eq.24 and the inner product of H and the fourth equation of Eq.24 are
(Eq.45)
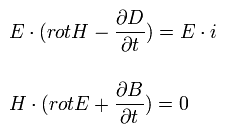
The upper equation minus the lower equation of Eq.45 is
(Eq.46)
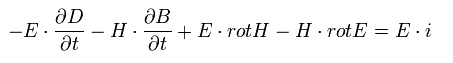
Using the formula of
(Eq.47)
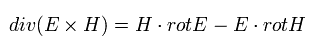
and the relation of
(Eq.48)
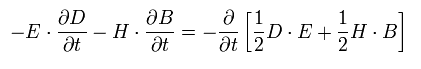
and the definition of
(Eq.49)
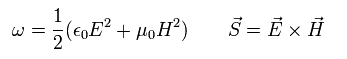
we obtain ( current density i = 0 in the vacuum )
(Eq.50)
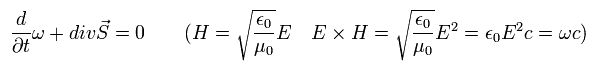
So they insist that Eq.50 means the relation between the electromagnetic field energy (= ω ) and its current ( S = Poynting vector ).
But as shown on this page, the electromagnetic field energy around a single electron (or proton) does NOT represent ω of Eq.49.
Because the electric energy of Eq.49 means the potential energy among infinitesimal charges (= dq ) included in a single electron.
But a single electron can NOT be broken into pieces, and the charge e is NOT made from smaller infinitesimal charges !
(Fig.9) A single electron -e = -dq -dq -dq -dq ...?
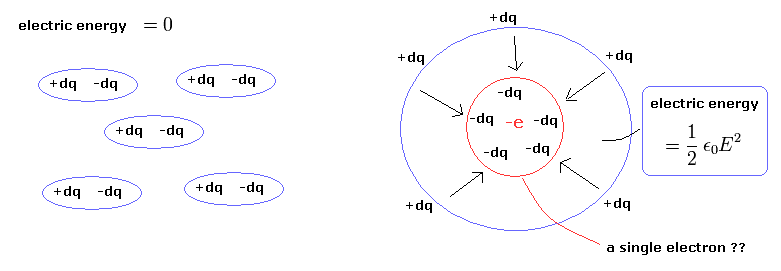
This is one of misunderstandings about Bohr's electron radiating energy.
In fact, the special (and general) relativity is completely dependent on the vacuum electric and magnetic energy of Eq.49.
( If ω of Eq.49 does not mean energy, the relativistic theory ( and QED) doesn't satisfy relativistic energy-momentum tensor ! )
The concept of the energy-momentum tensor is very important also in the gravity of the general relativity.
Eq.51 - Eq.70 are moved into this page (last section).
As I said above, special relativity can not explain gravity like electromagnetic field.
(But the relativistic enectromagnetism depends upon very strange four vectors, as I explained above. )
So we have to think about the spacetime influenced only by the gravity.
( This means if we can erase gravity, this specetime is equal to Minkowski Lorentz invariant frame. )
To erase the gravity, our observer have to fall following the gravity, as I said in Fig.4 right (= free fall ).
( This is called local inertial reference frame, in which the special relativity is valid. )
From the viewpoint of the observer at rest (= not falling ) in the gravitational world, the scalar length is
(Eq.71)
where the definition of Eq.79 is used.
This scalar length value needs to be the same as Eq.3 of Minkowski spacetime.
This means gμν(x) (= "generalized" metric tensor ) is related to the "connection" between Riemann and Minkowski spaces.
Of course, this connection is related to gravity.
If we fall following the gravity as shown in the right figure of Fig.4, this gμν is equal to Minkowski metric tensor of Eq.8.
( You should keep in mind that this generalized scalar and gravity cancellation are ONLY artificial definitions. )
And very strong restrictions based on this definition make the present quantum field theories such as string theory only mathematical (NOT physical) languages. ( See also this page. )
And the general coordinate transformation including acceleration is
(Eq.72)
Eq.72 is generalized version of transformation of contravariant vector (see Eq.13).
As you know, in the special relativity, this transformation must be like Eq.4, which does not include acceleration.
When this transformation is acceleration, f(x) is two times differentiable.
( Lorentz transformation of Eq.6 is only one time differentiable. In this case, partial derivative is Λ of Eq.7. )
Our goal is to move into Minkowski reference frame by accelerating in the direction of gravity like right of Fig.4.
If we don't transfer to Minkowski spacetime, the general relativity is meaningless.
Partial derivative in Riemann space (in the same way as Minkowski space ) is
(Eq.73)
Eq.73 is generalized covariant vector.
See also Eq.21'.
Like Eq.14, substituting Eq.72 into Eq.71, we obtain
(Eq.74)
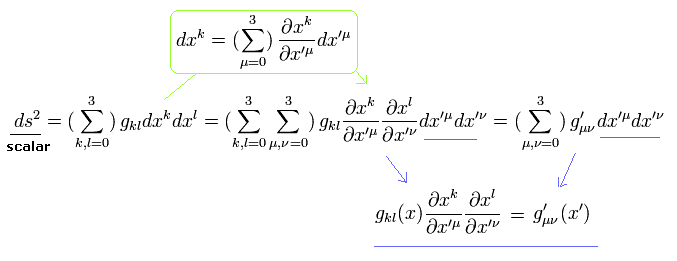
So metric tensor g changes as the second-rank tensor.
( This is the reason why it is called "tensor". )
If we move into Minkowski spacetime by the general coodinate transformation of Eq.72 and Eq.73, this metric tensor becomes Minkowski metric tensor ( locally ), as follows,
(Eq.75)
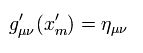
This definition is based on the artificial assumption that gravity is cancelled by observer's acceleration.
From Eq.74 and Eq.75, considering each determinant (= determinant × determinant × ... ),
(Eq.76)
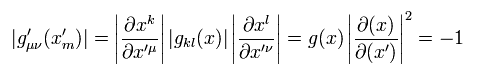
where we use the Minkowski metric tensor determinant = -1, as shown in Eq.8.
So the determinant g(x) of the generalized metric tensor is minus, as follows,
(Eq.77)
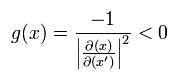
And we define gμν, as follows,
(Eq.78)
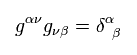
Generally, unlike Minkowski metric tensor of Eq.8, gμν is not equal to gμν
And Eq.78 satisfies
(Eq.79)
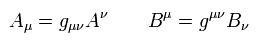
where Aν and Bμ are contravariant vector, and Aμ and Bν are covariant vector.
Eq.79 can be confirmed by
(Eq.80)
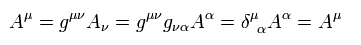
On the page of Derivation of Riemann, Ricci, Einstein tensors , we get the important relations of
(R-1) Parallel transport of covariant vector.
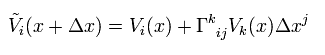
(R-2) Parallel transport of contravariant vector.
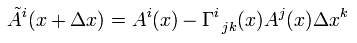
(R-3) Christoffel symbol by the metric tensor -1.
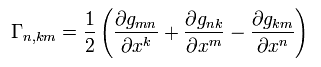
(R-4) Christoffel symbol by the metric tensor -2.
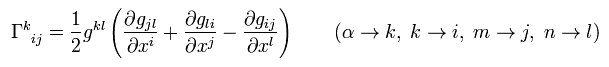
(R-5) Christoffel symbol coordinate transformation..
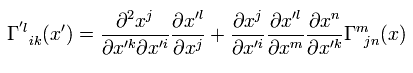
(R-6) Covariant derivative of the covariant vector..
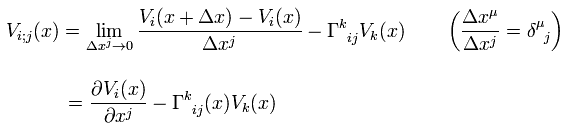
(R-7) Covariant derivative of the contravariant vector..
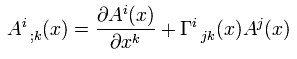
(R-8) Riemann's curvature tensor.
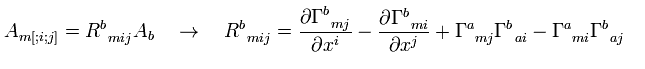
(R-9) Riemann's curvature tensor's symmetry.
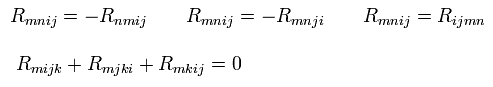
(R-10) Ricci tensor.
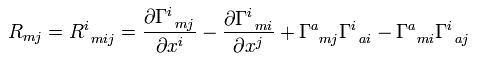
(R-11) scalar curvature.
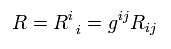
(R-12) Bianchi identiry.
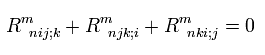
(R-13) Einstein tensor..

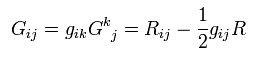
(R-14) Ricci tensor by Einstein tensor..
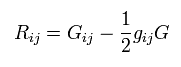
If you have not read Riemannian geometry, read this page first.
In the relativity, the velocities (= u(t) ) in differernt inertial frames are different.
(Eq.81)
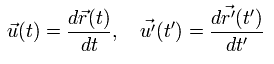
So, instead of dt if we use the proper time (= τ ) of
(Eq.82)
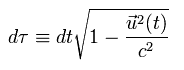
It is very convenient. ( See this page. )
Because this proper time is the time with the moving object itself, which is Lorentz invariant scalar, as follows,
(Eq.83)
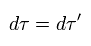
Instead of Eq.81, we use the next four vector velocity (= ω ), which changes as four vector under Lorentz transformation,
(Eq.84)
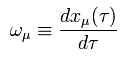
Lagrangian of the free particle in inertial frames can be expressed as ( using Eq.82 )
(Eq.85)
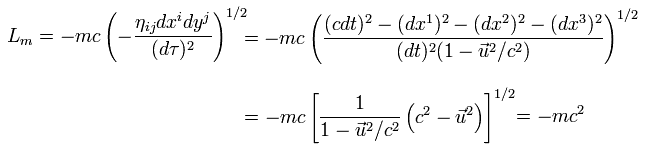
Lagrangian of Eq.85 is Lorentz invariant scalar, which means the equation of motion is valid in all reference frames.
Minimizing the action S, we get Euler-Lagrange equaion, which means the equation of motion.
(Eq.86)
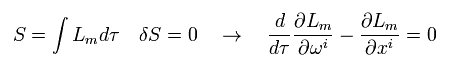
From Eq.84, Eq.85 and Eq.86, we obtain the free particle equation of motion,
(Eq.87)

For example, 1 component is
(Eq.87-2)
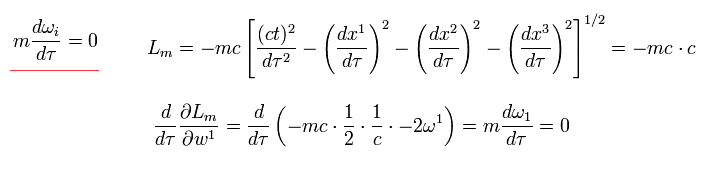
Like Eq.85, we can define the (free) particle only under gravity using the metric tensor g of Eq.71
(Eq.88)
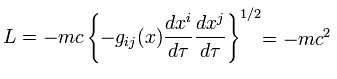
of course, Eq.88 is scalar.
here,
(Eq.89)
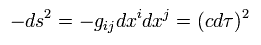
So Lagrangian (= -mc2 ) of Eq.88 under gravity is equal to Eq.85.
The variation of the action in Eq.88 is
(Eq.90)
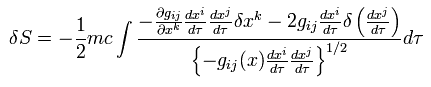
where the second term of the numerator is
(Eq.91)
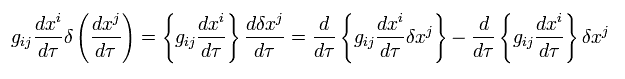
From Eq.88, the denominator of Eq.90 is c, so Eq.90 becomes
(Eq.92)
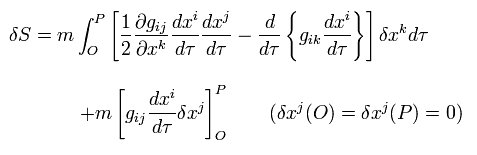
where the second line is zero.
And the second term of Eq.92 is
(Eq.93)
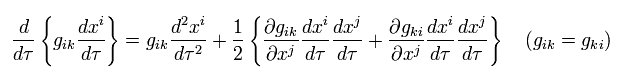
where we divide the second term into 2 terms.
Inserting Eq.93 into Eq.92, and when its variation is zero,
(Eq.94)
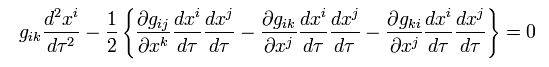
Multiplying Eq.94 by gmk, the first term becomes
(Eq.95)
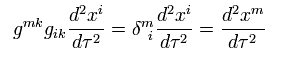
And using R-4 (= Christoffel symbol ), the other terms of Eq.94 become
(Eq.96)
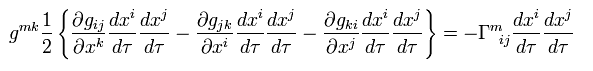
From Eq.94, Eq.95 and Eq.96, we get the equation of motion only under gravity,
(Eq.97)
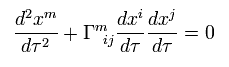
where the second term means gravitational acceleration (= g).
So as I said, Christoffel symbol ( which consists of the generalized metric tensor gμν ) is related to the gravity.
Using the four velocity ω of Eq.84, Eq.97 becomes
(Eq.98)
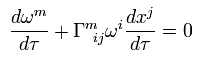
So
(Eq.99)
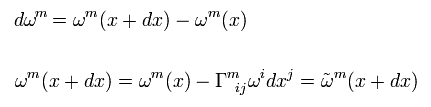
Using R-2, the four velocity ω only under gravity do parallel transport.
So as I said, the parallel transport means the moving particle receiving only gravity.
In fact, when the gravitational field is complicated, it is unrealistically difficult to get the equation of motion under gravity.
So we have to use a kind of approximation (= under very weak static gravity ).
(But I think this approximation omits too much. )
So in this very weak gravity, the metric tensor is almost same as Minkowski η, as follows,
(Eq.100)

And we suppose this metric tensor doesn't depent on the time variable (= static ), as follows,
(Eq.101)
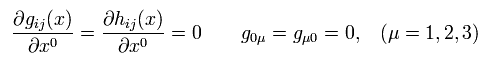
And we suppose gμ 0 are all zero ( μ = 1, 2, 3 ).
Furthermore, we suppose the particle's velocity (= ωμ, μ = 1, 2, 3 ) is very slow,
(Eq.102)
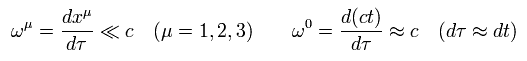
Neglecting the second order of the infinitesimal value (such as h(x) × h(x) ), using Eq.100, Christoffel symbol of R-4 becomes
(Eq.103)
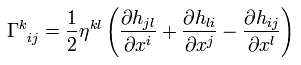
Inserting Eq.103 into the equation of motion (= Eq.97 ) under gravity, and considering the velocity is infinitesimal,
(Eq.104)
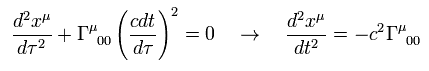
As shown in Eq.102, ωμ × ωμ (μ = 1, 2, 3) is approximately zero.
Considering Eq.101 and Eq.103,
(Eq.105)
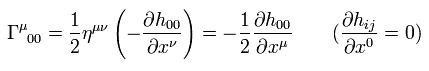
where μ should not be zero.
From Eq.104 and Eq.105, we get
(Eq.106)
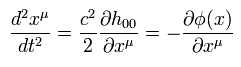
where φ(x) means the gravitational potential.
From Eq.106, h00 and g00 can be expressed by the gravitational potential, as follows,
(Eq.107)
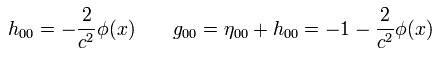
Like the electromagnetic field, we introduce the energy momentum tensor also in the gravity case.
( So if the energy-momentum tensor of the electromagnetic field is meaningless, the gravity case is meaningless, too. )
When we use Einstein tensor of R-13 as energy-momentum tensor, this equation is called Einstein's gravitational field equation.
(Eq.108)
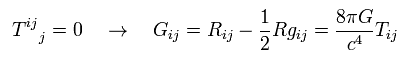
The energy density T00 means the mass energy density, so
(Eq.109)
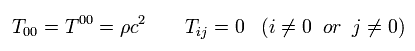
where ρ is mass density.
Here we confirm whether Eq.106 is satisfied or not also in Eq.108 in the very weak static gravitational condition.
Multiplying Eq.108 by gij,
(Eq.110)
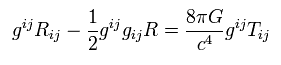
And using the definitions of
(Eq.111)
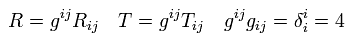
(where we use Eq.78)
Inserting Eq.111 into Eq.110, and using 108,
(Eq.112)
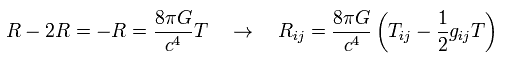
From Eq.78, infinitesimal metiric tensor can be expressed as
(Eq.113)
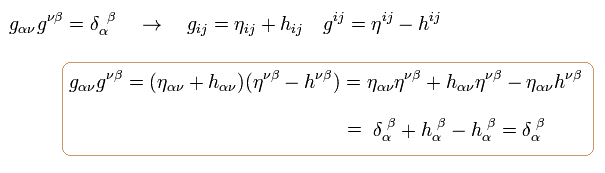
In the static vacuum, all Tμν except for T00 are zero, so,
(Eq.114)
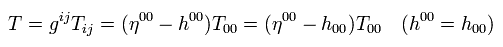
Inserting Eq.114 into R00 of Eq.112,
(Eq.115)
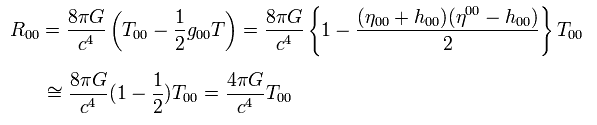
where we use η00 × η00= 1, and neglect the second order infinitesimal values.
Using Ricci tensor of R-10,
(Eq.116)
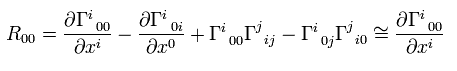
where we use the conditions of Eq.101 and Eq.103, neglect the second-order infinitesimal values.
From Eq.103 and Eq.116,
(Eq.117)
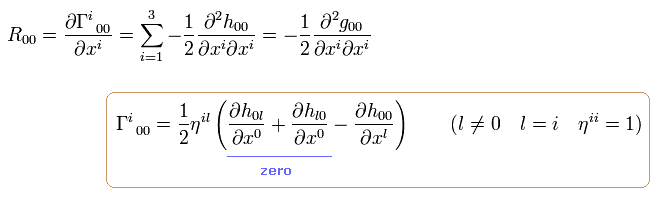
From Eq.107, Eq.109, Eq.115 and Eq.117, we get
(Eq.118)
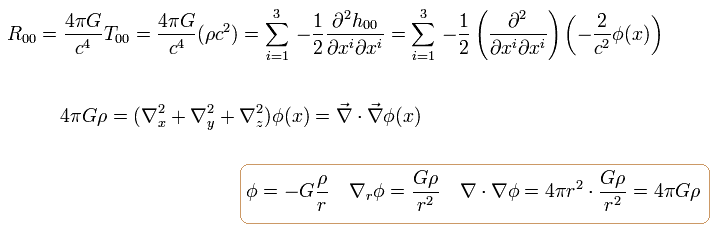
Eq.118 is equal to the gravity of Newtonian mechanics.
To match Newtonian mechanical gravity, we choose Einstein gravitational field equation of Eq.108.
So it is quite natural that Einstein's gravity is equal to Newtonian mechanics.
And as shown in this section, general relativity omits too much in the approximation.
( Can we insist general relativity is really correct in this very abstract approximation ? )
Considering the covariant derivative of the metric tensor g is zero ( see Eq.51 of this page ), we can add other terms to Eq.108 like
(Eq.119)
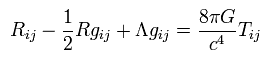
This Λ is called "cosmological term" or "consmological constant".
But Eq.119 is not consistent with Eq.118 of Newtonian mechanics.
So when this consmological constant is very small, we can use Eq.119.
Schwarzschild solution (metric) was the first solution of Einstein equation in 1915 and predicts the existence of black hole.
( But unfortunately, the black hole has not been found yet directly. )
In this case, point particle of mass M is at the origin, and the gravitational field is spherically symmetric and static.
( So, Schwarzschild metric thought about the things like the earth from the beginning. )
Using the polar coordinate of
(Eq.120)
See the detailed calculation method in Schwarzschild solution and GPS paradox.
The important point is the time component.
(Eq.124)
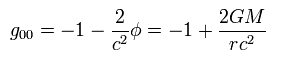
So
(Eq.125)
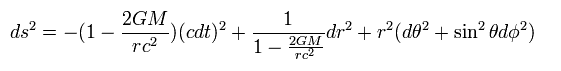
From Eq.125, when the radius r is less than
(Eq.126)
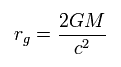
g00 becomes plus, which measn space-like.
This radius of Eq.126 is called Schwarzschild radius, which is related to "black hole".
So black hole is inconsistent with the relativistic causality.
( But they do not give up general relativity. Why? )
Of course, Einstein himself did NOT believe black hole.
If we give up relativity, it means relativistic Dirac equation needs to be replaced by other things.
So they could not abandon the general (and special) relativity.
This is a main reason why the strange black hole, which contradics relativity, has survived.
From Eq.89, the proper time is
(Eq.127)
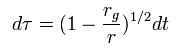
where dt is the time at infinity (= gravity is zero ).
Eq.127 means as gravity is stronger, the time is delayed. But in this real world, is it really possible ??
Fig.10 is easy to imagine.
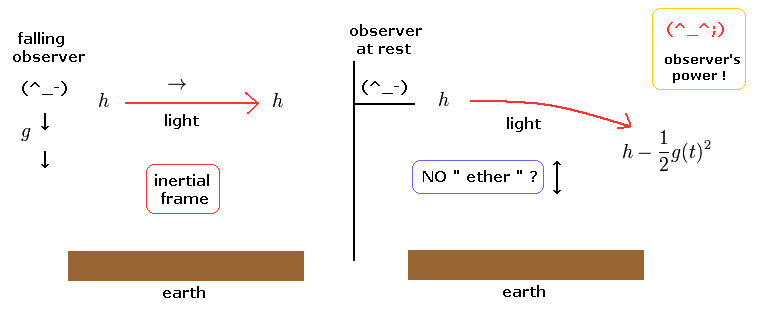
When the observer is falling to the earth obeying the gravity, the light acts as that of Minkowski inertial frame (left of Fig.10).
This means when the observer is at rest with respect to the earth, the light is bent by 1/2 gt2 to the earth, though the light has no mass.
So as we get closer to the earth (= gravity is stronger ), the time is delayed and the light moves slower, which bends the light toward the earth.
But there are some strange points in this explanation.
First, As I said in Fig.4, even if the observer is falling to the earth, the gravity acting on the object is NOT erased.
So the observer's "looking power" is "supernatural", like the case in which the observer can generate the electric charge only by looking ( see Fig.7 ).
In conclution, the observer's existence is too special for the theory of relativity, which is similar to the quantum mechanics.
And at first, the local inertial frame was defined with respect to the objects with mass, as shown in Fig.4. But without knowing it, the subjects are changed into no mass light. This is strange.
And according to the relativity, the ether is prohibited. Then why the light with no mass is bent by gravity, though the vacuum contains Nothing.
This is strange.
(Fig.11) General relativity by the "earth ether".
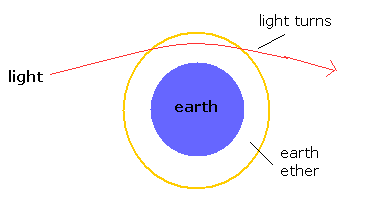
As I said on this page, if we admit the earth ether which is attracted to the earth, we can explain Michelson-Morley experiment.
In the same way, it is quite natural the light turns to the gravity when the ether (= light medium ) is attracted to the gravity.
Or if we consider the dielectric substance around the earth, the light speed is slower, as the light is closer to the earth.
If the time is delayed, the time period of the electromagnetic wave is said to be longer (= light frequency is smaller ).
So they say when the light is emitted from the gravitaional field of the star, its wavelength is longer (= red shift ) at the point far away from the star.
But is the time (clock) delay really occurring ??
As I said, if the light medium (= ether ) is attracted to the gravity, as the light is closer to the star, it tends to stay there.
( As a result, the wavelength of the light emitted from the star is elongated. )
So the ether attracted to the star can explain the gravitational red shift.
( Of course, if we consider the dielectric substance close to the star, the wavelength of the light which goes away from the star becomes longer )
Or we can consider the light energy loss ( or gain ) by the gravity, which influences its frequency.
"Convenient" photon can pass through dark energy, matter, Higgs "uninjured"?
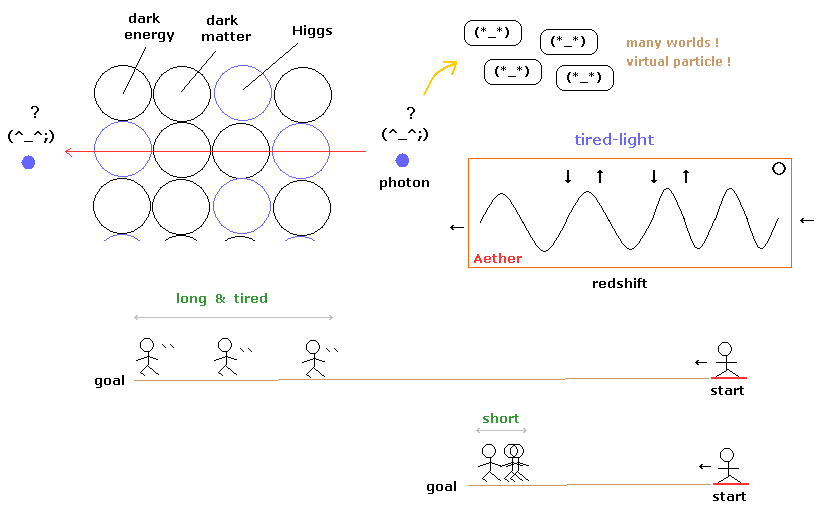
In fact, as you know, the gravity is too weak.
For example, the time difference which is said to be caused by the gravity in satellite is only 38 microsecond per day ( which means the frequency change of light we observe ).
Gravitational experimental results are easily influenced by other factors.
The strange thing such as "time delay" should be the last one we consider to explain the experimental results, I think.
Ordinary textbooks often say that various experiments showed that the general relativity is correct.
But in fact, only a part of the experiments showed this.
For example, the rotation of the galaxy can NOT be explained by the general relativity.
Because even if we consider the overall masses included in the galaxy, it can NOT reach the vast energy needed for rotating the galaxy.
(Fig.12) Dark matter is "rotation of space ether".
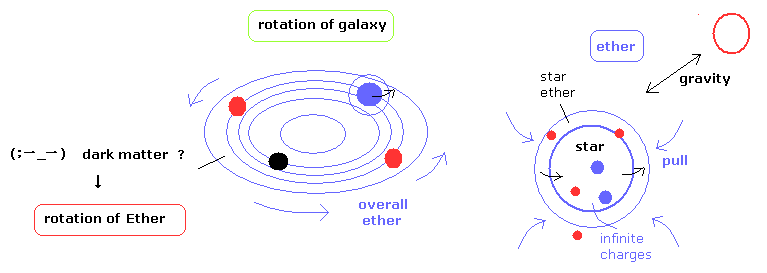
So this means the failure of the general relativity.
To cover this deficit, strange "dark matter" was introduced.
This dark matter (and energy) is said to account for most of the things existing in the universe.
But strange to say, we do NOT know what this dark matter really is, though the space has a large amount of it.
If we admit the ether, we can easily explain these phenomena.
( Of course, to do this, we have to go back to Bohr-Sommerfeld model from Dirac equation, as I said above. )
The rotation of the overall galaxy is caused by the rotation of the space ether. ( Imagine the rotation of the overall water in a cup. )
The star (earth) consists of infinite charges which attract each other by the medium (= ether ), and it is natural that they are moving together.
Generally, things tend to be more stable. In the infinite plus and minus charges, they try to be more stable attracting each other, which drag the ether in (= star ether).
For example, the air inside the plane flying in the air is moving with the plane.
So this can explain the star and space ether's motion.
And the imbalande of a large amount of the charges (= masses) in the universe causes the gravitational force between stars via the space ether.
( And it is natural that we think "neutrino" is a longitudinal de Broglie wave transmitted through the ether. )
---------------------------------------------------------------------
And a recent interesting report insists that the gravity doesn't exist.
( Erik Verlinde, On the origin of gravity and the laws of Newton, Journal of high energy physics, 2011, 4, 29. )
Considering the very weak gravity, it is natural that we think the gravity is "overall" effects including the Coulomb relations and various phenomena, I think.

2012/4/9 updated. Feel free to link to this site.