Home page
Einstein is wrong
electromagnetic paradox (← 5/27/2025 )
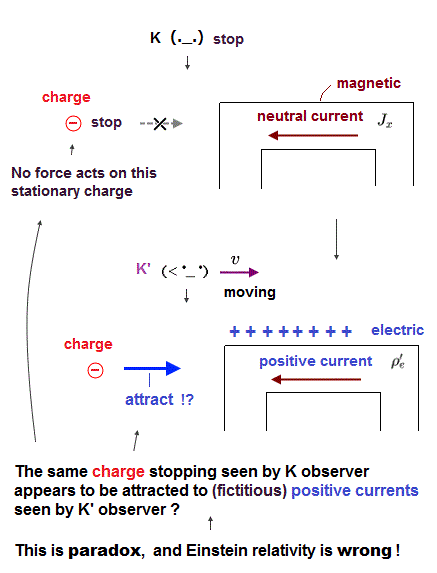
(Fig.1) A stationary observer K sees a neutral electric current in electric wire which appears to be positively-charged and attract and an electron only when seen by a moving observer K'. ← paradox !

Einstein relativity is wrong full of fatal paradoxes such as electromagnetic paradox.
In Fig.1, a stationary observer K sees the neutral electric current flowing in the electric wire which paradoxically appears to be positively charged as seen by an observer K' moving in x direction (= see this page in detail ).
Because according to Lorentz length contraction (= moving objects or intervals become shorter ), the intervals between moving electrons (= - ) seen by K become wider (= lower density of electrons ) seen by the moving K' who sees the electrons at rest ( this case II, III ).
And the intervals between stationary positive nuclei (= + ) seen by K become shorter (= higher density of positive nuclei ) seen by the moving K'.
↑ This is clearly paradox disproving Einstein relativity.
Because as seen by the stationary K observer, the neutral wire cannot attract an external electron, while a moving observer K' sees the same wire positively-charged ( this or this p.2-3 = neutral current J changes into positive charge ρ seen by K' under Lorentz transformation ) and attracting the external electron.
(Fig.2) Lorentz transformation of neutral current (= J ) causes positive charges ρ seen by K', but the electric field E'x around the positive charge remains zero, which is self-contradictory.
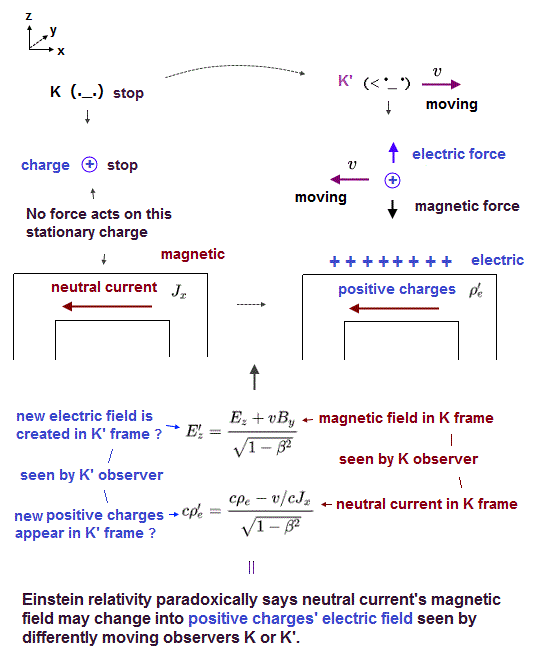
As shown in Fig.1, the relativistic electromagnetism causes fatal paradox where a neutral wire seen by a stationary K appears to be positively-charged seen by a moving K'
In the relativistic Lorentz transformation, the neutral current Jx in K frame unrealistically changes into the electric charge (= ρe', this p.2-3, this-middle-Box 13.6 ) in K' frame, which newly-appearing charges or electric force is needed to cancel the newly-generated Lorentz magnetic force on an external charge (= + ) that is moving (= causing Lorentz magnetic force ) only when seen by K'
But the electric field E'x in K' frame after Lorentz transformation of electric field Ex in K frame remains zero E'x = Ex = 0 or E'|| = E|| = 0 ( this p.14 ) even around the newly-appearing positive charges as seen by K' observer ( see this page in detail ) .
↑ Other E'
↑ This relativistic Lorentz transformation of electric field E is clearly self-contradictory (= inconsistent with Lorentz transformation of other electric field in y,z directions, and charge-current ), disproving Einstein relativity.
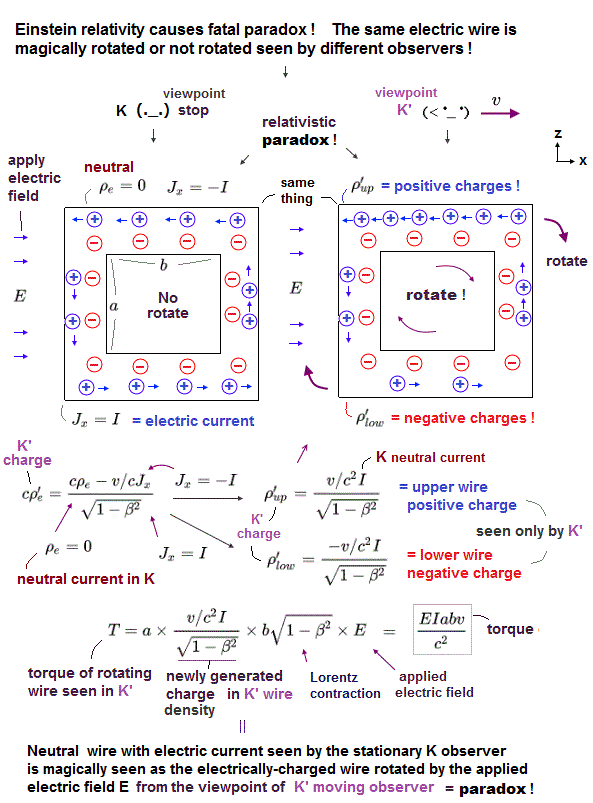
(Fig.3) A neutral wire seen by K appears to be electrically-charged and rotated by electric field E only when seen by a moving K', which fatal paradox has No real solutions.
"Trouble with Lorentz law of force: incompatibility with special relativity and momentum conservation" by Mansuripur is one of relativistic fatal paradoxes in electromagnetic field, which has No solutions.
In Fig.3, a neutral wire (= rectangular circuit ) through which electric current is flowing stops as seen by a stationary observer K under external electric field E (= because the electric field E does not move the neutral wire ).
But according to the paradoxical Einstein relativistic Lorentz transformation, the upper (or lower ) wire of the same neutral circuit appears to be positively (or negatively ) charged only when seen by an observer K' moving in x direction at a velocity v ( this p.5-Figure 2 ).
As a result, only when seen by the moving observer K', the original neutral circuit appears to be electrically-charged and rotated by the external electric field E, which observer-dependent circuit rotation is clearly paradox, disproving Einstein relativity.
↑ First of all, this Einstein relativistic postulate that the neutral wire looks electrically-charged seen by different observers due to Lorentz length contraction is unreal, because the electrically-charged wire should become neutral quickly by the internal electric field inside the circuit (= but if the circuit seen by K' is neutral, the circuit seen by K becomes unrealistically electrically-charged, which relativistic electromagnetism is unreal, wrong from the beginning ).
All the alleged solutions to this obvious relativistic electromagnetic paradox in the rotated electric circuit (= presented by Mansuripur ) are based on unreal assumptions and illusory objects, so No legitimate solutions to this paradox after all.
All these fake solutions are based on the illusory hidden momentum P in z direction allegedly caused by electric charges inside the circuit accelerated by the external electric E in x direction. ← Directions in x (= electric force ) and in z (= resultant momentum ) are contradictory, so this hidden momentum P is unphysical.
↑ And if this (illusory) hidden momentum P in z direction is really generated, the whole circuit would be moved in the z direction (= due to the total momentum P ), which is also paradox, because the neutral circuit is Not moved by electric field E (in x direction ).
Furthermore, these solutions need the unrealistic string connecting the center of the circuit and the moving observer K' to artificially generate hidden angular momentum and (fake) torque canceling the rotation.
As a result, there are No legitimate solutions to this fatal relativistic electromagnetic paradox, so Einstein relativity is proven to be wrong.
(Fig.4) A neutral circuit with electric current I seen by K appears to be electrically-charged (= ρ ) and rotated by (illusory) torque T under electric field E only when seen by the moving K' ? ← This is paradox.
In Fig.4, a neutral circuit through which electric current I is flowing seen by a stationary observer K paradoxically appears to be charged positively (= upper wire ) and negatively (= lower wire ), and rotated by electric field E (= causing torque T ) only when seen by a moving K' observer.
By using the (paradoxical) Lorentz transformation, these new charge densities (= ρ' ) caused from the original neutral current J = ±I in the upper and lower wires can be estimated ( this p.2-3, this p.3-2.2-p.4, this-middle-Box 13.6 ).
From these new (illusory) charge density and the lengths of the circuit (= a × Lorentz-contracted b ), we can estimate the (fake) electric-force torque T rotating the whole circuit by the external electric field E.
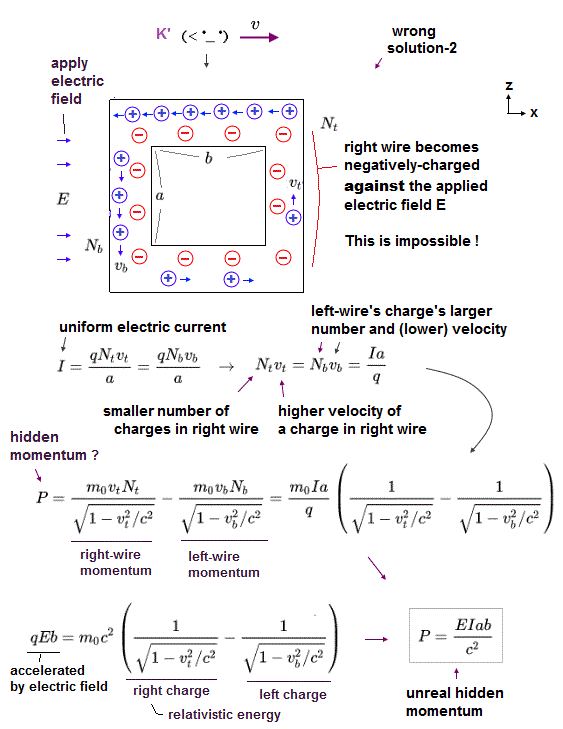
(Fig.5) Charges q in the wire are accelerated in x direction by the electric field E, and increase their (illusory hidden) momentum P in z direction ? ← Directions of force and momentum are inconsistent, so these are wrong solutions.
All alleged solutions to this relativistic electromagnetic paradox are based on the unphysical hidden momentum P ( this p.2-(9) ), so illegitimate.
Here we suppose positive charges q are flowing as electric current I, and negative charges are at rest.
This unphysical momentum P in z direction is said to be caused by electric charges q in wire accelerated in x direction by electric field E. ← Directions of the applied electric force E in x direction and the generated momentum P in z direction are clearly inconsistent, which means this hidden momentum P is unreal ( this p.9-2nd-last-paragraph ).
And if this (illusory) hidden momentum P is really generated, the whole neutral circuit must move in z direction (= because of the momentum P in z direction ) under the electric field E in x direction, which contradicts the real physical principle.
↑ In this solution paper-p.1-right, the electric field force E is in z direction, but the hidden momentum P is in different y direction (= In all these solutions, directions of hidden momentum P and the electric force E must be different, inconsistent and unreal ).
In Fig.5, each electric charge q acquires the energy qEb (= E is electric charge, b is the length of the wire in x direction = these solutions paradoxically did not use Lorentz length contraction of b, so wrong solution ) while moving from left to right wires, which is expressed as relativistic energy (= mc2 ) change.
↑ These charges q accelerated by electric field E in x direction hit the wall of the circuit and push the circuit also in -z direction, canceling the hidden momentum P in z direction (= No hidden momentum P would be generated ).
The electric current in left and right wires must be uniform I = qNtvt/a ( Nt and vt are the number and velocity of charges q in right wire ) = qNbvb/a ( Nb and vb are the number and velocity of charges q in left wire, this p.2-right, this p.2-right ).
(Fig.6) The illusory momentum P × r (= vt = length of an unreal string ) causes the illusory angular momentum and torque canceling the paradox ? ← No !
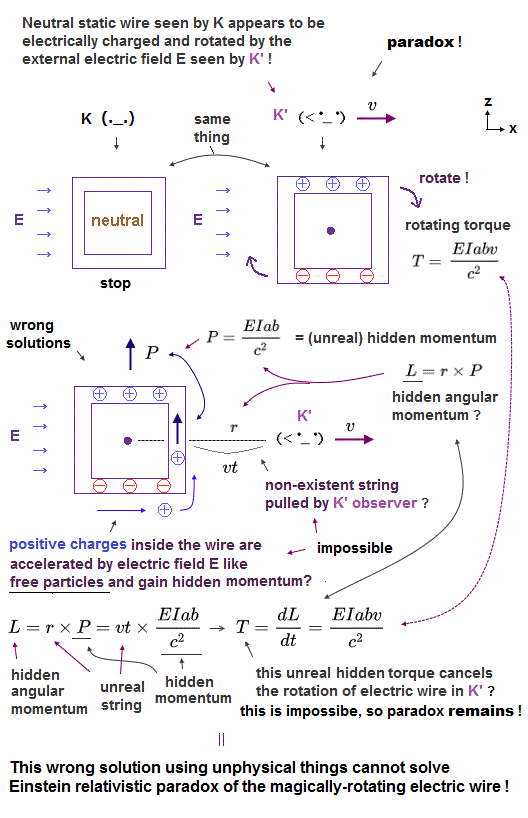
In order to cancel the torque T rotating the whole circuit only when seen by a moving K' observer, all today's (illegitimate) solutions must rely on the unphysical hidden momentum P and an unreal string connecting the circuit and the moving K' causing the hidden angular momentum with K' position being the center of rotation.
↑ The (illusory) hidden angular momentum L is supposed to be equal to the unphysical momentum P × r (= vt = the length of the unreal string changed by the K' observer's motion moving at a velocity v, this p.1-right, this p.3-(15)(16), this p.10-2.5 ).
As a result, this illusory torque T (= time derivative this hidden angular momentum L ) is equal to the torque rotating the whole electrically-charged circuit under electric field E. ← so no paradox in relativistic electromagnetic field ? (= actually still paradox )
↑ First of all, there is No such thing as a string connecting the circuit and the moving K' observer.
And the center of rotations are different between the circuit rotated by electric field E (= circuit's center is the rotation or torque center ) and the circuit pulled by the moving K' (= K' position is the rotation or torque center in the hidden angular momentum P × r = vt ).
As a result, all these solutions based on the illusory string and inconsistent centers of rotations cannot solve the relativistic electromagnetic paradox, and Einstein relativity is false.
electric Lorentz transformation (old)

Feel free to link to this site.