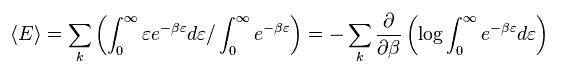
Top page (correct Bohr model including helium )
Strange "spin" is NOT a real thing
Back to Kondo effect page.
(Eq.1)
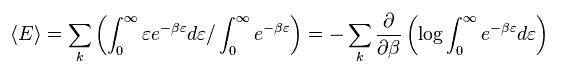
Ther average energy in temperature T can be gotten by multiplying them by Boltzmann factor ( β = 1/kT ).
In Eq.1, the energy (= ε ) is supposed to be a continuous value.
In actual phenomena, the energies are quantized by an integer times de Broglie waves.
Making energy ε discrete,
(Eq.2)
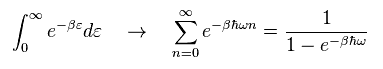
Substituting Eq.2 into Eq.1, we obtain
(Eq.3)
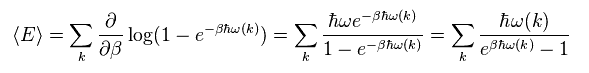
This is called "Bose-Einstein distribution".
(Fig.1) Pauli exclusion principle is a force ? → "Shut up and calculate !"
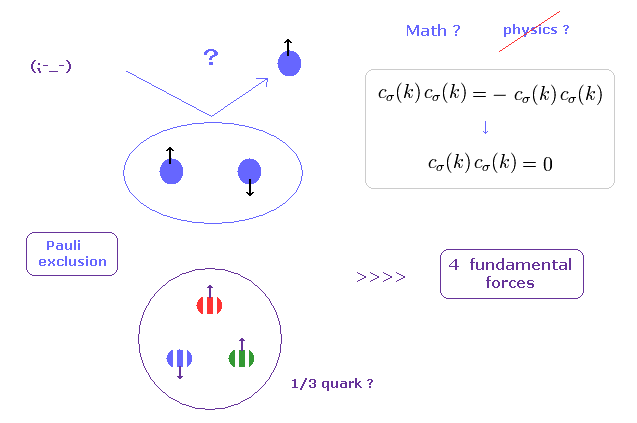
As you see in textbooks of the present condensed matter physics and spintronics, you will find these books are filled with only ( unrealistic ) mathematics, and they NEVER try to ask what spin (= Pauli exclusion principle ) really is.
These "Shut up and calculate !" attitudes of spintronics obstruct the development of science.
In "Pauli exclusion principle", two identical fermions cannot enter in the same place (= state ), even in very strong quarks.
This definition of the "same" place is very vague. How can we define these boundary lines ??
(Eq.4)
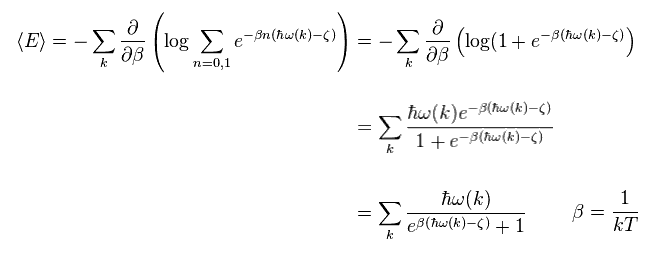
Fermi-Dirac statistics describes distribution of particles in certain systems comprising many identical particles that obey Pauli exclusion principle.
So the particle's number n is "0" or "1".
Like in Eq.1- Eq.3, we get Fermi-Dirac distribution in Eq.4.
Though this Pauli exclusion principle has the greatest power in all fundamental forces, these boundary lines inside which this principle is effective, are very vague. (= These are Only "math" and "symbol" worlds. )
(Eq.5)
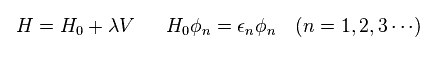
In Eq.5, H0 and ε is the Hamiltonian and its energy in free particles.
"V" is some interactive Hamiltonian.
This V is usually complicated, so they use approximate Hamiltonian H like Eq.5.
(Eq.6)
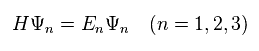
The eigenvalues of this H (= overall Hamiltonian ) is "E", and eigenfunction is "Ψ", like Eq.6.
(Eq.7)
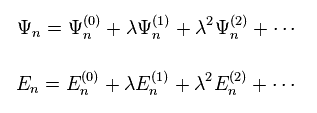
We expand Ψ and E in power of λ, as shown in Eq.7.
Ψ(0) and E(0) are equal to φ and ε of free particles.
Substituting Eq.5 and Eq.7 into Eq.6, we get
(Eq.8)
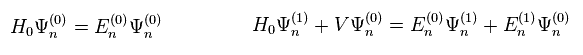
The left of Eq.8 means terms without λ (= zero order ).
We pick up terms which include λ to the power of one in Eq.8 right.
(Eq.9)
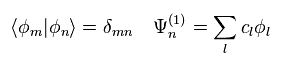
We define each Ψ is composed of (free) eigenfunctions φ of Eq.5, as shown in Eq.9.
And these φ are supposed to be orthonormal.
(Eq.10)
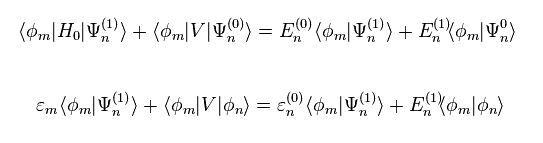
Using Eq.9 in Eq.8 right equation, and multiplying them by φm from the left side, we get Eq.10.
( Eq.5 is used, too. )
When "m" is not equal to "n", the last term of Eq.10 becomes zero.
(Eq.11)
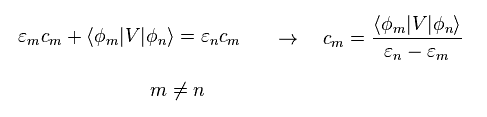
Substituting Eq.11 into Eq.9, we get
(Eq.12)
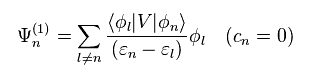
Here "cn" in Ψ(1) is supposed to be zero.
Eq.12 is first-order perturbation.
(Eq.13)
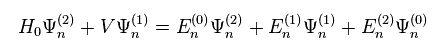
In the same way, we pick up terms which include λ to the power of "2" in Eq.6 and Eq.7.
(Eq.14)
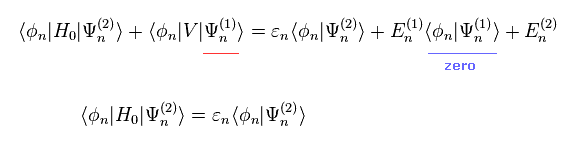
The first terms in both sides are the same, so they can be erased.
Substituting Eq.12 into Eq.14, we get.
(Eq.15)
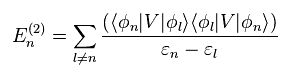
As a result, we get
(Eq.16)
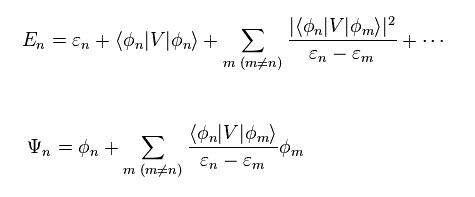
The first order perturbation of E (= second term of right side in the upper equation ) is gotten by multiplying Eq.10 by φn instead of φm.
We often use approximate energy in many-body system in condended matter physics.
So Eq.16 is important.
( This formula is only mathematical thing, which causes divergence. )
Fermi's golden rule means transition rate ( probability ) based on time-dependent Hamiltonian and perturbation.
(Eq.17)
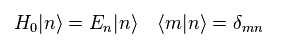
Eq.17 means time independent Hamiltonian and energy of free particle system.
When Hamiltonian includes time dependent interactive part (= H'(t) ), Schrodinger equation becomes
(Eq.18)
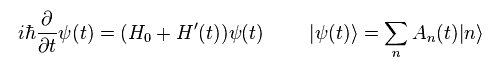
Eq.18 is equal to
(Eq.19)
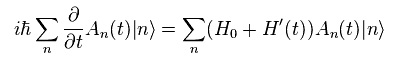
Multiplying Eq.19 by eigenstate "m" from left side,
(Eq.20)
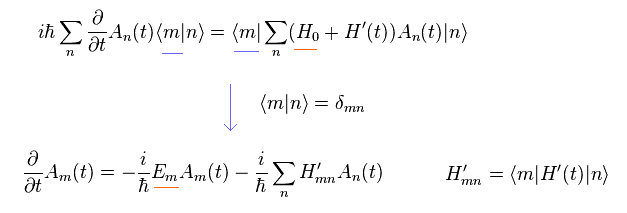
Here we define
(Eq.21)
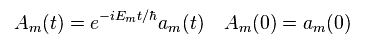
Substituting Eq.21 into Eq.20, and multiplying them by eiEt/h from left side,
(Eq.22)
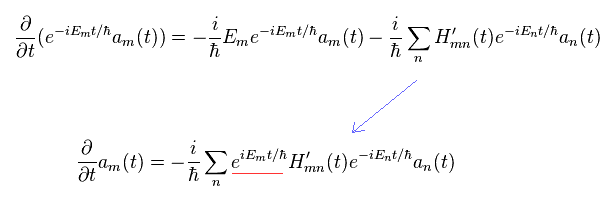
Integrating Eq.22 by t', multiplying them e-iEt/h, and using the relation of Eq.21,
(Eq.23)
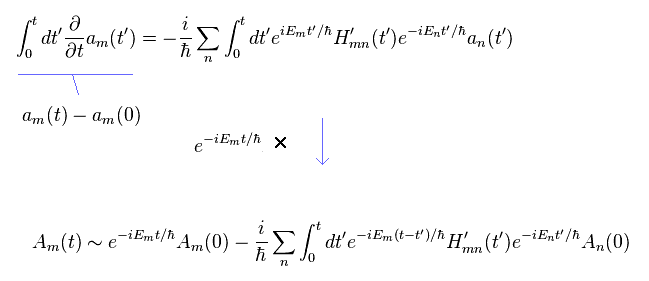
In Eq.23, we approximately change an(t') into An(0) in the right side.
And the following relations are used
(Eq.24)
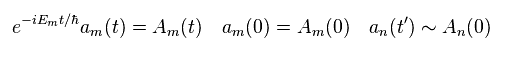
Defining the initial state ( t= 0 ) as a simple form (= δmn ), and picking up only the second term (= interaction ) in the right side of Eq.23,
(Eq.25)
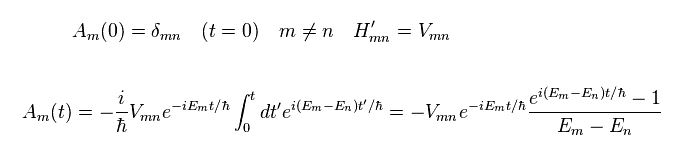
Multiplying Eq.25 by its complex conjugate, we get
(Eq.26)
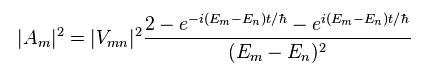
Here we use the following relations,
(Eq.27)
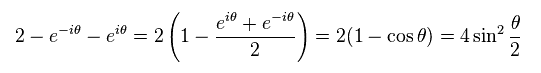
Eq.26 becomes
(Eq.28)
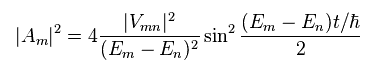
Delta function and its formula are
(Eq.29)
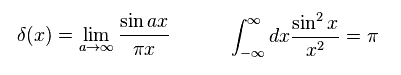
And we define Emn, as follows,
(Eq.30)
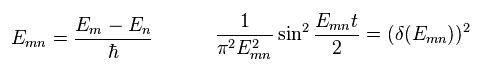
We use the following mathematical trick,
(Eq.31)
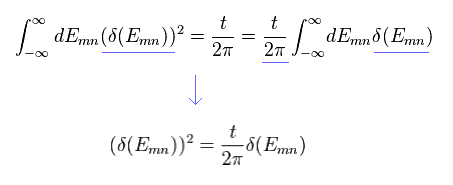
From Eq.28 to Eq.31, we get
(Eq.32)
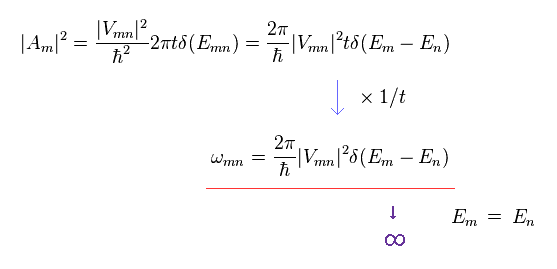
In the first line of Eq.32, using the formula of delta function, "ħ" of Emn inside delta function is erased.
Dividing Eq.32 by time "t", we can get transition rate (= Fermi golden rule ).
The problem is these kinds of transition probabilities are often divergent to infinity due to delta function.
So we should get away from "mathematical" world, and redefine various physical phenomena by "real" objects.
( The same thing can be said about unrealistic "singularity" in the mathematical black hole. )
(Fig.2) How "mathematical" operator can describe various phenomena, rich in variety ??
In the present quantum field theories including condensed matter physics, standard model, and string theory, they completely rely on "mathematical" ( NOT physical ) operators to describe various phenomena.
As you see this page, these creation and annihilation operators do NOT have the power to express various dynamic and complicated phenomena in the actual world.
Because, when a particle is created ( or annihilated ), these operators cannot designate various differernt places and times in each different dynamic particle.
So the main obstructions to the development of sicence are these very abstract oparators (and "spin ") !
(Fig.3) Real variable world is NOT mathematical and simple operators !
As you see various physical phenomena and complicated mechanism in our human bodies, actual particles such as electrons and protons are moving around , interacting with each other at various different places and times.
For example, when a particle A is approching particle B, other another C is getting away from particle D ....
And various interactive "timing" and positional relationship determine various biological functions, which is rich in variety.
Unfortunately, the present mathematical operators such as "a†" and "a" cannot describe these variable functions at all.
(Eq.33)
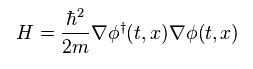
Also in Green's function (= propagator ), these abstract operators are used.
Eq.33 is Schrodinger equation of free particle.
(Eq.34)
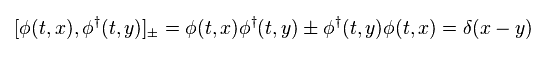
" ± " means anticommutation and commutation relations of eigenfunctions (= operators ).
The eigenfunction in Schrodinger equation is
(Eq.35)
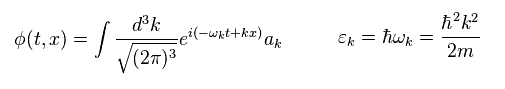
In Eq.35 "k" is wave number, and ħk is equal to a particle's momentum p.
ε means ( kinetic ) energy of a particle.
Substituting Eq.35 into Eq.34, we find "a" and "a†" satisfy the following relation of
(Eq.36)
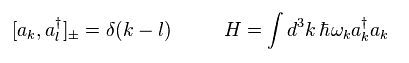
Green's function means the process in which a particle is created at ( t', x' ) and annihilated at ( t, x ) obeying the time order (= T ).
(Eq.37)
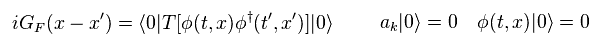
From Eq.35 and Eq.37, this Green function can be expressed using Heaviside step function of
(Eq.38)
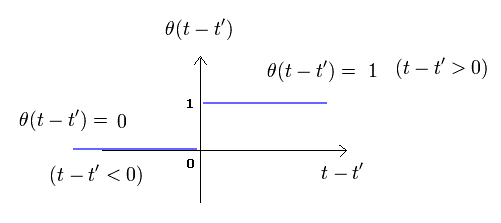
This is used for time-ordered.
In the step function (= θ ) of Eq.38, when (t-t') is positive, θ becomes "1", and when t-t' is negative, θ becomes zero.
(Eq.39)
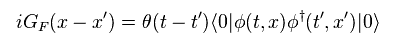
As shonw in this page, using complex integral, step function can be expressed as
(Eq.40)
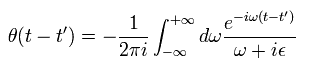
In Eq.40, ε is infinitesimal ( ε → 0 ).
Using Eq.35, Eq.36, Eq.40, Green function of Eq.39 becomes
(Eq.41)
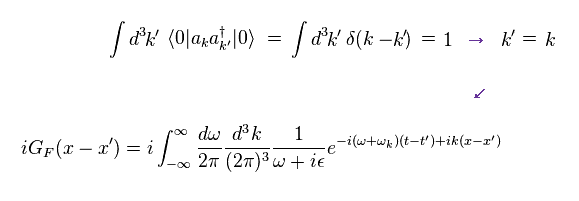
Here we do the replacement of
(Eq.42)
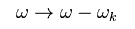
As a result, Eq.41 becomes
(Eq.43)
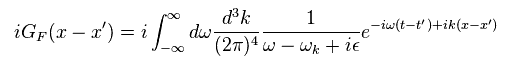
By the definition of delta function,
(Eq.44)
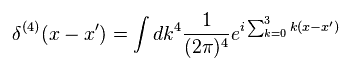
From Eq.35, Eq.43, and Eq.44, we get
(Eq.45)
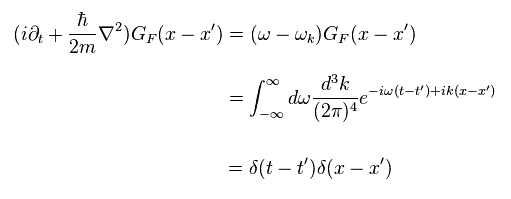
This is Green function (= propagator ) in Schrodinger version.

2013/9/15 updated. Feel free to link to this site.