Top page ( correct Bohr model )
Schrodinger equation is a part of Bohr-Sommerfeld model.
Clear pictures of de Broglie wave and fields. (14/10/22)
In 1923, Louis de Broglie's suggested "de Broglie's waves", which was experimentally confirmed by Davisson and Germer in 1927.
The de Broglie's relation has been confirmed in various particles such as electrons, neutrons, and atoms..
(Of course, also in the electromagnetic waves.)
And de Broglie's wavelength (λ) is influenced only by the momentum ( p = mv ).
This means that the fields which causes de Broglie's waves senses the particle's momentum ( not its velocity).
Because various particles of different masses have different velocities, though their momentums are the same.
λ = h / p = h / mv
As shown in this page, we have "mathematically" proved that the Schrodinger equation also uses the idea of an integer times de Broglie's wavelength and it is only an special version of Bohr-Sommerfeld model.
And furthermore, we have explained the reason why the Schrodinger equation is wrong.
By the way, what on earth is de Broglie's wave ?
Can we express the de Broglie's waves by the classical waves ?
In this page, we try this thing.

In this page, we divide the electron's momentum into two directions ("tangential" and "radial").
The de Broglie's wavelength is inversely proportional to the momentum.
Can we divide the de Brgolie's waves into two directions correctly to satisfy the de Broglie's relation ?
(Fig.1) Dividing de Broglie's wave into two directions.
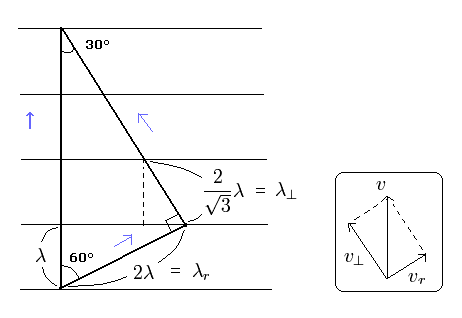
First, we consider the case of Fig.1.
In Fig.1, the wavelength in the moving direction is λ.
And each wavelength of "tangential" and "radial" directions becomes as shown in Fig.1.
By the way, these wavelengths satisfy the Pythagorean theorem in the above three momentums ?
(Eq.1) Pythagorean theorem + the de Broglie's relation.
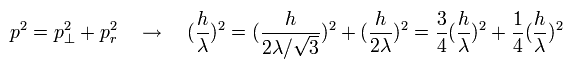
As shown in Eq.1, these de Broglie's wavelengths satisfy the Pythagorean theorem correctly !
This means that the de Broglie's wave is just equal to the "classical" wave.
The wave phase can be expressed as
(Eq.1-2)
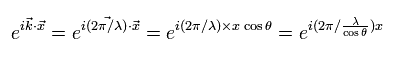
where θ means the angle between the vector x and the wave moving directions (k).
Eq.1-2 means that if the angle θ changes from zero to θ, the wavelength of λ changes as follows,
(Eq.1-3)
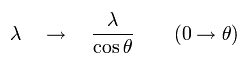
So when the vector x doesn't point to the wave moving direction (k), the wavelength in the x direction becomes longer than λ !
We can generalize this model using an arbitrary angle of θ (Fig.2).
(Fig.2) Arbitrary angle of θ.
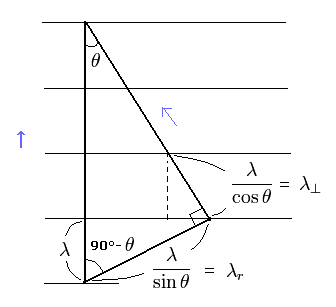
Fig.2 satisfies the next Pythagorean theorem in the momentums.
(Eq.2)
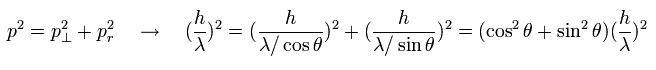
We have proved that de Broglie's waves are similar to "classical" waves.
We can prove this thing by another method (Fig.3).
(Fig.3) Interference of two crossing waves.
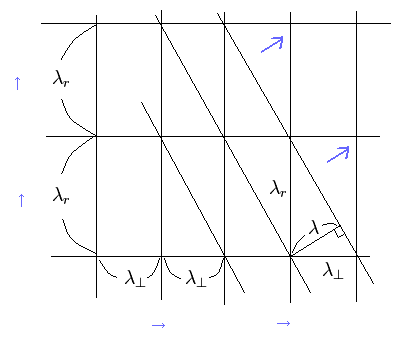
In Fig.3, the two waves in tangential and radial directions are crossing each other.
The oblique lines connect the points at which the wave amplitudes are bigger (mountain + mountain, or valley + valley).
If we consider that the distance between these two oblique lines is the new wave's length λ, it satisfies,
(Eq.3)
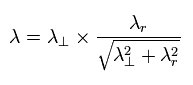
And we can prove that these wavelengths satisfy the momentum's Pythagorean theorem using de Broglie's relation, as follows,
(Eq.4)
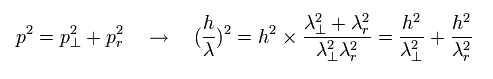
As shown in this page, in the Bohr-Sommerfeld theory, we use the Sommerfeld's conditions in which both the tangential and radial de Broglie's waves need to be intergers in one orbit (= 2π rotation).
We try to visualize these Sommerfeld's conditions concretely.
Considering the Bohr model hydrogen's ground state and the result of the interference experiment, it is thought that there is only one space in one de Broglie's wavelength, as follows,
(Fig.4)
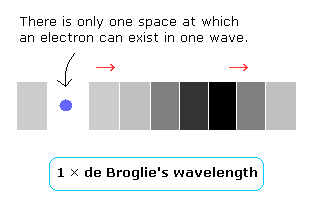
And this electron's space (= wave phase) is moving according to the electron's velocity, because an electron can exist only at one space (=phase) in one wave.
(Fig.5)
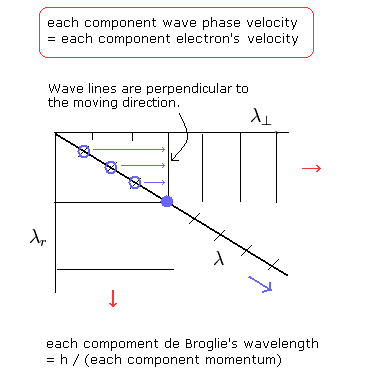
As shown in Fig.5, the phase velocities of each component (tangential and radial) are thought to be equal to the electron's velocities of each component.
So the tangential wave phase lines are perpendicular to the tangential direction.
In the hydrogen atom, the angular momentum (L) is
(Eq.5)
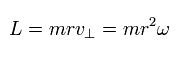
This L is constant in the hydrogen's elliptical orbit.
As I said above, de Broglie's wavelength is related only to the momentum, so the tangential de Broglie's wavelength is
(Eq.6)
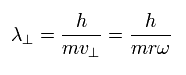
Here we consider a sector with the central angle of θ1.
The arc length of this sector is r × θ1. ( r is the radius. )
(If this θ is very small, the radius r can be considered to be constant in an elliptical orbit.)
So the number of de Broglie's waves (n) contained in the small arc is
(Eq.7)
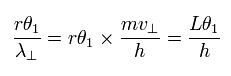
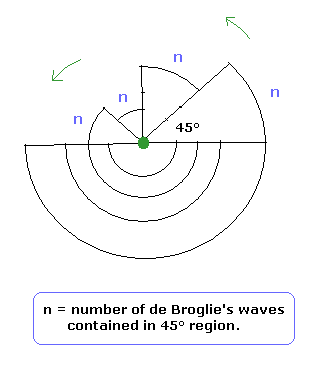
This means that irrespective of the radius r length, the same "tangential" de Broglie's waves (= n ) are contained in the arc which has the same central angle. (For example, Fig.6 is the case of 45 degrees.)
(When L is ħ, one orbit (θ=2π) contains 1 × de Broglie's wave. Try substituting this into Eq.7.)
If the "tangential" wave phases return to the original states, the angular momentum (L) of Eq.7 must be an integer times ħ.
(Fig.6) Irrespective of the r, de Broglie's waves become the same (= n) in each arc.
By the way, can we divide the tangential (= θ) wave into two more directions ? (like a1 and a2 directions of Fig.7B.)
And can we consider each orbit of the a1 and a2 directions contains an integer times de Broglie's waves like the tangential direction ?
(Fig.7)
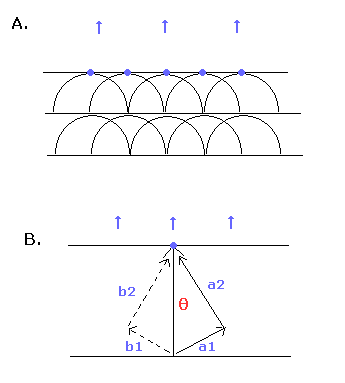
According to the Huygens-Fresnel principle, each point of a media (disturbed by passing wave) acts as a point source (Fig.7A).
So the waves in the a1 and a2 directions interfere with the "symmetrical" waves of b1 and b2 (Fig.7B).
As a result, only the tangential direction (θ) is left.
So we don't need to divide the tangential wave into more directions.
Basically, the shortest wave is left according to Huygens principle. (Fig.7A.)
In the hydrogen atom, the orbit is closed.
So when we consider the wave phases after 2π rotation, only the orbit of the shortest length (= tangential direction) needs to be considered.
(Of course, we also need to consider "radial" direction, which doesn't contribute to the rotation.)
As shown in this page, if we consider these de Broglie's waves and the electromagnetic waves, we can explain the photoelectric effect and the discrete energy levels "naturally".
Suppose the light source emits the electromagnetic waves or photons to the universe. (Fig.8).
(Fig.8)
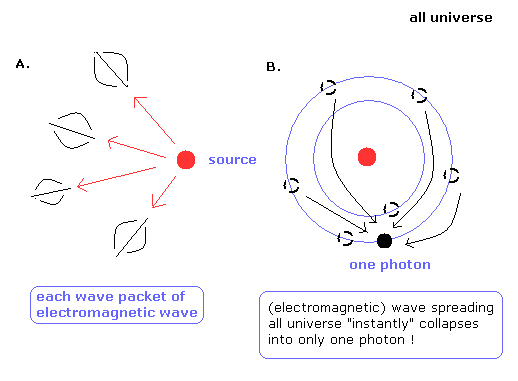
It is very unnatural that the electromagnetic waves are spreading into the universe equally and endlessly.
It is natural that the electromagnetic waves emitted by the sourse are a little unequally distributed, which becomes more conspicuous as they spread over more area.
It travels through the space as a wave packet. (Fig.8A.)
As a result, we can detect each wave packets of the electromagnetic waves from the universe.
How about the photon particle ?
According to the quantum mechanics, the probability waves (= electromagnetic waves) of a single photon are spreading into the universe equally and endlessly.
And when we detect the photon particle at some point, the electromagnetic waves in all space "instantly" collapse into only one photon ! (Fig. 8B.)
So this photon model can not be acceptable, and the electromagnetic wave model of Fig.8A is thought to be more natural.
In the Bohr model hydrogen, the ground state orbit is one de Broglie's wavelength, as follows,
(Eq.8)
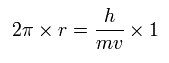
And in this orbit, the electron's frequency can be expressed as velocity / orbital length, as follows, (using Eq.8)
(Eq.9)
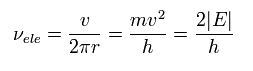
where we use the next relation,
(Eq.10)
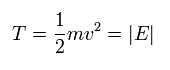
In the hydrogen's circular orbit, the kinetic energy (T) is equal to the absolute value of the total energy (E).
In the photoelectric effect, when we illuminate the hydrogen atom by the electromagnetic wave with the energy of
(Eq.11)
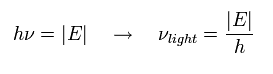
the electron is emitted from the hydrogen atom.
The electron's frequency (Eq.9) is just twice the light frequency (Eq.11).
Considering the fact that the electron's kinetic energy (T) also contributes to the photoelectric effect, this result is acceptable.
If we try to keep the original electron's velocity in the emitted electron, the necessary light frequency becomes
(Eq.12)
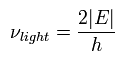
Eq.12 is just equal to Eq.9 !
So the electromagnetic wave vibrates the electron's motion. (Their cycles are the same in Eq.12.)
The result of Eq.9 and Eq.11 (Eq.12) means that the Planck's constant (h) in the photoelectric effect is related to the de Broglie's wave !
So it is very natural that we think the photoelectric effect is caused by the electromagnetic wave and de Broglie's wave.
About the photoelectric effect by the electromagnetic wave, see also this page.
--------------------------------------
If we solve the usual Maxwell's equations, we can get the next relations.
(Eq. M-1)
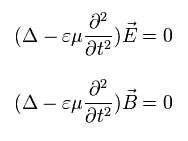
where the following relations are satisfied.
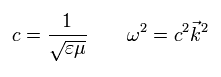
From the above equations, we can get the solutions of electromagnetic waves "naturally" (Eq.13).
For example, the electromagnetic wave which travels in the z direction is composed of the changing electric field (E) and magnetic field (B) of
(Eq.13)
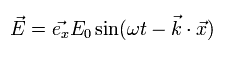
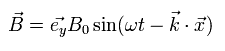
Eq.13 are solutions of the above equations of Eq.M-1.
As shown in Eq.13, the amplitudes of E and B in the original electromagnetic waves are not attenuated at all.
But if we consider the old equations of the accelerated charge, the amplitude of the electromagnetic waves are attenuated, as follows,
(Eq. M-2)

where p means the electric dipole.
And the "accelerated" dipole (p) radiates the electromagnetic wave in Eq.M-2
As the distance (= r) between this dipole and a point beomes longer, the amplitude of E and B becomes weaker as shown in Eq.M-2.
Why is this result of Eq.M-2 different from Eq.13 ?
The important point is that Eq.M-2 doesn't use the concept of de Broglie's waves at all !
Though every moving particle causes de Broglie's waves, why does Eq.M-2 neglect this thing ??
This is the reason why we misunderstand about the electromagnetic waves.
Especially in the atoms, we have to think about the quantization of de Broglie's waves !
If so, the electromagnetic wave (packet) is a little unequaly emitted, and not attenuated as shown in Eq.13.
In the old classical Maxwell equation, the energy density (u) of this electromagnetic wave is expressed as
(Eq.14)
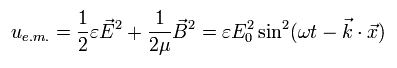
But the energy density equation of Eq.14 has some defects.
According to Eq.14, the angular frequency (ω) doesn't contribute to the energy at all. (at the atomic level.)
Even if we change the angular frequency of Eq.14 as follows, the total energy doesn't change at all !
(Eq.15)
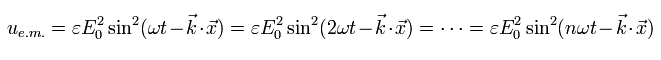
[ These energies of the electromagnetic waves are the same ?? ]
where the upper electron is swaying very slowly, and the lower electron is vibrating very vigorously.
And they have the same amplitude.
According to the interpretation of Eq.15, these energies of the electromagnetic waves are completely the same !
It is irrational.
This means the energy density of Eq.15 is incomplete.
So we need to improve the old idea about the photoelectric effect.
Basically, the frequency itself is clearly wave's nature ! ( It is not a particle's nature .)
It is quite natural.
And if we consider the frequency in the electromagnetic waves, we don't need to use the concept of photons at all.
As you know, de Broglie's waves of electron interfere with itself and it influences the electron's movement direction.
So it is natural that we think there are two different places (phases) where an electron can and can't exist in one de Broglie's wave.
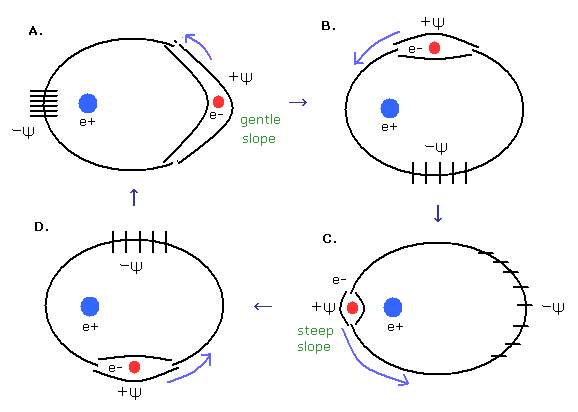
Here we define the phase where an electron can exist as Ψ +. ( The opposite phase where the electron can't exist is defined as Ψ - .)
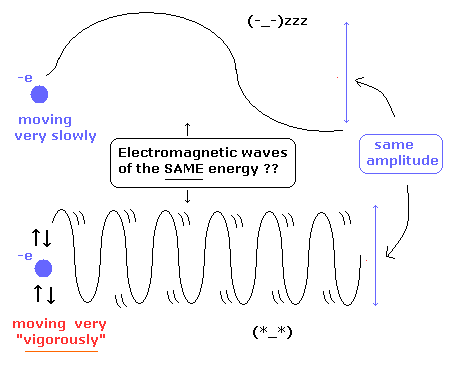
(Fig.9) Short (= A. ) and long (= B. ) de Broglie's wavelengths.
The direction of the electron's movement agrees with that of de Broglie's wave phase change.
So it is natural that we think de Broglie's waves as "longitudinal" waves.
Fig.9A. means "short" de Broglie's wavelength, so the electron's momentum (= velocity) is large in this case. ( λ = h/mv. )
In Fig.9A, a pair of hill (= +Ψ ) and valley (= -Ψ ) is packed in a short segment.
So the slope is steep (= the "imbalance" of medium densities is big ), and the electron moves faster than Fig.9B (= "long" de Broglie's wavelength.)
As the imbalance of the medium becomes smaller (= Fig.9B), the force which pushes the electron becomes weaker, then the electron becomes slower.
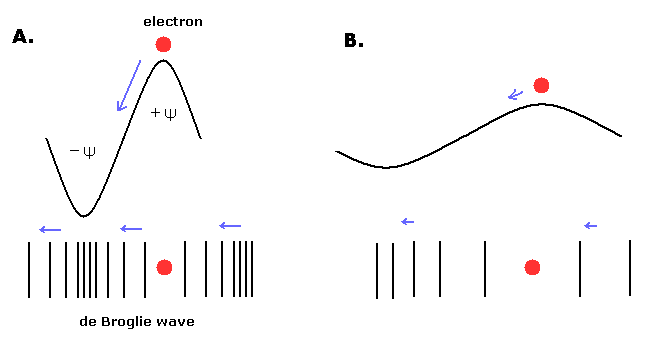
(Fig.10) 1 × de Broglie's wave in hydrogen's "circular" orbit.
Fig.10 expresses the 1S circular orbit of the hydrogen atom, in which the orbital length is 1 times de Broglie's wavelength.
In the circular orbit, the electron's momentum (= velocity) is constant in any point of the orbit.
So the phase velocity of de Broglie's wave is constant as shown in Fig.10 ( A. → B. → C. → D. → A. )
(Fig.11) de Broglie's waves in "elliptical" orbit.
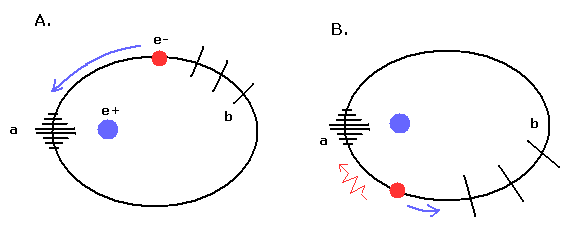
In the "elliptical" orbit like Fig,11, it is a little complicated.
In Fig.11, the point "a" is perihelion.
In Fig.11A, the electron is approaching the perihelion "a".
So in this state of Fig.11A, the electron is accelerated (= becomes faster), which "wrinkles" and condenses the field around perihelion.
In Fig.11B, the electron is going away from the perihelion, and is decelerated.
So also in this state of Fig.11B, the field around the perihelion (= "a" ) tends to be wrinkled due to the electron's brake.
As a result, around perihelion (= "a" ), the fields tends to be condensed and wrinked, which leads to "short" de Broglie's wavelength.
On the other hand, around aphelion (= "b" ), the field tends to be extended, which leads to "long" de Broglie's wavelength.
While the electron is passing the perihelion, its speed becomes faster due to the steep slope of de field phase.
(The space Ψ+ where the electron can exist is basically "empty" space, because the electron pushes the medium toward Ψ -. )
(Eq.16) Phase speed (= v ).
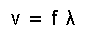
Eq.16 means the phase speed, where f is the frequency and λ is the wavelength.
In the region of the short de Broglie's wavelength, f becomes bigger due to the condensed and wrinkled fields.
(Imagine the frequency f is related to the spring constant "k". )
But of course, the overall frequencies (of one-round orbit) in all points need to be equal.
The point is that only when the electron is passing, the "temporary" frequencies are different in the different wavelength regions.
When the electron is passing the aphelion (= "b" ), its speed becomes slower due to the "loose" fields, which slow electron affects the opposite position "a".
So in this state (= the electron is passing "b" ), the phase speed around "a" is slow, too.
(Around perihelion "a", the fields tends to be condensed. )
On the other hand, when the electron is passing the perihelion "a", its speed becomes fast due to the "steep" phase.
In this state, the phase speed around "b" is fast, too.
Because the field around "b" tends to be diluted.
As a result, the overall frequencies become equal in all points also in the elliptical orbit.
(Fig.12) Phase change of elliptical orbit.
According to de Broglie's theory, de Broglie wavelength λ is dependent on the particle's momentum (p).
( λ = h / p )
Here we think about accelerating the electron until it reaches the momentum p under electric fields.
(Fig.13) Accelerating electron.
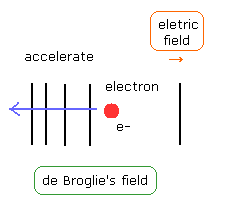
As the electron becomes faster under the electric field, de Broglie's wavelength becomes shorter as shown in Fig.13.
Of course, during this process, de Broglie's fields around the electron is unstable, which are "twisted" by the accelerated electron under the external force (= electric field).
After the electron gets to the constant momentum p, it becomes free electron and stable without the external force. (Fig.14)
(Fig.14) Free electron with constant velocity.
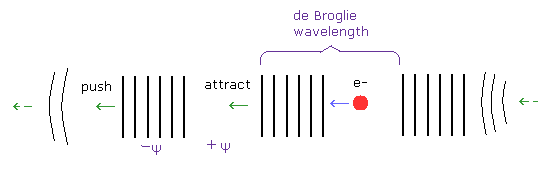
In the free electron, its de Broglie wavelength is constant and stable.
The distortion of the fields (= wavelength ) becomes a motive force of the particle's momentum.
The phase -Ψ (= "condensed" field ) pushes the front fields, which becomes new -Ψ phases.
On the other hand, +Ψ phase (= "diluted" field ) attract the rear -Ψ phases. ( Both strengths are the same.)
In this way, de Broglie wave of free electron goes forward keeping constant de Broglie wavelength.
(The electron's momentum and de Broglie fields around it harmonize with each other, so both of them are stable.)
(Fig.15) Same momentums, but different velocities.
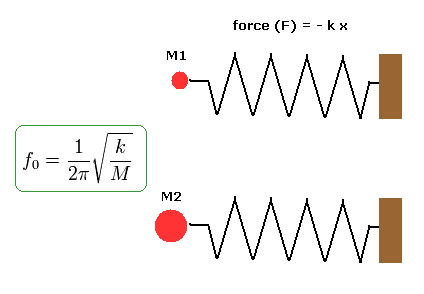
For example, the electron and neutron have different masses ( ex. m = M1 or M2 ).
So when they have the same momentum ( p = mv ), their velocities (= v ) are different.
Here we explain this mechanism using an example of a spring, as shown in Fig.15.
In Fig.15, the upper and lower springs have the same spring constant k and amplitudes.
So the forces ( F = - kx ) which pushes the particles and the spring energy (= 1/2 kx2 ) are the same in them.
But the masses of the particles which stick to the springs are different. ( upper particle = M1, lower particle= M2 ).
In this case, the frequencies ( f0 ) and phase velocities are different in them, though they have the same spring energy.
(As the mass becomes heavier, its velocity becomes slower.)
Of course, this distortion of the spring (= spring energy) is conserved.
So we can consider this distortion of the spring as a thing like the distortion of de Broglie fields (= wavelength).
(Fig.15') Circular and elliptical orbits.
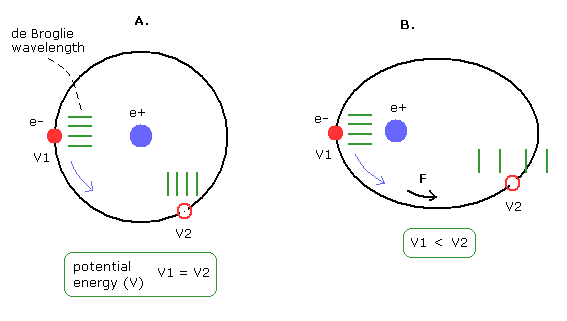
In the circular orbit of Fig.15' A, the potential energies (V) are the same in all points.
So the "extra" force is not needed for the electron to move.
As a result, the electron's "effective" mass is conserved, and the phase speed is constant.
But in the elliptical orbit like Fig.15' B, the potential energies changes according to the electron's positions.
So the "extra" force is needed for the electron to move.
We can consider this case as the electron's "effective" mass change ( V1 → V2, M1 → M2 ).
(For example, as the potential energies becomes higher, the "effective" mass becomes heavier. )
Then, the phase speed is changing continuously. (See Fig.15)
(Fig.16) Wavelength (= "distortion" ) of de Broglie fields is conserved in each point.
When the wavelength at some point of the elliptical orbit is λ, it is natural that we think its wavelength is conserved at the point.
After the electron with the momentum p passes this point ( λ = h/p ), the diluted phase +Ψ attract the phase -Ψ with the same wavelength, because the "spring energy" at the point is conserved.
If the de Broglie wavelength is NOT conserved after the electron has passed the point, it causes serious problems.
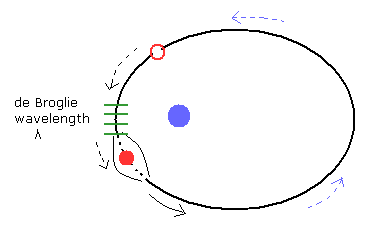
(Fig.17) The electron's motion becomes "unstable" emitting de Broglie waves.
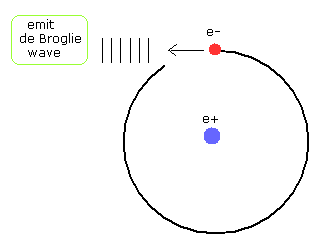
In Fig.17, the de Broglie's wavelength is NOT conserved at each point of the orbit.
When the electron with the momentum p comes into this point , it needs to cause de Broglie's wavelength λ (= h/p ) at this point.
( The electron "pushes" and wrinkles the front field. )
But its direction of the de Broglie wave is "tangential", so this de Broglie's waves are emitted in the tangential direction.
As a result, de Broglie waves (= field energies ) are not conserved, which makes the electron's motion unstable.
(So this case doesn't occur in usual atoms.)
(Fig.18) Distortion of de Broglie's fields is conserved at each point.
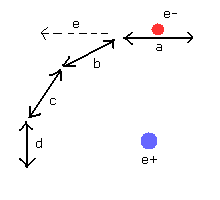
As shown in Fig.18, de Broglie wavelength at each point of the orbit is conserved in both the wavelength and direction.
In this state, the electron with changing momentum (in the direction and speed ) can go forward to the next field smoothly, hamonizing with de Broglie fields.
If the "b" field of Fig.18 does NOT exist, when the electron at the point "a" comes into "b", the de Broglie wave at "a" goes away in the direction of "e".
So for de Broglie fields to be stable, de Broglie field at "b" need to induce "a" field de Broglie waves in the direction of "b".
And if de Broglie waves are emitted in "e" direction, these de Broglie waves at "e" and "b" interfere with each other.
(Of course, they have different (momentum) directions, this inteference makes "b" field wavelength unstable.)
As a result, for de Broglie fields to be stable, de Broglie field of "b" with proper wavelength and direction is conserved and prepared in advance.
(Fig.19) An integer times de Broglie wavelength needs to be conserved.
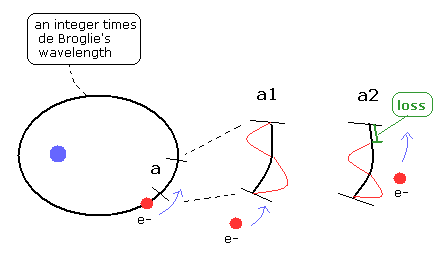
As you know, de Broglie waves of the electron interfere with each other.
So the phase ends of them need to agree with each other to prevent canceling each other.
This means one round orbit needs to be an integer times de Broglie wavelength.
If de Broglie wavelength at each point is not conserved, the serious problem occur.
For example, there is a field with some de Broglie wavelength at the region "a" in the orbit at a point of time.
We suppose this de Broglie wavelength is different from the electron's momentum which passes this region. ( a1 of Fig.19 )
And at this moment, one round orbit contains an interger times de Broglie's wavelength for the wave itself to exist, as I said above.
When the electron comes into this region of "a", the de Broglie's wavelength of this region needs to be the same as the electron's momentum ( a2 of Fig.19 ).
But here we suppose de Broglie wavelength existing in advance is different from the electron's momentum when the electron doesn't exist in region "a".
So the number of de Broglie waves included in this region "a" changes, as shown in a2 of Fig.19.
This is contrary to the first condition of an integer times de Broglie wavelength, and the wave becomes unstable.
As a result, the de Broglie wavelength at each point needs to be conserved even after the electron goes past.

2011/3/6 updated. Feel free to link to this site.