行列
|
|
【連載 面積(#11)】において、球の上半分の表面積 Su は 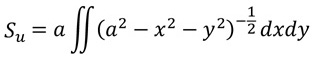 で与えられ、これを計算するために極座標変換すれば良いことを述べました。 結論から先に書いておきましょう! とおくと、  となります。積分区間が2種類ありますが、1つは動径rに関するもので、 今は、原点を中心とする半径aの球を考えているので、積分区間が [0, a] となります。 もう1つは偏角θに関するもので、グルッと1周分積分するので、積分区間が [0, 2π] となっています。 小括弧内は大丈夫でしょうかね。 なので、このように変換されます。 問題は、最後の部分です。 今、2変数(x、y)を、2変数(r、θ)で変換しているのですが、 「dxdy」が「drdθ」ではなく、「rdrdθ」になっています。「r」が余計についています。 これは、どうしてでしょうか? 実は、この部分を理解するために「行列」という1つの単元を学ばないといけません。 大学1年生で学ぶ内容です。 「行列」と言っても、“人気のラーメン店に2時間待ちの行列ができました!”とか、 “アリの行列”などではありません。 数を長方形状に並べたものです。例えば、 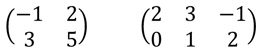 行列の計算は、足し算は予想通りの計算ですが、掛け算が意表をついた計算です。 例えば、次の2つの行列  に対して、まず、足し算をしてみると、 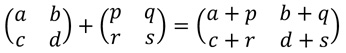 これは、ある程度想定内でしょう。同じ成分どうしを足し合わせています。 しかし、掛け算をしてみると、  となります。これには「えっ?」と思うのではないでしょうか?・・・詳しくは授業にて♪ 次回は、行列と面積の関係について見ていきたいと思います。 |
|
|