方程式の解を求める
数式処理言語(「Mathematica」や「Maple」など)を用いれば,方程式 f(x) = 0 の解は,プログラムを書かなくても簡単に会話的に求めることができるが,科学技術計算においては大がかりなプログラムの中で繰り返し,解を必要とすることがあるから,基本的なプログラム技法を知っておかなければならない。
(1) 単純な繰り返し法
方程式を x = F(x) の形に書き換えたときに,解 x = s における微係数 F’(s) が,|F’(s)|<1 を満たしているならば,適当な初期値 x(0) を選べば,漸化式
x(n+1) = F(x(n))
は n→∞ で収束し,その極限値が求める解となる。
(説明)x〜s の近傍で漸化式は
x(n+1) - s 〜 F'(s) (x(n) - s)
すなわち真の解からの差は、公比 F'(s) の等比数列で近似される。
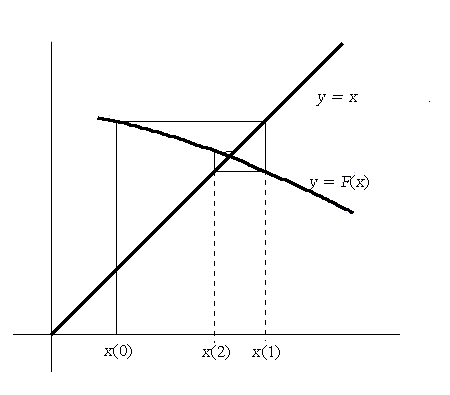
プログラムでは単に以下のように書いて,適当な初期値と終了判断を与えて繰り返すだけでよい。:
x = F(x)
公比 r の等比数列なら、極限値との差が
x(n) - s = [x(n+1) - x(n)] / (1 - r)
をみたすことを用いれば、終了条件を決めるのは簡単であろう。F(x) が簡単な式で書けるものなら関数電卓でも計算可能であるから,収束の様子を見るために試してみよう。
問1 x - cos(x) = 0 をみたす実数 x の値を電卓で求めよ。答え 問2 『方程式 m = tanh(m/T) は T<1 のとき,m≠0 の解を持つ。T と m の関係を グラフで描け。』と言われたらどうするか? tanh は双曲正接関数で,指数関数 で書けば,tanh(x) = sinh(x)/cosh(x) = [exp(x)-exp(-x)]/[exp(x)+exp(-x)] である。x = 0 で値が 0,傾き1で単調に増加し, x→±∞ で±1に近づく。答え
(2) 二分法(はさみうち法)
最も簡単で確実な方法である。あらかじめ概形をグラフに描くなどより、関数 f(x) が x = a と x = b の間で1回だけ符号を変えることがわかっているとする。手続きはどちらでも同じであるから、図のように
f(a)<0 , f(b)>0
であるとする:
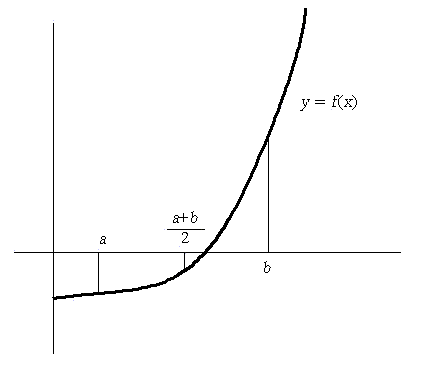
f(a)<0,f(b)>0 をみたす a,b の初期値を与えておく。
d = 求めたい精度(誤差)を与えておく
・・・・・・・・・・・・・・・・・・・・・
ent: IF |b-a|≦ d なら exit へ
x = (a+b)/2.0
y = f(x) を計算する。
IF y>0 → 新たに b = x として ent へ戻る
ELSE IF y<0 → 新たに a = x として ent へ戻る
・・・・・・・・・・・・・・・・・・・・・
exit: x が求める解である。
精度(誤差) d の値を予め設定しておく必要があるが、これをシステムで用意されている実数の精度より小さくすると、exit条件が永久に成り立たず終了できないことがある。幅が半分、半分と縮められていくから、何回くらいの繰り返しが必要か、予め予想することができよう。この方法は、数値や文字列データの配列要素を大きさ順(アルファベット順)に並べ替える作業(Sorting)にも応用できる。データ量が大量の場合には、端から順番に調べるよりはるかに速くなることがわかるだろう。
(3) ニュートン法
解を確実に得ることができるという点では不安があるが、関数のグラフが解の付近で図のように単調になっていることがわかっている場合には、曲線の勾配を利用すれば更に効率的になる。
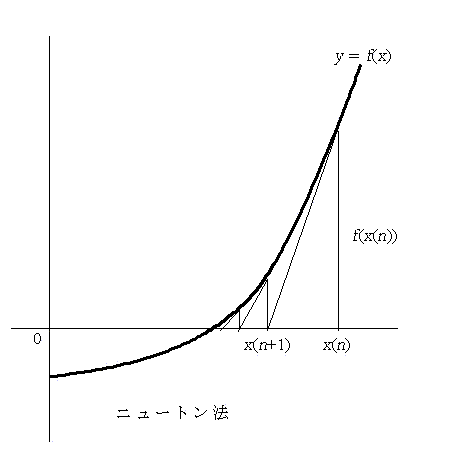
点 ( x(n), f(x(n) ) におけるグラフの接線
y - f(x(n)) = f'(x(n)) ( x - x(n) )
が x 軸と交わる点を、次の x(n+1) とする。すなわち
x(n+1) = x(n) - [f(x(n))/f'(x(n))]
同じように、精度 e を与えておき
|x(n+1)-x(n)|/x(n+1) ≦ e
でもって終了条件とすればよい。
もちろん導関数は数値的に求めるのではなく、その関数形が予め分かっているものとする。この方法がなぜ速いのかについては図を見れば一目瞭然であるが、真の解 s からの誤差 x(n) - s が、先の二つの方法のような等比数列ではなく、ベキ数列
x(n+1) - s 〜 [f"(s)/2f'(s)] ( x(n) - s )2
で減少することを示すことができる。(注) 詳しいことについては早川先生のノート「第3講」参照。また、解が重解になる場合、すなわち、f(x) のグラフが x 軸と接する場合には、収束が遅くなるが解は求まることも理解できよう。
問3 ニュートン法で正の実数の平方根を求めるにはどうすればよいか? 答え
精度を予め与えるのではなく、10ないし20回繰り返して、何回くらいで有効数字6桁の範囲で知っている平方根の値に到達するか、確認してみよ。初期値は x = r で十分であろう。次に倍精度で実行してみよ。 [√2 = 1.41421356..., √3 =1.7320504... , √5 = 2.2360679... など]
これに対して重解の場合、例えば f(x) = x2 の場合、f’(x) = 2x で、漸化式は
x(n+1) = x(n) - x(n)2/2x(n) = x(n)/2
となり、明らかに解0に向かって等比数列的にしか収束しない。(それでも十分に速いが)第二回課題
ソースプログラムと見やすくデザインされた出力結果を一つのファイルにまとめてemailで提出するか、紙に印刷して提出すること。
・ 次の漸化式で作られる多項式を「ルジャンドル多項式」という。
Pn(X) = (2 - 1/n) X Pn-1(X) - (1 - 1/n) Pn-2(X)
P0(X) = 1 , P1(X)= X
(特徴)
n が偶数なら偶関数 Pn(-X) = Pn(X)
n が奇数なら奇関数 Pn(-X) = -Pn(X)
Pn(1) = 1 for all n
P2n(0) は (-1)n と同符号
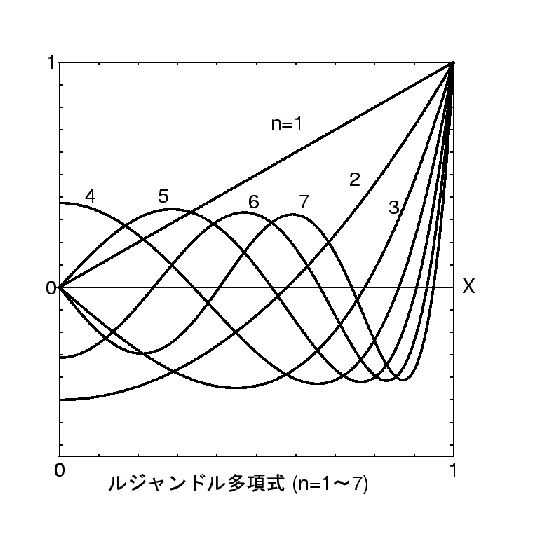
Pn(X) はn次の多項式で、(-1,1) 間にn個のゼロ点[ Pn(x)=0 となる x ]を持つ。このn個のゼロ点は、Pn-1(x) のn-1個のゼロ点と -1 および 1 をあわせて並べた n+1 個の点の間に一つずつ挟まれている。n=2 から n=10 まで順番にゼロ点(対称性から、正のものだけでよい)を、小数点以下5桁の精度で求めよ。
(ヒント)予め漸化式を用いて多項式の各項の定数係数を求めておく方がよい。『整数/整数』 に注意!