機械工学実験室

１．材料力学実験

１．１　梁のたわみ実験
両端支持はりの撓みを測定し、計算値との比較をする。
１）実験条件
　・梁のスパン　４００ｍｍ
　・梁の断面形状　幅１０ｍｍ、厚さ２ｍｍ
　・梁の材料　SUS、アルミニウム
　・荷重　1N～10Nまで1Nきざみで錘を梁の中心(点C)に吊るし撓みを測定

２）梁の撓み式　

　　撓みδ＝W*L＾３/（48*E*I)

　　　　　　ただし、E：ヤング率
　　　　　　　　　　　I：断面2次モーメント
　　　　　　　　　　　L：A～B間の距離400mm

３）結果
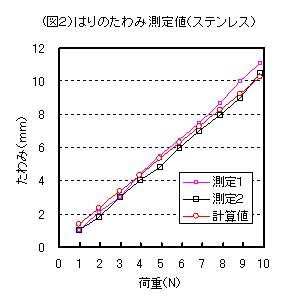
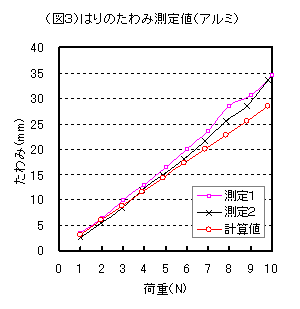
　（図２）、（図３）に計算値（赤線）と測定値を示す。
SUS材の場合計算値に対し測定値は最大誤差10%以内にあります。
AL材の場合７N以上において測定値の誤差が拡大していますが、これ
は材料に発生した応力が耐力を超え線形性が失われたためと考えます。

以上のように、梁の撓み計算式は実測値と良く合う事がわかります。
このような計算式を確立した先人の努力に敬意をはらいます。
















2. 伝熱工学実験

2.1 アルミ円柱からの放熱実験
　　　　　　　
1)実験条件
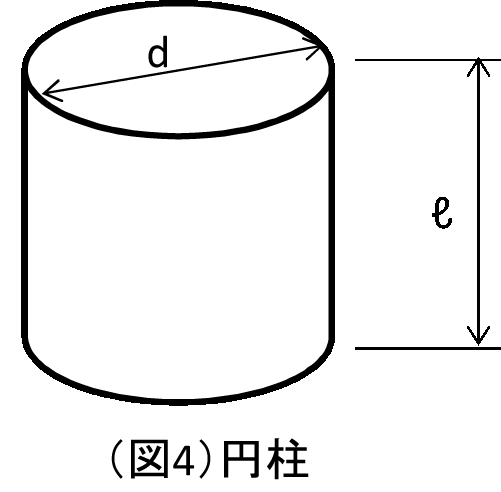
（図4）に示す円柱を温水（約80℃）の中に入れ、（図4）の円柱中心部まで均等に加熱されて
いることを確認し、大気中へ出し円柱の側面と中心部温度を計測した。
この計測値と有限要素法（2次元）と放熱論理式の景観結果を比較してみた。
円柱の寸法はφ30×30ℓである。


２）放熱のメカニズム
　円柱は0.4ｍｍの細い針金を取り付け、常温（28℃）室内空気中に放置した（図６）。室内に空気の流れはないため、円柱表面からの　自然対流熱伝達と放射熱伝達による熱伝達が放熱メカニズムと考えられる。
　ただし、等価放射熱伝達率は計算したところ自然対流熱伝達率に比べ2桁小さいため無視する。


3）放熱の微分方程式
　Cdt＝－ｈ（t-ta）Aｄτ
　この式を解きτ＝0でｔ＝tiの条件を入れると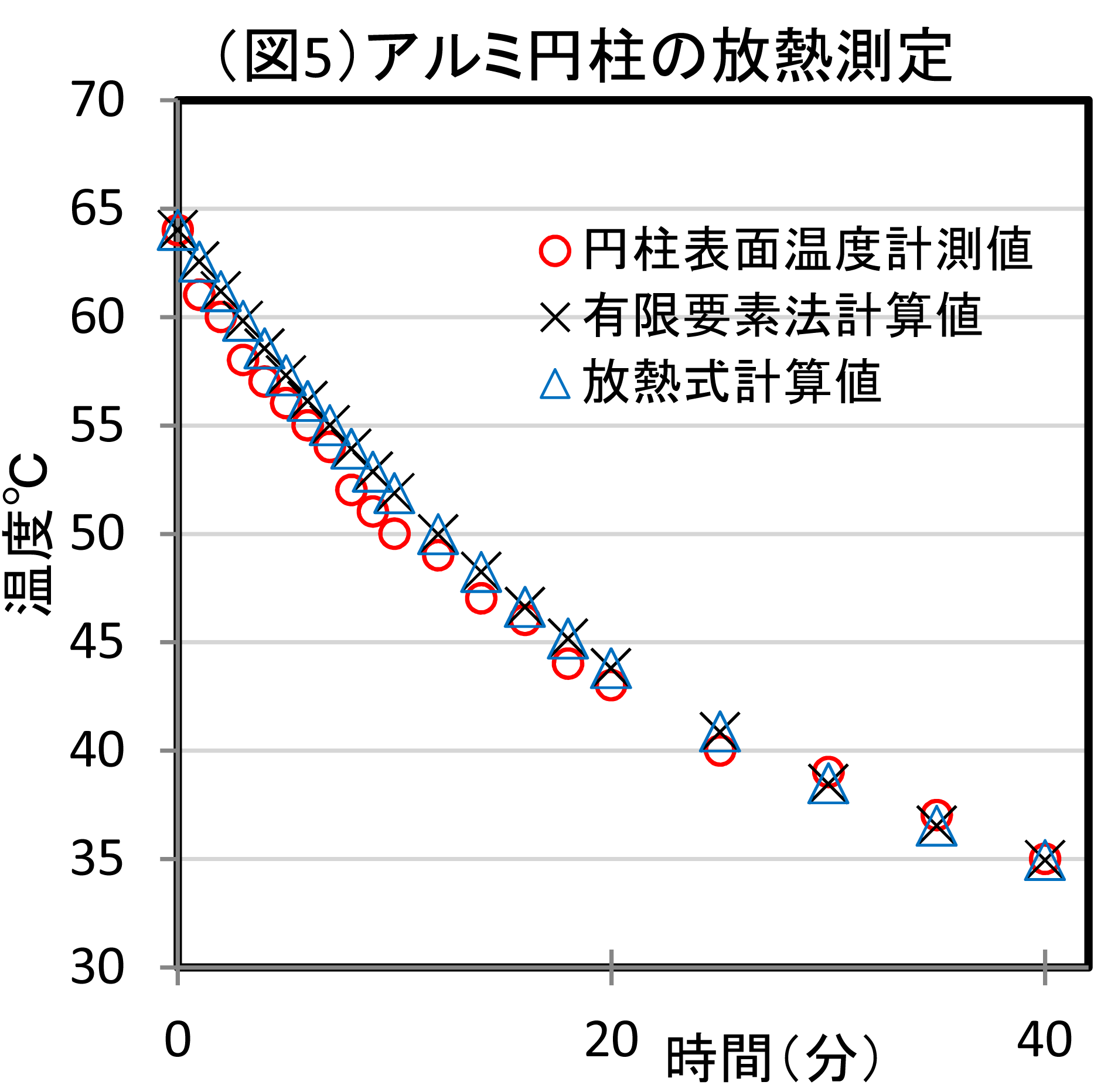
　ｔ＝ta＋(ti-ta）EXP（-K/C*τ）　　　（1）式
　　K：放熱係数＝ｈ（自然対流熱伝達率）*A（円柱表面積）として（1）式を計算した結果を（図5）に示す。
　　C：円柱の熱容量（kJ/℃）
　　ｔｉ：円柱の初期温度（64℃）、ta：室内温度（28℃）


4）自然対流熱伝達率hの算出
熱伝達係数ｈ＝λ・Nu/ℓ　　W/m＾2K
ヌッセルト数Nu＝0.625*（Pr＾２/（1.1+Pr))＾0.25*Gr＾0.25
グラスホフ数Ｇｒ＝＝ℓ＾３*g*・（θw-θ）/（ν＾２*T）
g：重力加速度ｍ/S＾2
ν：動粘性係数　ｍ＾２/ｓ
ｐｒ：プラントル数（空気）　
上記各数値は伝熱関係技術資料から入手し熱伝達率ｈを計算する。


５）温度計測結果と計算結果の考察

　・実験値と計算値の傾向がほぼ一致した。
　・放熱式計算値と有限要素法計算値はほぼ一致したものの、放熱計測後0分～20分では実測値が計算値と比較しmax1℃下回っている。逆に30分～40分ではmax0.5℃上回っている。原因としては室温の変化、表面温度を計測する温度センサーの貼り付け方などが考えられる。
しかし、自然対流による放熱が支配的な現象であることは明確に理論上で証明された。放熱式計算と有限要素法計算は共に円柱からの放熱過程をよく表しており、予測計算として十分活用できると考える。
　・ここに示した円柱実測温度は表面の温度だが、中心温度は熱伝導率が良いため表面温度に対し0.5～1.0℃であった。

（図6）円柱写真

注）計算式参照文献は、伝熱計算法（千輝淳二著、工学図書、伝熱工学の学び方（北山直方著、オーム社）