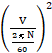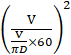|
|
|
|
|
 |
|
|
|
| 2020年5月12日改訂 |
|
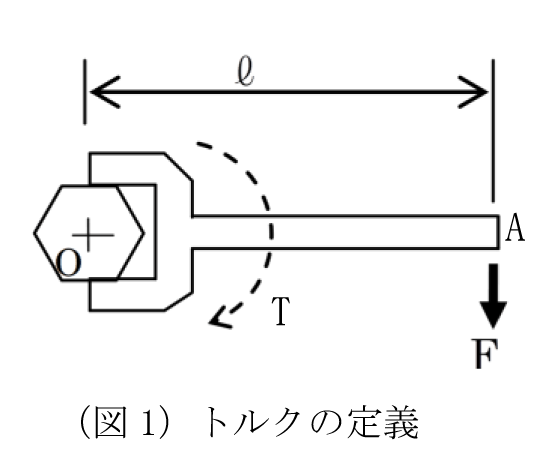
| メカトロ機械の設計にあたり、まず直面するのがどうやって動かすかである。 まずは、モーター選定に必要な知識を紹介する。 モータ動力の計算方法(摩擦負荷+慣性負荷) 2020年5月1日 遠藤 1.動力(Power)とは 動力の定義は「仕事率」である。 動力=力×速度=力× ただし、仕事=力×距離(J) 動力、すなわち仕事率の次元は“W(ワット)”
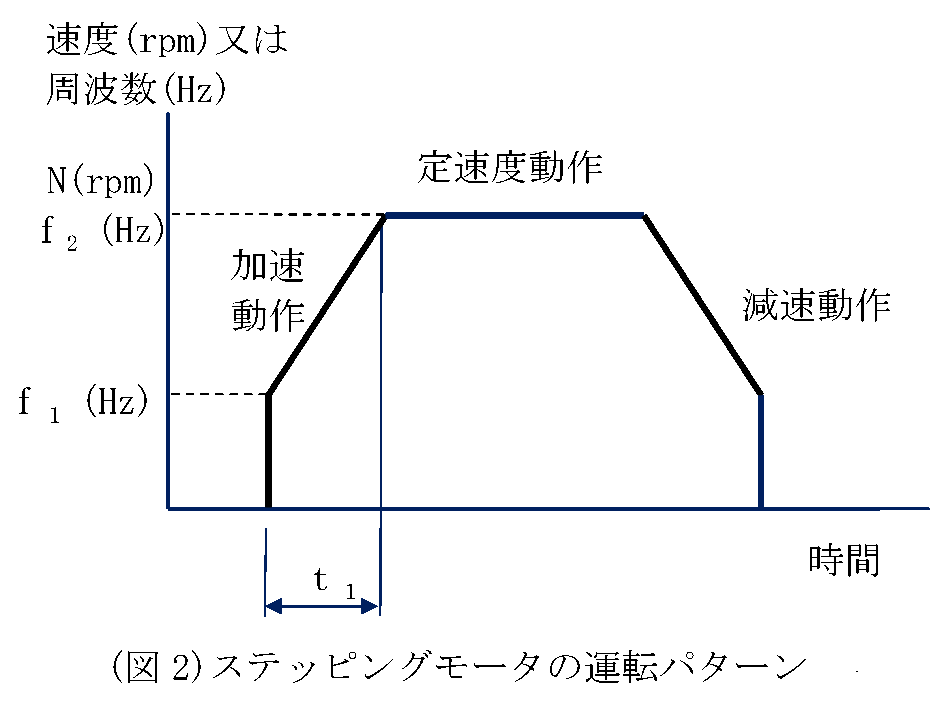
例えば、体重(質量)60kgの人が10秒間に高さ2mの階段を上った場合を考える。 この時の力は60(kg)×9.8(m/S2)=588(N) 階段を駆け上る速度はV=2(m)/10(S)=0.2(m/S) この時の動力(仕事率)はP=588(N)×0.2(m/S)=117.6(N・m/S=W) (ただし、水平方向の運動で消費される動力は無視している。) (出典:機械設計 中嶋尚正:東京大学出版会) 2.モータ動力 2.1 トルクとは (図1)にボルトをレンチで回す場合を考える。ボルトを締め付ける位置Oから距離ℓ離れたスパナの端面Aに力F(N)を加える。 この時、ボルトを回転させようとする力T(図1の点線)は T=F×ℓ (N・m) (2式) と表され、トルク(又は、モーメント)と言う。 ただし、ℓは位置Oからスパナ端面Aまでの距離(m) である。 2.2 モータ負荷トルクの種類について 1) 定速動作時の摩擦負荷トルク TF(N・m) 物体が一定速度で動作している時、物体は摩擦がなければ永久に等速運動するが、実際には速度は徐々に低下する。この理由は摩擦によるもので、物体とガイド等の摺動摩擦、又はタイヤ、車輪と軌道面との間のころがり摩擦等によって発生する摩擦力である。この摩擦力に起因するトルクを摩擦負荷トルクTFと言う。具体的な摩擦トルクの算出方法は3.1項に示す。 2) 加減速動作時の加減速負荷トルク TA(N・m) 物体が加速又は減速する時には外力を加える必要がある。この外力を発生させるために加えるトルクを加減速負荷トルクTAという。 3)モータ駆動に必要となるトルク TM(N・m)は下記のようになる。 3.1)定速度動作時 定速度動作時は摩擦負荷トルクTFだけが作用する:TM=TF 3.2)加減速動作時 加減速動作時は摩擦負荷トルクTFと加減速負荷トルクTAが同時に作用する:TM=TF+TA 3.3)ステッピングモータの台形運転パターン ステッピングモータの加減速の仕方には特徴がある。(図2)に示すように、まず、自起動周波数f1に立ち上げてから最高周波数f2まで加速を行う。この理由はステッピングモータの共振周波数が100Hz~200Hz(2相モーターの場合)の領域にあり、この周波数領域では不安定な動作となり、いわゆる脱調が起こりやすい。このため、この領域を避け、500Hz以上の周波数から加速を行うことが一般に行われている。 2.3 モータ動力P P= ただし、N:回転数(rpm) TF:摩擦トルク (N・m) 2)加減速動作に必要なモータ動力Pは(4式)となる。 P= ただし、加速トルクTAは TA=(J0+JL)× TA= ただし θS:ステッピングモータのステップ角(°) f1:自起動周波数(Hz;50Hz~1000Hz程度、100~200Hz間は避ける)(図2、3参照) f2:最高周波数(Hz)(図2参照) J0:モーターローター慣性モーメント (kg・m2) 注)kgは物体の質量 JL:負荷慣性モーメント(kg・m2) NM:サーボモーター最大回転速度(rpm) 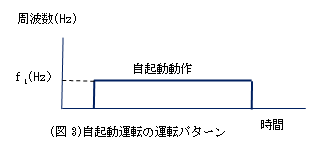 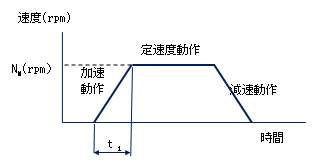 (図4)サーボモータの運転パターン 3)ステッピングモータの自起動運転時のトルクTA、最大自起動周波数f TA=(J0+JL)× ただし、n:3.6°/θS また、最大自起動周波数fは f=
本式で、慣性負荷を接続したときの最大自起動周波数を確認する。
3.駆動機構別の摩擦負荷トルクTLF [N・m] の計算式 3.1 摩擦負荷トルクの計算式 1)送りねじ駆動トルクT 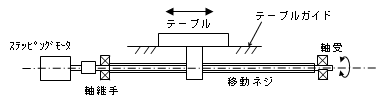
TF=
m:テーブル質量(ワーク含む)(kg) g:重力加速度 (m/s2) L:ネジのリード (m) η:ねじ効率(台形ねじ0.2~0.3、ボールねじ0.95程度) μ:テーブルガイドとの摩擦係数(約0.1) 2)ベルト駆動、ラック・ピニオン駆動トルクTF 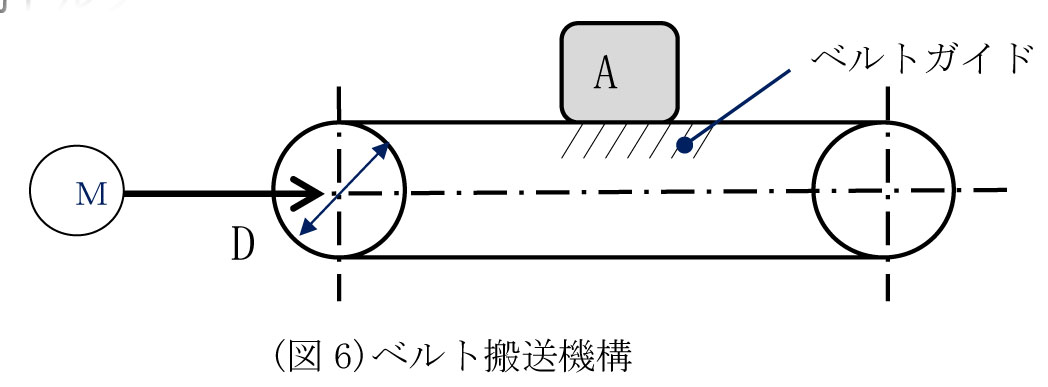
TF= m:物体Aの質量 (kg) g:重力加速度 (m/s2) D:直径プーリ(m) μ:ベルトガイドとの摩擦係数(約0.1)
3)ころがり台車トの駆動トルクTF 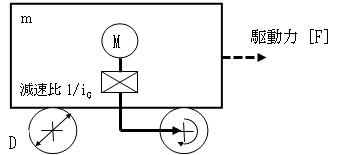
3.1)駆動力F F=
mg×μ 3.2)駆動トルクTF TF=F× m:台車質量 (kg) g:重力加速度 (m/s2) D:直径プーリ(m) 4)巻き上げトルクTF 
巻き上げトルクTF TF=mg× m:質量(kg) g:重力加速度 (m/s2) D:直径プーリ(m)
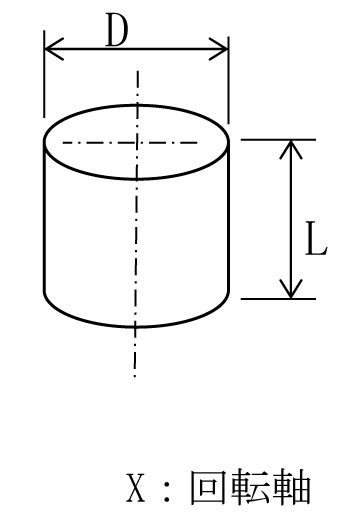
4.1 円柱の慣性モーメント(X軸回り) J= 例)D=10cm=0.1m、m=10kgの時 J=
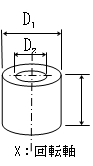
4.2 中空円柱の慣性モーメント J=
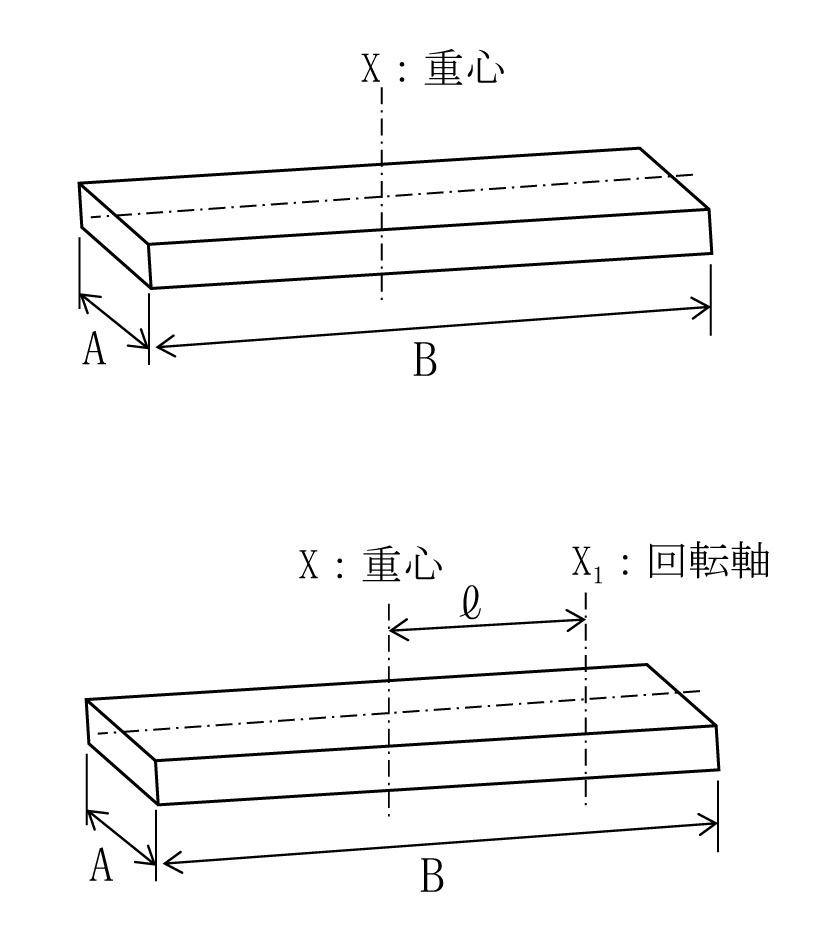
4.3 角柱の慣性モーメント J=
4.4 重心からℓ離れたX1軸に関する慣性モーメント J1= =J+mℓ2 J:x軸に関する慣性モーメント[kg·m2] J1:x1軸(重心を通る軸)に関する慣性モーメント[kg·m2] m: 質量[kg] 注)地球上では重さと考えてもよい。 D1: 外径[m] D2: 内径[m]
4.5 直線運動する物体の慣性モーメント 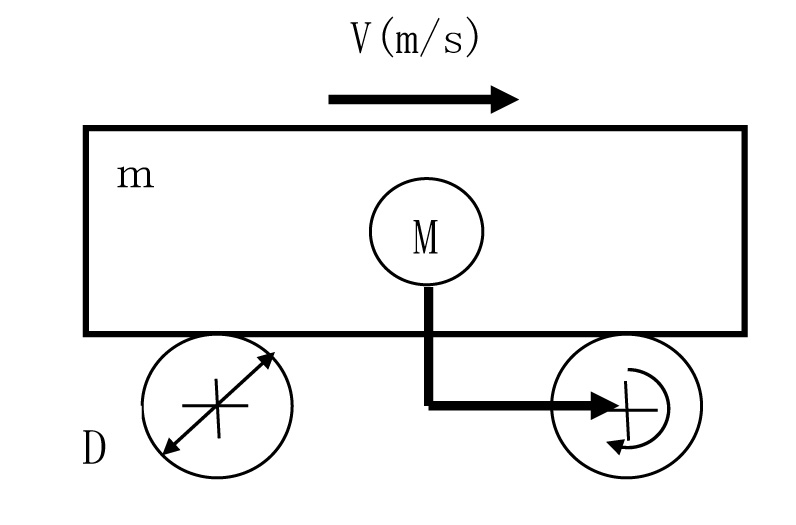
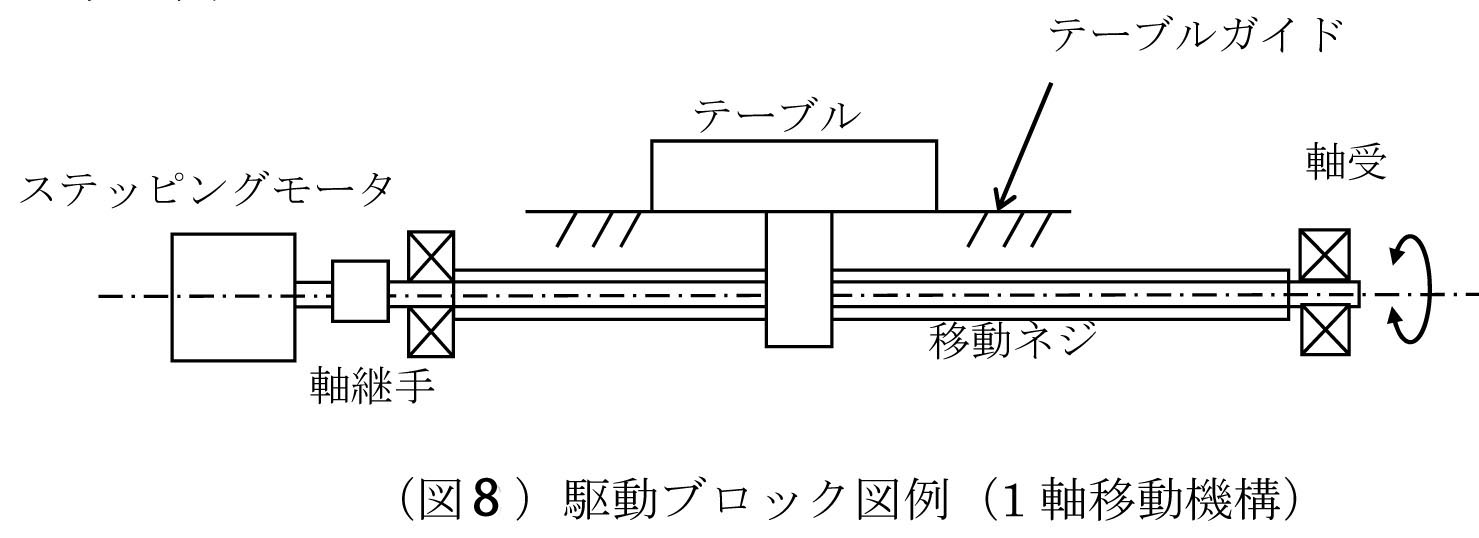
速度Vで直線運動する物体の等価慣性モーメントJは J=m× ω=2πN/60であるから J=m× N:回転数(rpm) V:移動速度(m/s) (出典:慣性モーメント設計計算P142、日刊工業) 1)ころがり台車の場合 N= J= 2)ねじ機構テーブル部 (図4)のテーブル移動速度V(m/s)、モーター回転数N(rpm)としたとき J= ただし L:ネジのリード (m) m:テーブル質量 (kg) 4.7 減速機を介した時のモータ軸換算慣性モーメントJⅿ
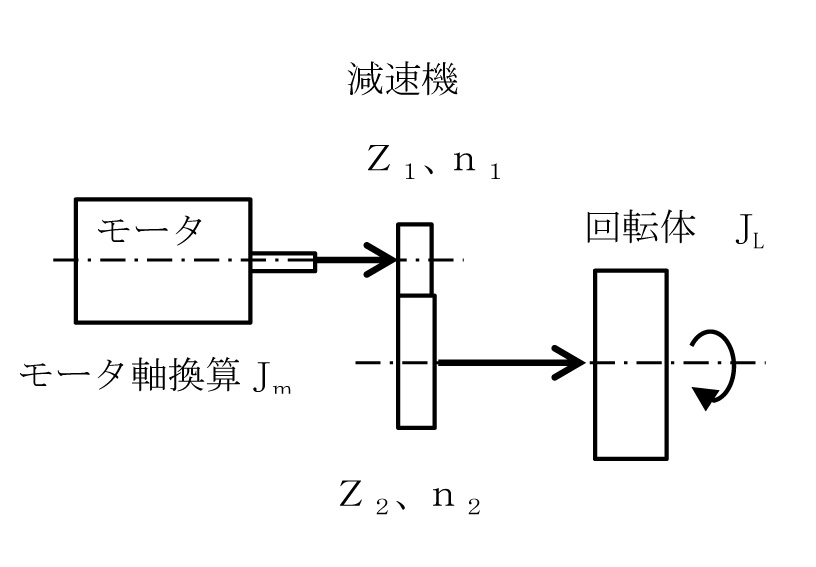
Jⅿ=
i:減速比= Z1、Z2:歯車歯数 n1、n2:回転数n すなわち、回転体の負荷慣性モーメントは減速機を入れると、そのモータ軸換算の慣性モーメントは原則比の2乗に反比例して小さくなる。
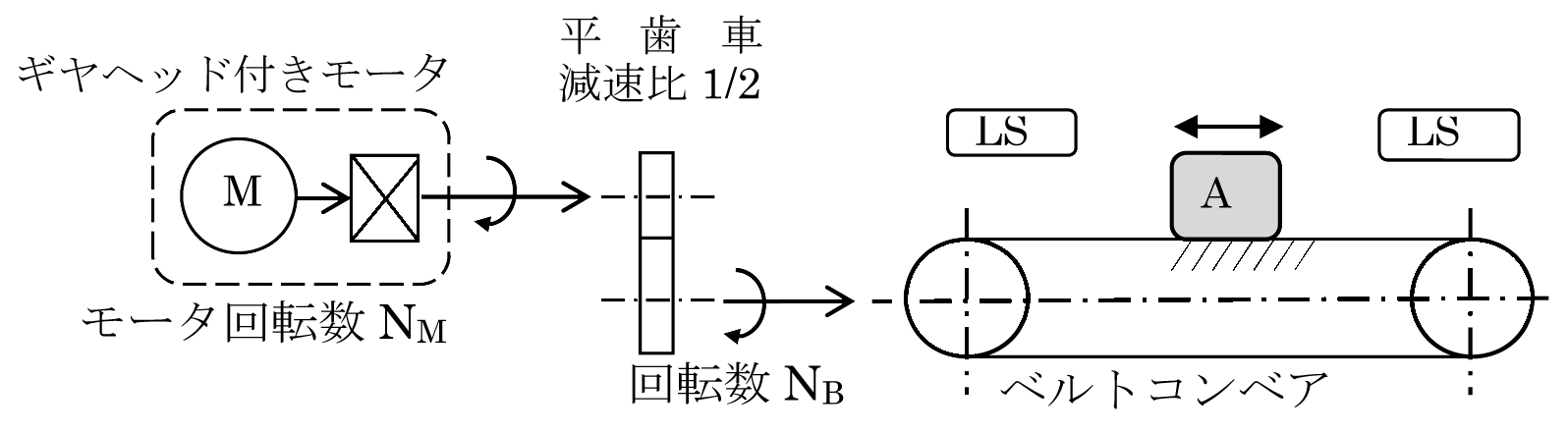
5.モータトルク(摩擦負荷)の計算 (図7)コンベア駆動ブロック図 5)モータ軸換算トルク、回転数は
2)駆動トルク、回転数 5.3 電動台車の場合 1)電車台車の仕様 ・走行速度 V=0.314m/s ・搬送重量 W=100kg ・車輪径 D=100mm ・ころがり摩擦係数 μ=0.01 ・DCモータ使用 定格回転数N(rpm)、定格トルクT(N・m) 2)ブロック図 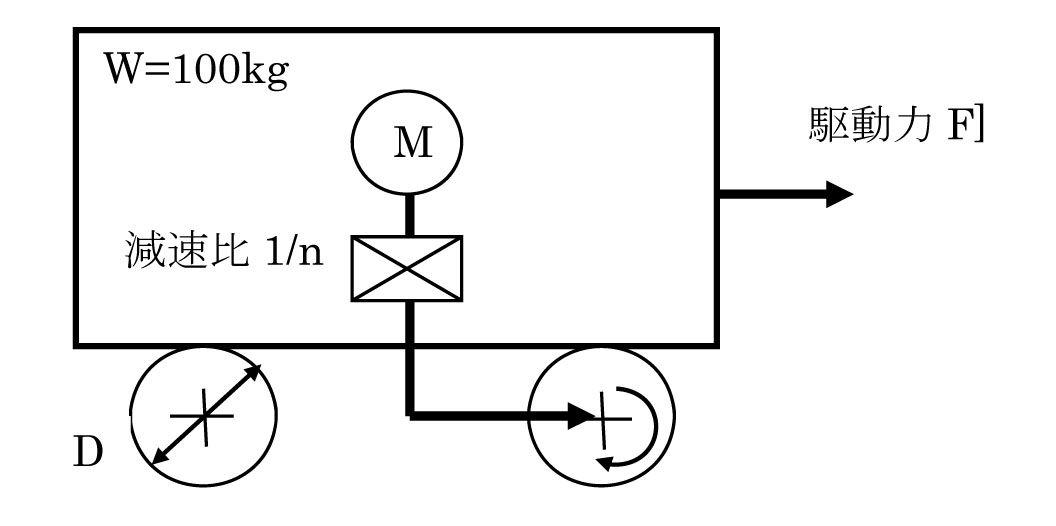 (図9)電動台車駆動ブロック図 3)駆動力F=W×μ |
|