Home page
relativistic Dirac equation
QED is wrong.
Einstein relativity is wrong
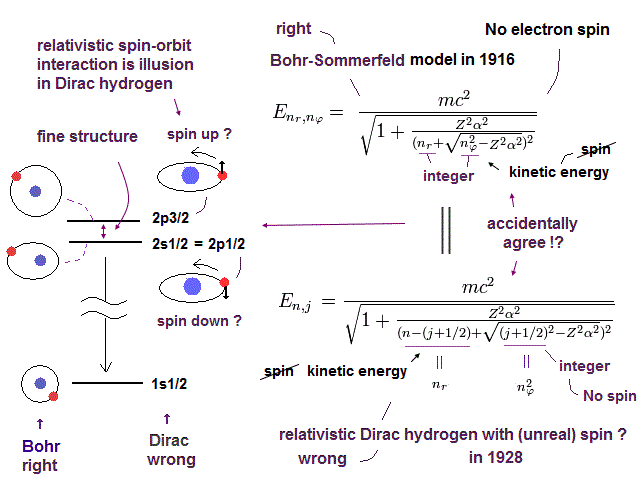
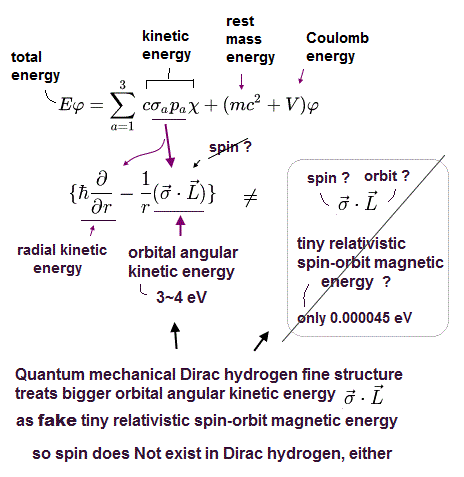
(Fig.1) Fine structure is caused Not by relativistic spin-orbit interaction of unphysical quantum mechanical Dirac hydrogen, but by real Bohr-Sommerfeld model without spin.

Experimental energy levels of a hydrogen atom and all the hydrogen-like ions agree with the (unrealistic) Schrödinger equation without spin and real Bohr-model.
The hydrogen's small energy levels' splitting (= only 0.000045eV ) between 2p3/2 and 2p1/2 called fine structure also perfectly agreed with the real Bohr-Sommerfeld model considering elliptical orbits without spin in 1916.
Later in 1928, the unphysical quantum mechanical Dirac equation managed to get the same fine structure energy solution ( this-12.4.13 ) as the real Bohr-Sommerfeld's hydrogen by relying on the paradoxical relativistic spin-orbit magnetic interaction ( this-p.2-1st,2nd-paragraphs, this-p.14, this-lower ).
Negligibly tiny Lamb shift, which cannot be observed in spectrum lines, is just thermal fluctuation or something which can Not be explained by quantum mechanics or unphysical QED that always gives meaningless infinities.
This-p.1~last~p.2 says
"The fine structure splitting 2P3/2 – 2P1/2, which according to Dirac’s
theory arises from spin-orbit interaction, agrees exactly with the separation of the two levels of Sommerfeld’s 1916 theory (= without spin )."
This-5th-paragraph says
"Between 1913–16, Sommerfeld developed Bohr's model, introducing elliptical orbits, ..., it turns out, perfectly predicts the fine structure of the hydrogen spectral lines. That is, it gives exactly the same formula as the fully relativistic Dirac quantum mechanics of 1928, and it gives better predictions for this phenomenon than basic (1925) Schrödinger–Heisenberg quantum mechanics. Since the success (of Bohr-Sommerfeld model ) is so dramatic,"
This-p.8-5th-paragraph says
"an
exact solution of Dirac’s equation gave an expression for the discrete energy levels of
the hydrogen spectrum which was identical to Sommerfeld’s original formula derived in
1915, which was in good agreement with experimental results"
The electron spin is unreal, wrong, needing the paradoxically faster-than-light spinning, which can be naturally replaced by the real orbital motion with the same magnetic moment called Bohr magneton ( this-p.2 ).
The unphysical quantum mechanics claims the 2p3/2 state has the total angular momentum j = 3/2, which is the sum of the orbital angular momentum l = 1 and the up-spin angular momentum s = 1/2.
And the 2p1/2 state is supposed to have the total angular momentum j = 1/2, which is equal to the orbital angular momentum l = 1 minus (down-)spin 1/2 ( this-p.1-p.2 ).
As shown in Fig.1-lower, this total angular momentum number j allegedly including the (unphysical) spin s ( this-last ) just agrees with the orbital angular momentum number (= nφ ) of the real Bohr-Sommerfeld hydrogen without spin.
nr is radial kinetic energy number ( this-p.12, this-p.10 ).
The radial nr = principal total energy quantum number n - angular kinetic energy j.
See the real Bohr-Sommerfeld's fine structure energy ( this-p.10-upper ), which was copied by the Dirac hydrogen energy later.
↑ This accidental agreement is unnatural, meaning the fine structure is due to the real Bohr-Sommerfeld model without spin, which was illegitimately copied by the unphysical quantum mechanical Dirac hydrogen with the paradoxical spin later.
Actually, even this quantum mechanical Dirac hydrogen's fine structure is Not caused by the relativistic spin-orbit interaction but by the orbital motion (= without spin ), which is why Dirac's fine structure agreed with Bohr-Sommerfeld model without spin.
This real Bohr-Sommerfeld model without spin-orbit interaction does Not use the paradoxical Einstein relativity
(Fig.2) Relativistic spin-orbit magnetic interaction disappears or appears seen from the rest frame of a nucleus or a moving electron, which is paradox, so wrong
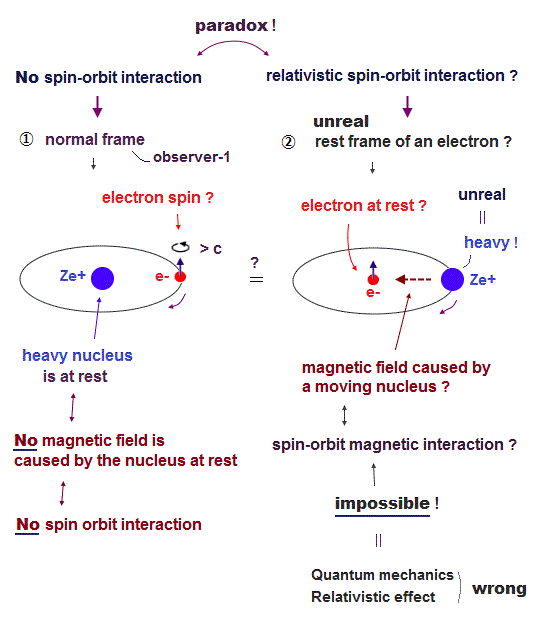
The present unphysical mainstream quantum mechanics heavily relies on the paradoxical relativity in the (relativistic) spin-orbit interaction or spin-orbit coupling = fine structure tiny energy splitting of a hydrogen atom.
This relativistic spin-orbit interaction is self-contradictory, impossible, and it can disprove Einstein relativistic theory, too.
When an electron is moving around a heavy nucleus at rest (= in the lab or rest frame of a nucleus ), the nucleus at rest cannot produce magnetic field (= No charge motion in the stationary nucleus = No electric current I = No magnetic field B ), hence, the electron can only feel electric field and cannot feel magnetic field from the stationary nucleus ( this-① ).
↑ No relativistic spin-orbit magnetic effect as seen by a nucleus means quantum mechanical fine structure based on this paradoxical relativistic spin-orbit magnetic interaction is wrong.
Einstein relativistic theory does Not have the absolute frame, all things must be relative, which causes fatal twin and length paradoxes.
So in the crazy Einstein relativistic world, we have to think about the electron's rest frame where the originally-stationary heavy nucleus appears to be moving around the stationary electron that is originally moving ( moving electron ↔ moving nucleus ).
↑ In this unphysical electron's rest frame, the fictitiously-stationary electron with spin can feel (fake) magnetic field from the nucleus that appears to be moving around the electron, though it is impossible for a heavier nucleus to be moving around a lighter electron due to violation of momentum conservation (= so Einstein relativity is false ).
This fake magnetic field caused by the unrealistically-rotating nucleus is said to cause the (fictitious) spin-orbit magnetic interaction in the position of the (fake) stationary electron with spin, depending on the electron spin's up (= magnetic energy higher ) or down (= magnetic energy lower ) directions ( this p.3-4 ).
Quantum mechanics or mainstream relativistic quantum field theory called Dirac equation claims this (fake) spin-orbit magnetic interaction is the origin of fine structure tiny energy splitting between 2p1/2 (= down-spin + orbital angular momentum = 1 ) and 2p/3/2 (= up-spin + orbital angular momentum = 1 ) of the hydrogen atom.
But as you notice, this relativistic spin-orbit (fake) magnetic interaction is physically impossible and paradoxical.
Because this fake relativistic spin-orbit magnetic interaction or fine structure energy splitting is said to be generated only in the (unphysical) electron's rest frame (= seen by the moving electron ).
And in the normal lab nuclear rest frame seen by a stationary nucleus (= generating No magnetic field ), this spin-orbit interaction or fine structure energy splitting does Not occur, according to their logic ( this p.10 ).
This p.3-Fig.3 (or this p.3-Figure 3 ) says
"Although in the rest frame of the nucleus, there is No magnetic field
acting on the electron (= No spin-orbit interaction ), there is a magnetic field in the rest frame of the
electron (= spin-orbit interaction )" ← paradox !
↑ Different frames seen from different observers (= depending on seen from stationary nucleus or stationary electron ) cause spin-orbit magnetic interaction or No spin-orbit interaction, which is clearly paradox, wrong, and disproving Einstein relativistic theory and quantum mechanical fine structure theory.
An observer seeing from the stationary nucleus cannot observe the spin-orbit fine structure energy splitting, while only an observer seeing from the moving electron can paradoxically see the spin-orbit fine structure splitting.
And it is physically impossible for a heavier nucleus to be unrealistically moving around a lighter (stationary) electron due to momentum conservation and action-reaction law (= when two objects attract each other, the lighter object or electron must be moving faster than the heavier one or nucleus to conserve total momentum ).
This paradoxical relativistic spin-orbit fine structure energy splitting is said to be explained by relativistic Dirac equation for hydrogen, but this is wrong.
Because the Dirac equation for hydrogen deals only with the nuclear rest frame (= with only static Coulomb electric potential V ) with moving electron (= contrary to the standard explanation of the spin-orbit effect, Dirac hydrogen cannot deal with the electron's rest frame seen by the moving electron or fictitious magnetic field potential from the unrealistically-moving nucleus).
Actually, Bohr-Sommerfeld model without spin could perfectly explain the hydrogen's fine structure energy splitting, and later, Dirac hydrogen copied it and obtained exactly the same fine-structure energy values as the older Bohr-Sommerfeld model ( this-lower, this p.14 ). ← Dirac equation with spin = Bohr-Sommerfeld model without spin !
In fact, the relativistic Dirac equation's fine structure energy splitting value is just a part of electron's orbital kinetic energy (= Dirac equation's γ or σ matrix allegedly representing spin comes from electron's kinetic energy, this p.30, this-2.(1)-(5) ), which has nothing to do with the relativistic spin-orbit magnetic interaction (= Dirac equation changing spin j from down to up or increasing j by one corresponds to Bohr-Sommerfeld's angular kinetic energy nφ increasing by one ).
In condensed matter physics like spin-Hall-effect, physicists artificially changed the original Einstein's tiny relativistic spin-orbit interaction constant by using fake electron's effective mass, which is unreal, inconsistent with the original Einstein relativistic theory ( this p.5, this p.5-6, this-p.24-pseudo-spin ).
Quantum mechanics has to rely on artificially-created fictional pseudo-potentials (= which is Not prediction of quantum mechanics nor Einstein relativity ) to (wrongly) explain the (fake) spin-orbit interaction in today's mainstream density functional theory (= fake ab-initio DFT that cannot predict anything ).
As a result, the relativistic spin-orbit interaction is paradoxical and non-existent.
(Fig.3) The change of spin j value in Dirac hydrogen affects the non-spin Schrödinger's hydrogen energy part, which shows quantum mechanical Dirac's spin-orbit interaction is just orbital kinetic energy like Bohr-Sommerfeld model, Not spin.
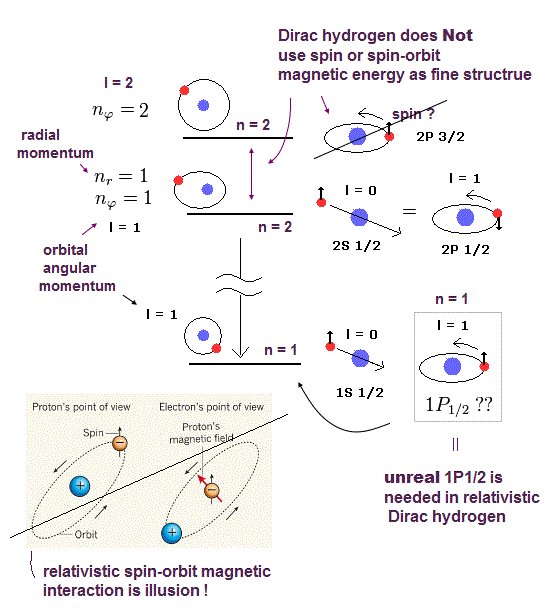
(Fig.4) Dirac hydrogen spin j is Not spin but orbital angular momentum kinetic energy of Schrodinger's hydrogen (= or Bohr Sommerfeld model ) ↓
Quantum mechanical Dirac equation's hydrogen fine structure energy allegedly contains the tiny (paradoxical) relativistic spin-orbit magnetic energy splitting expressed using the total angular momentum number j = spin s + orbital l ( this-p.18, this-p.9-p.10 ).
But this relativistic Dirac's hydrogen energy is approximately equal to the non-relativistic Schrödinger's hydrogen's (or Bohr model's ) energy E without spin ( this-p.28, this-p.6 ) which non-spin Schrödinger's hydrogen's energy also paradoxically includes this Dirac's spin quantum number j ( this-p.21-(6.32)(6.34), this-p.7-(32), this-p.29-middle,p.33 ).
See this-p.30-(2.78),p.31-(2.89),p.40-(2.140), this-p.40(or p.34)-lower~p.41-2nd-last-paragraph
↑ When the (fictional ) spin changes from down (= j = 1/2 ) to up (= j = 3/2 ) in tiny fine structure, the relativistic Dirac hydrogen's total energy, which is approximately equal to non-relativistic Schrodinger's hydrogen without spin, increases orders of magnitude more (> 2eV ) than the tiny fine structure energy (= just 0.000045 eV ).
↑ It means the quantum mechanical Dirac's hydrogen's fine structure related to the total spin quantum number j is Not caused by the relativistic spin-orbit interaction but by the orbital angular momentum (= orbital angular kinetic energy far larger than the tiny spin-orbit energy ) affecting the non-relativistic, non-spin Schrodinger's hydrogen energy or real Bohr-Sommerfeld model without spin.
If quantum mechanical fine structure is due to relativistic spin-orbit magnetic energy, its Dirac hydrogen energy must contain 3 variables of radial, orbital and spin.
But actually, the quantum mechanical Dirac hydrogen's energy contains of only 2 variables of radial (= nr ) and orbit (= j = Not spin ! ), or 2 variables of principal quantum number n and angular momentum j.
↑ This means quantum mechanical Dirac hydrogen's fine structure has nothing to do with spin-orbit interaction.
↑ Non-spin Schrödinger's hydrogen's energy contains only 2 variables of nr (= radial ) and l (= orbital angular momentum. n = nr + l, this-3rd-paragraph, "m" is just the direction of orbital angular momentum l, this-(4.10.7)-(4.10.8), this-p.35 ). ← Dirac's hydrogen must contain at least 3 variables by adding spin number, if it really expresses spin-orbit interaction (= actually, Dirac hydrogen contains only 2 variables of n and j without spin ).
↑ When the total angular momentum j is changed, Dirac hydrogen cannot distinguish the case of only spin changed from the case of orbital angular momentum (= l ) changed (= because Dirac hydrogen also doesn't use spin, and "j" means orbital angular momentum ).
(Fig.6) Quantum mechanical Dirac's hydrogen 2p1/2 state with (fictional) down spin is equal to real Bohr-Sommerfeld model's orbit without spin.

Quantum mechanical Dirac hydrogen's 2p1/2 energy (= j = 1/2, nr = 1, n = 2 ) in fine structure is "accidentally" equal to the real Bohr-Sommerfeld's hydrogen energy of an elliptical orbit without spin (= radial nr = 1, orbital angular nφ = L = 1 ).
This unnatural accidental coincidence shows the fine structure energy splitting is due to the real Bohr-Sommerfeld's orbital motion, which was wrongly copied by the quantum mechanical Dirac equation with the unphysical spin-orbit interaction later.
(Fig.7) The unphysical Dirac's hydrogen 2p3/2 can be replaced by the real Bohr-Sommerfeld fine structure energy level without spin.
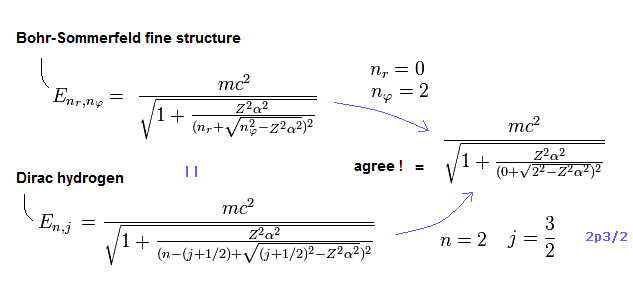
As shown in Fig.7, the quantum mechanical Dirac's hydrogen's 2p3/2 with unphysical up-spin (= j = 3/2, nr = 0, this-p.29 ) has exactly the same energy as the real Bohr-Sommerfeld model (= nr = 0, orbital nφ = 2 ).
↑ It shows the quantum mechanical Dirac hydrogen's total spin angular momentum number j + 1/2 is equal to the orbital angular momentum number nφ of Bohr-Sommerfeld hydrogen without spin.
The hydrogen's tiny fine structure energy splitting between 2p1/2 and 2p3/2 is said to be caused by the relativistic spin-orbit magnetic interaction induced by flipping spin from down (= 2p1/2 ) to up (= 2p3/2 ), which is wrong.
↑ Just changing this spin j from down-spin of 1/2 (= 2p1/2 ) to up-spin of 3/2 (= 2p3/2 ) drastically increases the Dirac hydrogen energy (= approximately equal to Schrodinger hydrogen's energy ) as much as the orbital kinetic energy (> 2eV ) far larger than the tiny relativistic spin-orbit magnetic energy (= 0.000045 eV ).
Dirac hydrogen's 2p3/2 must decrease the radial kinetic energy (= nr = 0 ) from the 2p1/2 (= nr = 1 ) to get the tiny fine structure energy difference by canceling the large orbital kinetic energy change induced by changing j = 1/2 → j = 3/2 (= keeping the same principal quantum number n = 2 ).
(Fig.8) Dirac hydrogen is unreal, relying on many unnatural coincidences.

The quantum mechanical or relativistic Dirac hydrogen energy E depends only on the total angular quantum number j (= spin + orbital angular momentum ) and radial kinetic energy (= nr, or total energy number n = nr + j + 1/2 ).
↑ This means the Dirac hydrogen is unreal, relying on many unnatural coincidences between different energy levels such as 2p1/2 = 2p1/2 (= both of which have the same j = 1/2, n = 2, but have different orbital angular momentums ), 3s1/2 = 3p1/2 (= both have j = 1/2, n = 3 )... this-p.20, this-p.6-table.1, this-p.45
↑ These many unnatural coincidences among completely different energy states are unrealistic, impossible, showing the hydrogen's fine structure is due to the real Bohr-Sommerfeld model without spin.
It is said that there is negligibly tiny energy splitting called Lamb shift between 2s1/2 and 2p1/2 (= disagreeing with Dirac hydrogen ), which can Not been explained by today's quantum mechanics nor even quantum electrodynamics (= QED ) that just artificially manipulates free parameters and illegitimately removes infinites by ad-hoc renormalization ( this-p.3-left-3.2 ).
This tiny Lamb shift is just small thermal fluctuation, other smaller fine structure energy splitting or artifact caused by external magnetic field, irrelevant to the (unreal) QED virtual particles or the (unseen ) 2s1/2-2p1/2 energy difference.
(Fig.9) Unphysical Dirac hydrogen always requires different orbital l in the same j, which causes many unreal energy states, disproving Dirac fine structure.

The quantum mechanical Dirac hydrogen always needs two different orbital angular momentum states (= l = j ± 1/2 ) in each total angular momentum j ( this-p.18-top-(6.7) ).
It means obtaining the hydrogen's ground state energy (= 2s1/2 with zero orbital angular momentum ) also needs the unreal 1p1/2 state (= with non-zero orbital angular momentum in the ground state ) that does Not exist in quantum mechanical hydrogen ( this-p.6, this-p.2 ).
↑ So the Dirac hydrogen's 1s ground state's wavefunction paradoxically contains the unreal 1p1/2 orbital angular kinetic energy variables such as θ and φ which are Not included in the original hydrogen's 1s state ( this-p.41-upper, this-p.3-upper, this-p.70 ).
In the same way, obtaining 2p3/2 (= orbital angular momentum l = 1 = j - 1/2 ) also needs the unreal 2D3/2 (= orbital angular momentum l = 2 = j + 1/2 ).
As a result the quantum mechanical Dirac hydrogen's fine structure is unreal, based on fictional energy states, which must be replaced by the real Bohr-Sommerfeld model without spin.
(Eq.1) Einstein relativistic energy equation without spin splits into unphysical Dirac equation whose 4 × 4 γ matrices are wrongly treated as electron spin.

(Eq.1') Unphysical 4×4 γ matrices consisting of 2×2 Pauli σ matrices treated as fake spin
Einstein paradoxical relativistic energy (= E ), momentum (= p ), mass (= m ) quadratic equation is split into the Dirac equation with unphysical 4 × 4 γ matrices.
These γ matrices consist of 2 × 2 Pauli σ matrices that are wrongly treated as the (unphysical) electron spin ( this-p.8-3rd-paragraph ).
↑ As shown in Eq.1, these Pauli σ matrices are just part of momentum p ( this-p.5, this-2.(1)(2) ) or kinetic energy ( this-p.30 ) irrelevant to the tiny relativistic spin-orbit magnetic energy of the fine structure.
(Eq.2) Pauli σ matrix (= part of momentum p ) is wrongly treated as (fictional) electron spin in Dirac hydrogen.
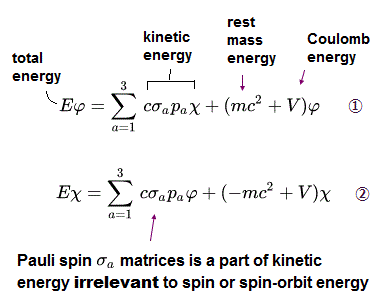
From Eq.1, we get the above Eq.2.
As shown in Eq.2, Pauli σ matrices in Dirac equation is just part of kinetic energy or momentum p irrelevant to the electron spin.
So contrary to the standard explanation, Dirac hydrogen's spin-orbit (= σL ) interaction is Not spin but just part of orbital kinetic energy.
(Eq.3) Artificial math trick using Pauli σ matrices.

Using Pauli σ matrix unphysical math trick, we can get Eq.3 ( this-p.17 ).
(Eq.4) Dirac hydrogen's spin (= σ ? )-orbit L interaction is just angular orbital kinetic energy irrelevant to relativistic spin-orbit magnetic energy.

Using the math tick of Eq.3, the Dirac hydrogen's kinetic energy part (= σp ) can be split into the radial kinetic energy (= derivative with r ) and orbital angular kinetic energy (= σL, this-p.3(or p.2) ).
As shown in Eq.4-lower, the σL is just orbital angular kinetic energy ( this-p.14, this-p.33-34-(2.104) ), but wrongly interpreted as (illusory) relativistic spin-orbit magnetic interaction by Dirac hydrogen ( this-p.4,p.7 ).
The kinetic energy (= total energy minus Coulomb potential energy ) consists of the radial and orbital angular kinetic energies ( this-p.10, this-p.6 ).
↑ If this σL means the tiny spin-orbit magnetic energy, this Dirac hydrogen (= radial kinetic energy + tiny spin-orbit σL magnetic energy ? ) unrealistically does Not contain the orbital angular kinetic energy.
(Eq.5) Total angular momentum J = orbital L + (fake) spin 1/2σ
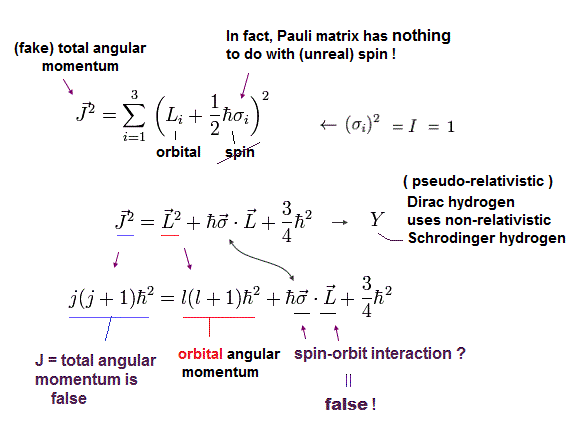
Unphysical Dirac hydrogen tries to (mis)interpret the Pauli σ matrices (= just part of kinetic energy ) as (illusory) relativistic spin-orbit magnetic interaction.
In Eq.5, the total angular momentum J (= j ) is the sum of orbital (= L ) and (fake) spin expressed as 1/2σ
The square of the total angular momentum J2 = j(j+1) and orbital angular momentum L2 = l(l+1).
And they (falsely) claim Pauli σL is the relativistic spin-orbit interaction.
(Eq.6) in case of 2p1/2 = orbital angular momentum l = 1 = j (= 1/2 ) + 1/2
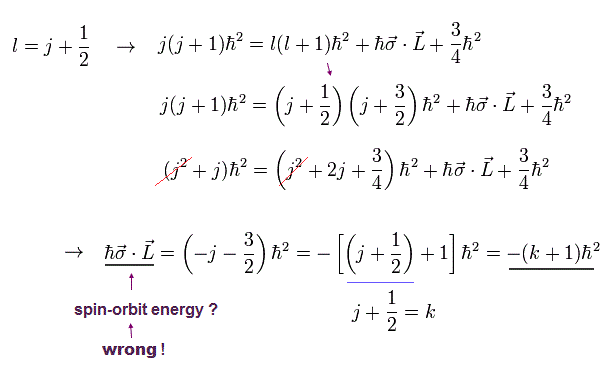
Eq.6 shows the case of 2p1/2 whose total angular momentum j = 1/2 and orbital angular momentum l = 1 (← l = j + 1/2 ), which l = j + 1/2 relation is inserted into Eq.5 to get (fake) spin-orbit interaction (= σL ) equal to -(j+1/2 + 1) = -(k +1) where k = j + 1/2.
(Eq.7) In 2p3/2, orbital angular momentum l = 1 equal to total angular momentum j = 3/2 minus 1/2
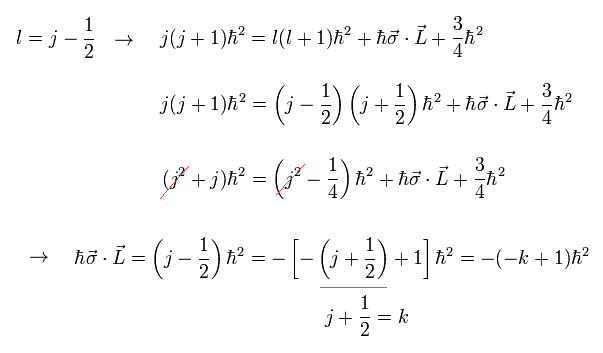
In 2p3/2, the orbital angular momentum l = 1 is equal to total angular momentum j = 3/2 minus 1/2.
This relation of l = j - 1/2 into Eq.5, we obtain the (fake) spin-orbit (= σL ) interaction as (j - 1/2) = -(-k+1) where k = j + 1/2
(Eq.8) σp → σL is just kinetic energy irrelevant to relativistic spin-orbit magnetic energy in unphysical Dirac hydrogen.
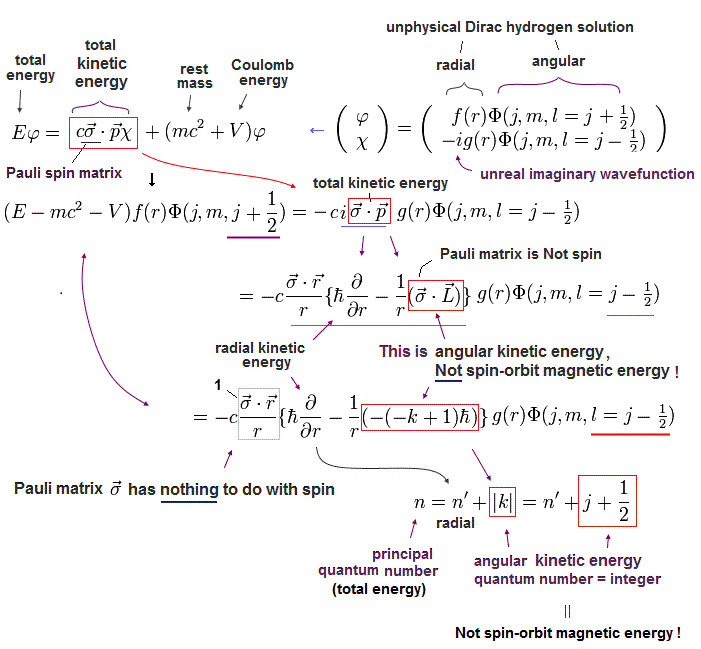
Using Eq.4, the kinetic energy part (= σp ) of the Dirac's upper equation of Eq.2 is divided into radial kinetic energy (= derivative with r ) and the orbital angular kinetic energy (= σL ).
In the upper Eq.8, this orbital kinetic energy operator σL acting on the unphysical Dirac wavefunction Φ( l = j-1/2 = 2p3/2 case ? ) is changed into -(-k+1) where k = j + 1/2 ( this-p.22-(101) ).
↑ This Dirac hydrogen wavefunction consists of the ordinary Schrodinger hydrogen's spherical Harmonics Φ (or Y ) without spin.
So this σL operator changed into total angular momentum j (= spin + orbit ? ) has nothing to with spin, contrary to Dirac's interpretation.
(Eq.9) Dirac hydrogen: kinetic energy (= σp ) is split into orbital angular kinetic energy (= σL ) that is falsely treated as relativistic spin-orbit magnetic interaction.
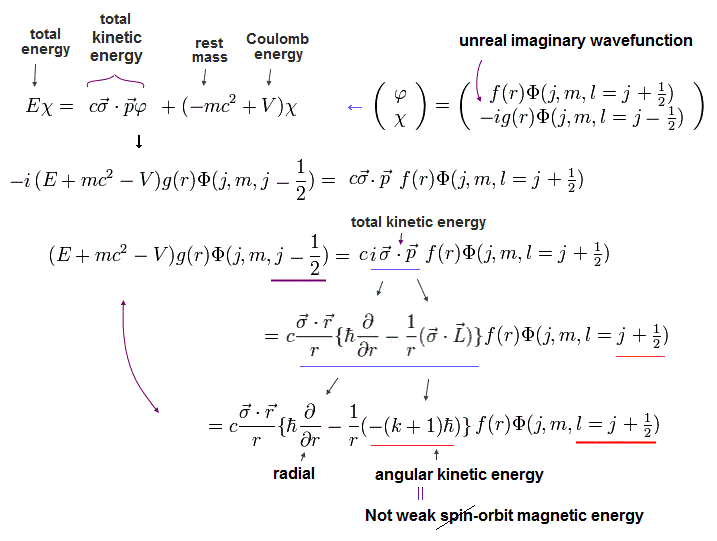
Using Eq.4, the kinetic energy part (= σp ) of the 2nd Dirac equation of Eq.2 is split into the radial kinetic energy and orbital angular kinetic energy (= σL ) which is falsely treated as (fake) spin-orbit interaction in Dirac hydrogen.
In the upper Eq.9, this fake spin-orbit σL operator acting on Schrodinger hydrogen's spherical Harmonics Φ( l = j + 1/2 = 2p1/2 case ? ) is changed into -(k+1) where k = j + 1/2.
↑ The point is these Pauli σ matrices, which are just part of kinetic energy in Dirac equation, are wrongly treated as (imaginary) electron spin, as shown in the change of j (in σL operator ) drastically increasing Dirac's hydrogen total energy far more than tiny relativistic spin-orbit magnetic energy.
(Eq.10) Artificial math trick of Pauli σ matrices acting on Schrodinger hydrogen wavefunction Y without spin.

Relativistic Dirac's hydrogen's (angular) wavefunction consists only of ordinary non-relativistic Schrodinger's hydrogen spherical Harmonics Y ( this-p.4-2.1, this-p.44-(4.48) ) without spin (= m±1/2 and j±1/2 of Y become integers, this-p.29,p.31 ).
The upper Eq.10 shows one of math tricks of changing the artificially-defined Dirac's hydrogen wavefunctions Φ of l = j + 1/2 ↔ l = j - 1/2 forms.
As shown here, Pauli σ matrices are related to Schrodinger's hydrogen's spherical Harmonics Y in Φ without spin, so σL has nothing to do with spin-orbit interaction.
(Eq.11) ↓ Dirac hydrogen's spin j just means orbital kinetic energy without spin.
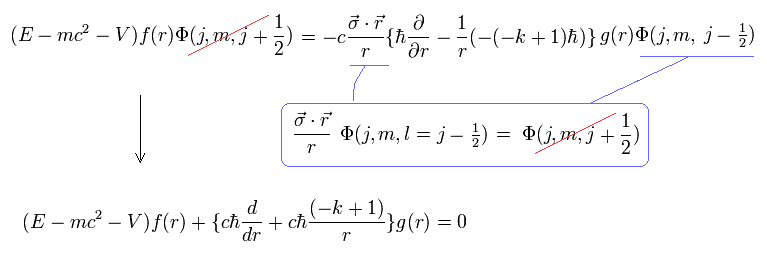
From Eq.8 and Eq.10, we obtain the upper Eq.11 where the alleged spin of the total angular momentum j is just orbital kinetic energy irrelevant to spin.
(Eq.12) Dirac hydrogen consists of radial and orbital kinetic energies, Coulomb potential energy V with No relativistic spin-orbit magnetic interaction

From Eq.9 and the artificial math trick of Eq.10, we obtain the upper Eq.12 where the alleged spin included in j is just part of orbital kinetic energy irrelevant to spin.
See this-p.17-p.20
We replace the radial functions of f(r) and g(r) by
(Eq.13)
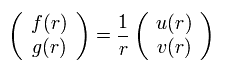
Substituting Eq.13 into Eq.11, we have the following Eq.14 ( this p.2, this p.19, this p.22~, this p.21~ )
(Eq.14) Dirac hydrogen uses Coulomb potential energy V in the rest frame of a nucleus irrelevant to relativistic spin-orbit magnetic energy seen by the moving electron.
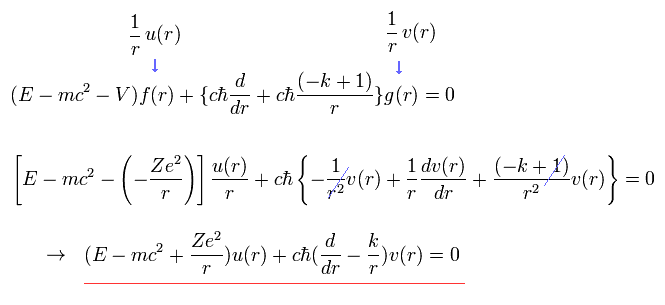
Coulomb potential V in the rest frame of a nucleus is used in Dirac hydrogen that does Not express the relativistic spin-orbit magnetic interaction in the rest frame of a moving electron
In the same way, substituting Eq.13 into Eq.12, we have
(Eq.15)
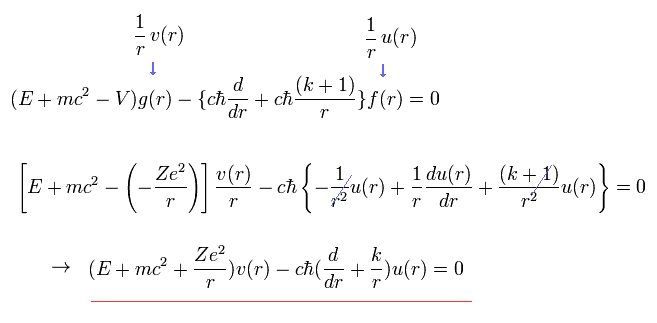
We expand u(r) and v(r) as follows,
(Eq.16)
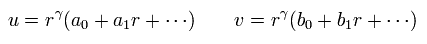
Substituting Eq.16 into Eq.14 and Eq.15, and seeing the power of γ-1, we have
(Eq.17)
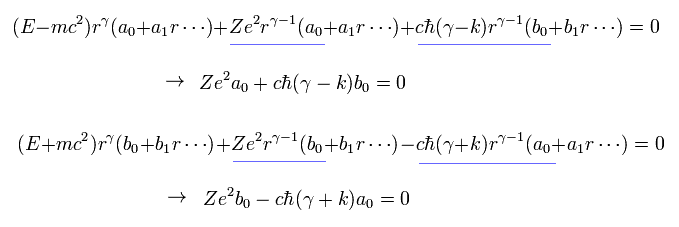
To avoid the solution of a0= b0 = 0 in Eq.17, the following relation must be satisfied.
(Eq.18)
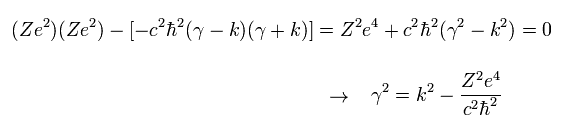
To avoid the divergence at the origin, the γ must be plus as follows,
(Eq.19)

To converge at r → ∞, we suppose u(r) and v(r) satisfy
(Eq.20)

And at r → ∞, Eq.14 and Eq.15 become
(Eq.21)

Substituting Eq.20 into Eq.21, we have
(Eq.22)
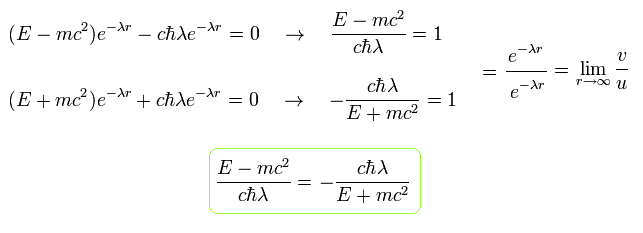
From Eq.22, λ (= plus) becomes
(Eq.23)
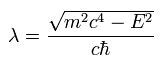
Considering Eq.16 and Eq.20, we can express u(r) and v(r) as follows,
(Eq.24)
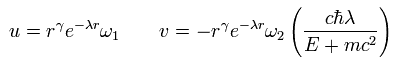
As you may notice, the replacement of Eq.24 is very similar to Schrodinger's hydrogen.
So also in Dirac's hydrogen, unrealistically, radial wavefunctions are always from zero to infinity.
If we add 4πε (see Eq.14) to γ of Eq.19, it can be expressed by the fine structure constant (=α)
(Eq.25)
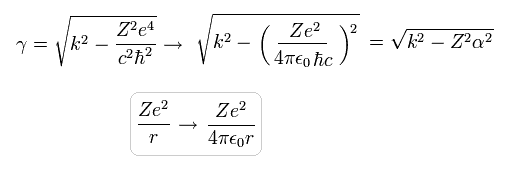
where this fine structure constant α is approximately
(Eq.26)
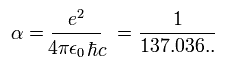
Substituting Eq.24 into Eq.14, we can get the following relations ( using Eq.23 and the green part of Eq.22 ).
(Eq.27)
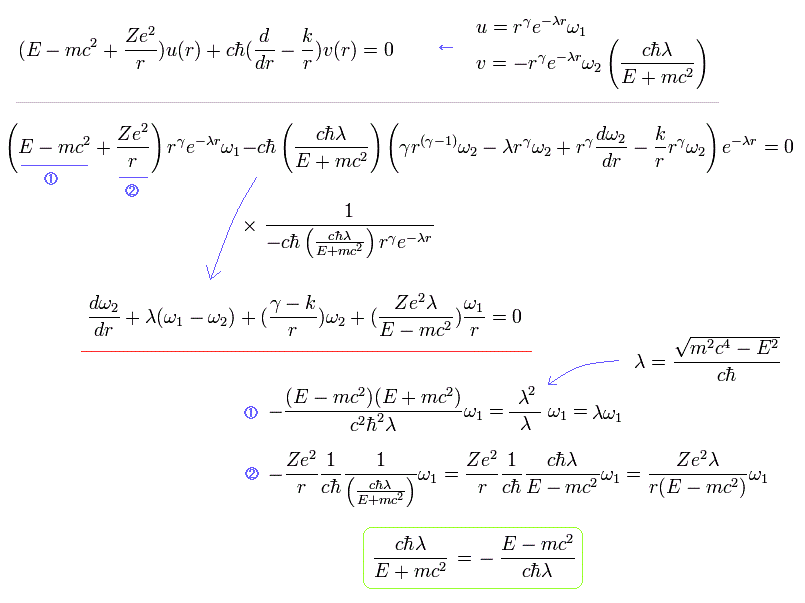
and Substituting Eq.24 into Eq.15, we have
(Eq.28)
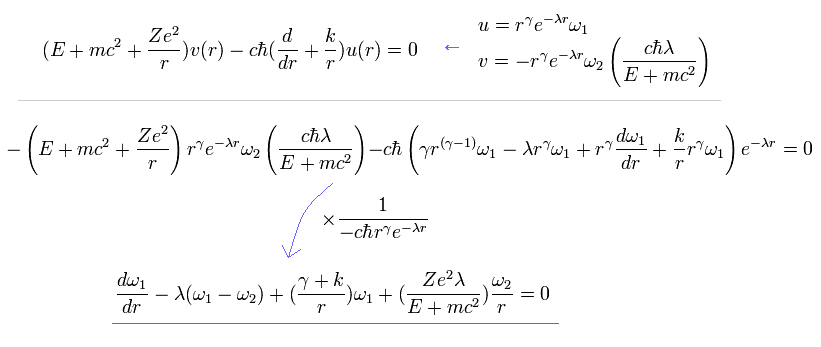
Here we define (using Eq.19 and Eq.23)
(Eq.29)
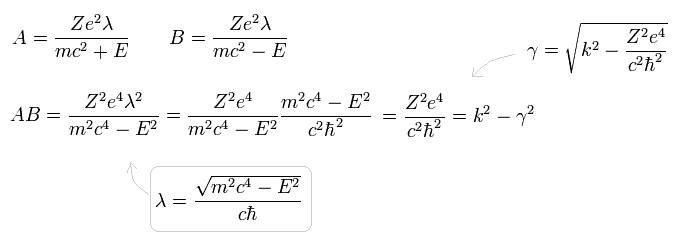
and replace r by x as follows,
(Eq.30)
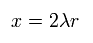
Using Eq.29 and Eq.30, Eq.28 become
(Eq.31)
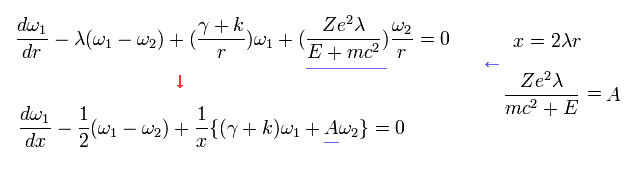
And Eq.27 becomes
(Eq.32)
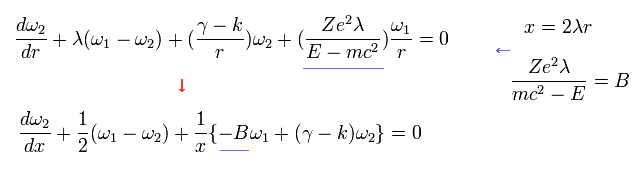
Here we expand ω1 and ω2 as follows,
(Eq.33)
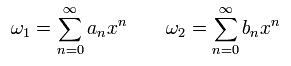
Substituting Eq.33 into Eq.31, coefficient of x to the power of n - 1 ( = xn-1 ) becomes,
(Eq.34)
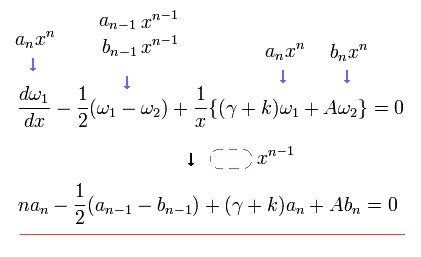
In the same way, substituting Eq.33 into Eq.32, the coefficient of xn-1 is
(Eq.35)
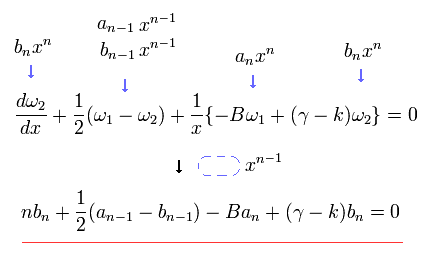
Summing Eq.34 and Eq.35, we obtain
(Eq.36)
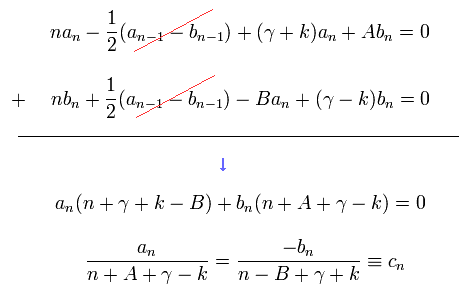
Substituting cn and cn-1 of Eq.36 into a and b of Eq.34, and using Eq.29, we get the relation of
(Eq.37)
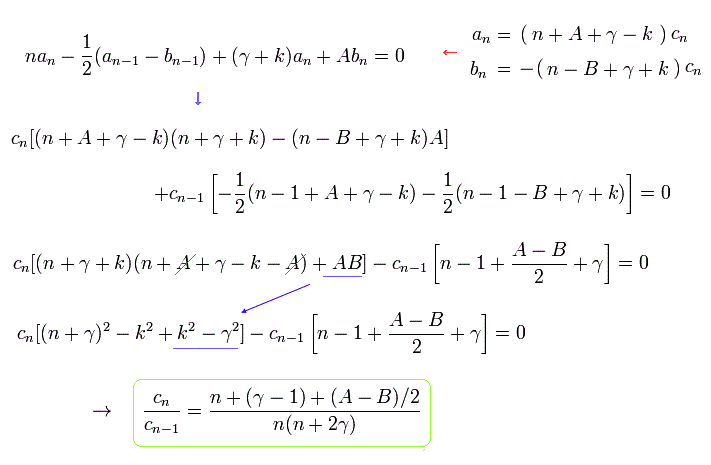
When we use the replacements of
(Eq.38)
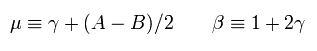
Eq.37 becomes
(Eq.39)
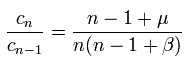
From the relation of Eq.39, we can define the function F(x) as follows,
(Eq.40)
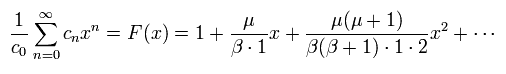
And using Eq.36, ω1 and ω2 (= Eq.33) can be expressed using the common cn,
(Eq.41)
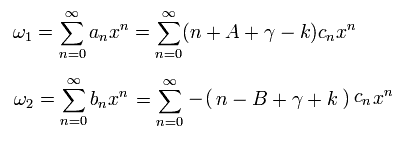
The power of cn is related to the energy level (= radial part ) of the hydrogen, as I explain later.
( This method is similar to Schrodinger's hydrogen. )
When F(x) is an infinite series, F(x) diverges exponentially at r → ∞ as follows,
(Eq.42)
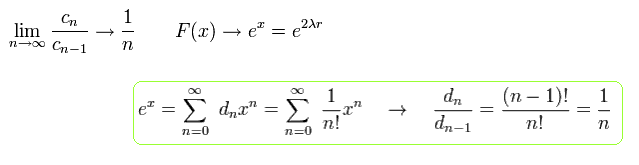
To make F(x) a finite series, μ of Eq.39 must satisfy ( this p.36-40 )
(Eq.43)
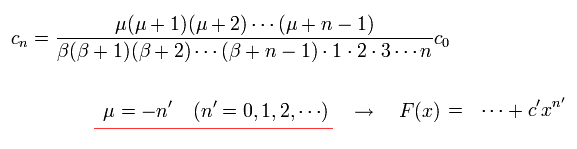
where F(x) becomes the nr th degrees with respect to x.
This nr is radial kinetic energy number (= freely chosen ) independent of other variables such as the total angular quantum number j.
From Eq.38,
(Eq.44)
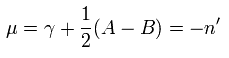
Substituting Eq.29 into Eq.44,
(Eq.45)
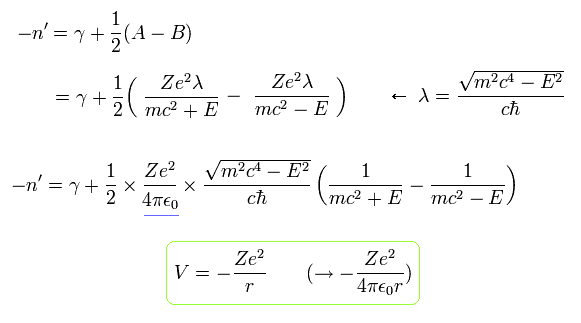
Here we return 4πε.
Using the fine structure constant α of Eq.26, Eq.45 becomes
(Eq.46)
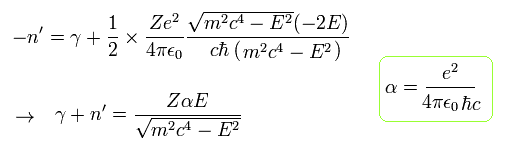
They define the new integer n (= energy level or principal quantum number ) as
(Eq.47) Dirac hydrogen's energy quantum number
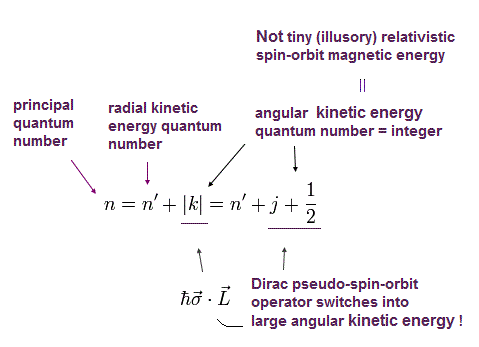
This n means the major energy level or the principal quantum number, nr is the radial (kinetic energy) quantum number, and |k| = J+1/2 is the angular momentum or kinetic energy quantum number which originates from the Dirac pseudo-spin-orbit interaction (= σL ) = relativistic spin-orbit magnetic interaction is illusion.
The energy E of Eq.46 becomes ( using Eq.25 and |k| = j + 1/2 )
(Eq.48) Dirac hydrogen's energy solution in 1928

where n means the principal quantum number ( this-last ).
And as shown on this page. this Dirac hydrogen energy values of Eq.48 ( this p.21, this p.9, this p.7 ) are completely consistent with those of Bohr Sommerfeld model of Eq.49 ( this p.12, this p.3-lower ).
(Eq.49) Bohr-Sommerfeld fine structure energy without spin in 1916 is right.
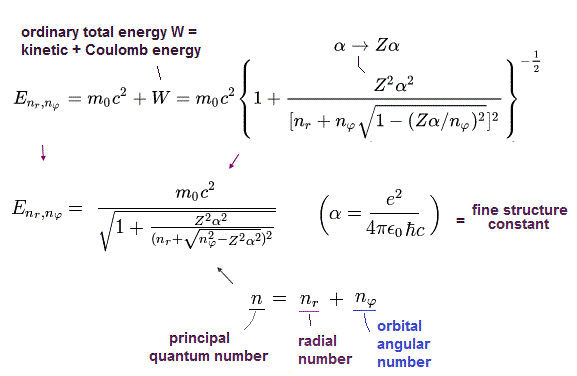
This means that the energy levels of them ( this-p.29 ) are just equal to each other, as follows,
Dirac 2p1/2 (n=2, j=1/2) -------- elliptic, (nr=1, nφ=1) Bohr-Sommerfeld
Dirac 2p3/2 (n=2, j=3/2) -------- circular, (nr=0, nφ=2) Bohr-Sommerfeld
↑ Dirac hydrogen's spin change from down to up (= j = 1/2 → j = 3/2 ) has as large energy impact as the change of orbital kinetic energy of Bohr-Sommerfeld's hydrogen (= nφ = 1 → 2 ) or non-spin Schrodinger's hydrogen.
This unnatural coincidence shows the later Dirac hydrogen copied the earlier successful Bohr-Sommerfeld fine structure result, even by making the electron's large angular kinetic energy look like a fake spin-orbit interaction (= σL ).

Feel free to link to this site.