トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。
特殊相対論は間違っている。
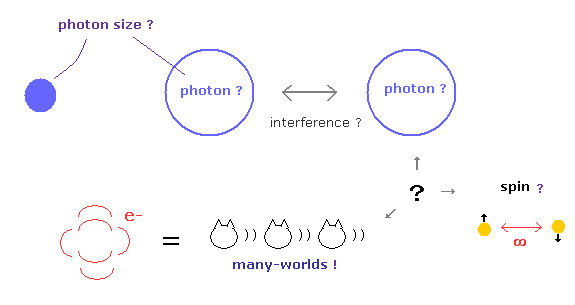
(Fig.1) 質問を許さない、 "Shut up and calculate !" 状態が続くと・・

あなたがたの中には 「 単一光子の 形や大きさは何なのか? 」、
「 スピン粒子は どのように不気味なリンクを感じるのか? 」、「 1s 軌道の電子は 本当に原子核に衝突しているのか? 」 などの素朴な質問をしたくなることがあるだろう。
しかし こういう素直な質問に対して 彼らはただ決まり切った文句 "Shut up and calcualte !" (= つべこべ聞かず黙って計算だけしてろ ) を繰り返すだけである。
驚くべきことに この異常な質疑応答状態が 100 年 もの長い年月に渡って 延々と続いているのである。
さすがに この異常状態が これほどの長期間続くと、様々な分野で 様々な深刻な問題、しわ寄せなどが 多数起こり得るのが自然だと思われないだろうか?
(Fig.2) 非現実的な ひも理論を信じないと物理界から阻害される = 異常状態。
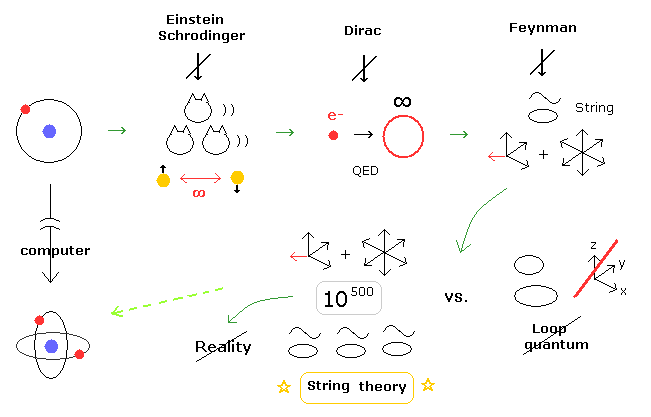
実際に 現在の物理の世界では 非実在的な 10 次元のひも理論に関して 激しい批判や 混沌とした状態が続いている。
例えば、もし 非現実的な ひも理論を信じないと 物理の世界では 阻害されるという具合にである。
( この状況は はっきり言って異常である。)
たとえ 実際に 特殊相対論が間違いであることを証明しても、彼らは 決して
QED、 標準模型、 一般相対論 (= ブラックホール、 加速膨張宇宙 ) などの相対論に関する理論を諦めようとしない。
実際の証明を無視することは この時点で これらのものは 科学ではなく 単なる信仰になってしまう。
また その致命的なパラドックスを隠して 学生たちに 相対論がからむ何らかのことを教え続けるとしたら、物理の教育に携わる人々に 重大な責任が生じると思われる。
( もちろん 重要なパラドックスを 相対論の教育者が知らなかったじゃ済まされない。)
(Fig.3) 反粒子は どのように粒子を区別して くっつくのか?
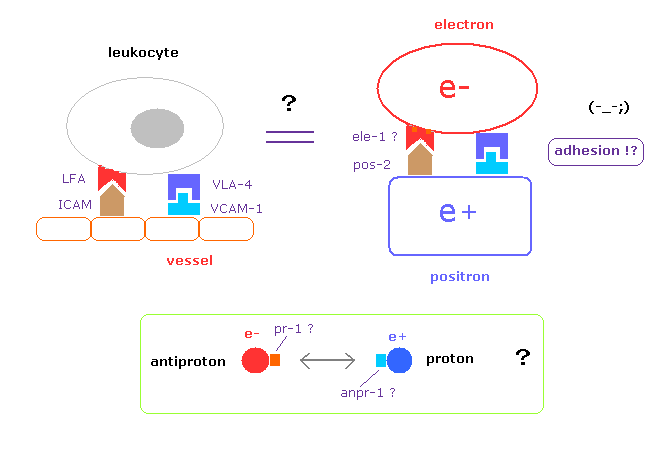
本当の科学の分野においては、例えば 白血球が血管に くっつき得ると分かった瞬間に どのような接着因子 ( LFA, ICAM-1 ) が そこに関わっているか調べるのが 自然の成り行きである。
しかし 彼らは 電子-陽電子間 もしくは 陽子-反陽子間 の 特異的な接着因子に関して 決して調べようとしない。
陽電子が発見されてから すでに 80 年もの歳月が経過しているにも関わらずだ。
このページに示したように、不安定な反粒子は 電子、陽子、中性子捕獲に自然に置き換えることが可能である。
また 非常に安定な電子のエネルギーが マイナスでなく プラス (= mc2 ) であることは不自然である。
これほど長期間にわたって 基本的な"質問をしない" ことは 彼らが これらの概念が 単なる 数学上の産物であると認めていることに等しい。
(Fig.4) 現在のバイオ技術は すでに その限界に達している。
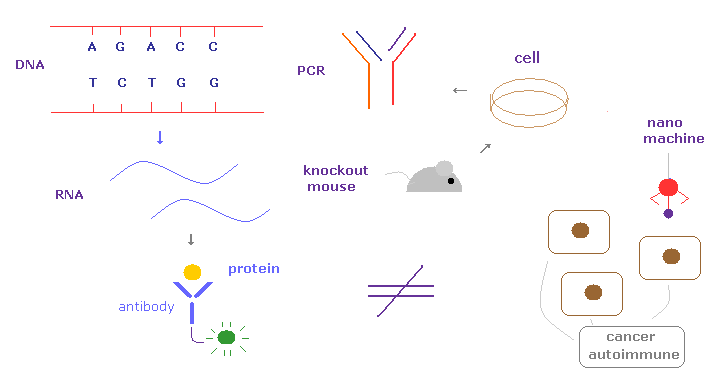
残念ながら 現在の DNA、RNA、培養細胞、抗体を用いたタンパク相互作用などの バイオ技術は すでに その限界に達している。
実際に 私たちが これらを用いて 癌、自己免疫疾患、ALS、認知症などの深刻な疾患を根治することは不可能である。
バクテリアなどに対する抗生物質などと異なり、これらの 癌、HIV、自己免疫疾患などは 私たち自身の組織から発生したものである。
そのため これらの疾患を治すには ナノ ( 電子 ) レベルで 様々な分子を見分け 操作できなければならない。
残念ながら 現在のバイオ技術などは マクロすぎて これらの疾患に対処できない。
これらに対処するには まったく役に立たない不確定性原理や 量子化学を諦めて 様々な電子の具体的な運動状態を知り かつ 制御できなければならない。
(Fig.5) C-C = 1.5400 Å は 釣り合いのとれた長さである。
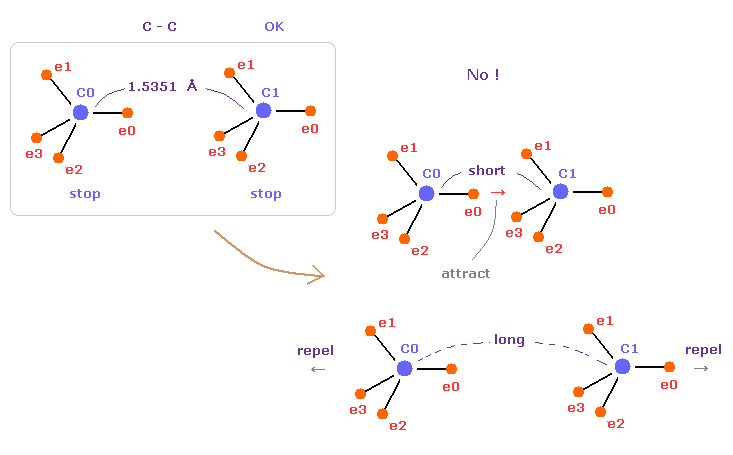
このページでは エタンの C-C 結合長が1.5351 Å になる理由を 力のバランスから説明することができた。
実は この結合長は 両方の C 原子核の安定性にとって 必要不可欠なものである。
もし C-C 結合長が 1.5351 Å よりも短くなると、e0 と C1 間の引力が 強くなりすぎる。
そして もし C-C 結合長が これよりも長くなると、2つの C 原子核間の反発力が優勢になる。
結果的に これらの状態は不安定になってしまう。
これが C-C 結合長を決定する 本当のメカニズムである。
サンプル JAVA プログラム もしくは
サンプルプログラム (text)
テキストエディタを "twoato.java" とセーブしてコンパイルしてほしい。 "--- Xlint : unchecked ---- " 等の注意は無視して実行できる。
(Fig.6) プログラム実行直後の画面 ( C-C )。
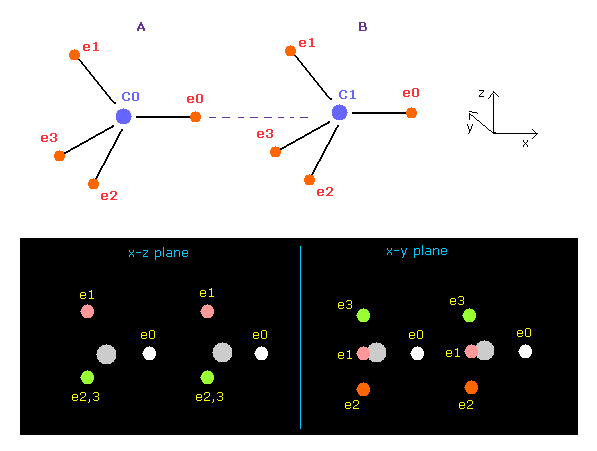
上記のプログラムを実行すると 画面には Fig.6 の電子配置が表示される。
このプログラムは スクロールバーの中より 水素、炭素、酸素、窒素、フッ素 の原子を選択して 様々な2原子の組み合わせを扱える。
Fig.6 の状態は 2つの炭素 (= C ) の 8つの価電子が 正四面体状に配置されており、それらの核間距離が 実験値 (= 15351 MM ) のケースである。ここでは 1 MM = 10-14 meter である。
中心の charge Z= 4.22 と nuc = 6415 は このページに示したように 炭素の 1-4 のイオン化エネルギーと "2.0" のドブロイ波長から得られたものである。
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | Waves |
|---|---|---|---|---|---|---|
| A ele 0 | 6415 | 0 | 0 | 6415 | 1673 | 2.000 |
| - ele 1 | -2138 | 0 | 6048 | 6415 | 2276 | 2.000 |
| - ele 2 | -2138 | -5237 | -3024 | 6415 | 2277 | 2.000 |
| - ele 3 | -2138 | 5237 | -3024 | 6415 | 2277 | 2.000 |
| B ele 0 | 6415 | 0 | 0 | 6415 | 1673 | 2.000 |
| - ele 1 | -2138 | 0 | 6048 | 6415 | 2276 | 2.000 |
| - ele 2 | -2138 | -5237 | -3024 | 6415 | 2277 | 2.000 |
| - ele 3 | -2138 | 5237 | -3024 | 6415 | 2277 | 2.000 |
| internuc (MM) | A 核への力 | B 核への力 | 力の差 | total V (eV) | Charge Z | nuc (MM) |
|---|---|---|---|---|---|---|
| C-C 15351 | FX = -340 | FX = -341 | = -1 | -596.7 | Z = 4.22 | 6415 |
"AB change" ボタンをクリックすれば、画面上のテキストボックス内に表示する電子の 原子 ( A か B ) を選択できる。
驚くことに、Table 1 に示したように、 C-C の核間距離が 実験値 (= 1.5351 Å ) のとき、A と B 原子核に作用する力の x 成分 (FX) は ほぼ同じ -340 と -341 になり、これは 安定した核間距離を意味している。
( 力の単位 1000 = ボーア半径離れた -e と +e 間に働く力。このページも参照のこと。)
ビリアル定理によれば、2つの 自由な炭素原子のポテンシャルエネルギーは -148.025 × 4 = -592.1 eV になる。
そのため Table 1 の結合エネルギーは ( 596.7 - 592.1 ) × 0.5 = 2.3 eV となり、この値は 実験値 3.5 eV (= 346 kl/mol ) に近い。
| C-C (MM) | A 核の FX | B 核の FX | その力の差 |
|---|---|---|---|
| 12000 | -856 | -1703 | -847 |
| 13000 | -633 | -1013 | -380 |
| 14000 | -479 | -627 | -148 |
| 15000 | -370 | -399 | -29 |
| 15351 | -340 | -341 | -1 ← |
| 16000 | -292 | -258 | +34 |
| 17000 | -234 | -168 | +66 |
| 18000 | -191 | -109 | +82 |
| 19000 | -158 | -69 | +89 |
C-C 核間距離 (MM) の値を 指定のテキストボックス内にいれて "internuc" ボタンをクリックすると、結合長を自由に変更できる。
Table 2 は A と B 原子核に作用する力の成分 FX の差を示したものである。
核間距離が短くなると、この違いは マイナスになる。
( これはつまり ますます核間距離が短くなり不安定になることを意味している。)
(Fig.7) C-C 結合長が実験値 = 1.5351 Å のとき。

C-C 結合長が実験値のとき、 A と B 原子核に作用する力は ほぼ 同じになる。
( FX = -340 と -341 ).
これはつまり C-C 結合長が 平衡状態で安定であることを示している。
また この結果は クーロン力と ドブロイの関係式が 実際の C-C 結合でも有効であることを示している。
(Fig.8) C-C 結合長が短くなると = 1.4000 Å
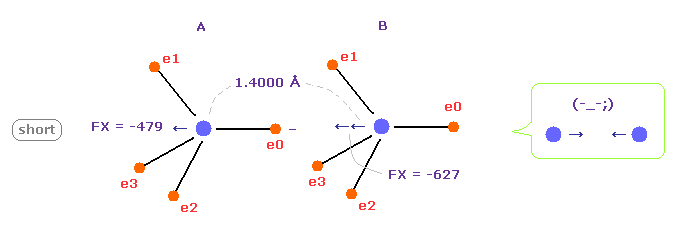
C-C 結合長が実験値より 短くなると (= 1.4000 Å )、 B の原子核は A 原子の 電子 e0 に 強く引かれすぎることになる。
これはつまり このケースでは C-C 結合長は さらに短くなろうとして不安定になってしまう。
(Fig.9) C-C 結合長が長くなると = 1.7000 Å
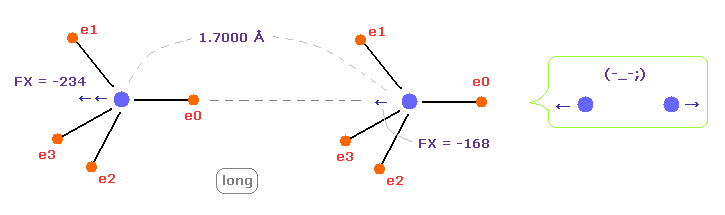
C-C 結合長が実験値より 長い (= 1.7000 Å ) とき、 2つの原子核間の 反発力が 強くなる。
これはつまり C-C 結合長が このケースでは不安定になってしまうことを意味している。
結果的に C-C 結合長が実験値のとき、その距離は安定になる。
(Fig.10) 上下の状態が交互に繰り返す。
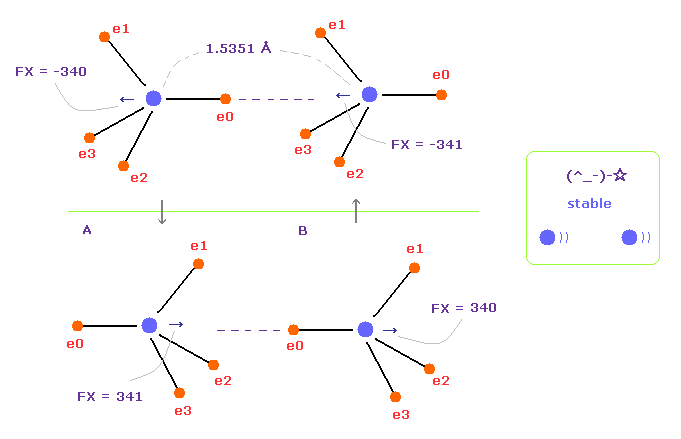
Fig.7 の全体の力は マイナス x 方向である。
しかし 価電子は 各原子核の周囲を運動しているため、Fig.10 の上下の状態を繰り返すことになる。
Fig.10 の上下の状態を足し合わせると、トータルの原子核に対する力は ほぼゼロになる。
プログラムでは、"180" の角度を指定のテキストボックス内に入力して "x-y ang" ボタンをクリックする。
すると、A 原子のすべての価電子が x-y 平面上で 180°回転する。
その後 "AB change" ボタンをクリックして B 原子に移り B 原子でも同様の回転を行う。
この状態が Fig.10 の下図の状態である。
C-C 結合長が長くなると、2つの原子核間の反発力が 必ず強くなってしまう。
また C-C 結合長が短くなると、引力が常に強くなってしまう。
(Fig.10') C では 正四面体構造が保たれる。
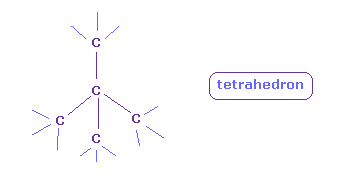
基本的に 炭素 (= C ) は ちょうど 4つの価電子を持つため その対称的な正四面体構造を保つことができる。
これらの正四面体構造では 正電荷と負電荷の粒子が 各 C 原子核周囲に均等に分布している。
この点が 酸素 ( H-O-H、O=O ) や フッ素 ( H-F ) と異なる点である。
そのため 4つの価電子が その構造を保つことができ、また 各炭素原子内のみで "2" ドブロイ波長について考慮することができる。
(Fig.11) C=C の結合長と結合角。

このページでは、エチレンの C=C 結合長と結合角を 古典的な軌道を用いて説明することができた。
このセクションでは、2つの炭素原子の関係のみの視点から これらの理由について考えることにする。
このプログラムを実行後、 A と B の両方の原子を x-z 平面で -54.7° 回転させる。
( -54.7 をテキストボックスに入力して "x-z ang" ボタンをクリックする。 )
この状態では ele0,1 は z 軸に平行、ele2,3 は y軸に平行になる。
(Fig.12) エチレンの結合長と結合角。
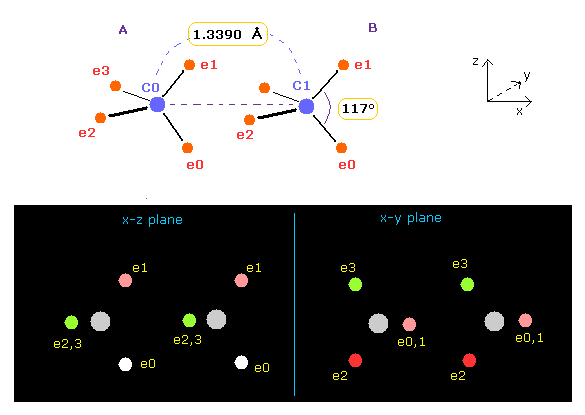
そして A 原子の ele 2,3 と B 原子の ele 0,1 のみを 対称的に移動させて 各原子核に作用する力 (FX) を ゼロに近づけさせる。
各電子と原子核間の距離は 定数とする。
( もちろん これらの仮定は 近似にすぎないが、だいたいの傾向はつかめる。)
| eNo. | +X (MM) | +Y (MM) | +Z (MM) | nuc (MM) | CF | Waves |
|---|---|---|---|---|---|---|
| A ele 0 | 3706 | 0 | -5235 | 6414 | 2162 | 1.976 |
| - ele 1 | 3700 | 0 | 5239 | 6413 | 2162 | 1.976 |
| - ele 2 | -3324 | -5487 | 0 | 6415 | 2272 | 2.023 |
| - ele 3 | -3324 | 5487 | 0 | 6415 | 2272 | 2.023 |
| B ele 0 | 3324 | 0 | -5487 | 6415 | 2272 | 2.023 |
| - ele 1 | 3324 | 0 | 5487 | 6415 | 2272 | 2.023 |
| - ele 2 | -3703 | -5237 | 0 | 6413 | 2162 | 1.976 |
| - ele 3 | -3703 | 5237 | 0 | 6413 | 2162 | 1.976 |
| internuc (MM) | A 核の FX | B 核の FX | total V (eV) | A e2-n-e3 | B e0-n-e1 |
|---|---|---|---|---|---|
| C=C 13390 | 0 | 0 | -594.36 | 117° | 117° |
Table 3 に示すように、A 原子の e2-nuc-3 の角と B 原子の e0-nuc-e1 の角が ちょうど 117° (= 実験値 ) のとき、各原子核に作用する力 (= FX ) は ちょうどゼロになる。
C=C 結合の反発力は C-C 結合よりも強いので 外側の価電子の間の角度は広くなる必要がある。
| C=C 結合長 | A e2 +X | - e2 +Y | - e2 +Z | A 核の FX | B 核の FX | A e2-nuc-e3 | B e0-nuc-e1 |
|---|---|---|---|---|---|---|---|
| 12000 | -3109 | -5612 | 0 | 0 | 0 | 122 deg | 122 deg |
| 12500 | -3201 | -5560 | 0 | 0 | 0 | 120 deg | 120 deg |
| 13000 | -3276 | -5516 | 0 | 0 | 0 | 118 deg | 118 deg |
| 13390 | -3324 | -5487 | 0 | 0 | 0 | 117 deg | 117 deg |
| 14000 | -3387 | -5449 | 0 | 0 | 0 | 116 deg | 116 deg |
| 15000 | -3459 | -5403 | 0 | 0 | 0 | 114 deg | 114 deg |
| 16000 | -3510 | -5370 | 0 | 0 | 0 | 113 deg | 113 deg |
Table 4 に示すように、C=C 結合長と 外側の結合角の間には明確な関係がある。
Table 4 は A 原子の e2 の座標のみを示している。
他の電子 ( A e3, B e0,1 ) は この e2 に対称的な位置に配置する。
ここでは 新しい単位 1 MM = 10-14 meter を使用している。
(Fig.13) エチレンの結合長と結合角。
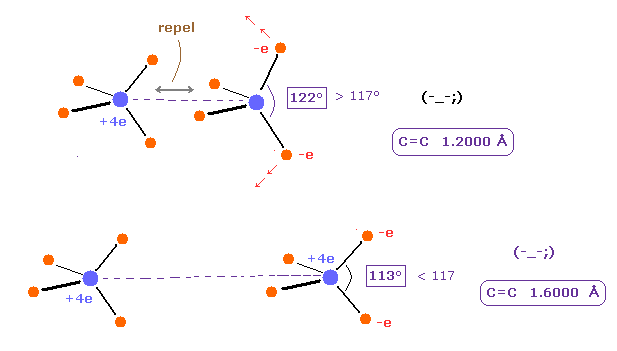
基本的に C=C 結合長が短くなるにつれて、2つの C 原子核間の反発力は 強くなる。
この反発力をキャンセルするために、外側の電子 ( A e2,3 と B e0,1 ) の間の角度は より 広くなる必要がある。
なぜなら これらの角度が広くなるにつれて、外方向への引力が弱くなるからである。
一方で、C=C 結合長が長くなるにつれて、C=C の反発力は弱くなる。
そのため 外側方向への引力は Fig.13 の下図のように 強くなる必要がある。
これが C=C 結合のメカニズムである。
( もちろん、現実の角度では e2-nuc-e3 の角度が広くなると、e0-nuc-e1 角度は少し小さくなる。 )
このページに示したように、ボーア軌道を用いて 水素分子を表すことに成功した。
このページでは このプログラムを用いて 水素分子に関して復習する。
プログラム実行後、A、B atom 両方において "H" を選択する。
H2 の核間距離は 0.7414 Å であるため、7414 を入力して "internuc" ボタンをクリックする。
(Fig.14) H2 分子。
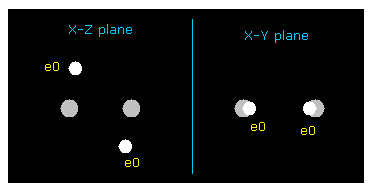
このプログラムでは、A と B 原子の両方において "ele 0" の x と z 座標を対称的に変化させる。
ele 1 は ele 0 に作用する力で 動いた後の 電子の座標である。 詳細は このページも参照のこと。
A と B 原子核の両方で安定 ( FX = 0 ) と 平均のドブロイ波が "1.0000" ( ave = 1.0000 ) であることを目指す。
| 核間距離 (MM) | A-X (MM) | A-Z (MM) | B-X (MM) | B-Z (MM) | 核への力 | ドブロイ波平均 | total V (eV) | 結合エネルギー |
|---|---|---|---|---|---|---|---|---|
| 6000 | 1870 | 4972 | -1870 | -4972 | 0 | 1.0000 | -60.664 | 3.120 |
| 6500 | 1145 | 4827 | -1145 | -4827 | 0 | 1.0000 | -62.204 | 3.890 |
| 7000 | 830 | 4755 | -830 | -4755 | 0 | 1.0000 | -62.893 | 4.234 |
| 7200 | 745 | 4739 | -745 | -4739 | 0 | 1.0000 | -63.014 | 4.295 |
| 7414 | 669 | 4729 | -669 | -4729 | 0 | 1.0000 | -63.056 | 4.316 |
| 7600 | 610 | 4724 | -610 | -4724 | 0 | 1.0000 | -63.047 | 4.311 |
| 7800 | 560 | 4721 | -560 | -4721 | 0 | 1.0000 | -63.010 | 4.293 |
| 8000 | 518 | 4720 | -518 | -4720 | 0 | 1.0000 | -62.952 | 4.264 |
| 9000 | 360 | 4741 | -360 | -4741 | 0 | 1.0000 | -62.365 | 3.971 |
H2 の平均の結合エネルギーは 最後の行 (= "bin" ) に示してある。
Table 5 の total V は 平均のポテンシャルエネルギーである。
Table 5 に示すように、H2 分子の結合長が 実験値 0.7414 Å (= 7414 MM ) のとき、 total V は もっとも低くなり、結合エネルギーは 最も高く (= 4.316 eV ) なる。
この値は 実験値 4.746 eV よりも少し小さい。
しかし この結果は H2 結合長が 0.7414 Å であることが 古典力学的観点から明らかに説明できたことを示している。
| 核間距離 (MM) | A-X (MM) | A-Z (MM) | B-X (MM) | B-Z (MM) | 核への力 | ドブロイ波平均 | total V (eV) | 結合エネルギー |
|---|---|---|---|---|---|---|---|---|
| 6000 | 1665 | 4878 | -1665 | -4878 | 0 | 0.9933 | -61.787 | 3.681 |
| 6500 | 1059 | 4745.5 | -1059 | -4745.5 | 0 | 0.9933 | -63.224 | 4.400 |
| 7000 | 775 | 4684 | -775 | -4684 | 0 | 0.9933 | -63.802 | 4.689 |
| 7200 | 697 | 4671.5 | -697 | -4671.5 | 0 | 0.9933 | -63.8815 | 4.728 |
| 7414 | 629 | 4662.3 | -629 | -4662.3 | 0 | 0.9933 | -63.916 | 4.746 |
| 7600 | 577 | 4658 | -577 | -4658 | 0 | 0.9933 | -63.899 | 4.738 |
| 7800 | 530 | 4657 | -530 | -4657 | 0 | 0.9933 | -63.838 | 4.707 |
| 8000 | 488 | 4657 | -488 | -4657 | 0 | 0.9933 | -63.765 | 4.670 |
| 9000 | 340 | 4681.5 | -340 | -4681.5 | 0 | 0.9933 | -63.125 | 4.350 |
次に このページに示したように1軌道のドブロイ波が 0.9933 のときを調べる。
Table 6 に示したように、H2 分子の結合長が 実験値 0.7414 Å (= 7414 MM ) のとき、 total V は 最も低く、結合エネルギーは 最も大きく (= 4.746 eV ) なる。
結合エネルギーの実験値は 4.746 eV である。
この結果は このページ と 真の H2 分子の結果と一致する。
つまり この簡略化した方法では ドブロイ波 = 0.9933 が 正しい標準値である。
もちろん、 上記の両方の基準において H2 の結合長 = 0.7414 Å が 最も安定になることには 変わりがない。
(Fig.15) 2つの H 原子が 完全に分離されている。
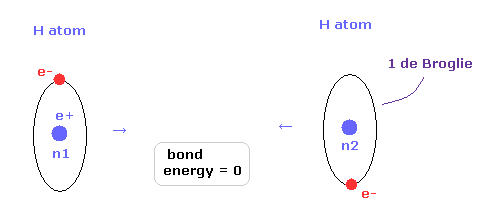
次に 核間距離が nuc = 7414 MM (= 実験値 ) のとき どうして H2 分子が最も安定になるのかという理由について考える。
Fig.15 では、2つの水素原子は 完全に分離しているため、結合エネルギーは ちょうどゼロである。
(Fig.16) 最も安定な H2 の形。
2つの原子核が互いに近づくにつれて、各電子は 2つの正の原子核と相互作用することができる。
そのため 結合エネルギーが大きくなり 安定な H2 分子が形成される。
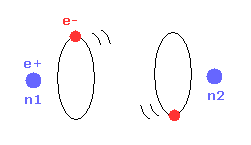
(Fig.17) 2電子間の反発力。

しかし 2つの電子が 実験値 7414 MM よりもさらに近づくと、2つの電子間の反発力が さらに強くなる。
結果的に "実質的"な中心電荷が小さくなる。
そのため 共通のドブロイ波の条件のもとで、半径 "r" は 大きくなり、結合エネルギーは 実験値よりも小さくなる 。
(Fig.18) 核間距離が短くなると・・
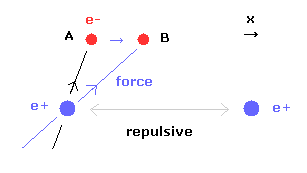
核間距離が短くなると、原子核間の反発力が強くなる。
この反発力をキャンセルするために、2つの電子は 中心方向に移動する必要がある。
電子1が x 方向に動くと ( A → B )、電子1による x 方向の引力が強くなる。
しかし この場合 Fig.17 に示すように 2つの電子間の反発力が強くなる。
このセクションでは、各原子 ( C, N, O, F, Si, P, S, Cl ) が どのように 他の原子の価電子を 引きつけるか 調べることにする。
最初に 炭素 (C) と ケイ素 (Si) のどちらが強いか調べることにする。
C-Si 結合長は 1.8500 Å である。 このプログラムを実行後 18500 を テキストボックスに入力後、 "internuc" ボタンをクリックする。
(Fig.19) C-Si 結合で e0 に作用する力。
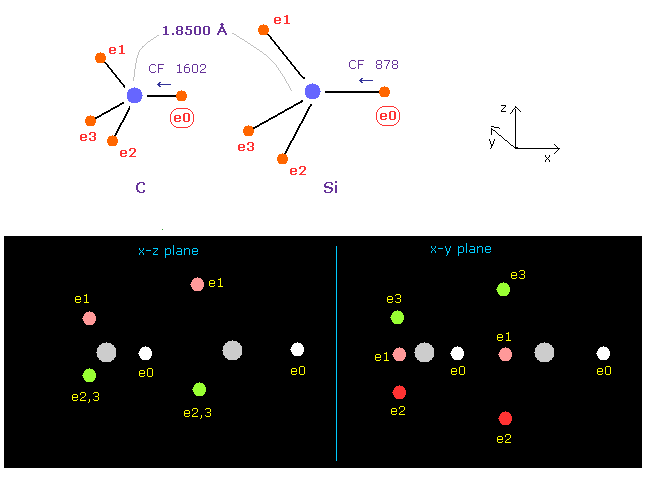
このページに示したように、1-4 のイオン化エネルギーと "3" ドブロイ波長を考慮すると、 ケイ素の電子の回転半径は 1.1500 Å で その中心電荷 Z = 5.05 である。
スクロールバーの中から "Si" を選んで "B atom" ボタンをクリックする。
それらの電気陰性度を比較するために e0 電子に作用する 原子核方向への力 (= CF ) の変化量を見る。
Fig.19 に示したように、炭素 (= A ) の e0 は CF 1602 で その原子核方向へ引きつけられており、ケイ素では CF は 878 である。
(Fig.20) C-Si 結合における e0 に作用する力。
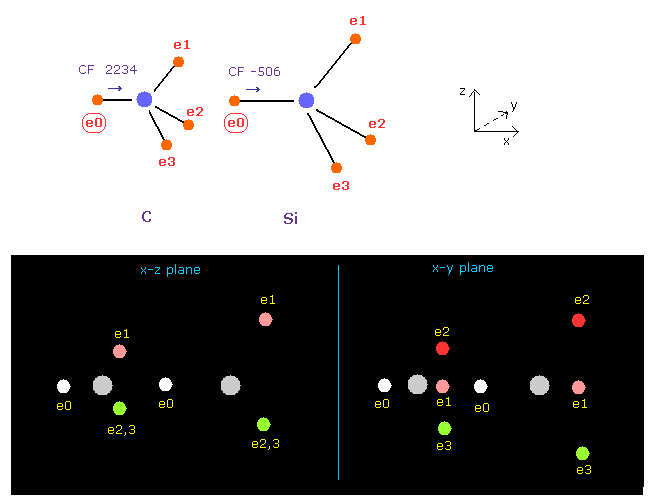
Fig.10 で述べたように、 2つの振動状態について考える。
A と B 原子両方において 180 の角度を指定のテキストボックス内に入力して "x-y ang" ボタンをクリックし、それらを回転させる。
Fig.20 では、 e0 の 力 CF は 炭素で 2234、ケイ素で -506 である。
このことは ケイ素は容易にイオン化され得ることを示している。
実際に 炭化ケイ素 ( SiC ) は 非常に希少な 結晶であり、単一分子としては存在しない。
また この炭化ケイ素は 絶縁体のダイアモンドと異なり 半導体である。
(Fig.21) 炭素の引きつける力が ケイ素より強い。

Fig.21 は Fig.19、Fig.20 を元に計算した 力 (= CF ) の変化と 元の力の比である。
たとえ 力の変化が大きくでも、元の力 (= 分母 ) が強ければ、その原子は 自身の電子を放出しにくい。
Fig.21 に示すように、一目で ケイ素の e0 電子が C 原子核に強く引きつけられていることが分かる。
これはつまり 炭素の引きつける力は ケイ素よりも強いということである。
実際に 炭素の電気陰性度 (= 2.55 ) は ケイ素 (= 1.90 ) のより大きい。
次に 炭素かリンのどちらが 引きつけ力が強いか調べることにする。
このプログラムを実行後、 スクロールバーで "P" を選んで "B atom" ボタンをクリックする。
( リンの Z と nuc は このページで得られたものである。 )
(Fig.22) 炭素 (C) - リン (P) 結合
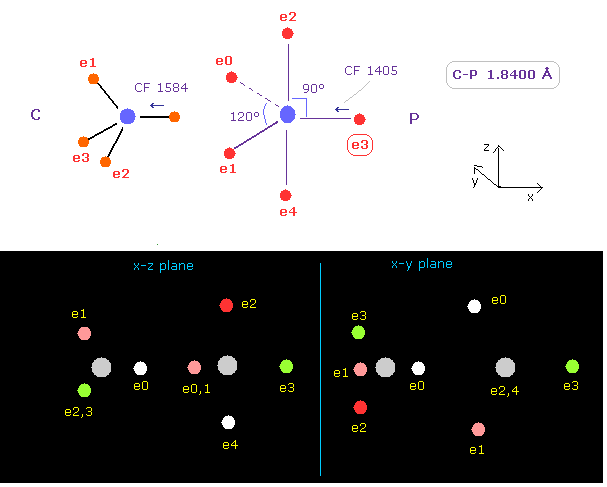
C - P 結合長は 約 1.8400 Å である。18400 をテキストボックス内に入力して "internuc" ボタンをクリックする。
Fig.22 に示したように、 原子核方向への力 (= CF ) は 1587 と 1405 である。
(Fig.23) C - P 結合 パート II.
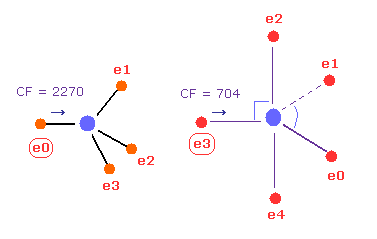
次に 角度 180 をテキストボックス内に入力して A と B 原子の両方において "x-y ang" ボタンをクリックする。
この状態では 力 CF は それぞれ 2270 と 704 である。
(Fig.24) 炭素の 引きつけ力は リンより強い。

Fig.22 と Fig.23 から、 各力の変化と 比を 計算する。
Fig.24 に示したように、力の変化は リンで大きい。
( これはつまり P の e3 電子は より C 原子核に引きつけられていることを意味している。)
つまり 引きつけ力は リンより 炭素のほうが強いことになる。
実際に 炭素の電気陰性度 (= 2.55 ) は リン (= 2.19 ) のより強い。
(Fig.25) 炭素 (C) - 硫黄 (S) 結合。

C - S 結合長は 約 1.8200 Å であるため 18200 を テキストボックス内に入力して "internuc" ボタンをクリックする。
Fig.20 に示したように、 C 原子の e0 で 原子核方向への力 (= CF ) は 1708 である。
(Fig.26) C - S 結合。 パート II.
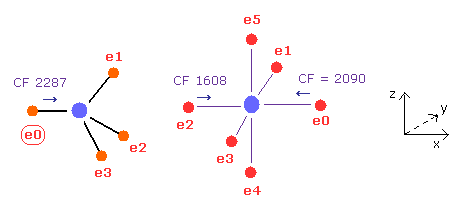
次に A 原子 (= 炭素 ) において 180 を入力して "x-y ang" ボタンをクリックする。
次に "AB change" ボタンをクリックして B 原子 (= S ) に移る。
B 原子において テクストボックス内に 45 を入力して "x-y ang" ボタンをクリックする。
炭素と硫黄は x-y 平面内で 指定の角度 回転する。
この状態では 力 CF は 炭素の e0 で 2287、硫黄ので 1608、 2090 である。
(Fig.27) 硫黄の引きつけ力は 炭素より強い。
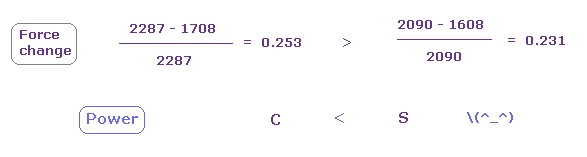
Fig.25 と Fig.26 から、 各力の変化と 比を計算する。
Fig.27 に示したように、力の変化は 炭素において大きい。
そのため 硫黄の引きつけ力は 炭素より少し強い。
実際に 硫黄の電気陰性度 (= 2.58 ) 炭素 (= 2.55 ) のより少し大きい。
( しかしそれらは 力と電気陰性度において ほぼ同じである。 )
次に 窒素と塩素のどちらの力が強いか調べることにする。
このプログラムを実行後、 スクロールバーから "N" を選んで "A atom" ボタンをクリックする。
そして スクロールバーから "Cl" を選んで "B atom" ボタンをクリックする。
( 塩素の Z と nuc は このページで得られたものである。 )
(Fig.28) 窒素 (N) - 塩素 (Cl) 結合。
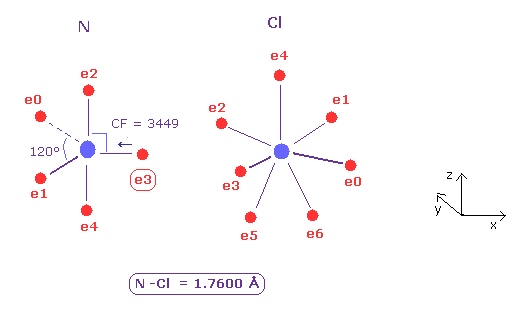
N - Cl 結合長は 約 1.7600 Å であるため、17600 をテキストボックス内に入力して "internuc" ボタンをクリックする。
Fig.28 に示したように、原子核方向への力 (= CF ) は N と Cl 原子で それぞれ 3449 と 2979 である。
(Fig.29) N - Cl 結合、パート II。
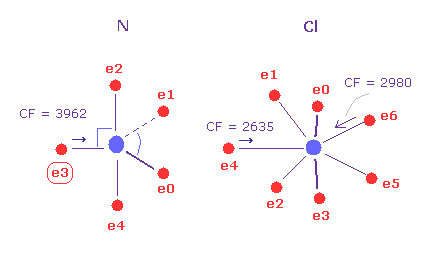
次に A 原子 (= 窒素 ) において 180 を テキストボックス内に入力して "x-y ang" ボタンをクリックする。
そして "AB change" ボタンをクリックして B 原子 (= Cl ) に移る。
B 原子で 角度 90 をテキストボックス内に入力して、"x-z ang" ボタンをクリックする。
窒素と塩素を 各平面内で指定の角度回転させる。
この状態では 窒素の e3 で 力 CF は 3962、 塩素で 2980 と 2635 である。
(Fig.30) 塩素の引きつけ力は 窒素より強い。
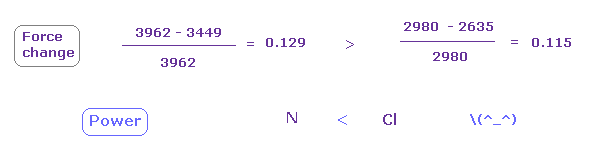
Fig.28 と Fig.29 から、 力の変化 と 比を計算する。
Fig.30 に示したように、力の変化は 窒素において少し大きい。
つまり 引きつけ力は 塩素のほうが窒素よりも少し強い。
実際に、塩素の電気陰性度 (= 3.16 ) は 窒素 (= 3.04 ) のよりも少し大きい。
(Fig.31) フッ素 (F) - 塩素 (Cl) 結合。
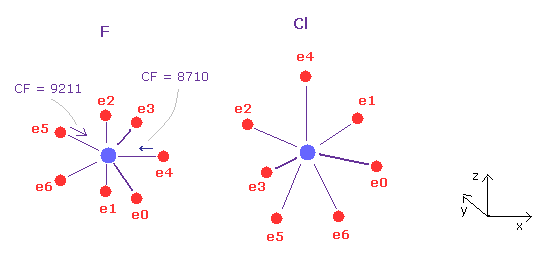
F - Cl 結合長は 1.6283 Å である。 よって 16283 をテキストボックス内に入力して "internuc" ボタンをクリックする。
Fig.31 に示したように、 原子核方向への力 (= CF ) は フッ素において 8710 と 9211 である。
(Fig.32) F - Cl 結合 パート II.
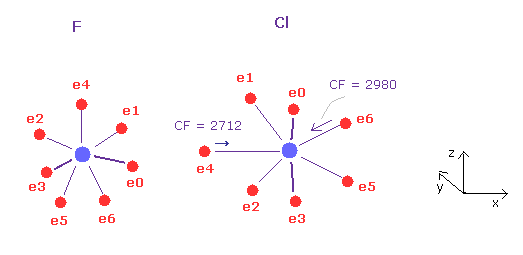
次に "A atom" ボタンをクリック ( F がスクロールバー内で ) して 元の状態に戻る。
"AB change" ボタンをクリックして B 原子 (= Cl ) に移り、角度 90 を入力して "x-z ang" ボタンをクリック。 (= Cl ).
この状態では 力 CF は 塩素において 2712 と 2980 である。
(Fig.33) フッ素の引きつけ力は 塩素よりも大きい。

Fig.31 と Fig.32 から、 各力の変化と比を求める。
Fig.28 に示したように、 力の変化は 塩素で大きい。
つまり 引きつけ力は 塩素よりフッ素が強い。
実際に フッ素の電気陰性度 (= 3.98 ) は 塩素 (= 3.16 ) よりも大きい。
フッ素の分子の力の変化は大きいが、フッ素は 最も強い引力を持つ ( 分母が 9211 ) ので 電気陰性度が強い。
結果的に 古典的軌道とドブロイ波を用いて 電気陰性度の本当の意味を説明することができた。
(Fig.34) 炭素の電子に作用する 力 (CF)。
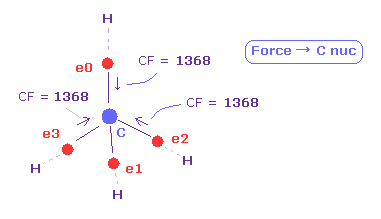
このページでは、メタン様の分子において 4つの炭素の価電子に作用する力について調べた。
メタンにおける CF (= 各電子に作用する力の C 原子核方向への力 ) は 1368 である。
この値は 妥当なものである。
(Fig.35) 力 = 1000.
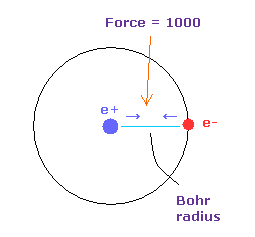
力の単位は Fig.35 に示したものである。
水素原子の基底状態で 電子と原子核間に作用している力を
"1000" とした。
つまり 電子と +e 原子核間の距離が ボーア半径のとき、 その力は 1000 になる。
例えば 力 1468 は H 原子の基底状態の 1.468 倍の力である。
| C-H 結合長 | CF ( Z = -0.4500 Å ) | CF ( 他の ele 1-3 ) |
|---|---|---|
| 0.9000 Å | -1383 | +1382 |
| 0.9500 Å | -121 | +1377 |
| 1.0000 Å | +636 | +1374 |
| 1.0870 Å | +1368 | +1368 |
| 1.1500 Å | +1660 | +1367 |
Table 7 は C-H 結合長に応じて 炭素の価電子 0 に作用する力 (= CF ) がどのように変化しているか表したものである。
C-H 結合長が 1.0870 Å (= 実験値 ) のとき、 力 CF は 約 1400 であり、この値は妥当である。
(Fig.36) 炭素の電子が (= e0 ) C の代わりに H に引きつけられる !?
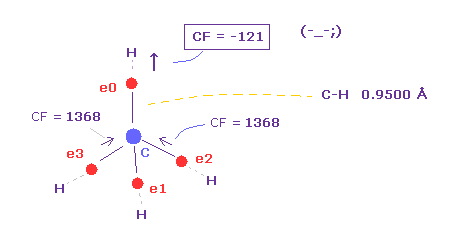
Table 7 に示したように、C-H 結合長が短くなると (= 0.9500 Å )、C 原子核方向への力は マイナスになる ( CF = -121 )。
これはつまり 炭素の価電子 e0 は C 原子核の代わりに 水素原子核に引きつけられることを意味している。
つまり このケースでは 電子と H 原子核が 不安定になってしまう。
C-H 結合長が 0.9500 Å のように短いと、 H 原子核をストップするために ドブロイ波は 1.000 に なれない。
C-H = 1.0000 Å においても、 CF = 636 は 小さすぎる値である。
( Fig.35 に示したように、 単純な水素原子においても 力は "1000" もある。 )
結果的に これら 価電子と原子核の 安定性が このページで述べたように メタンの C-H 結合長を 決定していることになる。
(Fig.37) フルオロメタン (= F-CH3 )。
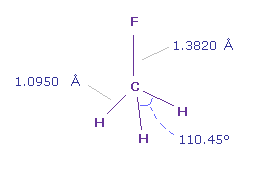
フルオロメタンの C-F 結合長は 1.3820 Å で、 C-H 結合長は 1.0950 Å である。
(Fig.38) 4つの価電子に作用する力は釣り合っている。.

このページに示したように、フルオロメタンにおいて 炭素の価電子に作用する力を調べた。
各電子の "CF" は 各電子に作用する力の C 原子核方向への成分を意味している。
( この CF を 周囲4つの原子からの 力のバランスとの判断材料とする。 )
Fig.38 に示すように、 F-C と H-C の結合長が 1.3820 Å、 1.0950 Å のとき、これらの力は ほぼ 互いに等しくなる。
F 側で CF = 1764 で、H 側で CF = 1417 である。
(Fig.39) 力のバランスが壊れる。

Fig.39 に見られるように、 F-C 結合長が短くなると (= 1.2000 Å )、炭素の価電子 "0" は フッ素原子核に 引きつけられすぎてしまう。
よって 他の CF = 1425 に比べて CF = 356 は 弱くなりすぎる。
( もちろん、このケースでは フッ素の原子核も この電子に引きつけられすぎる。 )
これはつまり これらの粒子は 上記の CH4 と同じメカニズムで 不安定になる。
| F-C 結合長 | e0 への力 | e1 への力 | e2 への力 | e3 への力 |
|---|---|---|---|---|
| 1.1500 Å | -644 | +1425 | +1428 | +1428 |
| 1.2000 Å | +356 | +1423 | +1425 | +1427 |
| 1.2500 Å | +985 | +1423 | +1425 | +1427 |
| 1.3820 Å | +1764 | +1417 | +1417 | +1422 |
| 1.4500 Å | +1935 | +1415 | +1415 | +1420 |
Table 8 にみるように、F-C 結合長が 実験値 (= 1.3820 Å ) より短くなると、炭素の価電子は フッ素に 引きつけられすぎてしまい 不安定になる。
F-C 結合長が 1.3820 Å のとき、e0-e3 における すべての力は 互いに ほぼ 等しくなる。
この現象は メタンとちょうど同じであり、結合長を決定する要因になっている。
このプログラムを実行後、 "C" (= 炭素 ) を "A atom" として選択する。
そして 様々な原子を "B atom" として選択して、それらの 炭素の電子 "ele 0" に対する影響について調べる。
(Fig.40) C の電子に作用する力の比較。
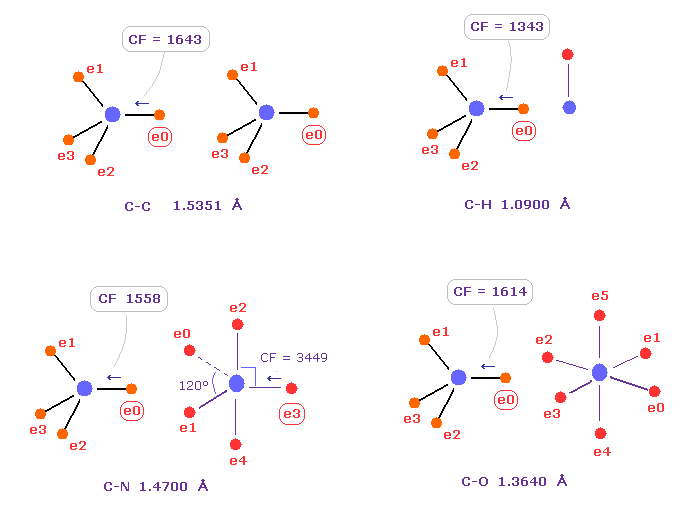
Fig.40 は C-C、 C-H、 C-N、 C-O のシングル結合における 力 CFを示したものである。
炭素が 様々な結合において 正四面体構造を 保っていることを考慮すると、炭素の電子に作用する力が 互いに ほぼ 等しくなるのが自然である。
実際に これらの力 (= CF ) は 異なった C-C、C-H、C-N、C-O 結合において それぞれ 1643, 1343, 1558, 1614 になる。
( これらの結合長は 実験値である、C-O の シングル結合は 酢酸からのものである。 )
| 分子結合 | 結合長 | e0 への力 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table 9 は 様々な結合における 炭素の電子 "ele 0" に作用する力 (= CF ) を示したものである。
驚くべきことに、異なった結合において、これらの力 (= CF ) は ほぼ 同じになる。
これはつまり 共通のメカニズムが働いて、炭素の正四面体の構造が 様々な結合において 保たれていることを示している。
(Fig.41) 様々な 酸素の結合長と結合角。

Fig.41 は 様々な酸素の化合物における 結合長と結合角を示したものである。.
基本的に Cl-O-Cl 角 (= 塩素 ) は 最も大きく、 F-O-F 角 (= フッ素 ) は 最も小さい。
( このページも参照のこと。 )
上で述べたように、フッ素は 最も強い引きつけ力を持つため、電子は フッ素のほうへ引きつけられて、O 原子核の F 側の電子密度が低くなる。
結果的に F-O-F 角は小さくなる。
しかし 塩素も 大きな引きつけ力を持つ。なら どうして Cl-O-Cl 角は H-O-H 角 (= 水 ) よりも大きいのだろうか?
ここでは H, F, Cl の O 原子核を 押す力の観点から これらの理由について考えることにする。
(Fig.42) O 原子核に対する 水素の押す力 (= FX )。
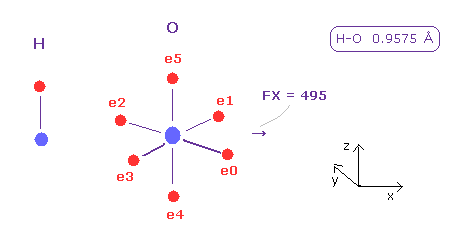
このプログラムを実行後、 スクロールバー内から "H" と "O" を選んで "A atom" と "B atom" ボタンをクリックする。
H-O 結合長は 0.9575 Å なので 9575 を入力して "internuc" ボタンをクリックする。
Fig.42 では O 原子核に作用する力の x 成分が FX = 495 である。
もちろん、これらの力をキャンセルするために 各電子を動かす必要がある。しかし どれぐらいの力で 互いに押し合うか だいたいの傾向は掴める。
水素原子は その電子軌道が 1 × ドブロイ波長なため 自身の電子を保持したまま 他の原子核に近づくことができる。
(Fig.43) O 原子核に対する フッ素の 押す力 (= FX )。
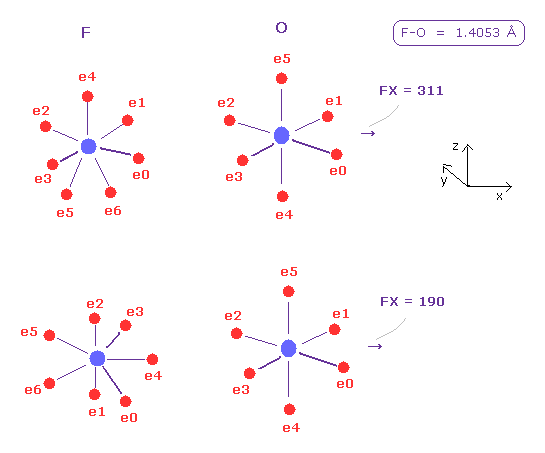
次に "F" を選んで "A atom" ボタンをクリックする。
F-O の核間距離は 1.4053 Å である。そのため 14053 を入力して "internuc" ボタンをクリックする。
この状態 (= Fig.43 上図 ) では、 O 原子核に作用する力の x 成分は FX = 311 である。
この押す力は 水素 ( FX = 495 ) のよりも 小さい。なぜなら フッ素は 7つもの価電子を持ち、かつ その回転半径が小さいからである。
次に -90 の角度を入力して "x-z ang" ボタンをクリックして フッ素を回転させる。
この状態 (= Fig.43 の下図 ) においても、 FX = 190 は小さい。
結果的に O 原子核を押す力の観点からも、 O 原子核の安定性のために、F-O-F 角は H-O-H 角よりも小さくなる必要がある。
(Fig.44) O 原子核に対する 塩素の押す力 (= FX )。
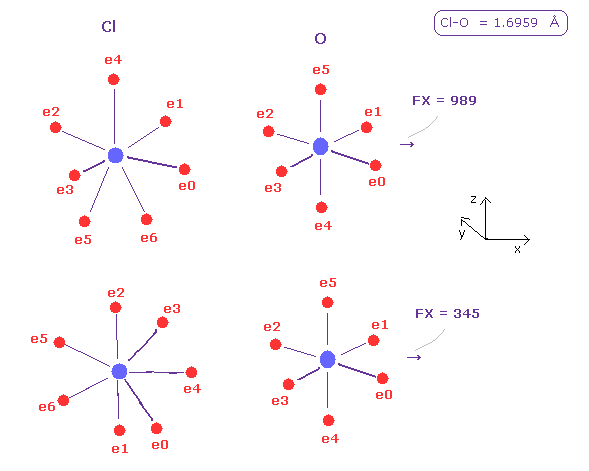
同様に internuc=1.6959 にして、A 原子を 塩素 ( Z = 8.26, nuc= 7640 ) に変える。
酸素原子核に対する 塩素の押す力の合計は 大きい, ( 989 + 345 ) × 0.5 = 667。
もちろん、塩素の価電子は Cl 原子核自身から より離れているため、フッ素よりも O 原子核に より容易に引きつけられる。
そのため これらの反発力がキャンセルされる傾向にある。
しかし Cl の価電子の 広範囲の電子分布のために、塩素は 大きな反発力を持つ。
そのため Fig.42 において O 原子角の安定のために Cl-O-Cl 結合角は大きくなる必要がある。
(Fig.45) どうして H-S-H 結合角は小さいのか?
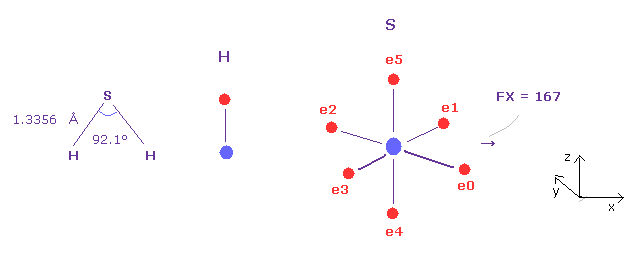
H-S-H 結合角 (= 92.1° ) は H-O-H (= 104.5° ) よりも小さい。
この理由を 押す力の観点から説明できる。
H と O を A、B 原子に選び、 電荷 Z = 7.18、 nuc = 8622 を B 原子に選んで 硫黄に変更する。
そして 核間距離を 1.3356 Å (= 13356 MM ) にする。
Fig.45 に示したように、S 原子核に対する 押す力 FX = 167 であり、この値は Fig.42, Fig.43, Fig.44 に比較して 最も小さい。
そのため S 原子核の安定のために H-S-H 角は小さくなる必要があり、正八面体の 90°により近づく。
(Fig.46) 炭素における 様々な結合長
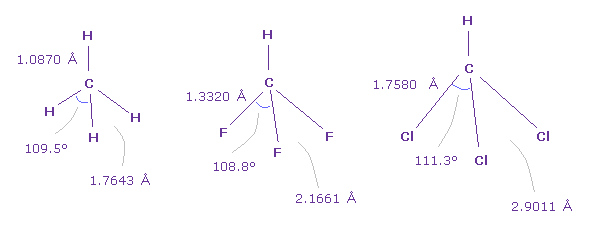
実際に CH4 (= メタン )、 HCF、HCCl3 においても、 F-C-F 角は最も小さく、Cl-C-Cl 角は 最も大きい。
また Fig.34 の F-F 結合長 (= 2.1661 Å ) は Fig.42 の F-F 結合長 (= 2.1996 Å ) に非常に近い。Fig.29.
また Fig.46 の Cl-Cl の長さ (= 2.9011 Å ) も Fig.42 の Cl-Cl の長さ (= 2.7936 Å ) に非常に近い。
これらの結果は 様々な異なった分子において 共通のメカニズムが働いていいることを示している。
(Fig.47) C=C における様々な結合角。
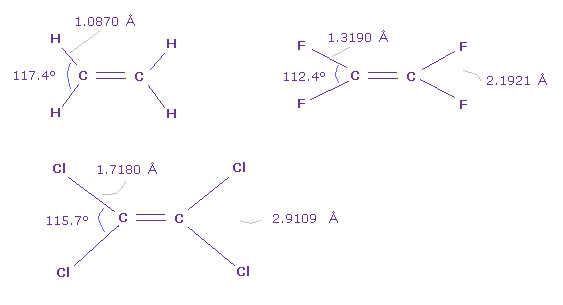
Fig.47 では、 H-C-H 角は 最も大きく、 F-C-F 角が最も小さい。
しかし Fig.46 と Fig.47 を比較すると、 Cl-Cl の長さは ほぼ等しい ( 2.9109 Å = 2.9011 Å )。
また Fig.13 の力のバランスを考慮すると、結合角が小さくなるにつれて、炭素の外側の2つの価電子が C 原子核を引きつける傾向になる。
Cl-O-H や F-O-H の分子では、これらの結合角は小さく、それぞれ 102.5°と 97.2°である。
これらのケースでは、水素原子、塩素、フッ素 ( H-Cl、H-F ) は Cl-Cl もしくは F-F よりも より互いに引き合う傾向にあるからである。
(Fig.48) 水素 (H) - 炭素 (C) 結合。
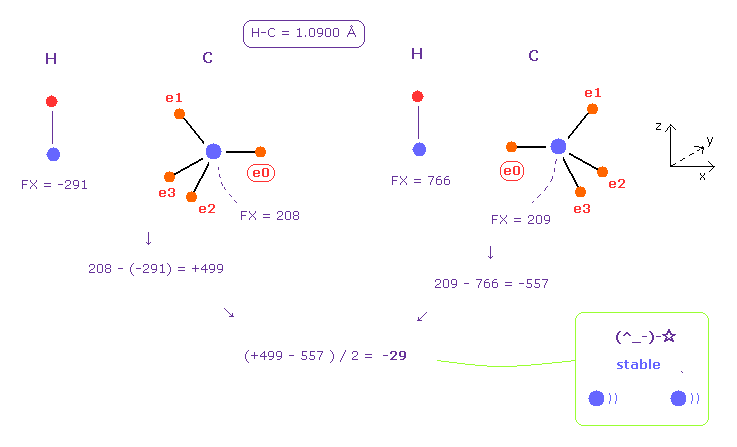
このプログラムを実行後、 A と B 原子 として H と C 原子を選ぶ。
基本的に 炭素の電子は、2つ以上のパターンで運動している。
Fig.48 の左は 2つの原子核間の反発力 (= +499 ) を意味している。
右は 引力 (= -557 ) である。
( 右図は 炭素を 180°、 x-y 平面で回転させて得られる。)
それらを合計して 2で割ると、平均の力 -29 が得られ これは ほぼゼロである。
これはつまり 水素の電子は 炭素の原子核に そんなに近づく必要はないことを意味している。
( そのため 水素結合、 C ---- H-C は 形成されにくい。)
(Fig.49) 水素 (H) - 窒素 (N) 結合。
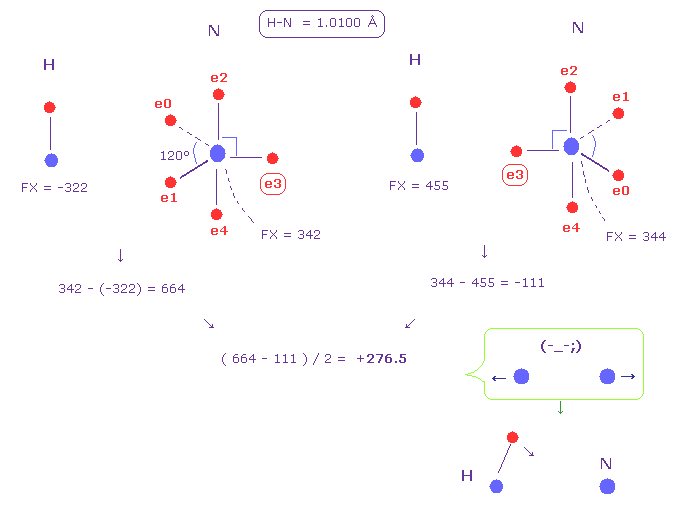
Fig.49 は H-N 結合を示している。
Fi.48 のように、2つの原子核間の平均の力
なぜなら Fig.49 では、水素の電子を固定した状態に仮定したからである。
この結果は この反発力をキャンセルするために 水素の電子は 他の原子核に引きつけられる必要があることを示している。
このことが 水素を正に分極させ 水素結合を生じさせる ( N ---- H-N )。
(Fig.50) 水素 (H) - 酸素 (O) 結合。

Fi.50 は H-O 結合を表している。
Fig.48 のように、2つの原子核間の平均の力 +454.5 (= 反発力 ) を得た。
この結果は 水素の電子は この反発力をキャンセルするために より他の原子核に引き寄せられる必要があることを示している。
このことが 水素を正に分極させ 水素結合を生じさせる ( O ---- H-O )。
(Fig.51) 水素 (H) - フッ素 (F) 結合。
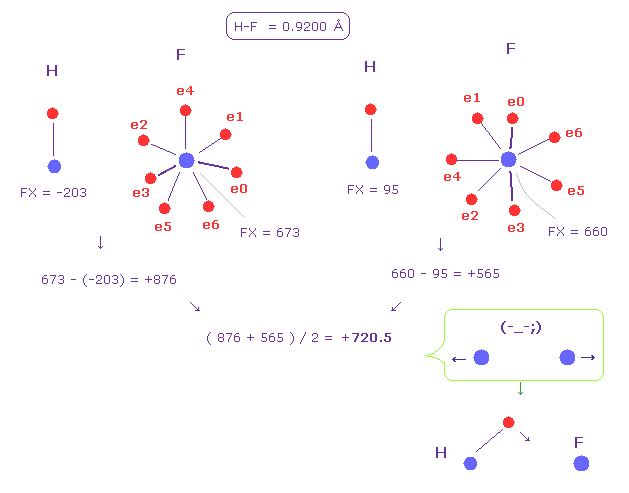
Fi.51 は H-F 結合を表している。
Fig.50 のように、2つの原子核間の平均の力 +720.5 (= 反発力 ) を得た。
この結果は この水素の電子は この反発力をキャンセルするために 最も 他の原子核に引き寄せられる必要があることを示している。
これが 水素のイオン化を引き起こす。
上記のプログラムを実行して H-F 結合を調べると、フッ素の引きつける力が強すぎるため 水素のドブロイ波が短くなりすぎてしまう。
そのため 電子は フッ素原子核に かなり近づく必要がある。
実際に フッ化水素は 結晶様の気体で、単体の H-F では存在しない。
| H - A 原子 | 電荷 Z | 半径 | 結合長 | 核間力-1 | 核間力-2 | その平均の力 | A の 電気陰性度 |
|---|---|---|---|---|---|---|---|
| ケイ素 (Si) | 5.05 | 11500 | 14800 | +433 | -2000 | -783 | 1.90 |
| リン (P) | 6.12 | 9825 | 14400 | +476 | -670 | -97 | 2.19 |
| 炭素 (C) | 4.22 | 6415 | 10900 | +499 | -557 | -29 | 2.55 |
| 硫黄 (S) | 7.18 | 8622 | 13400 | +496 | -370 | +63 | 2.58 |
| 窒素 (N) | 5.25 | 5331 | 10100 | +664 | -111 | +276 | 3.04 |
| 塩素 (Cl) | 8.26 | 7640 | 12700 | +635 | -60 | +287 | 3.16 |
| 酸素 (O) | 6.273 | 4596 | 9600 | +661 | +258 | +454 | 3.44 |
| フッ素 (F) | 7.3 | 4003 | 9200 | +876 | +565 | +720 | 3.98 |
A 原子の電子の 回転半径と 結合長は 単位 1 MM = 10-14 meter = 0.0001 Å で表している。
中心電荷 Z と 各原子の電子の回転半径は このページで得られたものである。
核間力-1 は パターン-1 ( 例えば Fig.48 の左図 ) における 2つの核間の力である。
この値は 2つの FX 間の違いであり、これが正だと 反発力を意味する。
核間力-2 は パターン-2 ( 例えば Fig.48 右図 ) のものである。
平均の力は この2つを足して2で割ったものである。
Table 10 に示したように、H-C ( 炭素 ) 結合では、2つの核間の力は ほぼゼロになる。
なぜなら 水素の電気陰性度 (= 2.20 ) は 炭素 (= 2.55 ) に近く、また H-C 結合は 基本的に安定で イオン化や分極をしないからである。
(Fig.52) H 電子は F に引き寄せられる。

ケイ素は 非常に弱い電気陰性度を持つため、ケイ素の電子は 水素原子核に引きつけられすぎて、これがイオン化を引き起こす。
電気陰性度が強くなるにつれて、2つの核間の反発力が強くなる。
( なぜなら すべてのケースで 水素の電子を固定したからである。)
そのため A の原子の電気陰性度が強くなるにつれて H の電子は 他の原子核のほうへ より引きよせられる必要がある。
( これが 水素の正の分極を生じる。)
Table 10 は 平均の力と A 原子の電気陰性度の間に 非常に良い相関関係があることを示している。
(Fig.53) "先端の" 電子 (= e0 ) は 互いに避け合う。
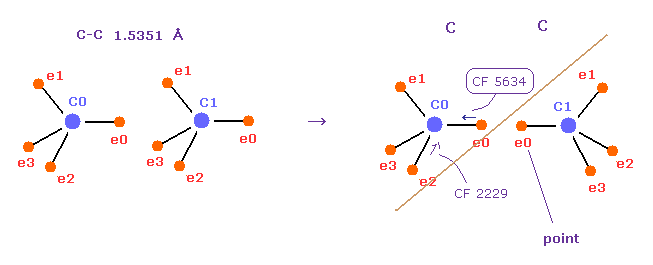
基本的に C-C 結合では、炭素の価電子は 他の炭素の価電子を避けながら 周期的に運動している。
Fig.53 は 炭素-炭素 ( C-C ) 結合である。
実際に 右図では、各先端の電子を互いに向かい合わせようとすると CF (= 中心方向への力 ) は 反発力によって 2229 から 5634 へ急激にに上昇してしまう。
(Fig.54) C-Cl 結合の 先端電子は C-C よりも互いに近づける。

一方で C-Cl 結合では 塩素と炭素の先端の電子は その長い結合長 (= 1.7700 Å ) のために互いに向き合っている。
実際に、CF は 2280 から 3262 に上昇しているが それは 上記の C-C のときよりも小さい。
もし Cl が 炭素方向を向いていないとしたら、炭素の原子核は Cl の強い正電荷のために 反発される。
( 下図、FX = -590 ).
なぜなら 塩素の7つの価電子は 非常に広く広がっているからである。
しかし Cl が C 原子核の方向を向いていると、FX は小さくなる ( 上図、FX = -260 )。
Cl の強い反発力をキャンセルするために、それらは 先端の電子を互いに向け合う必要がある。
そうするには、ある程度の長い距離が必要になってくる。
(Fig.55) C 原子核に作用する力は似ている。
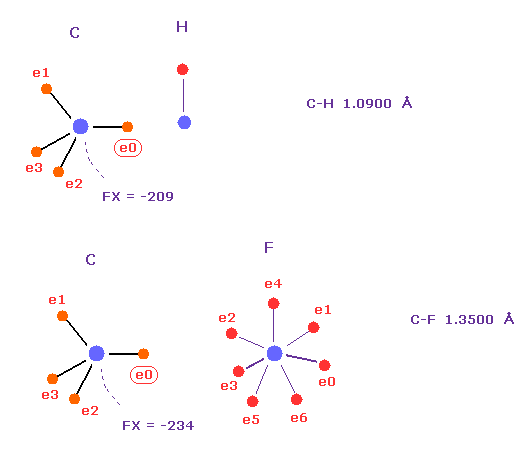
Fig.54 の C-Cl 結合の炭素に作用する力 ( FX=-260 ) は C-H ( FX = -209 ) もしくは C-F ( FX = -234) 結合のものと近い。
もちろん、もっとより安定な状態を探すため それらの位置を少し修正する必要はある。
(Fig.56) 炭素における様々な結合角。

水素、フッ素、塩素は メタン様の構造を形成するため、これらの似た FX の値は合理的である。
また 上で述べたように、塩素は その非常に広く広がった価電子のために かなり強く正電荷の性質を発揮しているため、Cl-C-Cl 結合核は それらの中で最も大きい。

2013/4/13 updated This site is link free.