トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは現実には存在しない。
特殊相対論は間違い。
(Fig.1) 分子軌道法は ビリアル定理に反する。

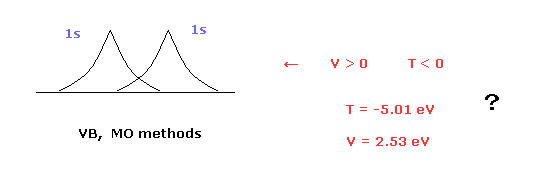
原子価結合法 ( VB ) と 分子軌道法 ( MO ) は 水素分子 (H2) に対する量子力学的手法の代表格である。
これらの量子力学的手法では 2つの 1s の水素原子の波動関数が H2 分子として用いられている ( このページも参照のこと。)
( H2 結合エネルギー計算結果 VB = 3.14 eV と MO = 2.68 eV は 実験値 (= 4.74 eV ) と異なる。 )
問題は これらの手法は ビリアル定理に反するということである。
なぜなら これらの量子力学的な H2 分子は 負の運動エネルギー (= T ) と 正の位置エネルギー (= V ) を持つからである。
これらの問題は 1960年代頃から知られていた。
(Fig.2) 量子力学のヘリウム原子 ?

このページに示したように、量子力学的な変分法は 系が2つ以上の電子を含んでいるとき 正確なエネルギー値を与えることができない。
このケースでは、彼らは 電子間距離 (= r12、 Fig.2 ) の変数を含む波動関数を使用している。
例えば、Fig.2 では ヘリウムの2つの電子が 互いに近づくにつれて 波動関数の振幅は小さくなる。
これも 人為的な操作の1つである。
(Fig.3) 電子間距離の操作。

Fig.3 では、 電子間距離 r12 が "1" より小さくなると、波動関数の振幅は小さくなる。
そのため r12 = 1 の状態を 人為的に選ぶことができる。
量子力学的なヘリウムと水素分子 (H2) の変分法は 完全にこれらの技巧に依存している。
また これらの模型は ヘリウムと H2 分子の2つの電子が 他の電子を避けながら、 明らかに運動していることを示唆している。
最初に ボーア軌道に基づく H2 分子模型について調べることにする。
このページを読まれていないときは 最初に読まれるように。
(Fig.4) 推定される H2 分子。
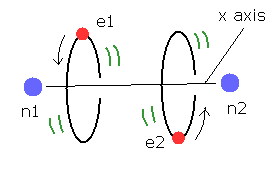
核間距離 ( 0.7414 × 10-10 m ) と 2つの電子と原子核間のクーロン相互作用を考慮すると、H2 分子の実際の電子状態は Fig.4 のようになると考えることのは自然である。
もちろん、クーロン相互作用は 量子化学においても もっとも重要な概念ある。
また 分子の形を決定する他の重要な概念が ドブロイ波長である。
(Fig.5) もし ドブロイ波長が存在しないと?
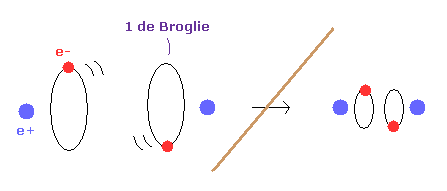
もし ドブロイ波長の概念がないと、水素原子の電子軌道は ゼロにまで小さくなれる。
結果的に H2 分子の核間距離は 好きなだけ短くなることが可能である。
なぜなら 2つの核間の反発力が 任意に小さな電子軌道によってキャンセルされるからである。
つまり ドブロイ波長の概念によって H2 の核間距離 ( 0.7414 × 10-10 m ) が保たれていることになる。
(Fig.6) H2 では 原子核と電子の両方が安定になる必要がある。

分子が ある核間距離で安定になるとき、それらの原子核と電子軌道の両方が安定になる必要がある。
このページでは、H2、CH4、H2O などの様々な分子において それらの核間距離が実験値でないとき、電子もしくは原子核が不安定になることを示す。
(Fig.7) H2 分子。
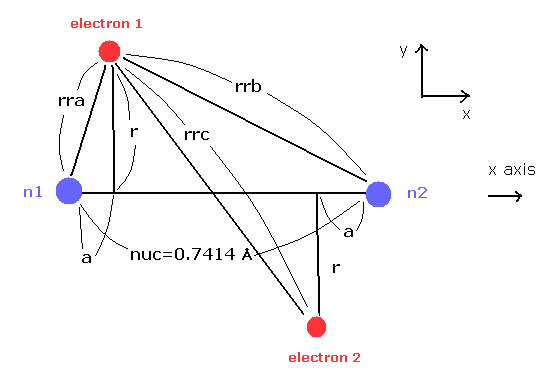
ここでは Fig.7 の模型を用いて 1軌道中のドブロイ波の数を 次のプログラムに従って計算する。
H2 分子の サンプル JAVA プログラム。
H2 分子の C 言語プログラム。
ここでは 新しい単位 1 MM = 1 × 10-14 meter を使用している。
このプログラムでは、最初に H2 の核間距離 (= nuc, MM ) を入力する。
その後、電子1の y座標 "r" ( MM )、x 座標 "a" ( MM ) を 入力する。
(Fig.8) ( a, r ) における様々な力。
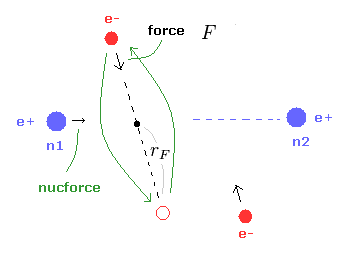
これら入力値から、このプログラムは H2 の結合エネルギー (eV)、原子核 1 に作用する トータルの力 (= nucforce )、電子1に作用する力の x, y 成分 (= elefx, elefy ) を出力する。
これらの力は 水素原子の基底状態の電子と原子核間の力との比で表されている。
(Fig.9) e1 に作用する 力 F。
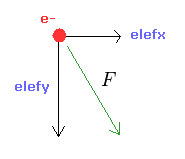
入力値 ( a, r, nuc ) より、全位置エネルギー V を計算する。
ビリアル定理を用いて、全エネルギー E = 1/2 V と 運動エネルギー T = -1/2 V を得る。
この運動エネルギーより、電子速度 (= v ) と ドブロイ波長 (= h/mv ) を計算する。
(Eq.1) F = 遠心力。
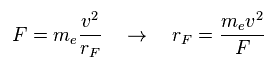
ここでは 力 F を 遠心力と仮定する。
Eq.1 の関係式から 回転半径 (= rF ) を得ることができる。
(Eq.2) 1軌道のドブロイ波
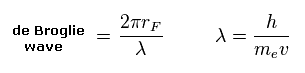
ドブロイの関係式 ( λ = h/mv ) を用いて、1軌道 (= 2πrF ) に含まれるドブロイ波の数を計算する。
ビリアル定理を用いて、位置 ( a, r ) における H2 分子の 結合エネルギーを計算する。
(Fig.10) 電子の もう1つの x 座標。
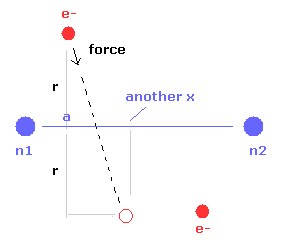
また このプログラムは Fig.10 に示すように 電子1が 力 F の方向へ動いたときの もう1つの x 座標 ( MM ) を出力する。
この x 座標は 電子の x 方向への揺れの指標になる。
さらに another x の位置における 電子のドブロイ波と 電子に作用する力を計算する。
そして 1軌道中の 平均の結合エネルギーとドブロイ波 (= Table 1 ) を出す。
なぜなら 電子軌道は 横方向に揺れているため、それらの平均値を出す必要があるからである。
最初に 結合エネルギー (= 4.746 eV ) と 核間距離 (= 0.7414 × 10-10m = 7414 MM ) が 実験値のケースについて考える。
(Eq.3) H2 の実験値。
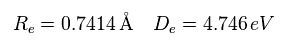
電子1が ( a = 629 MM, and r = 4662 MM ) にあるとき、原子核に作用する 力の合計はゼロになる。
( nucforce = 0。 この地点で 2つの原子核は 安定になる。 )
(Fig.11) 実験値。
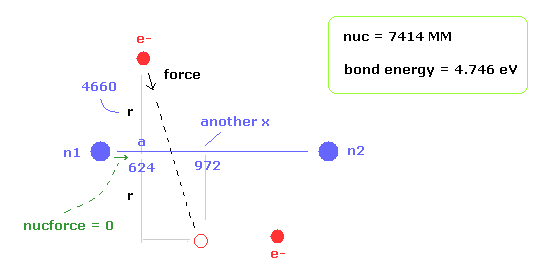
この地点において、1軌道に含まれる ドブロイ波の数 (= Eq.2 ) は0.977 になる。
この値は だいたい 1 になるが 若干異なる。
なぜなら電子軌道は x 方向に少し揺れるからである。
もう1つの x 座標 ( a, r ) = ( 972, 4662 ) のとき、このドブロイ波は 1.009 になる。
結果的に 平均のドブロイ波は ( 0.977 + 1.009 ) / 2 = 0.993 となる。
この値は "1" に近くなる。
| nuc (MM) | r (MM) | a (MM) | Energy (eV) | another x | nucforce | aver waves | elefx | after elefx |
|---|---|---|---|---|---|---|---|---|
| 6000 | 4875.1 | 1662 | 3.699 | 1858 | 0.00 | 0.9933 | +0.024 | +0.013 |
| 6500 | 4744.3 | 1059 | 4.408 | 1351 | 0.00 | 0.9933 | +0.039 | +0.005 |
| 7000 | 4684 | 775 | 4.689 | 1107 | 0.00 | 0.9933 | +0.046 | -0.006 |
| 7200 | 4671 | 697 | 4.732 | 1037 | 0.00 | 0.9933 | +0.047 | -0.011 |
| 7414 | 4662.3 | 629 | 4.746 | 972 | 0.00 | 0.9933 | +0.048 | -0.014 |
| 7600 | 4658 | 577 | 4.738 | 922 | 0.00 | 0.9933 | +0.048 | -0.017 |
| 8000 | 4657 | 488 | 4.671 | 831 | 0.00 | 0.9933 | +0.048 | -0.023 |
ここでは 新しい単位 1 MM = 1 × 10
Table 1 に示すように、共通な条件 nucforce = 0 と ドブロイ波 = 0.9933 を選ぶとき、核間距離 nuc = 7414 MM (= 実験値 ) のときの 結合エネルギーが 最も大きくなる。
すでに述べたように、安定な原子核と ドブロイ波長を考慮すると、水素原子の 最も安定な状態が決定する。
| nuc (MM) | r (MM) | a (MM) | Energy (eV) | elefx | elefy | nucforce | waves |
|---|---|---|---|---|---|---|---|
| 7414 | 4665 | 890 | 4.746 | 0.00 | 1.271 | 0.08 | 1.001 |
電子に作用する力の x 成分がゼロのとき ( elefx = 0.00 )、ドブロイ波は ちょうど 1.001 になる。
nuc = 7414、 r = 4665、 a = 890 ( これは Table 1 の 629 と 972 の間である ) を代入してみるといい。
(Fig.12) 2つの H 原子が 完全に分離されている。
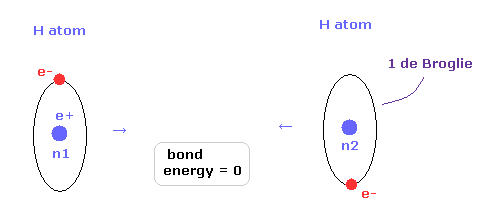
次に 核間距離が nuc = 7414 MM (= 実験値 ) のとき どうして H2 分子が最も安定になるのかという理由について考える。
Fig.12 では、2つの水素原子は 完全に分離しているため、結合エネルギーは ちょうどゼロである。
(Fig.13) 最も安定な H2 の形。
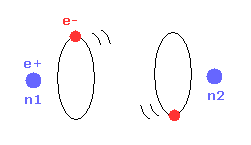
2つの原子核が互いに近づくにつれて、各電子は 2つの正の原子核と相互作用することができる。
そのため 結合エネルギーが大きくなり 安定な H2 分子が形成される。
(Fig.14) 2電子間の反発力。

しかし 2つの電子が 実験値 7414 MM よりもさらに近づくと、2つの電子間の反発力が さらに強くなる。
結果的に "実質的"な中心電荷が小さくなる。
そのため 共通のドブロイ波の条件のもとで、半径 "r" は 大きくなり、結合エネルギーは 実験値よりも小さくなる ( Table 1 参照のこと )。
(Fig.15) 核間距離が短くなると・・
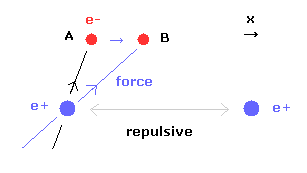
核間距離が短くなると、原子核間の反発力が強くなる。
この反発力をキャンセルするために、2つの電子は 中心方向に移動する必要がある。
Fig.15 に示すように、電子1が x 方向に動くと ( A → B )、電子1による x 方向の引力が強くなる。
しかし この場合 Fig.14 に示すように 2つの電子間の反発力が強くなる。
(Fig.16) 核間距離が短くなる → 不安定な電子。
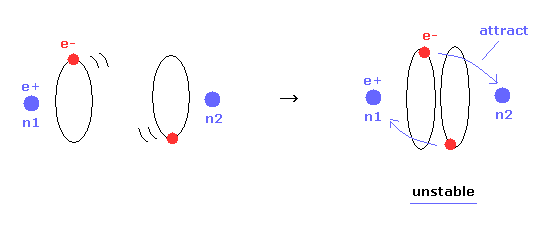
Table 1 では、安定な原子核 ( nucforce = 0 ) の条件を選んだ。
もちろん、分子構造が安定のとき、原子核と電子の両方が安定になる必要がある。
Table 1 に示すように、核間距離が 実験値 (= 7414 MM ) よりも短くなると、電子軌道は不安定になる。
なぜなら その時 "a" と "another-x" の位置にある電子に作用する力が 必ず 正になるからである ( elefx > 0, after-elefx > 0 )。
( つまり この不安定な電子軌道は 別の原子核 n2 に必ず引きつけられていることになる。 Fig.17 右も参照のこと。)
電子軌道が ある場所あたりで安定であるとき、電子は U ターンする必要がある。
この場合は elefx は 正で after-elefx は 負の数になる必要がある ( Fig.17 左 参照 )
(Fig.17) 核間距離が短くなる → 不安定な電子。
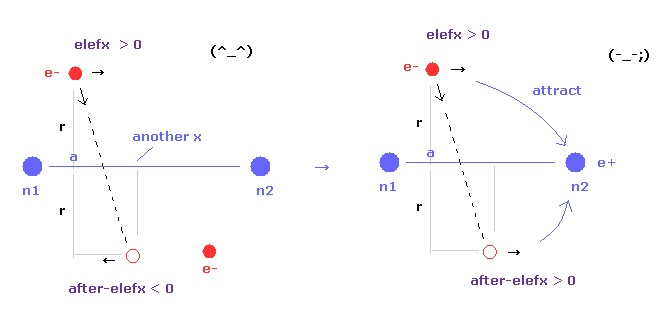
核間距離が短くなるにつれて、電子の x 座標 "a" は 原子核を安定にするために大きくなる。
そのため n1 原子核による 電子1への影響力は弱くなり、n2 の影響力が強くなる。
結果的に 電子軌道は 別の原子核のほうに 引きつけられ 不安定になる。
この電子の不安定性は 核間距離 0.7414 × 10-10 m (= 実験値 ) が最も安定である理由の1つである。
(Fig.18) 安定な軌道は 揺れて かつ U ターンする。

次に ボーア軌道を用いて メタン (CH4) の 本当の姿を調べてみることにする。
(Fig.19) CH4 における 横方向のでっぱり。
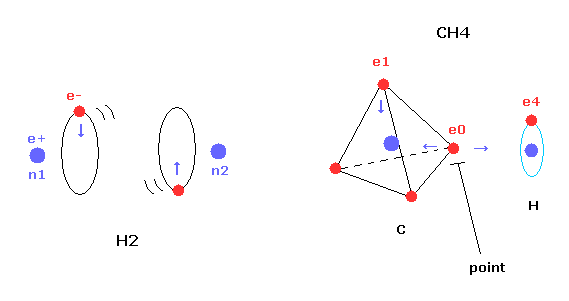
上のセクションでは ボーア軌道を用いて 水素分子 (H2) を表すのに成功した。
また 核間距離が実験値 (= 7414 MM ) のとき、H2 の結合エネルギーが最大になることを示した。
ここでは 新しい単位 1 MM = 1 × 10-14 meter を用いた。
しかし 単純な水素分子と異なり、メタン (CH4) の炭素原子は 4つの 正四面体状に分布した価電子を持つ。
そのため 炭素の1つの電子を 水素の電子軌道と平行になるようにしても、4つの中の別の電子が 必ず水素原子のほうに 突き出てしまう。
この突き出た炭素の電子は 水素原子の原子核を強く引きつけて そのポテンシャルエネルギーを低くする。
また この突き出た電子は 分子構造の不安定性を決定する際の重要な鍵となることを 後で示す。
(Fig.20) コンピュータープログラムの CH4 の構造。
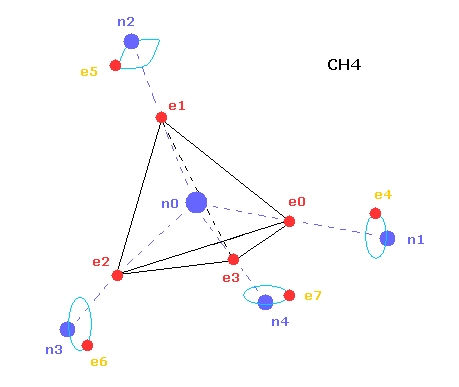
ここで CH4 の本当の性質を調べるために 次の JAVA プログラムを使用する。
メタン分子 (CH4) の サンプル JAVA プログラム。
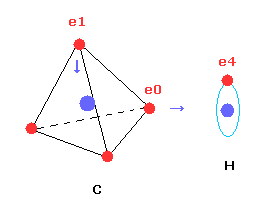
上記のコンピュータープログラムでは、Fig.20 のメタン模型を用いた。
炭素原子の4つの価電子 ( e0, e1, e2, e3 ) が 正四面体状に分布している。
また 4つの水素原子の原子核も正四面体状に分布している。
Fig.20 に示したように、 炭素の電子 e0 と 水素の n1 原子核は 同じベクトル上にある。
( 同様に e1-n2、 e2-n3、 e3-n4 も それぞれ同一のベクトル上にある。 )
(Fig.21) CH4 (= x-z 平面 ) の断面。
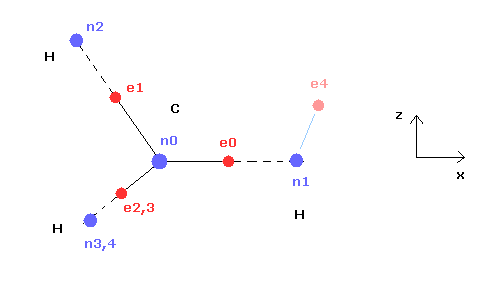
Fig.21 は Fig.20 の断面 ( x- z 平面 ) である。
上記のプログラムでは、テキストボックス上の 電子 e0 と e4 の座標のみ変更できる。
( e0 の x 座標と、 e4 の x、 z 座標のみ変更できる。)
テキストボックス上の e0 と e4 の入力座標に基づいて 残りの炭素の電子 ( e1-e3 ) と 水素の電子 ( e5-e7 ) が 自動的に正四面体状に配置される。
つまり 電子 1、2、3 ( と H の原子核 n2、3、4 ) の x 座標は 必ず同じになっている。
( このプログラムは 画面のスペースの都合上 テキストボックスだけで 絵は示していない。)
(Fig.22) プログラム実行直後の画面。
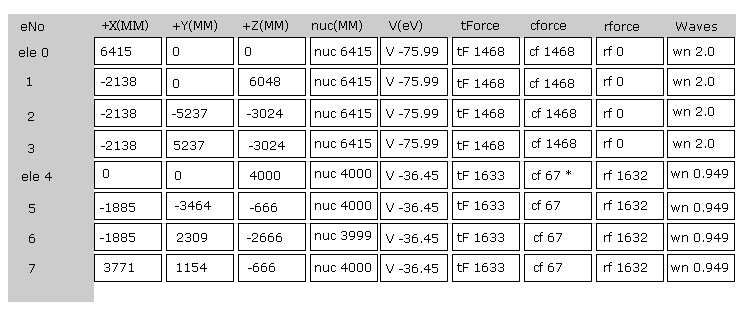
Fig.22 は JAVA プログラムを実行直後の 画面上の表示の上部分である。
ele 0, 1, 2, 3 は 炭素原子に属する電子である。
+X(MM), +Y(MM), +Z(MM) は 各電子の それが属する原子核に対する 相対的な座標である。
( ele 0-3 は 炭素の原子核 n0、 ele4 は H の原子核 n1、 ele5 は n2、 ele6 は n3、 ele7 は n4 に属する。 )
"nuc" は 各電子と それが属する原子核間の距離である。
ここでは 新しい単位 1 MM = 1 × 10-14 meter が使用されている。
"V(eV)" 各電子の位置エネルギーである。
"tForce" は 各電子に作用する トータルな力である。
"cforce" は 各電子に作用する力の 中心 (= C 原子核 ) 方向の力である。
"rforce" は 各電子 ( e4-e7 ) に作用する力の 各 C - H 原子核ライン方向 (= 垂直な ) への力の成分である。
"Waves" は 1軌道に含まれるドブロイ波の数である。
(Fig.23) Force = 1000.
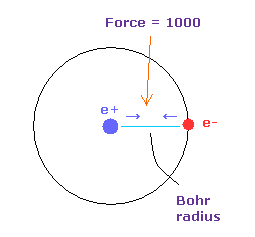
Fig.22 においては 水素原子の基底状態における 電子と原子核間に働く力の強さを "1000" としている。
そのため 電子と +e の原子核間の距離が ボーア半径のとき、その力が 1000 になる。
例えば、力 1468 は 水素原子の基底状態のときの力の 1.468 倍である。
各運動エネルギー (T) から 各ドブロイ波長を計算する。
ここでは ビリアル定理 ( -1/2V = T ) を使用している。
( "V" は ポテンシャルエネルギーである。 )
原子 (= 単一原子核 ) や H2 分子などの場合は それらの計算はシンプルである。
しかし 分子が 2つ以上で かつ 非対称的な 多電子を持つときは、少し注意する必要がある。
各運動エネルギーから 各電子の速度 (= v ) と ドブロイ波長 (= h/mv ) を得ることができる。
(Eq.4) トータルの力 F = 遠心力。
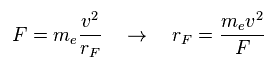
プログラムでは、各電子に作用する力の x、y、z 成分を計算する。
( rhp[el][0, 1, 2] = 力の x、 y、 z 成分。 )
ここでは それら力 F が ある種の遠心力として扱う。
Eq.4 の関係式から ( 近似的な ) 回転半径 (= rF ) を得ることできる。
(Eq.5) 1軌道のドブロイ波。
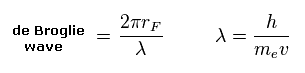
ドブロイの関係式 ( λ = h/mv ) を用いて、1軌道 (= 2πrF ) に含まれるドブロイ波の数を計算する。
炭素の外殻電子 e0-e3 のドブロイ波は "2"、水素の電子 e4-e7 のドブロイ波は "1" に近くなるべきである。
(Fig.24) メタンの C-H 結合。
メタンの 4つすべての C-H 結合を分離するのに必要なエネルギーは 1663 kJ/mol ( = 17.235 eV ) である。
つまり メタンの基底状態のエネルギーは (= 4つの炭素の価電子 + 4つの水素原子 ) は、 -148.024 -54.416 -17.235 = -219.675 eV となる。
( ここでは 炭素の4つの価電子ののエネルギーを -148.024 eV = 1-4 イオン化エネルギーの合計とした。)
平均の C-H 結合長は 1.09 × 10-10 meter (=10900 MM ) である。
(Fig.25) C-H 結合のドブロイ波。

Fig.25A の e0 では、上のド・ブロイ波の計算方法を そのまま使うことはできない。
酸素 (O) の電子 0 (e0) では、水素原子核からの反対方向の引力 (fx) のため、Fig.25A に示すように 力 F0 は、電子1の力 F1 よりも弱くなる。
つまり、Eq.4 では、e0 の”仮の”半径 r1 は e1 に比べて長く なる。
これは、Eq.1, Eq.2 の計算方法を使うと、e1 (< 2.0) よりもより多くのド・ブロイ波 (> 2.0) が e0 軌道に含まれてしまう。
しかし、もし、1つのみの電子軌道に注目すると (Fig.25B)、ド・ブロイ波の数 ( = 2.0 ) はその軌道の位置や形を変化させることで維持される。
(正の電荷の水素原子核は、この電子軌道を少し平行移動させ、またそれを楕円形に変化させる。)
つまり、C-H 結合の炭素の電子の 1軌道のドブロイ波を計算するとき、近似的に 炭素内のみにおける力とエネルギーを考慮することにする。
(Fig.26) C-H 結合における各力。
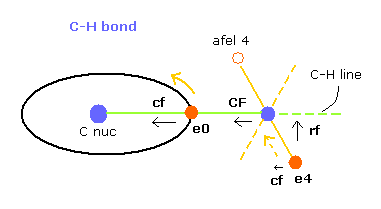
このプログラムでは "cf" は 各電子に作用する力の C 原子核方向への成分である。
"rf" は 電子 4-7 に作用する力の 各 C-H ライン方向に向かう成分である。
"afel 4" は 力の方向へ移動した後の 電子の位置の意味である。
( つまり 各電子は この場所のあたりを横方向に振動している。 )
電子軌道が ある地点で安定になるためには、この e4 の "cf" は 正になり afel 4 の "cf" は 負になる必要がある。
そして それらの絶対値は 安定のためには ほぼ同じにならなければならない。
( これは 安定な分子結合における 重要な点の1つである。)
"CF" は 各水素原子核に作用する力の C 原子核方向への力である。
つまり これら CF と cf が 正の値のとき、これらの粒子は C 原子核方向へ引きつけられていることになる。
(Fig.27) "afel 4" の位置。

"afel 4" の x 座標を計算するとき、 "cf" の "rf" に対する力の比を用いる。
また afel 4 の z (と y ) 座標は 元の e4 に等しいとしてある。
(Fig.28) 平均の位置?

Fig.28 の分布を用いて 各粒子の力とドブロイ波を計算しようとするとき、4つの外殻電子と水素原子核が 平均的な値以上に 互いに強く引きつけられる。
炭素の外殻電子軌道の半径は 約 6400 MM であり、これは 水素原子のボーア半径 5292 MM とほぼ同じである。
しかし 炭素の外殻電子軌道は 2ドブロイ波長であり、これは 水素原子の電子の 約 2倍の速さである。
そのため 水素原子との相互作用を考慮するとき、炭素原子に関して平均の分布を考える必要がある。
(Fig.29) 炭素原子の外殻電子の平均分布。
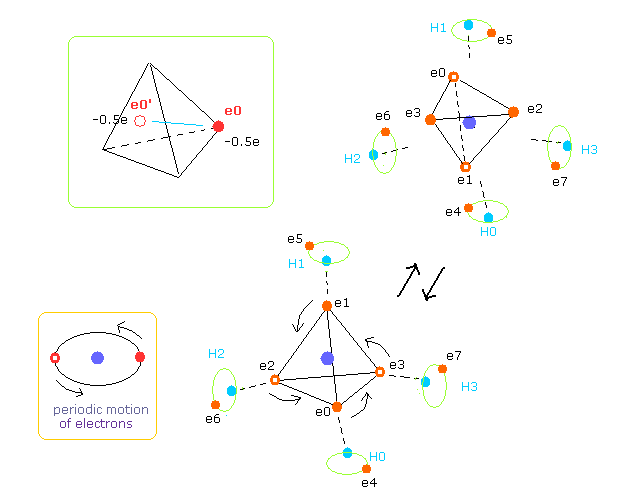
Fig.29 に示すように、炭素の 4つの外殻電子は ほぼ楕円軌道である。
そのため 各電子の逆方向の位置が 平均値をとる際に重要になる。
実際に ビリアル定理は 無限の時間周期に関する 平均値に等しい。
そのため 速いスピードで動いている 炭素の4つの外殻電子は 半分の電荷を持つ 8つの電子を考えることができる ( -1.0e → -0.5e, -0.5e × 8 = -4e )。
( もちろん、電子 0-3 同士の反発力を計算するときは 元の4つの価電子のままで計算しないと、値が高くなりすぎてしまうので注意。)
ここでは C-H 結合長として 実験値 (= 10900 MM ) を選んだ結果を示す。
下に示す座標 ( ele 0 と ele 4 の "←" の値 ) を プログラム実行後、各テキストボックスに入力して"enter" キーを押すように。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 ← | 0 | 0 | nuc 6415 | V -76.45 | cf 1432 | rf 0 | wn 2.0 |
| ele 4 | 520 ← | 0 | 4060 ← | nuc 4093 | V -35.03 | cf 278 | rf 1568 | wn 0.917 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -75.17 | cf 1488 | rf 0 | wn 2.0 |
| afel 4 | -922 | 0 | 4060 | nuc 4163 | V -36.28 | cf -264 | rf 1396 | wn 1.083 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -445.95 eV | wave 2.0 | wave 1.0 |
Table 1 は C-H 結合長が 実験値 (= 10900 MM ) のときの結果である。
平均のドブロイ波は 電子 0 で "2.0"、 電子 4 で "1.0" である。
また H0 原子核をストップさせる ( force CF = 0、 Fig.26 も参照のこと )。
この条件のもとで、全ポテンシャルエネルギーは -445.95 eV で これは 実験値 -219.675 × 2 = -439.35 eV とほぼ等しい。
( この少しの差は 後で説明するが、電子分布の違いによるものである。)
重要な点は C-H 結合長が 10900 MM のとき、電子 4 の軌道も 安定になるということである。
なぜなら ele 4 に作用する力の横方向成分 ( cf = 278 ) は afel 4 のもの ( cf = -264 ) と正反対でほぼ等しい大きさだからである。
(Fig.30) メタンでは 電子と原子核の両方が安定になる。
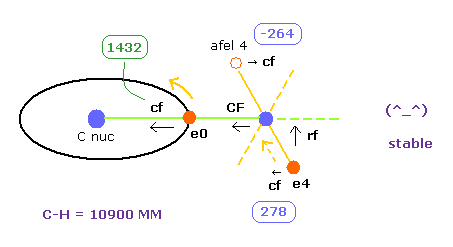
この電子の安定性は Fig.16、Fig.17、fig.18 の水素分子 (H2) のケースに 似ている ( Table 1 参照のこと )。
水素分子においても after-elefx は elefx と 逆の符号であり、電子が ある場所で 横方向に安定的に振動している。
(Fig.17) H2 分子の安定した電子運動 = 左図。

(Fig.18) 安定した軌道は 振動しており かつ U ターンする。

次に C-H 結合長 = 9500 MM (= 0.950 × 10-10 meter ), を選び C-H ボタンをクリックする。
そして CF=0 ( 原子核の安定 )、平均のドブロイ波 2.0 (ele0) と 1.0 (ele4) の値を目指す。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -79.06 | cf 232 | rf 0 | wn 2.0 |
| ele 4 | 927 | 0 | 3129 | nuc 3263 | V -44.05 | cf 782 | rf 2341 | wn 0.834 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -76.33 | cf 353 | rf 0 | wn 2.0 |
| afel 4 | -1165 | 0 | 3129 | nuc 3338 | V -46.45 | cf -715 | rf 1771 | wn 1.167 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -492.47 eV | wave 2.0 | wave 1.0 |
(Fig.31) "e4" は C に引きつけられ、 "e0" は H に引きつけられる。
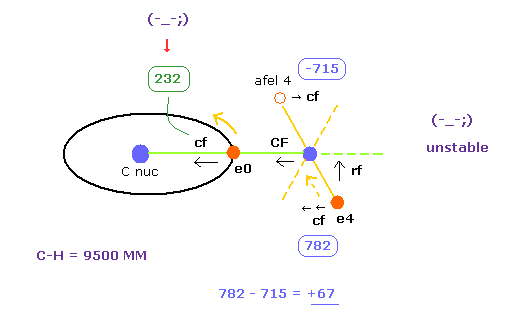
Table 4 に示すように C-H 結合長が 実験値 (= 10900 MM ) よりも 少し 短くなると (= 9500 MM )、 電子の安定性が 壊れてしまう。
最初に 炭素原子核に属する 電子0 が H の原子核に引きつけられすぎる。
なぜなら e の "cf" は Table 3 の (= 1432 ) よりも かなり小さい (= 232 ) からである。
(Fig.23) Force = 1000.

Fig.23 で述べたように、 H 原子の 電子と原子核の間の力を"1000" と定義した。
つまり 電子 と +e の原子核の距離が ボーア半径のとき、その力は 1000 になる。
"232" は 炭素の電子が 炭素原子核周囲を安定的に運動するには 小さすぎる。
(Fig.31') 水素原子が炭素に近づきすぎ → メタンは不安定。
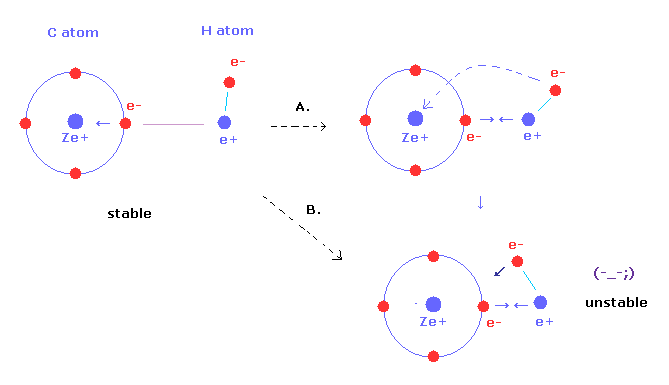
2つ目に、C-H 結合長が短くなると、H の原子核は 炭素の電子0 に より引きつけられる。
この引力をキャンセルするには、H 原子の 電子4 は 横方向に よりワイドに揺れる必要がでてくる (= Fig.31'A ) 。
しかし 一方で 電子4 に対する 炭素原子核の引力も強くなる (= Fig.31'B )。
Fig.31'A のように 炭素の引力が強くなった影響下で H の電子軌道が 横に倒れすぎることは 不自然である。
なぜなら 電子4 の軌道が H の原子核をストップするための軌道状態を保てないからである。
( Table 4 (Fig.31) の "cf" の違い +67 は Table 3 の +14 よりも 大きい。 )
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -80.89 | cf -757 | rf 0 | wn 2.0 |
| ele 4 | 1064 | 0 | 2676 | nuc 2879 | V -50.13 | cf 1230 | rf 2892 | wn 0.795 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -77.11 | cf 588 | rf 0 | wn 2.0 |
| afel 4 | -1212 | 0 | 2676 | nuc 2937 | V -52.95 | cf -1156 | rf 1934 | wn 1.204 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -524.11 eV | wave 2.0 | wave 1.0 |
(Fig.32) e0 は H に引かれ、 e4 軌道は横に倒れる。
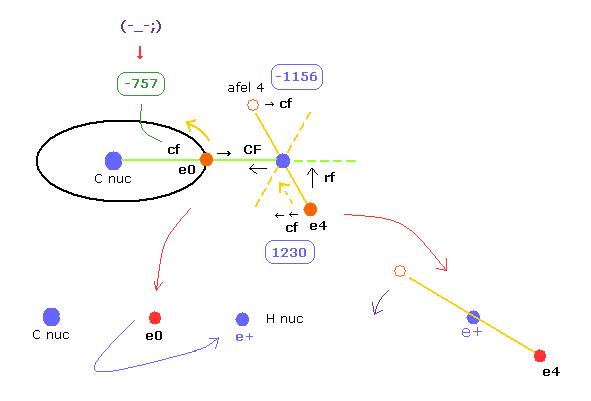
C-H 結合長が さらに短く (= 9000 MM ) なると、 炭素の 電子 0 は 炭素原子核のかわりに H の原子核に引き寄せられる。
つまり 炭素の構造が壊れてしまうことになる。
また e4 の軌道が 横方向に倒れすぎて、e4 の運動を 不安定にする。
"cf" の違い 1230 - 1156 = 74 は 上のよりも広くなる。
(Fig.32') C-H の長さが短くなると...

結果的に C-H 結合長が 実験値よりも短くなると、電子もしくは原子核の運動の1つが 不安定になる。
つまり 分子結合においては 電子と原子核の両方の安定性を考慮する必要がある。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -75.47 | cf 1797 | rf 0 | wn 2.0 |
| ele 4 | 273 | 0 | 4494 | nuc 4502 | V -31.91 | cf 141 | rf 1320 | wn 0.956 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -74.77 | cf 1829 | rf 0 | wn 2.0 |
| afel 4 | -690 | 0 | 4494 | nuc 4546 | V -32.6 | cf -142 | rf 1248 | wn 1.044 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -429.59 eV | wave 2.0 | wave 1.0 |
C-H 結合長が 実験値より長くなると、ポテンシャルエネルギーは
( Table 3 の -445.95 eV と Table 6 の 429.59 eV を比較するように。 )
つまり 結合エネルギーと安定性のつりあいのとれた地点が メタン (CH4) の構造を決定することになる。
もちろん、これらの過程では クーロン力と ドブロイ波 ( 2.0 と 1.0 ) の 2つの性質が 決定的な役割を果たしている。
(Fig.33) もし 炭素の4つの価電子が もっと広く分布していると・。
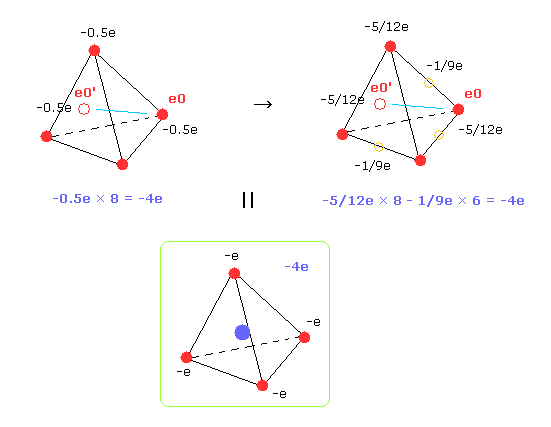
上のセクションでは 水素原子の平均の軌道を得るとき、炭素の4つの外殻電子が 半電荷の8つの電子として C 原子核周囲に分布していると仮定した。
実際に 炭素の外殻電子は 水素の電子よりも 速い速度で運動している。
また 1つの電子が去った後にも すぐに別の電子が 水素のもとにやってくる。
それらの回転周期も異なっているわけである。
しかし Table 3 に示したように、全ポテンシャルエネルギーの計算結果 (= -445.95 eV ) は 実験値 (= -439.35 eV ) と少し異なる。
そのため 炭素の4つの価電子が 炭素原子核の周囲により広く分布していると仮定する。
Fig.33 右では -5/12e の電荷をもつ 8つの電子と -1/9e の電荷をもつ 6つの電子 ( 正四面体の 6 つの辺の中点上 ) を仮定した。
もちろん それらの全電荷は -4e のままである。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -76.02 | cf 1403 | rf 0 | wn 2.0 |
| ele 4 | 405 | 0 | 4308 | nuc 4326 | V -33.07 | cf 219 | rf 1427 | wn 0.928 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -74.91 | cf 1431 | rf 0 | wn 2.0 |
| afel 4 | -918 | 0 | 4308 | nuc 4404 | V -34.2 | cf -199 | rf 1299 | wn 1.072 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -436.41 eV | wave 2.0 | wave 1.0 |
この CH4 の電子の分布は ほぼ実験値 (= -439.35 eV ) を示す。
また Table 3 のように、ele4 と afel 4 の cf の値は適切なもの ( 219 と -199 ) である。
これらの値は 符号が逆で、それらの絶対値の値が ほぼ同じ ( 219 - 199 = 20 ) である。
これはつまり 電子 4 の軌道は この模型では 安定になる。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -78.22 | cf 158 | rf 0 | wn 2.0 |
| ele 4 | 864 | 0 | 3415 | nuc 3522 | V -40.6 | cf 633 | rf 2064 | wn 0.844 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -75.84 | cf 1431 | rf 0 | wn 2.0 |
| afel 4 | -1232 | 0 | 3415 | nuc 3630 | V -43.08 | cf -499 | rf 1649 | wn 1.156 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -475.32 eV | wave 2.0 | wave 1.0 |
C-H の長さが 実験値よりも短くなると ele0 の運動が不安定になる。
なぜなら Table 4 と Fig.31 のように、 電子 0 に対する 炭素のクーロン引力は 非常に 弱い ( cf = 158、で これを Table 7 の 1403 と比較するように )。
一方で ele4 の軌道は C の原子核に より引かれる。
( cf 633 - 499 = 134 となる。 これを Table 7 の 219 -199 = 20 と比較するように。 )
結果的に 両方の電子の運動は C-H の距離が 9500 MM (= 0.950 × 10-10 meter ) のときに不安定になる。
(Fig.33') 水素が炭素に近くなりすぎる → メタンが不安定。

| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 6415 | 0 | 0 | nuc 6415 | V -79.7 | cf -851 | rf 0 | wn 2.0 |
| ele 4 | 1064 | 0 | 2932 | nuc 3103 | V -46.29 | cf 1005 | rf 2573 | wn 0.803 |
| afel 0 | 6415 | 0 | 0 | nuc 6415 | V -76.58 | cf -891 | rf 0 | wn 2.0 |
| afel 4 | -1274 | 0 | 2932 | nuc 3197 | V -49.37 | cf -786 | rf 1883 | wn 1.197 |
| H0 nuc | total V | averwave-0 | averwave-4 |
|---|---|---|---|
| force= 0 | -503.98 eV | wave 2.0 | wave 1.0 |
さらに C-H の結合長が短くなると、電子0 が C でなく H の原子核に引きつけられるようになってしまう ( cf -851 ).
これはつまり C-H の長さが 9000 MM のとき、メタンの炭素構造が壊れてしまうことを意味している。
一方で 電子 4 の軌道は C の原子核により引きつけられる ( cd 1005 - 786 = 219 ).
つまり 両方の電子軌道が この場合は 不安定になる。
結果的に メタンの核間距離が 10900 MM のときに、その構造が最も安定になる。
(Fig.34) C-H 結合長が短くなると・・

ここでは C-H 結合長が H 原子核の安定性にどう影響するか 簡潔に述べるとする。
(Fig.A-1) H 原子核に対する反発力。
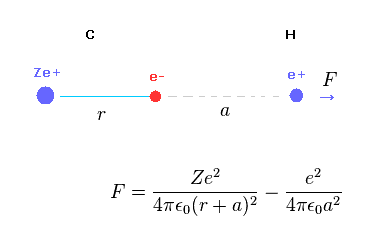
Fig.A-1 は 水素原子核に対する (反発)力 F を示している。
C 原子核 Ze+ は 反発力として作用して、 C の電子は 水素原子核に対する引力として作用する。
(Fig.A-2) 距離 "a" が長いとき。

C の電子と H 原子核の距離 "a" が "r" よりも かなり長いとき、"r+a" と "a" の距離の差は小さくなる。
このケースでは、Fig.A-1 における 炭素の全電荷は +(Z-1)e に近くなる。
そのため 水素原子核は C 原子核によって反発されることになる。
(Fig.A-3) 距離 "a" が短くなると・・。
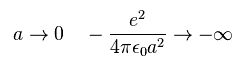
しかし C 電子と H 原子核の距離が非常に短くなると、C 電子による引力は クーロンの逆二乗の法則のため 強くなる。
結果的に C-H 結合長が非常に短くなると H 原子核が その安定位置を保てなくなる。
( また H の電子も安定位置を保てない。)
これが C-H 結合長が 1.090 × 10-10 m で保たれている主要な要因と考えられる。
水 (H2O) は 私達の生命を維持するのに 必要不可欠な物質である。
しかし今でさえ 従来の量子力学的な手法を用いても 水に関する重要な性質については あまりよく分かっていないのである。
例えば 水が 氷になると どうして その密度が再び低くなるのか 原子、電子レベルにおいて よく分かっていないのである。
これら謎の多い水に関する重要な性質を 具体的なボーア軌道などを用いて調べることは非常に興味深いことと思われる。
(Fig.35) 推定される 水分子 (H2O) 模型。
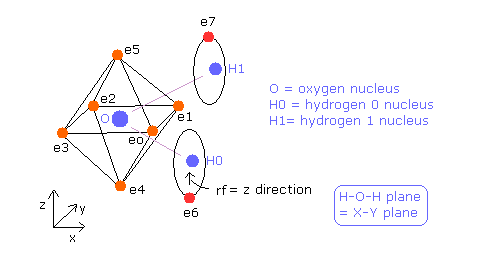
ここでは 水の構造を調べるのに 下の サンプル JAVA プログラムを使用する。
水分子 (H2O) を調べる サンプル JAVA プログラム。
このプログラムでは +X(MM), +Y(MM), +Z(MM) は、各電子が属する原子核に対する 相対的な位置を表している。
電子 0-5 は 価電子として 酸素原子に属しており、電子6 は H0 原子核、電子7 は H1 原子核に属している。
基本的に O 原子核、H0 原子核、H1 原子核、電子0-3 は 同じ x-y 平面上にあるとする。
また、 e0-e1、 e2-e3、 e4-e5、e6-e7 は それぞれペアを形成しているため、 テキストボックス上の ele 0、 ele 2、 ele 4、 ele 6 の座標のみ変更できる。
これらの入力値に基づいて 残りの座標が自動的に決まる。
他の方法は メタンの場合とほぼ同じである ( このページも参照のこと )。
(Fig.36) 水 (H2O) の分子構造。
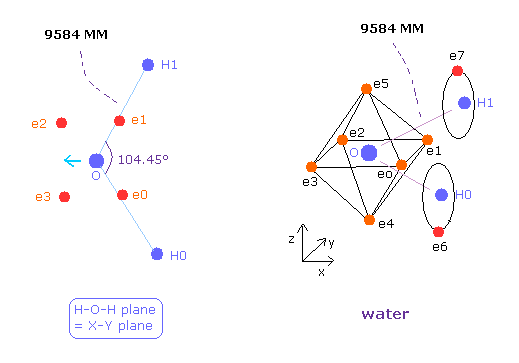
水分子の 単一の O-H 結合エネルギーは、 9.6066 eV (=926.9 kJ/mol) / 2 = 4.8033 eV である。
そのため H2O の全エネルギー は -433.103 (O) - 2 × 13.606 (H) - 9.6066 (結合エネルギー) = -469.92 eV.
ここで 433.103 eV は 酸素の 6つ の価電子の全イオン価エネルギーである。
そして 13.606 eV は 水素原子の基底状態のイオン化エネルギーである。
H2O の O-H 結合長は 9584 MM (= 0.9584 × 10-10 meter) である。
H-O-H の角度は 104.45 度であり、これは 90 度より少し大きい。
炭素の正四面体構造と異なり、酸素の 6つの価電子は 原子核を挟んで すでに対称的な位置に配置されており、
( 例えば e0-e2, e1-e3.. )、 また その回転半径は炭素よりも小さい。
そのため この H2O 構造をそのまま用いるとする。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 3130 | -3366 | 0 | nuc 4596 | V -147.33 | cf 5459 | rf 0 | wn 1.983 |
| ele 1 | 3130 | 3366 | 0 | nuc 4596 | V -147.33 | cf 5459 | rf 0 | wn 1.983 |
| ele 2 | -3250 | 3250 | 0 | nuc 4596 | V -145.05 | cf 6184 | rf 0 | wn 2.018 |
| ele 3 | -3250 | -3250 | 0 | nuc 4596 | V -145.05 | cf 6184 | rf 0 | wn 2.018 |
| ele 4 | 331 | 0 | -4585 | nuc 4596 | V -144.5 | cf 6218 | rf 0 | wn 1.999 |
| ele 5 | 331 | 0 | 4585 | nuc 4596 | V -144.5 | cf 6218 | rf 0 | wn 1.999 |
| ele 6 | 350 | -580 | -4340 | nuc 4392 | V -31.11 | cf 285 | rf 1377 | wn 0.869 |
| ele 7 | 350 | 580 | 4340 | nuc 4392 | V -31.11 | cf 285 | rf 1377 | wn 0.869 |
| aele 6 | -752 | 842 | -4340 | nuc 4484 | V -34.14 | cf -228 | rf 1221 | wn 1.131 |
| O nuc FX,FY,FZ | H0 nuc On, Hn | total V | averwave-0 | averwave-6 |
|---|---|---|---|---|
| force = 0, 0, 0 | force = 1, 16 | -936.02 eV | wave 2.00 | wave 1.00 |
ビリアル定理によれば、全ポテンシャルエネルギー V は 全エネルギー E の 2倍である。
( トータル V = = -469.92 × 2 = -939.84 eV. )
そのため Table 10 の計算結果は いい。
また 水素の電子 (= ele 6 ) の運動 は ほぼ安定している ( cf = 285 and a-cf = -228 )。
この "cf" は電子に作用する力の O 原子核方向への力である。
Table 10 では、O と H 原子核に対する トータルの力が ほぼゼロで、平均のドブロイ波が 約 2.0 ( e0-5 )、 1.0 ( e6 ) の条件に近くなるのを目指している。
また CH4 のケースのように e0-5 の平均のドブロイ波を求めるのに、酸素原子内のみで 各ポテンシャルエネルギーと力を計算した。
(Fig.37) H2O における 電子分布の変化。

Fig.37 に示したように、 もし H-O-H の角度 (= 104.45° ) が 正八面体の 90°よりも 大きいと、 e0 と e1 は 水素原子核に引きつけられて 外方向へ移動する。
結果的に e0 - O - e1 角は 90°よりも広くなる。
この構造変化に続いて、 e4 - O -e5 角は もとの 180°よりも小さくなる。
結果的に 水素原子核による反発力は これらの構造変化によってキャンセルされる。
( e4 と e5 は O 原子核を H 原子の方向へ引っ張る。)
Table 1 では、 O 原子核と 6つの価電子の距離を固定している ( nuc = 4596 MM )。
また ele 4 と ele 5 の座標を固定して、 ele 0 ( ele 1 ) と ele 4 ( ele 5 ) のみを動かした。
この条件では、e0 - O - e1 の角度が 94°、 e4 - O - e5 の角度が 171°のとき、そのポテンシャルエネルギーが 最も低くなり (= -936.02 eV )、それは 実験値 -939.84 eV にほぼ近い値である。
(Fig.37') H-O-H の角度が 90°のとき、電子の構造変化がブロックされる。

一方で、H-O-H 角が 90°のとき、 電子 e0 と e1 は 外方向へ移動できないため、 e4 と e5 も 動くことができない。
なぜなら O-e0 と O-el の線は 最初から O-H0 と O-H1 の線上にあるからである。
そのため H 原子核による反発力をキャンセルするための構造変化が起こらないことになる。
さらに H 原子核による反発力が 104.45°のときに比べて 90°のときは 角度が急になった分 強くなる。
そのため 水分子の H-O-H の角度は 強くなる反発力と 構造変化のブロックのため 90°になれないことになる。
( H-O-H の角度 104.45 のからくりは この 構造変化にあると言っていい。 )
(Fig.37'') 四フッ化硫黄 ( SF4 ).
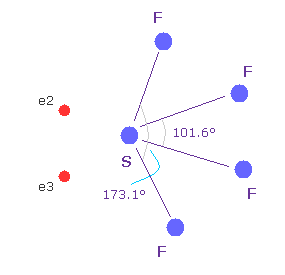
似たような構造変化は 四フッ化硫黄 (= SF4 ) で見られる。
硫黄 (= S ) は 酸素原子のように 6つの価電子を持つ。
フッ素の強い電気陰性度のために、硫黄の電子は フッ素側に引きつけられ、そのサイドの電子密度が弱くなり、これが 構造変化を引き起こす。
このメカニズムは 上記の H2O と少し異なる。しかし その構造変化は似ている。
( フッ素と水素の重要な違いは F は 7つもの価電子のため 他の原子核の価電子が多くなるにつれて それらをを反発するが、H は 引きつけられるということである。)
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 3000 | -3483 | 0 | nuc 4596 | V -147.25 | cf 5456 | rf 0 | wn 1.984 |
| ele 1 | 3000 | 3483 | 0 | nuc 4596 | V -147.25 | cf 5456 | rf 0 | wn 1.984 |
| ele 2 | -3250 | 3250 | 0 | nuc 4596 | V -145.05 | cf 6182 | rf 0 | wn 2.016 |
| ele 3 | -3250 | -3250 | 0 | nuc 4596 | V -145.05 | cf 6182 | rf 0 | wn 2.016 |
| ele 4 | 450 | 0 | -4574 | nuc 4596 | V -144.54 | cf 6223 | rf 0 | wn 1.998 |
| ele 5 | 450 | 0 | 4574 | nuc 4596 | V -144.54 | cf 6223 | rf 0 | wn 1.998 |
| ele 6 | 340 | -597 | -4380 | nuc 4433 | V -30.74 | cf 279 | rf 1351 | wn 0.87 |
| ele 7 | 350 | 580 | 4340 | nuc 4392 | V -31.11 | cf 285 | rf 1377 | wn 0.869 |
| aele 6 | -700 | 888 | -4380 | nuc 4523 | V -33.78 | cf -223 | rf 1203 | wn 1.129 |
| O nuc FX,FY,FZ | H0 nuc On, Hn | total V | averwave-0 | averwave-6 |
|---|---|---|---|---|
| force = 0, 0, 0 | force = 4, 21 | -935.20 eV | wave 2.00 | wave 1.00 |
Table 11 は H-O-H の角度が 実験値 (= 104.45°) より 大きい (= 110° ) ときの結果である。
この条件のとき、角度 e0-O-e1 と e4-O-e5 が それぞれ 98° と 168° のとき、そのポテンシャルエネルギーは 一番低くなる (= -935.2 eV )。
H-O-H の角度が大きくなるにつれて、酸素の価電子が 両方の H 原子核と 相互作用できなくなる。
結果的に、そのポテンシャルエネルギーは高くなるため、H2O の分子は不安定になる。
つまり 104.45°の H-O-H の角度は いわゆる 平衡地点である。
(Fig.38) C-H と O-H 結合の違い。
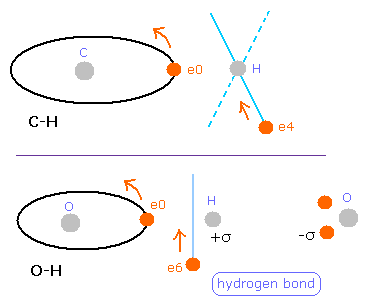
しかし メタンの C-H 結合 (= Table 7 ) と異なり、この水素の電子は 酸素の原子のほうへ少し引きつけられる
( 285 - 228 = 57 )。
( もちろん、これらの絶対値は "200" ほどで これはメタンのケースと同じである。 )
おそらく この O 原子核による 強い引力は 水素結合に関係している。
また 実際に H2O は メタンよりも OH- + H+ に分解しやすい。
H2O は 単独でいるよりも、他の水分子と結合したほうが より安定である。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 3130 | -3366 | 0 | nuc 4596 | V -148.13 | cf 5245 | rf 0 | wn 1.980 |
| ele 1 | 3130 | 3366 | 0 | nuc 4596 | V -148.13 | cf 5245 | rf 0 | wn 1.980 |
| ele 2 | -3250 | 3250 | 0 | nuc 4596 | V -145.19 | cf 6199 | rf 0 | wn 2.021 |
| ele 3 | -3250 | -3250 | 0 | nuc 4596 | V -145.19 | cf 6199 | rf 0 | wn 2.021 |
| ele 4 | 370.5 | 0 | -4582 | nuc 4596 | V -144.6 | cf 6230 | rf 0 | wn 1.999 |
| ele 5 | 370.5 | 0 | 4582 | nuc 4596 | V -144.6 | cf 6230 | rf 0 | wn 1.999 |
| ele 6 | 390 | -750 | -3894 | nuc 3984 | V -34.26 | cf 425 | rf 1639 | wn 0.834 |
| ele 7 | 390 | 750 | 3894 | nuc 4984 | V -34.26 | cf 425 | rf 1639 | wn 0.834 |
| aele 6 | -849 | 849 | -3894 | nuc 4075 | V -38.26 | cf -336 | rf 1389 | wn 1.166 |
| O nuc FX,FY,FZ | H0 nuc On, Hn | total V | averwave-0 | averwave-6 |
|---|---|---|---|---|
| force = 0, 0, 0 | force = 1, 12 | -944.4 eV | wave 2.00 | wave 1.00 |
O-H 結合長が短いとき、O 原子核に対する反発力は 強くなる。
この反発力をキャンセルするために、6つの価電子は H 原子のほうへ移動する必要がある。
O-H 結合が短いとき、酸素の正八面体構造は壊れることになる。
このゆがみは ドブロイ波の数の違いが大きくなることに現れる。
(Fig.39) 酸素の構造が壊れる。
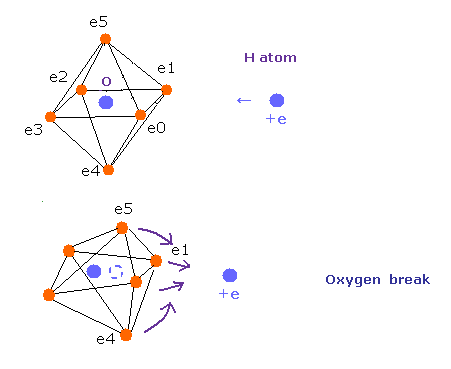
また、H 原子の電子 6 が O 原子核により引きつけられる ( cf 425 - 336 = 89 )。
これらの力の絶対値は より大きくなっている (= 約 "400" )。
そのため H 原子の電子軌道は メタン分子のように 不安定になる。
| eNo | +X (MM) | +Y (MM) | +Z (MM) | nuc | V | cforce | rforce | Waves |
|---|---|---|---|---|---|---|---|---|
| ele 0 | 3000 | -3483 | 0 | nuc 4596 | V -149.02 | cf 4953 | rf 0 | wn 1.978 |
| ele 1 | 3000 | 3483 | 0 | nuc 4596 | V -149.02 | cf 4953 | rf 0 | wn 1.978 |
| ele 2 | -3250 | 3250 | 0 | nuc 4596 | V -145.36 | cf 6199 | rf 0 | wn 2.023 |
| ele 3 | -3250 | -3250 | 0 | nuc 4596 | V -145.36 | cf 6199 | rf 0 | wn 2.023 |
| ele 4 | 527 | 0 | -4566 | nuc 4596 | V -144.78 | cf 6244 | rf 0 | wn 1.997 |
| ele 5 | 527 | 0 | 4566 | nuc 4596 | V -144.78 | cf 6244 | rf 0 | wn 1.997 |
| ele 6 | 570 | -800 | -3423 | nuc 3561 | V -38.38 | cf 637 | rf 1994 | wn 0.800 |
| ele 7 | 570 | 800 | 3423 | nuc 3561 | V -38.38 | cf 637 | rf 1994 | wn 0.800 |
| aele 6 | -771 | 931 | -3423 | nuc 3630 | V -43.38 | cf -546 | rf 1538 | wn 1.201 |
| O nuc FX,FY,FZ | H0 nuc On, Hn | total V | averwave-0 | averwave-6 |
|---|---|---|---|---|
| force = 0, 0, 0 | force = -1, 22 | -955.11 eV | wave 2.00 | wave 1.00 |
O-H 結合がさらに短くなったとき (= 8500 MM )、酸素の構造は H 原子核による反発力をキャンセルするために より壊れる必要がある。
また H 電子の軌道は 不自然に傾く必要がある ( cf 637, -546 )。
ele 0 と ele 4 に作用する力の 差も より大きくなる ( cf は4953 と 6244 )。 Table 10 ( cf 5459 と 6218 ) と比較するように。
これはつまり 6つの電子軌道の周期が 不規則になることを意味する。
(Fig.39') 酸素様原子。
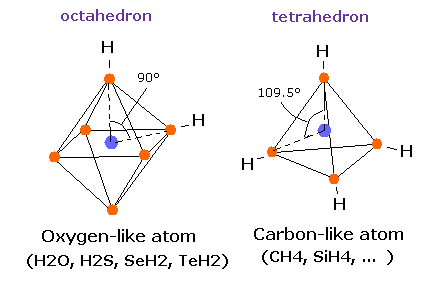
驚くべきことに、他の酸素様原子である、硫黄(S)、セレン(Se)、テルル (Te) においては ( これらは、6つの価電子を持つが )、H-S-H, H-Se-H, H-Te-H の角度は、それぞれ 92.1°、91.0°, 89.5° となり、ほぼ90°になるのである。
つまり、これらの酸素様原子においては、6つの価電子は、ほぼ”正八面体状に”配置されているということができる。
酸素原子においては、水素原子が、他の原子よりも、酸素原子核に より近づいているため、
酸素と水素の原子核間のクーロン反発力によって、酸素原子核を安定に保つために、水分子(H2O) は、”正八面体”の構造を保つことができないと考えられる。
( 例えば、SH2 の 92°のケースでは、反発力は 104.45°の H2O の 3分の1以下になる。)
(Fig.39'') 六フッ化硫黄 SF6 = 正八面体。
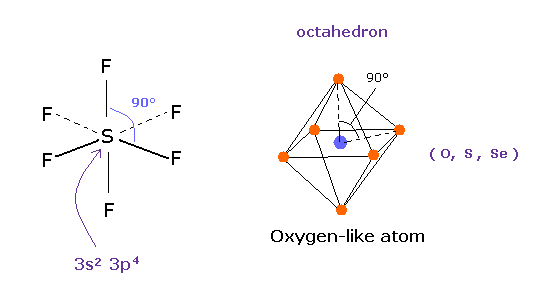
量子力学によれば、硫黄 (S) は 酸素原子のように 6つの価電子をもつ。
( 3s × 2 + 3p × 4 = 6. )
そして 安定な 六フッ化硫黄は ちょうど 正八面体構造を持ち、その F-S-F 角は ちょうど 90°である。
この結果は 明らかに 量子力学が主張する 3s2 3p4 状態が 間違いであり、対称的なクーロン反発力が ここで有効であることを示している。
エタンのすべての結合 ( 6 × C-H + C-C ) を切断するのに、2826.1 kJ/mol (= 29.29 eV) のエネルギーが必要である。
そのため、エタンの基底状態エネルギー (8つの炭素原子の価電子+6つの水素原子) は、-29.29 -148.024 × 2 -13.606 × 6 = -406.974 eV となる。
(148.024 eV は炭素原子の 1-4th のイオン化エネルギーの合計である。)
ビリアル定理によれば、全位置エネルギー (tV) は、2 × -406.974 = -813.948 eV である。
C-C と C-H 結合長は それぞれ 15351 MM と 10940 MMである。 (1 MM = 10-14 meter).
また C-C-H 角は 111.7°である。
(Fig.40) エタン (H3C-CH3) の電子の周期的な運動。
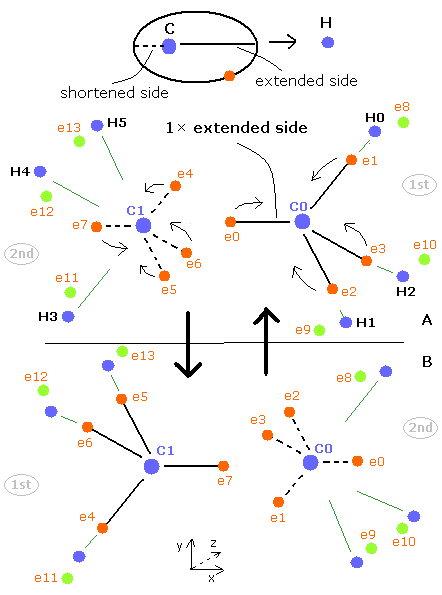
Fig.40 に示すように、エタン分子は 1st version と 2nd version のペアのメタンによって成り立っている。
2つの炭素原子核の間では、4つの電子が互いに避けながらもう一方の原子核にひきつけられている。
上記の メタンの C-H 結合と異なり、両方の炭素原子は 同じスピードと 同じ振動周期を持つ。
そのため できれば C-C 結合に関しては そのままの状態で考えるべきである。
ここでは、次のサンプル JAVA プログラムを使ってエタン分子を表現してみることにする。
( C-C、C=C 結合の本質 も参照のこと。 )
エタンのサンプル JAVA プログラム (ビリアル定理)
(もし中のプログラムをテキストエディタ(メモ帳など)にそのままコピー & ペーストすれば簡単にコンパイルして実行できる。)
このプログラムでは、中心電荷 (+4e = +6e -2e) を +4.22 としている。
つまり、もし”四面体構造”が完全に保たれると、ド・ブロイ波はちょうど 2.00 となる。
(Fig.41) エタン (H3C-CH3) の電子配置。
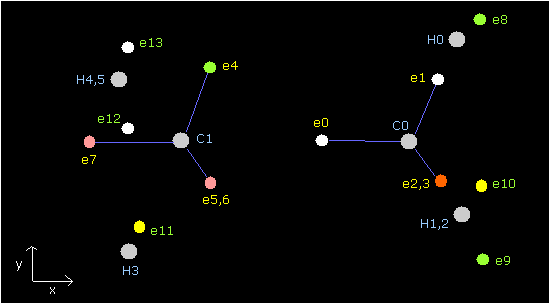
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6285 | 0 | 0 | 6285 | 1880 | 0 | 0 | 0 | 2.006 |
| ele 1 | 2305 | 6019 | 0 | 6445 | 1267 | -6 | 2 | 0 | 1.995 |
| ele 4 | 2235 | 6045 | 0 | 6444 | 2064 | 33 | -6 | -43 | 1.999 |
| ele 5 | 2235 | -3022 | -5235 | 6444 | 2064 | 33 | -34 | 27 | 1.999 |
| ele 6 | 2235 | -3022 | 5235 | 6444 | 2064 | 33 | 40 | 16 | 1.999 |
| ele 7 | -6360 | 0 | 0 | 6360 | 2116 | 0 | 0 | 0 | 2.006 |
| ele 8 | 1800 | 1825 | -3705 | 4505 | 1017 | -247 | -614 | -2 | 1.000 |
| ele 10 | 1800 | 2296 | 3432 | 4505 | 1017 | -247 | 309 | -530 | 1.000 |
| ele 11 | 800 | 1975 | 3900 | 4444 | 1416 | -172 | -298 | 0 | 1.000 |
Table 14 では、全位置エネルギーは -813.37 eV となり、これは実験値 -813.948eV とほぼ同じである。
電子 (8-13) と各水素原子核との平均距離は、(4505 + 4444) / 2 = 4474.5 MM, であり、これは ほぼ 4500 MM である。
もう一つの炭素の反発力のため、"正四面体"構造は少し壊れている。
ド・ブロイ波は 2.000 と少し異なる。(誤差は ± 0.005 ぐらいだ。)
C0 nuc、C1 nuc、H0 nuc に作用するトータルの力が ほぼゼロのときの条件を選んでいる。
H1 原子核に作用する力に関しては、CnH3 が できれば 400 以下になるようにする。
( この CnH3 は 各水素の電子の運動のため 正であるが、原子核の安定を考慮して できれば小さくなるべきである。)
次にスクロールバーの中から 16500 を選んで C-C (MM) ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6300 | 0 | 0 | 6300 | 2049 | 0 | 0 | 0 | 2.010 |
| ele 1 | 2315 | 6020 | 0 | 6449 | 1261 | -8 | 3 | 0 | 1.995 |
| ele 4 | 2290 | 6050 | 0 | 6468 | 2082 | 25 | -4 | -42 | 2.000 |
| ele 5 | 2290 | -3025 | -5239 | 6468 | 2082 | 25 | -34 | 25 | 2.000 |
| ele 6 | 2290 | -3024 | 5239 | 6468 | 2082 | 25 | 39 | 17 | 2.000 |
| ele 7 | -6380 | 0 | 0 | 6380 | 2119 | 0 | 0 | 0 | 2.016 |
| ele 8 | 1900 | 1600 | -3750 | 4498 | 1042 | -233 | -567 | -3 | 1.000 |
| ele 10 | 1900 | 2447 | 3260 | 4498 | 1042 | -233 | 287 | -489 | 1.000 |
| ele 11 | 800 | 1876 | 4110 | 4588 | 1358 | -158 | -234 | 1 | 1.000 |
基本的に、4つの核 (3つの水素原子核+他の炭素原子核) の反発力はつり合っており、炭素原子核は安定になる。
しかし、C-C 長がつりあいの長さよりも長くなると、他の炭素原子核の影響が弱くなる。(Fig.42 上)。
結果として、4つの反発力のバランスがくずれて、炭素原子核を安定化するためには (= C0,1 の FX,FY,FZ が小さくなる)、”正四面体”構造が より壊れてしまう。
Table 15 では、最大誤差が C0 の電子で 0.010、C1 の電子で 0.016 であり、これは control の Table 14 よりも大きい。
この 0.010 の値は小さくできない。
もし この誤差 0.010 を小さくしようとすると、ele1 の 1.995 を C0 原子核を安定にするために より小さくする必要がある。
また、全位置エネルギー (tV) は -806.74 eV であり、これは実験値 (-813.948 eV) よりも高い。
よって、Table 15 の C-C 結合は control よりも弱いことになる。
(Fig.42) エタン (H3C-CH3) の力のバランス。
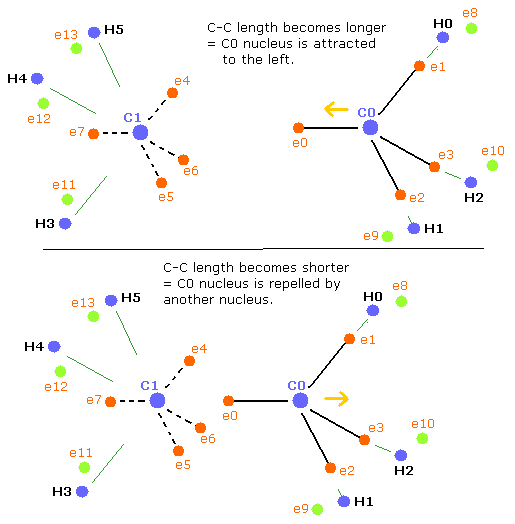
次に、スクロールバーの中から、 14000 の値を選び、C-C (MM) ボタンをクリックする。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6190 | 0 | 0 | 6190 | 1592 | 0 | 0 | 0 | 1.996 |
| ele 1 | 2350 | 6070 | 0 | 6509 | 1192 | -9 | 3 | 0 | 2.003 |
| ele 4 | 2235 | 6100 | 0 | 6496 | 1993 | 42 | -8 | -43 | 2.007 |
| ele 5 | 2235 | -3050 | -5282 | 6496 | 1993 | 42 | -33 | 29 | 2.007 |
| ele 6 | 2235 | -3049 | 5282 | 6496 | 1993 | 42 | 42 | 14 | 2.007 |
| ele 7 | -6280 | 0 | 0 | 6280 | 2188 | 0 | 0 | 0 | 1.991 |
| ele 8 | 1800 | 1825 | -3705 | 4505 | 1011 | -246 | -609 | -2 | 1.002 |
| ele 10 | 1800 | 2296 | 3432 | 4505 | 1011 | -246 | 307 | -526 | 1.002 |
| ele 11 | 800 | 1945 | 3800 | 4343 | 1470 | -174 | -327 | 0 | 0.999 |
C-C 長が つりあいのとれた長さよりも短くなると (Table 16 のように)、C0 原子核はもう1つの原子核によって反発力をより受けることになる。しかし一方で、C1 原子核は e0 電子により近づく。
つまり、C1 原子核は右に引き寄せられ、不安定になる。 (Fig.42 下)。
結果として、炭素原子核を安定にするために ( = C0,1 の FX,FY,FZ が小さくなる) は、”正四面体”構造がより壊れてしまう。
(Table 16 では、最大誤差が 0.009 であり、これは Table 14 の control よりも大きい。)
次にスクロールバーの中から 13500 を選び、C-C (MM) ボタンをクリックする。すると C-C の長さはさらに短くなる。
| eNo | X (MM) | Y (MM) | Z (MM) | nuc (MM) | CF | fx | fy | fz | Waves(wn) |
|---|---|---|---|---|---|---|---|---|---|
| ele 0 | -6180 | 0 | 0 | 6180 | 1354 | 0 | 0 | 0 | 1.987 |
| ele 1 | 2305 | 6095 | 0 | 6516 | 1190 | 2 | 0 | 0 | 2.007 |
| ele 4 | 2200 | 6200 | 0 | 6578 | 1934 | 55 | -10 | -46 | 2.024 |
| ele 5 | 2200 | -3100 | -5369 | 6578 | 1934 | 55 | -35 | 32 | 2.024 |
| ele 6 | 2200 | -3099 | 5369 | 6578 | 1934 | 55 | 45 | 14 | 2.024 |
| ele 7 | -6300 | 0 | 0 | 6300 | 2173 | 0 | 0 | 0 | 1.984 |
| ele 8 | 1800 | 1850 | -3680 | 4494 | 1011 | -247 | -623 | -1 | 1.000 |
| ele 10 | 1800 | 2261 | 3442 | 4494 | 1011 | -247 | 312 | -538 | 1.000 |
| ele 11 | 850 | 1980 | 3840 | 4403 | 1446 | -173 | -315 | 0 | 0.999 |
Table 17 では、C0 原子核は他の原子核によってさらに反発され、C1 原子核は e0 電子によってさらにひきよせられる。(Fig.42 下)
つまり、炭素原子核を安定にするには (= C0,1 の FX, FY, FZ が小さくなる)、"正四面体"構造が上の Table 14 のケースよりもさらに壊れる必要がある。
Table 17 では、最大誤差が 0.024 であり、これは Table 14 の control よりも大きい。
ここでは、水素の電子 11,12,13 は、 電子 8,9,10 よりも炭素原子核に、より近づくとしている。(Fig.40 上)
(そのため、ele11 の +X, +Y 座標は 正の数になる必要がある。)
しかし、ele 11 の +X を 負にしようとすると、nuc の値は短くなり、”平均の”nuc が 4500 MM よりも短くなる。
そのため、ele11 の +X, +Y は正にする必要がある。

2013/3/9 updated This site is link free.