トップページ ( ヘリウムも含む正確な新ボーア模型 )
ラザフォード (Mott) 散乱。
S行列
超ひも理論とループ量子重力は本当なのか?
標準模型は間違っている。
超対称性粒子は 時間と金の無駄遣い。
素粒子物理学の 標準理論による 素粒子の数は はっきり言って 多すぎるといえる。
クォークには 3世代 ( 1st, 2nd, 3rd ) ある。
そして 各世代にはそれぞれ 2つの異なったクォークが存在する(トータルは 3 × 2 = 6 クォーク )。
さらに 各クォークは パウリの排他原理に従うために 3つの異なる色 (赤、青、緑) を持つ必要がある。
(もちろん、各クォークは単離できないため、これらは単に推測にすぎない。)
驚くことに トップクォークは 素粒子にも関わらず 金の原子ほどの重さがあるのである!
(しかし 金の原子ほどの重さにも関わらず トップクォークの電荷は たった +2/3e なのである。)
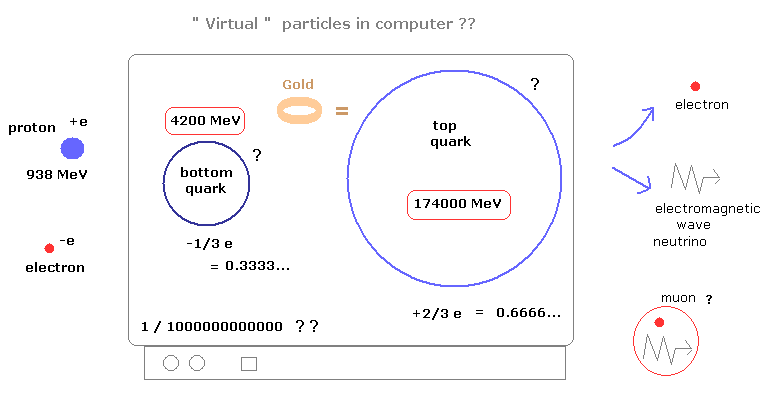
(Fig.1) コンピューターが作りだした "仮想"粒子か?

ご存じのとおり、奇妙なクォークは -1/3e や +2/3e などの 分数電荷を持っていると言われている。
電子は 素粒子の中で最も小さいものであり (= 0.5 MeV )、その電荷は 整数の -e である (分数電荷ではない!)
( それに 分数が許されるなら どうして +0.7e、-0.5e、+0.4e などはだめなのだろうか? 奇妙である。)
重要な点は クォークは単離することができず、また ゲルマン自身 クォークの実在性を信じていなかった。
あなたがたは 本か何かで よくあたりまえのように クォークはすでに見つかったというコメントを見たことがあると思われるが、これは 現在の標準模型とゲージ理論が正しいという前提条件があっての話である。
実在性の確かめられないクォークや分数電荷は 後で説明するが SU(2) や SU(3) などの ゲージ対称性という 極めて数学的な概念上の理論にとって 非常に好都合な存在なのである。
実際 原子核における ラザフォード散乱では 1/3 クォークの兆候を示しておらず、1/3 よりも小さいところに分布した曖昧な結果を与える。
もちろん、グルオンなども含めて これらは単離できないため まったくの推測にすぎない。
(Fig.1') 加速器内の不安定な粒子は 単なる”数式”なのか?
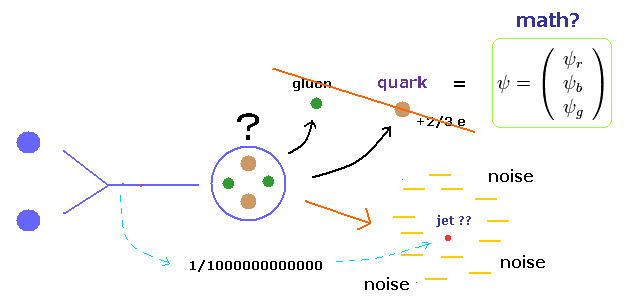
量子色力学 (QCD) は グルーオン や クォークを扱う分野だが、ご存じのとおり これらの粒子は 単離すること自体ができないため QCD 自体が 正しいか否か 確かめることができない。
最も重要な点は、加速器内の メソン、クォーク、W、 Z ボソン、ヒッグス粒子などの 様々な不安定な粒子は 何兆回もの衝突で ようやく 1つできるかできないかの 低確率なものだということである。
さらに これらの不安定な粒子は 直接観測することができず、単に 最終生成物から それらの存在を推定しているだけである。
これらの非常に不安定な粒子が 99.99% とか 5 シグマ の確率で 存在すると主張する前に、私達は それらの 極度に低確率な 生成確率について考慮すべきである。(= 1/1000000000000 以下 ).
もちろん これらの過程は すべてコンピューター処理化されているため これらは実は コンピューターが生み出した "仮想粒子" の可能性もあるわけである。
これらの事実を もっとはっきりと 一般の人たちに 説明すべきだと思われる。
(Fig.2) 誰が ミューオン を注文したの?
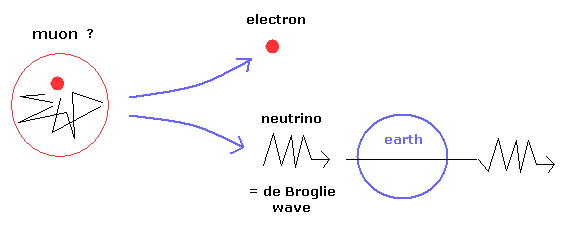
また 奇妙な素粒子ミューオンに関しても 当時の物理学者達が 「 誰が こんなもの (=ミューオン) を注文したんだ? 」と首をかしげた話は有名である。
非常に不安定なミューオンは わずか 2.2 マイクロ秒 で 電子とニュートリノに崩壊してしまう。
それにも関わらず ミューオンは 素粒子だと見なされている。なぜなのだろうか?
また これらの電子やニュートリノが どのような状態で ミューオンに詰め込まれているのか 私たちが質問すること自体を 現在の数学上の標準模型は 許していないのである。
つまり 明らかに現在の場の量子論は リアルな科学の発展を妨げているといえる。
高エネルギーの 宇宙線が 原子核を破壊して 電子や ドブロイ(縦)波を生じさせ、それらが一時的に絡まったものをミューオンとして扱っていると考えたほうが しっくりくる。
この高エネルギーのドブロイ波に絡まった状態では 一時的に 電子の質量と異なった振る舞いをみせている可能性がある。
また 相対論が間違っていたとしたら、ミューオンの寿命が延びる原因は 奇妙な時間の遅れによるものではなく その高エネルギーそのものによると 自然に解釈される。
(Fig.3) 昔のエーテル理論 ??
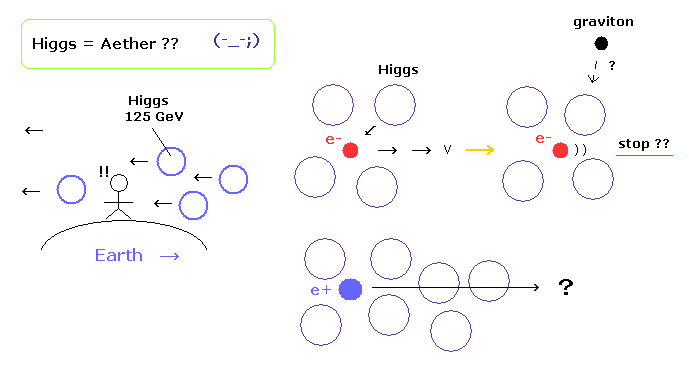
標準模型によれば、ヒッグス粒子は 全空間を埋め尽くしており、粒子の動きに抵抗 (= 質量 ) を与えるとしている。
つまり ヒッグスは 昔のエーテル理論に 似ているが、 彼らはこのエーテル理論を 決して認めようとはしない。
なぜなら ヒッグス粒子は エーテルを否定した相対論的なクライン・ゴルドン場をベースにしたものだからである。
しかし 空間を埋め尽くした これら無数の粒子は 相対論の "何も含まれない" 真空の概念と矛盾していると言わざるを得ない。
それに もし ヒッグスが抵抗として作用するなら 動いている電子は すぐに止まってしまう。これも奇妙である。
一方で 陽子の質量は ほとんどヒッグスの影響を受けない。はたして ヒッグス粒子は どのように これらの粒子を 区別しているのだろうか?
最も重要なことは ヒッグスと推定される粒子は 加速器内で 数兆回の衝突でようやく 1つ できるかできないかの割合なのである。
また ヒッグス粒子自体を直接観察することはできず、最終産物の一部とされる γ 線などの 少しの "excess" を見ているだけである。
もちろん このプロセスは 完全にコンピューター処理化されているため これら不安定な素粒子は コンピューターが作りだした 単なる”仮想”粒子 の可能性もあるわけである。
彼らは 無限のヒッグス粒子が 他の粒子を どう区別して 相互作用しているのかという 具体的なメカニズムの説明を避けているようである。
素粒子物理学で このような "Shut up and calculate ! " の姿勢を継続することは 私たちが 現在の標準模型が 単なる数学の産物 だと 認めていることと等価である。
(Fig.4) 加速器内の W ボソンは β崩壊のものとは異なるものである。
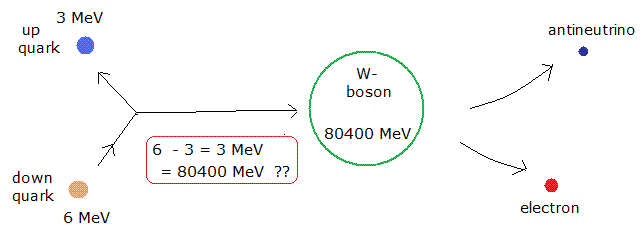
βマイナス崩壊では、中性子が 陽子と電子に崩壊するとき 非常に重い W ボソン を生成するとされる (= 陽子の約 80 倍の重さ )。
中性子と陽子の質量差は わずか 3 MeV 以下のため、この重い W ボソン (= 80400 MeV ) は 完全に エネルギー保存則を破っている。
そのため 彼らは 便利な量子力学の不確定性原理を用いて このエネルギー保存則の破れが説明できると言っているのである。
しかし こういった物理の基本的なルールを破る例外を認めることは 他にも不合理な奇妙な現象すべてを認めるというカタストロフィーに陥ってしまう。
もちろん ボーア・ゾンマーフェルト模型が 量子力学に置き換わることができたとしたら 不確定性原理自体が間違いということになり、この非常に重い W ボソンも間違いということになる。
( 問題は 一般の方々が 現在の標準模型が この不合理に重い W ボソンに頼っているという事実を知らないということである。)
(Fig. 4') ”仮想”粒子は 相対論に違反している。
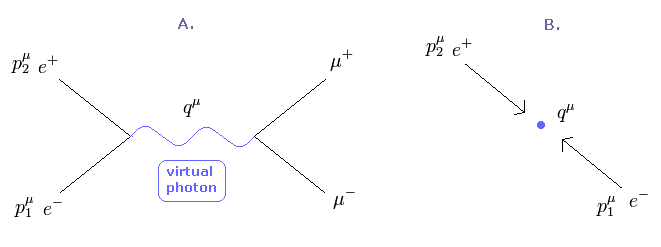
ご存じのとおり、粒子 (= 電子 ) と 反粒子が 融合して 光子 になるとき、その過程は 特殊相対論 (= 質量公式 ) に従わなければならない。
しかし 実際には 加速器内のすべての過程 ( クォーク、ヒッグス、ミューオン、W ボソン などの生成 ) は 特殊相対論に従っていないのである。
( 現在の素粒子論は 完全に 相対論的な場の量子論 をベースにしているにもかかわらずだ。)
例えば、Fig.4'-B の 重心系で、電子 (= p1 ) と 陽電子 (= p2 ) は 次の 4元運動量を持つとする。
(Eq.B-1)

"E" は エネルギー。 1-3 成分は 運動量で、重心系では それらはちょうど逆方向である。
エネルギー・運動量保存によれば、光子の 4元運動量は
(Eq.B-2)
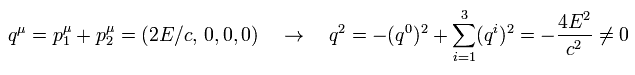
ご存じのとおり、特殊相対論によれば、光子の質量は ゼロにならなければならない。
( q0 = |q| → q2 = 0. )
しかし、Eq.B-2 によれば、この "仮想"光子の質量は 電子や陽電子よりも 大きいことになる。
これは 明らかに特殊相対論に違反している。
( Eq.B-2 は "スカラー"値なので すべての慣性系で 仮想光子は 相対論に違反する。)
このページに示したように、量子電磁力学は 様々な値を得るのに この奇妙な仮想粒子をうまく利用している。
素粒子論では、次の質量単位 ( ex. MeV/c2 ) を使う。
(Eq. 1) Mass unit.
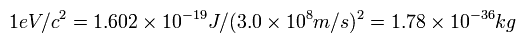
例えば、電子の質量は 次のように 0.511 MeV である。
(Eq. 2)
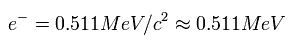
また 陽子の質量は 938 MeV、 ウィークボソンの質量は 80400 MeV、 トップクォークの質量は 174000 MeV (= 約 金原子 ) である。
(Fig.5) ヒッグス粒子は 電子、W,Zボソン、クォークなどが質量を持つのに必要不可欠である
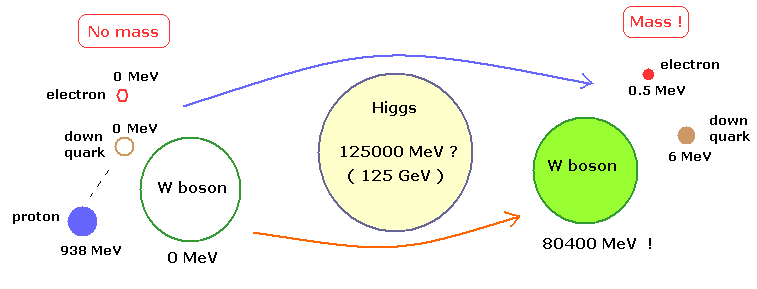
後で説明するが、ヒッグス粒子(ボソン)は 電子、クォーク、W,Zボソンなどが質量を持つのに必要不可欠な存在である。
( ただ 陽子の 98 % の質量は ヒッグス機構でなく グルーオンのエネルギーによるものである。)
そのため、もしヒッグス粒子が存在しなかったら、 この世界のあらゆるものが壊れてしまうことになる。
しかし、実は これらの奇妙な解釈は 対称性という 極めて実在性に乏しい "数学的な"概念のみに頼ったものである。
( 要するに 後で説明するが、これらの理論には "リアル"なイメージが存在しない。)
ヒッグス粒子の質量が もし存在するとしたら、だいたい 125000 MeV (= 125 GeV ) ぐらいで、これは 陽子の 125 倍にもなる。
奇妙なことに、私達は これら非常に重くかつ無限個存在する ヒッグス粒子をまったく感じることができない。なぜなのだろうか?
あなたがたは ニュースなどで よく ”ヒッグスが見つかった可能性は 99 % うんぬん”などと聞くことがあるだろう。
問題は この 99 % の数字が 何に対しての数字かということである。
彼らは 非常にやっかいな多くのバックグラウンドを除いて ヒッグスがないとしたときの状態を”推定”する。
そして この 99 % の数字を この推定したヒッグスなしの状態に対する 過剰な "excess" から計算するのである。
それに すでに述べたように ヒッグスとされる粒子は 数兆回の衝突で 1つできるかできないかのレベルなのである。
そのため、この推定した ヒッグスなしの状態の定義に応じて、当然 この計算値は 変化する。
さらに 標準模型は それらの質量を予測できない。( このページも参照のこと。)
(Fig.5') スピン 0 とは いったい何なのか ?
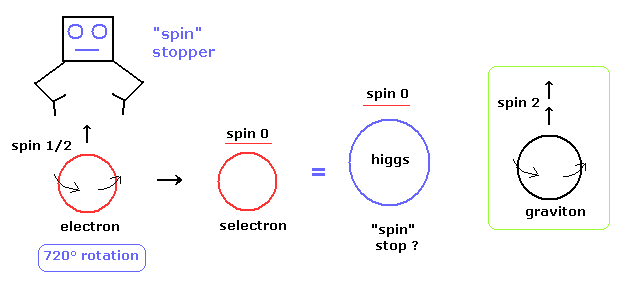
このページに示したように、スピンは非常に奇妙なものである。
ヒッグスは スピンゼロの粒子と言われている。
しかしもちろん、私たちは ヒッグス粒子の 回転している ( もしくは 回転してない ) 状態を直接見ることはできない。
( そもそも ヒッグス自体 直接観測できないもので、単に推測にすぎない。)
もし ヒッグスに スピンがないとすると、ヒッグスが崩壊後 生成された 新たな粒子が 様々な ( 一様な ) 方向へ 飛んでいく、と彼らは主張しているだけである。
もし 粒子に何らかのスピンがあるとすると、新たに発生した粒子は 崩壊方向に何らかの偏りがあることになる。
つまり "スピン" とは 単なる 崩壊パターンの偏りにすぎない。
非常に抽象的な概念であるスピンそのものに 明白な概念は何も存在しない。
しかし 彼らは好んでこの "スピン" というワードを使用したがる。なぜなのだろうか?
この スピンという用語の誤った使用が 一般の人々を 非常に惑わしていると思われる。
素粒子や標準模型を理解するには、"対称性" について 理解しなければならない。
なぜなら 4つの基本的な力 (重力をのぞいて) は この 対称性によって生じるからである。
( もし あなたがたが 標準理論に もっと明白なイメージを期待していたとしたら おそらくがっかりするだろう。)
U(1) ゲージ対称性は 電磁気力を生じさせる。
SU(2) ゲージ対称性は 弱い力を生じさせる。
SU(3) ゲージ対称性は 強い力を生じさせる。
そして フェルミ粒子や ウイークボソンが質量も持つには "ヒッグス 粒子" が 不可欠なのである。
( もし ヒッグス粒子が存在しなければ これらすべての粒子の質量は ゼロになってしまうのである。 )
ところで、この 対称性なるものの "物理的な意味" とは一体全体何なのだろうか?
残念ながら これら対称性なるものには 具体的なイメージがまったくない
つまり、これらは 単なる "数学上の産物" なのである。
このページでは このことについて 詳細に書いていくことにする。
(Fig.6) いかなる観測者も同じ物が見える=ゲージ対称性 ?

相対論によれば、すべての物理現象は いかなる観測者にも同じように見えなければならない。
この非常に厳しい制限のために 場の量子論のラグランジアンは ローレンツ変換不変なスカラーで かつ 無限種類の運動量とエネルギーを含まなければならない ( このページも参照のこと )。
もちろん、特殊相対論が間違いならば 私たちは これら非常に抽象的な数学上の世界に頼る必要はなくなる。
例えば、異なった位置や時間の観測者の視点 (= 空間、時間並進 ) から見ても 作用 S は不変でなければならない。
場の量子論によれば、これら並進(= 平行移動 )のもとでの 不変性が 運動量やエネルギー (= ハミルトニアン ) に関係している。
そのため 彼らは これらの概念を (局所)ゲージ不変性 などのような別のものにまで適用させ ボソンを介する力の関連性を説明するための道具にしたのである。
すなわち 相対論的な非常に厳しい制限のもとでは 彼らは 対称性(= 様々な変換のもとでの不変性 )と 物理的な実態 の関連性を探すことしか他に方法がなかったのである。
Eq.3 から Eq.8 (= 時間並進の一例 ) は この セクションに移動しました。
( ゲージ理論 = "数式" もしくは 物理 ? )
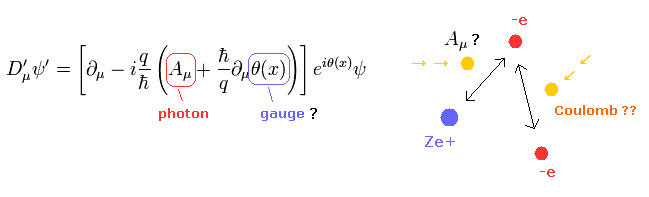
最初に、私達は 電磁気力の U(1) ゲージ変換について 理解する必要がある。
なぜなら、他の力 (弱い力や 強い力) は この電磁気力の理論をベースにしているからである。
残念ながら、QED は 単なる”数学的な”言語であり、かなり”限られた”数学的なツールしか持たない。
そのため、この理論を 他の力まで拡張させる以外 他に方法がないのである。
基本的な QFT に関するこのページをまだ読んでいなければ、先に読んでほしい。
自由粒子のディラック方程式に導く ラグランジアンは、
(Eq.9)
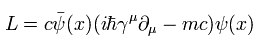
このラグランジアンは ローレンツ変換で不変でなければならない。
古典力学のラグランジアンとの 最も明白な違いは 場の量子論のほうは 物理的な実態が希薄だということである。
( つまり 場の量子論の ほとんどすべてのことについて 単なる "数学上" のルールとして考える必要がある。)
このラグランジアンは 次に示すように グローバルな位相変換で 不変 (= 対称 )である。
(Eq.10)

なぜなら この θ は xν (= 時間と空間 ) の変数を含んでいないからである。
グローバルな位相変換を考えるとき、ストレスエネルギーテンソルでの保存量は ”電荷 Q”になる。
( もちろん 場の量子論の定義した電荷のことである。 )
このように 彼らは 様々な変換のもとでの ラグランジアン(作用)の不変性を 何らかの物理的な概念を得るための ツールとして使用するようになったのである。
非常に厳しい相対論による制限のもとでは、これらの対称性のツール は 弱い力や W ボソンのSU(2) や、クオークの SU(3) などの 数学上の存在を生み出したのである。
この θ が xν の変数を含むとき、 この変換は ローカル (局所的)な位相変換という。
この θ中の xν 変数のために、 Eq.9 のラグランジアンは微分によって変化してしまう。
(Eq.11)
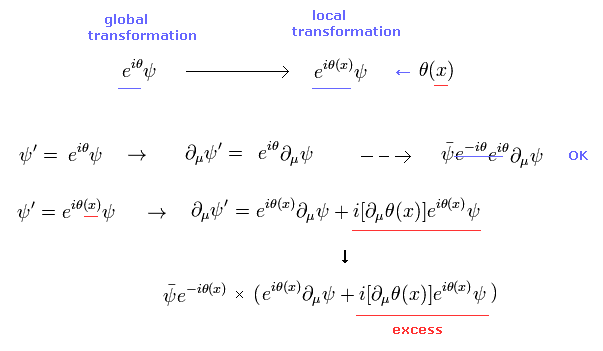
つまり、Eq.9 のラグランジアンは ローカル変換に対して 不変ではないということになる。
ローカルな位相変換で不変 (= 対称的) にするためには、Eq.9 の自由粒子のラグランジアンに 4元ポテンシャル ( Aμ ) を付け加える必要がある。
(Eq.12)
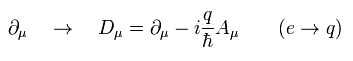
電子を扱いたい時は、この "q" を "-e" に変更するように。
これは 共変微分と呼ばれる。 そして ベクトル(もしくは スカラー) ポテンシャル Aμ は "ゲージ場" と呼ばれれ、光子を意味している。
このページ (Eq.2-16)に示したように、この共変微分は もともと古典的な ローレンツ力からきている。
さらに 電場 (= E ) や 磁場 (= B ) は Eq.14において 任意の θ を選んでも変化しない。
(Eq.14)

つまり この θ は 実際に観察されるものではない。 しかし 彼らはこれを最も重要な概念と考えているのである。
Eq.12 や Eq.14 を使うと、ラグランジアンの微分 ( Eq.9, Eq.11 ) は次のようになる。
(Eq.15)

θ の係数の調整は 少し数学上の技巧のように思えるが・・。
結果として、ローカルな位相変換においても 次のように 不変となる。
(Eq.16)

( もちろん Eq.9 の ラグランジアン の質量項においても 不変になる。 )
Eq.12 の共変微分を使うと、ラグランジアンは、
(Eq.17)
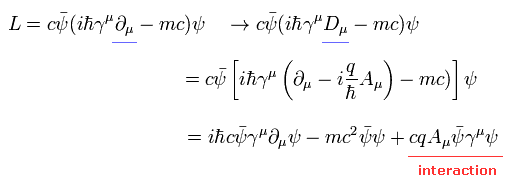
このセクションで示したとおり、彼らは ある変換のもとでの不変性 (= 対称性 ) を 物理的な何かの概念に 結びつけることしかできないのである。
これが 相対論的な場の量子論の実態である。
このページ (Eq.3-1)に示したように、 ベクトル(もしくは スカラー)ポテンシャルの 反対称テンソル ( Fμν ) は、
(Eq.18)
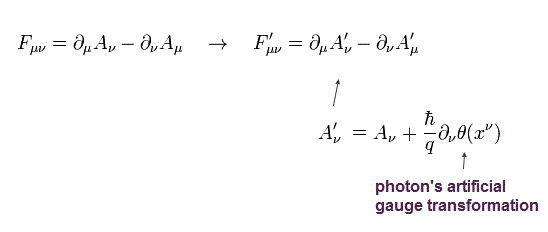
Eq.14 のゲージ変換を Eq.18 に代入して、
(Eq.19)
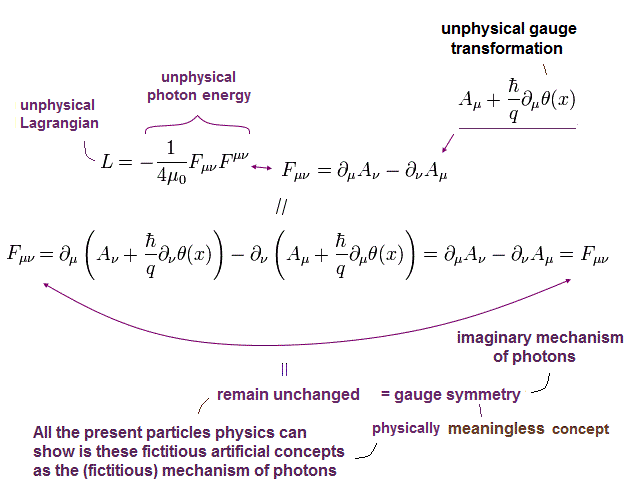
つまり、この反対称テンソルは ゲージ変換で不変である。
結果として、マクスウェル方程式のラグランジアンも 次のように 不変である。
(Eq.20)
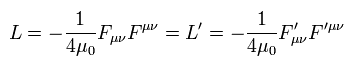
( 質量項は "対称性" を阻害する。 )

しかし もし光子が 質量を持つとすると、 このラグランジアンは クライン・ゴルドン場のラグランジアンのように AμAμ 項を含む必要がある。
この項は Eq.14 のゲージ変換で 不変ではない。
(Eq.21)
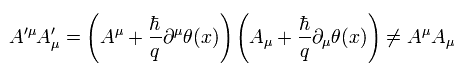
つまり、光子に質量があると、マクスウェル方程式のラグランジアンは ゲージ変換で不変ではなくなるのである。
(Eq.22)
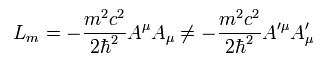
だから、光子には質量がないと彼らは主張しているのである。
あなたがたは この非常に "抽象的な" 理由をよく理解できただろうか?
残念ながら これらの理論は 実態のない数式をいじっているだけである。
問題なのは これらを拡張して 想像上の粒子 W ボソン (= エネルギー保存則の破れ ) や クォーク (= 単離できない ) を 生み出してしまったことである。
(Fig.7) 光子のサマリー。

しかし 非常に重い W ボソンの場合は ”質量項”を持つ必要がある。
( W ボソンは 荷電粒子のため 質量ゼロはあり得ない。)
すると、ゲージ変換 (= SU(2) ) のもとで、W ボソンのラグランジアンは 不変ではなくなる。
この状況を避けるために 彼らは ヒッグス場を導入して 重い W ボソンの質量を ゼロにしたのである。
これが ヒッグス粒子が必要となった主要な原因である。
( W ボソンのラグランジアンの代わりに、ヒッグスの式が W ボソンの質量項を含む。)
( W ボソンの質量? )
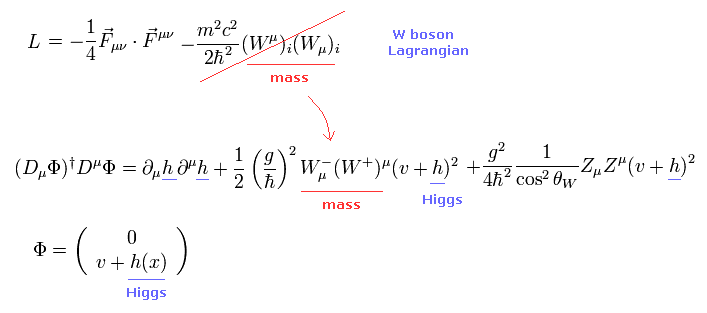
残念ながら、一般の方々は これらの非常に抽象的な理由をよくご存じない。
彼らは 一般の人たちに これらの抽象的な概念を説明すべきであると思われる。
要するに "数学上"の対称性が 現在の標準模型にとって 非常に重要なものなのである。
素粒子間の 相互作用や反応を考えるとき、Eq.17 のような相互作用項を使用する。
( このページも参照のこと。 )
(Eq.23)
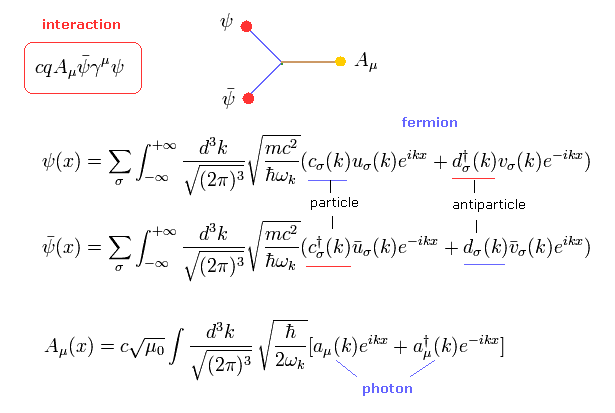
また 次の 粒子 (= c ) と 反粒子 (= d ) の反交換の関係を使用する。
(Eq.24)

Eq.24 以外の組み合わせは 真空 (= < 0| |0 > ) に挟まれて 消えてしまう。
例えば、消滅-消滅 ( c - c や d - d )、 生成-生成 ( c† - c† ) の演算子の組み合わせは消えてしまう。
つまり 次の組み合わせが 生成消滅因子間の関係から許されることになる。
(Eq.25) 粒子生成+反粒子生成 =○。
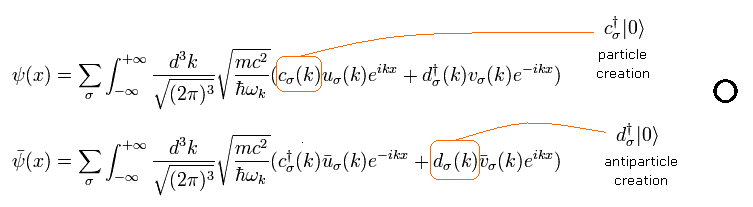
しかし 次の組み合わせは許されない。
(Eq.26) 粒子生成+粒子生成 =×。
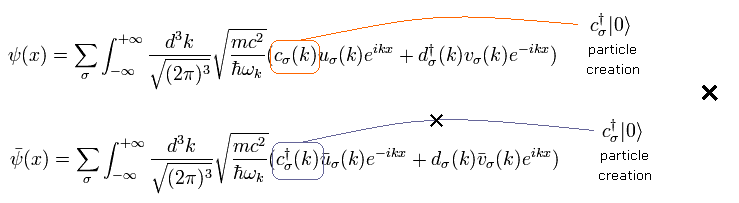
例えば、次の β- (ベータマイナス) 崩壊の反応を考える。
(Eq.27)
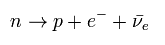
ここでは 中性子は 陽子、電子 反ニュートリノに崩壊する。
( 上記の相互作用項によれば ニュートリノではなく 反ニュートリノになる。)
また β- 崩壊は 光子 (A) の代わりに W ボソンを 相互作用項に使用している。
Eq.27 のダイアグラムは、
(Eq.28)
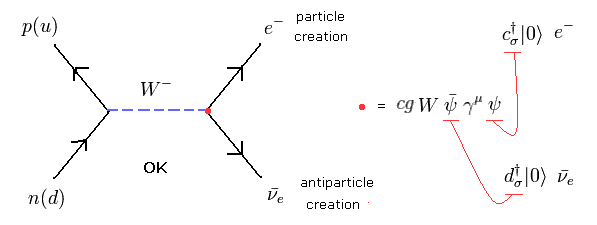
Eq.25 や Eq.26 と似た理由により、 反ニュートリノ と電子 (= particle ) の生成が許されている。
しかし 次の反応 (ニュートリノと電子の生成) は許されていない。
(Eq.29)
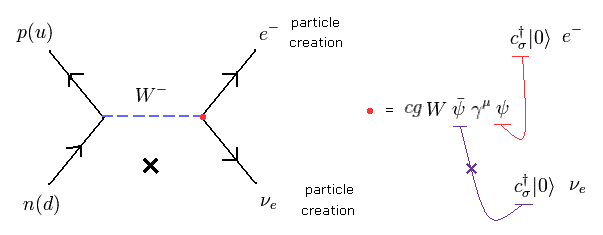
もちろん、私たちは ニュートリノと反ニュートリノの区別をはっきりつけることはできない。
これは 単純に "数学的な" 理由によるものである。
ある静止した電子 (= p ) が 1つの光子 (= q ) を吸収して p' の電子になったとする。
(Eq.30)
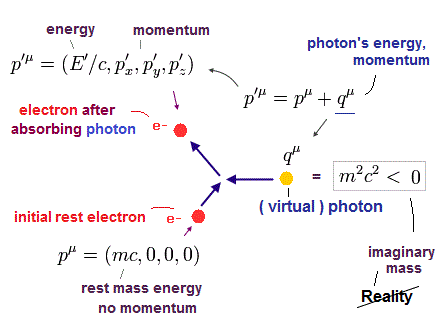
静止した電子 (= p ) のエネルギーは 静止質量エネルギー ( E/c = mc ) のみである。
( つまり この静止した電子の運動量はゼロである。)
光子のエネルギーを吸収したあとの p' の電子には 運動量がある。
相対論によれば、光子との相互作用の十分に前と後では 次の関係式が満たされる必要がある。
(Eq.31)

ここでは (-1,1,1,1) バージョンの計量テンソルを使用している。
つまり Eq.31 はマイナスにならなければならない。
Eq.30 と エネルギー運動量の保存より、光子のエネルギーと運動量は、
(Eq.32)
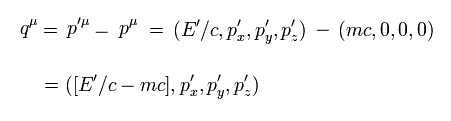
ご存じのとおり 光子の質量はゼロである。しかし Eq.32 によれば、
(Eq.33)
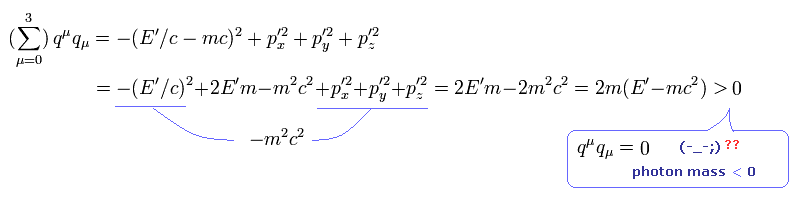
Eq.33 は 光子の質量が マイナスであることを意味し、これは相対論に明確に反している。
結果的に 相対論における2乗のエネルギーと運動量の関係式は 自己矛盾を含んでいることになる。
そのため 彼らは 非常に奇妙な概念である 仮想粒子なるものを導入した ( この場合は 仮想光子ということになる )。
また このページに示したように、特殊相対論は 電磁気学で破綻している。
もちろん 電荷と電流の関係は いかなる慣性系でも保たれる必要があるため、ローレンツ変換自体が間違いということになる。
(Fig.8) 相対論の厳しすぎる制限 → モデルの抽象化、数学化。

実際に ローレンツ対称性を完全に順守するには、私たちは通常の原子、分子模型をあきらめなければならない。
要するに、Fig.8 右 のような かなり”制限された”数学上の模型しか使用できない。
そのラグランジアン (= L ) は ローレンツ変換で スカラー、かつ その関数もローレンツ対称性に従わなければならない。
この純粋相対論的な制限された世界では、1つの粒子が生成 (もしくは 消滅)されるときは それが全空間に同時に起きなければならない。
また ローレンツ対称性をキープするためには、それは必ず 無限大から無限大の全種類の運動量を含まなければならない。これは深刻な発散問題を引き起こす。
(Fig.9) エーテルなし = 仮想光子のモデルは相対論を破っている。

特殊相対論は "エーテル"を禁止しているため、”クーロン力”を説明するためには 何か別のものを使う必要がある。
上で述べたように、たとえ 相対論の非常に厳しい制限を順守しようとしても、仮想光子は 相対論を満足しない。
また 驚くべきことに、特殊相対論は この奇妙な仮想光子を "クーロン力の媒介物"として採用しているのである。
Fig.9 に示すように、あるエネルギーを持った仮想光子は 真空から 突然現れる。
このプロセスは エネルギー保存則を破っている。
この仮想光子が 相手の荷電粒子に到達して初めて 荷電粒子は "クーロン力" (= 仮想光子の運ぶエネルギー) を受ける。
( 単一電子が 仮想光子を介して 他の荷電粒子を感じることができなければ、そのエネルギーや運動量は変化しない。)
結果的に、たとえ 非常に厳しい相対論的な制限を順守しようとしても、それは不可能である。
(Fig.10) 場の量子論における 一般相対論の制限は アインシュタインの重力理論の関係を壊す。

上で述べたように、ローレンツ対称性を保つためには、相互作用項が 無限種類の運動量を含む必要があり、これが発散につながる。
このページに示したように、QED の場合は 無限の裸の電荷を仮定したなら、発散は 電荷の中に繰り込むことができる。
もちろん、この考えは理不尽である。 実際、パウリやディラックは繰り込みを嫌っていた。
後で説明する 質量ゼロの W ボソンの相互作用も 光子に似ているため 繰り込み可能である。
一般相対論 ( このページも参照のこと ) では、”複雑な”クリストッフェル記号や共変微分は、場の量子論において さまざまな発散を引き起こす。
( 場の量子論では 微分は指数関数との組み合わせで 運動量 (= 無限大から無限大の) を意味する。)
これらのやっかいな発散を取り除こうとすると、あらたな相互作用が発生してしまう。(= Fig.10 右 )
これはつまり これらを繰り込もうとすると、"巨視的な重力の関係式が壊れてしまう" ことを意味する。これは深刻である。
つまり 一般相対論では 繰り込み手法が使用できない。
このことが 10次元の奇妙な超ひも理論を生み出すことになった。
βマイナス崩壊では、 中性子は、陽子、電子、反ニュートリノに崩壊する。
遊離した中性子は 準安定 (= 半減期が約10分)である。
つまり 何らかの弱い力が この反応に関係しているといえる。
もちろん 陽子と電子は クーロン力 (= 光子)で 互いに引き合っている。
この引力にも関わらず、中性子は崩壊する。
(Fig.11) β- 崩壊 (中性子 → 陽子 + 電子 + 反ニュートリノ )
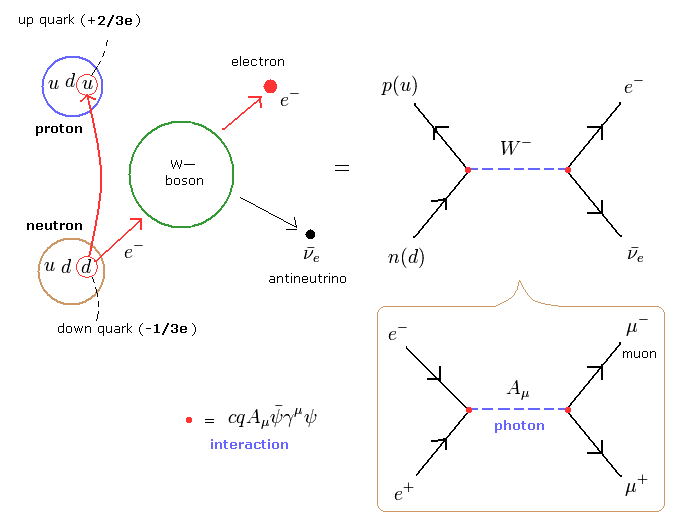
QED においては、すべての反応を 相互作用項とファインマンダイアグラムで表さなければならない。
W - ボソンは 負の電荷 を運ばなければならないため、中性の ベクトルポテンシャル 光子 ( = Eq.23) を 相互作用項で使うことができない。
これが "弱い"力が誕生した理由である。
( 端的に言えば 場の量子論における "数学上"のルールが 新しいウィークボソンを必要としたのである。)
標準模型によれば、中性子の ダウンクォーク (= -1/3e ) が 電子 (= -e ) を放出して 陽子の アップクォーク (= +2/3e) になるとしている。
つまり、全電荷が保存されることになる ( -1/3e = +2/3e + (-e) )。
( ダウンクォークは 標準模型によれば 素粒子であり、もちろん それ以上 分割することができないはずであるが・・ )
この 重い W- ボソンは Fig.4 で述べたように、完全に エネルギー保存則に違反している。
(Fig.12) β - 崩壊 ( ニュートリノ = 残りのドブロイ波。 )
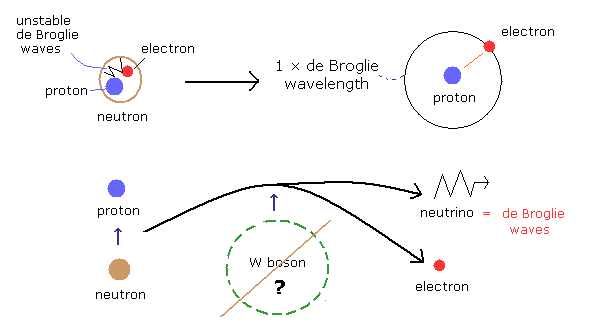
ボーア模型では、電子は 基底状態のとき (= 1 × ド・ブロイ波長) よりも 原子核に近寄ることができない。
電子のエネルギーが大きくなるにつれて、ド・ブロイ波長は短くなる。
安定な原子核においては、捕獲された電子の 非常に短いド・ブロイ波が なんらかの理由で安定になると考えられる。
しかし、孤立した中性子においては、この電子のド・ブロイ波が 不安定になり、その不安定性が それらのクーロン引力に勝ってしまい、電子と陽子が遊離してしまうと考えられる。
また、ニュートリノが 簡単に地球を通り抜けるなどの性質があることを考慮すると、ニュートリノ( もしくは 反ニュートリノ )を ある種の 残りの ド・ブロイエネルギー波のようなもの と考えるのが自然である。
つまり、弱い力や ウィークボソン ( あるいは ヒッグス粒子 ) のような 奇妙な概念をわざわざ導入する必要がない、と私は思う。
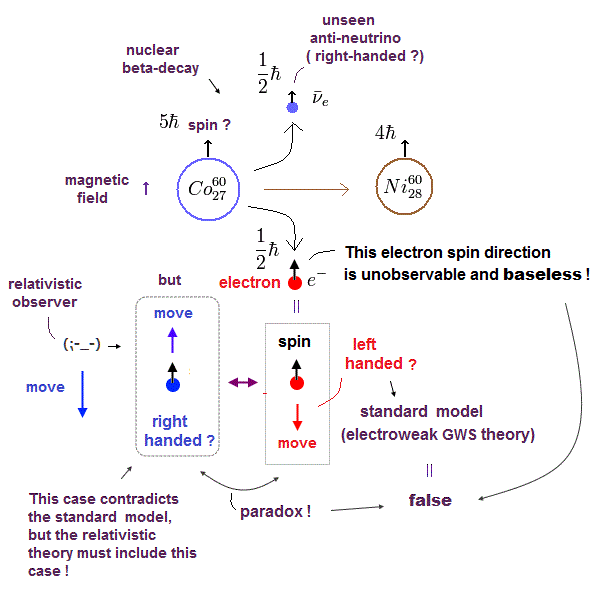
(Fig.13) β-崩壊の電子は 左巻き?
空間反転のもとでは、位置や運動量ベクトルなどは マイナスになる。
また 角運動量 (= r × p ) は不変のままである。
(Eq.34)
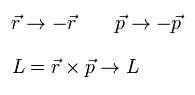
いかなる観測者からも 同じに見える 相対論的なラグランジアンでは この空間反転の状況においても 不変でなければならない。
そのため β-崩壊において コバルト(Co)-60 の原子核スピン (= 角運動量) の方向に関わらず、電子がこの核のスピンに関して 両方向に飛んでいく確率は同じにならなければならない。
( 空間反転のもとでは、Co-60 のスピンは不変で、電子の運動量は逆になる。)
外磁場 (= z 方向) のもとでは、Co-60 のスピンは z 方向を向く。
しかし この場合は、電子は マイナス z 方向へ飛んでいく傾向がある。
Co-60 と Ni-60 スピンの違いは ħ である。そのため 電子スピンの方向は その運動量と逆になる (= 左巻き )。
( もちろん これらスピン角運動量は このページに示したように量子力学的な定義によるものである。 )
反ニューリノは 右巻きであるため、ニューリノも β-崩壊においては 左巻きである。
(Eq.35) 左巻きと右巻きの電子への分離。
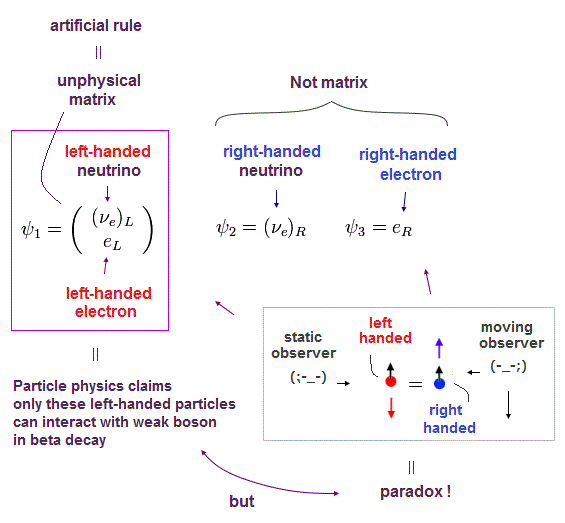
そのため 彼らは "人為的に" 電子 (や ニュートリノ) を Eq.35 に示すように 左巻きと右巻きに分離した。
奇妙なことに 左巻きのみが 2 × 1 のスピノルであり、このことが ゲージ変換不変性を維持するために フェルミ粒子の質量をゼロ にしてしまった。
( そして これらフェルミ粒子も 後で説明するが ヒッグス機構が必要になる。)
しかし 単純に古典力学的な視点からみると、外磁場 (= 原子核スピン) の向きと 同じ向き、逆向きに 電子が崩壊後 飛んでいく確率が違っていることは別に自然といえる。
( 逆に 異なった状況なのに 確率がまったく同じほうが不自然である。)
相対論的な場の量子論の 非常に制限された枠の中では、彼らは Eq.35 の不自然な考え ( 1つが 2 × 1 のスピノル、もう1つが数 ) を採用するしか他に方法がなかったのである。
(Eq.35') どうして ±W と Z ボソンが必要なのか?

後で説明するが、ディラック方程式は 1つの式の中で 左巻きと右巻きのスピノルに分離できる。
つまり 左巻きのスピノルのみをピックアップするには、”質量項”を消去して それを ヒッグス機構に移す必要がある。
しかし このケースでは 本来対称的である電磁気力 (= 光子 Aμ ) までもが パリティーが破れてしまう。
それを避けるために、彼らは 中性の Z 粒子なるものを導入したのである。
これらの不安定な W と Z ボソンは 直接 観測することはできない。 単に 最終生成物であろうとされる 電子などを見て それらの存在を推定しているだけである。
弱い力を導入するには、行列を使わなければならない。
なぜなら そこに 光子 (= A )、±W、Z ボソン の4種類の力を 詰め込む必要があるからである。
もちろん、この形式は 上で述べた ベクトルポテンシャル A の形式を模倣する必要がある。
彼らは 電磁気 ( 光子 ) の 美しい対称性を 他の力まで拡張しようとしたのである。
弱い力を表すスピノルは、
(Eq.36)

この 各 ψ1 と ψ2 は 次に示すように 4 × 1 行列である。
(Eq.37)

つまり、Eq.36 は 奇妙な 8 × 1 行列ということになる。
Eq.36 の 共役な転置行列 (× γ0 ) は、
(Eq.38)
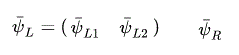
これは 1 × 8 行列である。
弱い力のラグランジアンは、
(Eq.39)

これは ”数学的に”少し複雑である。
(Eq.40) パウリ行列。
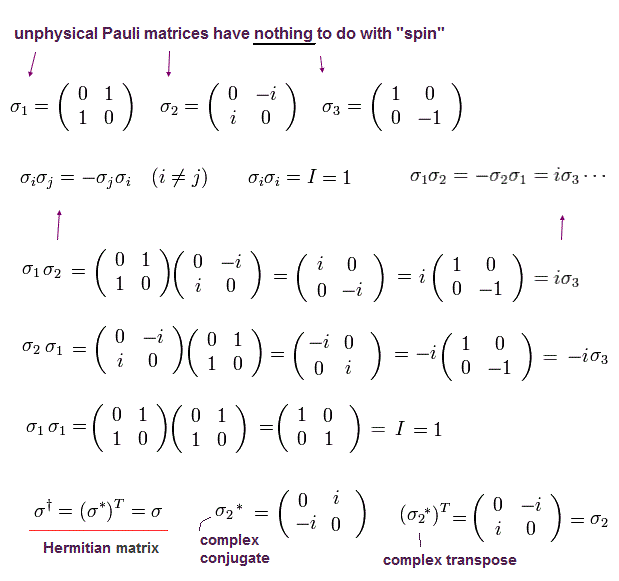
ここでは パウリ行列を使用した。
しかし 弱い力において パウリ行列の物理的な意味は 特にないと言っていい。
標準模型では 特に物理的な意味を問うことなく 様々な数式を取り入れているといえる。
パウリ行列は エルミト行列で かつ 群論にとって 都合のいいことだけである。
電磁気力の ローカルな位相変換は Eq.11 である。
弱い力のそれに相当するものは、
(Eq.41)

この位相変換がどうして突然現れたかという 明確な理由はとくにないことを心に留めておく必要がある。
電磁気力と異なり、Eq.41 は パウリ行列のために 2 × 2 行列になっている。
( 最初に、θ のみ x の変数を含んでいないとする。)
Eq.40 の エルミト行列の性質により、Eq.41 は つぎのように "ユニタリ" となる。
(Eq.42)
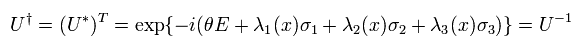
Eq.41 の成す群を SU(2) と呼ぶ。
そのため 弱い力の ローカルな位相変換は、
(Eq.43)
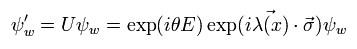
ここで Eq.43 の位相変換のもとでの 不変性を目指す。
弱い力の 共役微分は、
(Eq.44)

ここで σ は パウリ行列である。
Eq.44 は 電磁気力の Eq.12 に相当する。
(Eq.12)
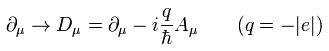
Eq.39 のラグランジアンを ローカルな位相変換で不変にするには、次の関係を満たす必要がある。
(Eq.45)

これは 電磁気力の Eq.15 に相当する。
Eq.43 と Eq.44 を使って、
(Eq.46)

Eq.45 の関係式を満たすには、 Eq.46 の W' は 次を満たす必要がある。
(Eq.47)
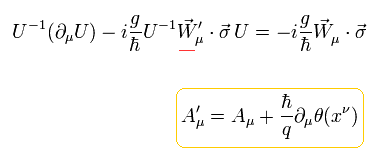
これは少し複雑である。しかし Eq.47 は 電磁気力の Eq. 14 に相当するゲージ変換である。
Eq.39 において 共変微分 Eq.44 を使うと、 ラグランジアンは、
(Eq.48)

Eq.48 の最後の項は、フェルミ粒子とウィークボソンの相互作用を意味している。
次に マクスウェル方程式のラグランジアンである Eq.20 に相当する ウィークボソンのみのラグランジアンを考える。
(Eq.49)

これは 内積である。
マクスウェルのラグランジアン (= Eq.20 ) と 弱い力のラグランジアン (= Eq.49 ) の最も重要な違いは、マクスウェルのラグランジアンのみ オイラー・ラグランジュ方程式を解くことによって 実在のマクスウェルの方程式を得られるということである。
弱い力のラグランジアンには マクスウェルのような意味はない。
電磁気力のケースでは、反対称テンソル (= Fμν ) は Eq.12 の 共変微分を使って次のように表せる。
(Eq.50)

Eq.50 のように、次のように 弱い力の反対称テンソルを定義する。
(Eq.51)
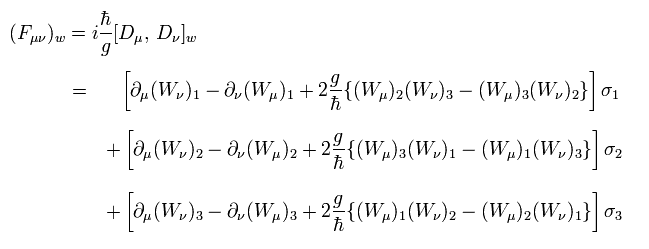
ここでは パウリ行列における Eq.40 の関係式を用いている。
例えば Eq.44 を使って、Eq.51 の 1 成分の計算では、
(Eq.52)

Eq.52 は パウリ行列を含んでいるため 少々複雑である。
( もちろん ここには 物理的な意味は特にない。ただ計算するだけである。)
Eq.51 は 単純に次のようにかける。
(Eq.52')
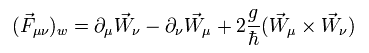
上に示したように、W' が Eq.45 を満たすとき、次の関係式が得られる。
(Eq.53)
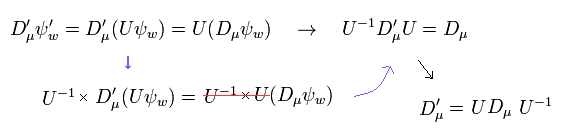
つまり、ゲージ変換後の 反対称テンソルは、
(Eq.54)
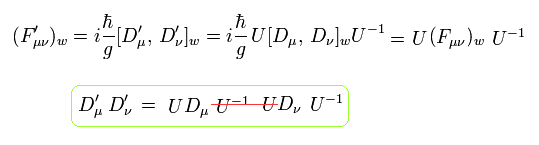
ゲージ変換後のラグランジアンは、
(Eq.55)
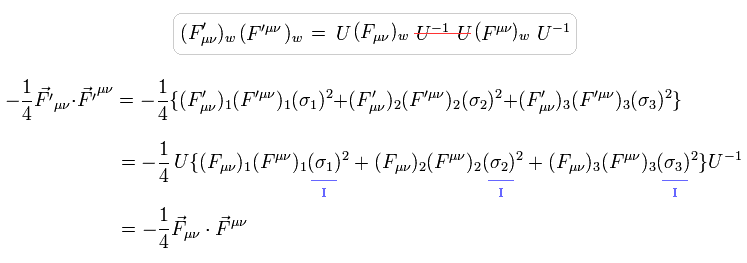
ここでは Eq.40 と Eq.54 を使っている。
結果として、Eq.41 のゲージ変換で ウィークボソンのラグランジアンは不変である。
( もちろん 不変になるように Eq.47 と Eq.51 を "人為的"に 定義したのである。)
しかし 電磁気力と異なり、ウィークボソンは 大きな質量を持つ必要がある。
( また 荷電粒子 ±W ボソンの質量は ゼロには なれない。)
なぜなら その質量がゼロだと、弱い力は 電磁気力のように 遠くまで作用することになるからである。
つまり、ラグランジアンは 次の 質量項を持たなければならない。
(Eq.56)

Eq.56 に示すように、この質量項は Eq.47 のゲージ変換で 不変ではない。
( これは Eq.21 と Eq.22 に類似している。)
もし Eq.47 が "excess" の部分を含んでいなければ 不変になる。
そのため、対称性の理論によれば ウィークボソンの質量は ゼロにならなけらばならない。
その代わりに、ヒッグスボソンが ウィークボソンに質量を与えるものとして 重要になってくるというわけである。これについては 後で説明する。
( W ボソンの質量項が ヒッグスの式に移された。)
お気づきのとおり、これらの理論には まったくといっていいほど 具体的なイメージなどは存在しない。
ディラック方程式に質量がないとき、それは左巻きと右巻きの状態に分離できる。( このページも参照のこと。)
ここで 左巻きと右巻きのスピノルについて簡単に説明する。
"右巻き" とは スピンと運動量の方向が同じで、”左巻き”とは それらの向きが逆だという意味である。
( もちろん、これらは 物理学的な実態というよりも 数学上の定義と言える。)
(Eq.57)

γ5 行列に対する 左巻きのスピノルの固有値は " -1 "。
また 右巻きに対する固有値は " +1 " である。
Eq.57 より、粒子に質量があるとき、左巻きと右巻きのスピノルは 1つのディラック方程式の中で ミックスされる。
(Eq.58)
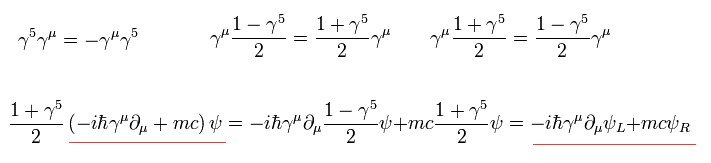
Fig.13 で述べたように、β-崩壊では パリティー不変性が破れている。
そのため 彼らは フェルミ粒子を 左巻き (= 2 × 1 行列 ) と 右巻き (= 数 ) のスピノル (= Eq.59、Eq.60 ) に分離したのである。
つまり ゲージ変換の”形”も これらのスピノルで異なることになる。
結果的に Eq.58 のミックスした式において ゲージ変換で不変になるには、それらフェルミ粒子の質量は すべてゼロにならなければならない。
これが ヒッグス機構が必要になった理由である。
これらの考えに基づいて、弱い力の波動関数は 次のように分離できる。
(Eq.59)
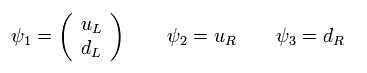
uL と dL は それぞれ "左巻きのアップクォーク" と "左巻きのダウンクォーク" である。
重要な点は Eq.59 の ψ1のみ 2 × 1 行列だということである。
(これは ちょっと想像するのが難しいが・・。)
また、レプトンは、
(Eq.60)

Eq.44 のかわりに、次の共変微分を使う。
(Eq.61)
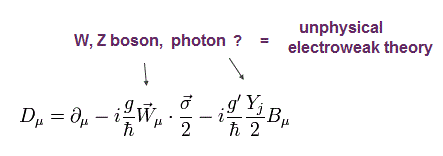
ここで Bμ は 光子に関係しており、また Yj は "ウィークハイパチャージ" なるものである。
( 非常に"人為的なもの" である。)
Eq.61 を使って、 ラグランジアン ( 質量項を除いた ) は、
(Eq.62)

重要な点は、Eq.61 のパウリ行列は Eq.59 ( Eq.60 ) の ψ1のみに作用するということである。
これは 単なるルールであるため、従わなければならない。
Eq.40 のパウリ行列を用いて、
(Eq.63)
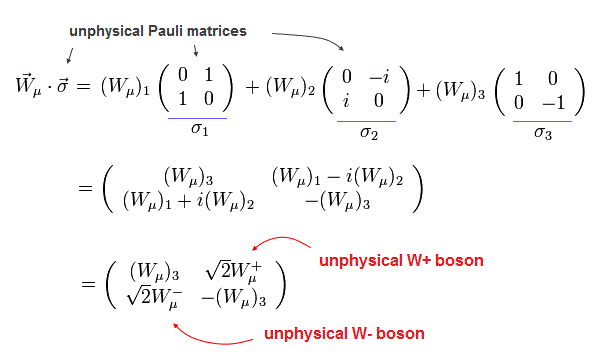
ここで W± ボソン を次のように定義する。
(Eq.64)

± は W ボソンの反対電荷を意味する。
これも 単なるルールである。 これらの ± が 電荷を表す明白な理由は何もない。
Eq.64 を使って、Eq.63 は
(Eq.65)

Eq.64 を使って、Eq.62 の2行目は、
(Eq.66)
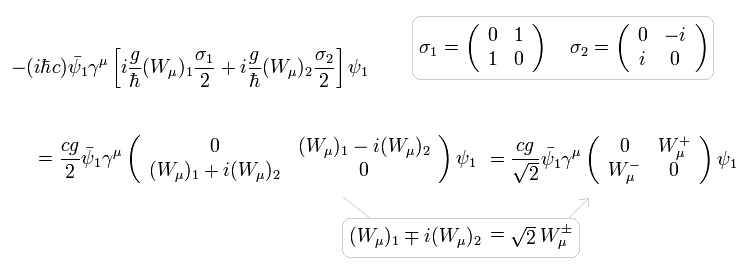
この定義に基づいて、 W3 と B の両方は 電荷なしということにする。
また 光子のように W ボソンも質量を持たない。
( もちろん 荷電粒子 ±W ボソンで 質量ゼロはあり得ない。そのため ヒッグス機構が必要なわけである。)
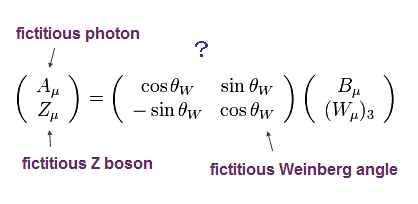
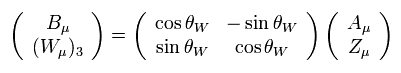
Eq.67 の人為的な定義は 残りのゲージ W3 を処理しながら 光子の相互作用項を得るためのものである。
もし この新たな中性粒子 Z がないと、本来対称的である 光子 A (= 電磁気力 ) までもが W ボソンのように パリティーが破れてしまう。
しかし 今までご覧になったとおり、私達は ”局所ゲージ対称性”の 物理的な実態の意味を しっかり問うことなく 議論を進めてきたわけで、この結果が Eq.67 の数学上の定義につながったのである。
Eq.68 を Eq.62 の第3項目に代入して、
(Eq.69)
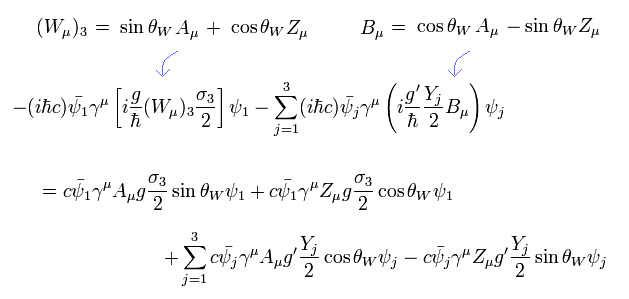
ここで ウィークアイソスピンの第3成分 (= T3 ) という新しい概念を導入する。
(Eq.70)

ウィークアイソスピンは普通のスピンと異なる。
uL と dL の ウィークアイソスピンの第3成分は それぞれ +1/2 と -1/2 である。
そして 右巻きのフェルミ粒子の ウイークアイソスピンはすべて ゼロである。
それなのに 通常のパウリ行列 (= σ3 ) が使用されている。
2 × 1 行列中の W3 を 右巻きフェルミ粒子に組み入れるために、右巻きのアイソスピンのみがゼロになるというわけである。
これは ちょっとできすぎである。
自然界の法則 は 本当に これら”数学上”の定義に従っていると思われるだろうか?
( "スピン" と "運動量" の方向は それほど重要なのか ?? )

右巻きと左巻きの違いは 単に 移動方向のみである。
例えば、右巻きの粒子が 北方向に飛んでいると、左巻き粒子が 南方向へ飛んでいるという具合である。
そのような 単なる移動方向の違いが 本当に 上記で記したような 複雑で 人為的な違いを生じさせるのだろうか?
"スピン" は 移動方向に 性質が左右されるような 何かしらの未知な力を秘めているのだろうか?
Eq.70 を使って、 Eq.69 は、
(Eq.71)

右巻きスピノルの ウィークアイソスピンがゼロ (= Eq.70 ) は A と Z 粒子の統合に必要というわけである。
再び、次の新しい定義を行う。
(Eq.72)

これも単なるルールであり、明白な理由は何もない。
Eq.72 から、
(Eq.73)

また、次の新しい定義をする。
(Eq.74)
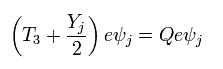
Eq.74 の Qe は フェルミ粒子の電荷を意味している。"Y" は ハイパチャージ である。
例えば、 uL の T3 と Y は それぞれ +1/2 と +1/3 である。 つまり アップクォークの電荷は、+2/3 となる。
uR の T3 と Y は、 それぞれ 0 と +4/3 である。 よって 右巻きの アップクォーク (R) の電荷も +2/3となる。
あなたがたは これらのルールが ちょっと人為的かつ 都合のよすぎると感じないだろうか?
Eq.72 と Eq.74 をつかって、Eq.71 の最初の項は、
(Eq.75)

お気づきのとおり、 Eq.75 は 光子とフェルミ粒子の相互作用項と同じである。 (Eq.17 を参照のこと。).
また Eq.72 と Eq.74 を使うと、Eq.71 の 2番目の項は、
(Eq.76)
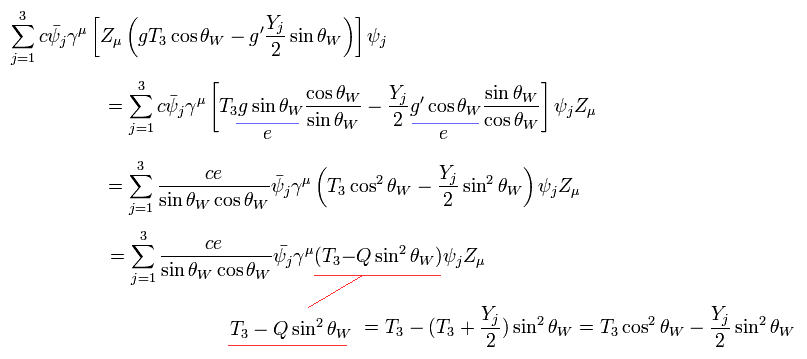
Eq.76 は Z ボゾンと フェルミ粒子の相互作用を意味している。
それらの結合力は 次のようになる。
(Eq.77)
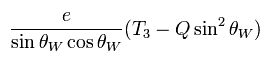
θw の角度は 様々な実験から 次のように決まっている。
(Eq.78)
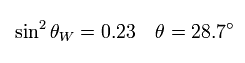
標準模型には 18 のパラメーター というものがあり、これらは この理論そのものから導くことはできず、実験から決めるしかない。
この 角度 θw、 結合定数 g と g' なども この 18 のパラメーターに含まれている。
もちろん、ヒッグス, W と Z ボソン、 レプトン、フェルミ粒子の質量はすべて これらのパラメーターであり、標準模型から導くことはできない。
( 上で述べたように これらの重要なパラメーターは 直接観測することができず、ただ それらの存在を推定するだけである。)
つまり 標準模型は 何も重要な値を予測できないということになる。
クライン・ゴルドン方程式のラグランジアンは、
(Eq.79)
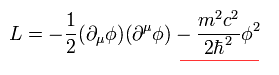
ここで 最初の項はエネルギーと運動量の項で 2番目の項は 質量項である。
重要な点は 質量項は ラグランジアンにおいて マイナス になるということである。 (つまりハミルトニアンではプラスになる。)
Eq.79 のラグランジアンは 次の変換で不変である。
(Eq.80)

次に 複素 クライン・ゴルドン場を考える。
複素場は (φ) は 次のように 2つの ( φ1 と φ2 ) からなる。
(Eq.81)
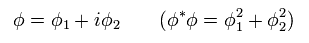
複素クライン・ゴルドン場のラグランジアンの1例は、
(Eq.82)

ここで μ と λ は実数である。
Eq.82 の2番目の項は プラス であるため、これは質量項ではない。
次の変換をしたとき、
(Eq.83)
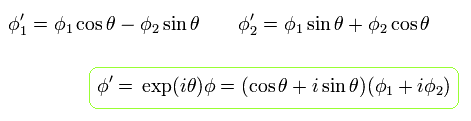
Eq.82 のラグランジアンは 不変である。Eq.83 は U(1) 変換である。
ハミルトニアンは ラグランジアンのマイナスにあたる。つまり Eq.82 の2、3番目の項は、
(Eq.84)
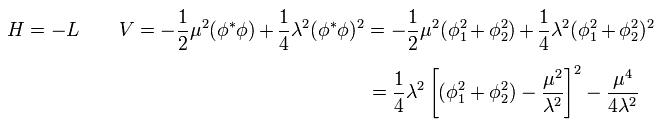
これらの項は 位置エネルギー V ( 質量項でなく ) を表す。
そのため 位置エネルギー Eq.84 は φ1 と φ2 が 次の関係を満たすとき、最も低くなる
(Eq.85)
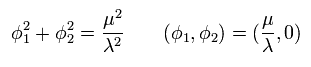
そのため、次の変数を定義すると、
(Eq.86)
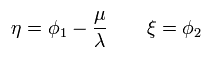
Eq.82 のラグランジアン ( Eq.84 の -V の項 ) は次のようになる。
(Eq.87)
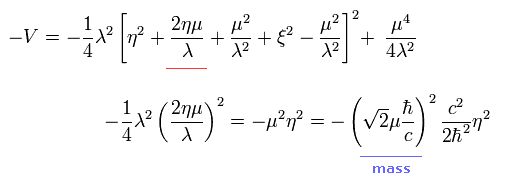
Eq.87 の 2番目の項は 質量項 を意味している。
しかし、そのかわりに Eq.87 のラグランジアンは対称でなくなる。
これは "自発的な対称性の破れ" と呼ばれ、”質量”を生じさせる。
しかし 残念ながら ここには まったく 明白なイメージ はない。
次に ローカルな SU(2) ゲージ変換を考える。
ここでは 次のように 複素クライン・ゴルドン場を定義する。
(Eq.88)

Eq.88 を使って、
(Eq.89)
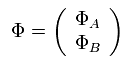
また ラグランジアンは、
(Eq.90)
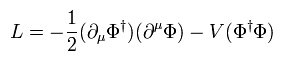
もちろん Eq.90 は 次の グローバルな SU(2) 変換で不変である。
(Eq.91)

次に Eq.90 のラグランジアンに Eq.92 の共変微分を使う。
(Eq.92)
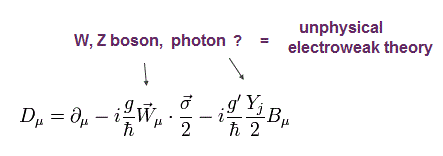
ここで 位置エネルギー V を 次のように定義する。
(Eq.93)
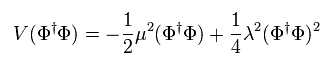
Eq.84 や Eq.85 のように、複素場が 次を満たすとき、位置エネルギーは最も低くなる。
(Eq.94)

ここでは Eq.88 と Eq.89 を使っている。
また 真空 を 次のように選ぶ。
(Eq.95)
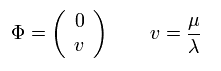
次のように 真空の電荷はゼロである。
(Eq.96)
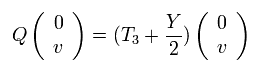
ここでは Eq.74 を使っている。
dL や eL (= Eq.96 の 2 × 1 行列 の2行目 ) の ウィークアイソスピンの第3成分は -1/2 である ( Eq.59 や Eq.60 を参照。 )
そのため、真空の ハイパーチャージ (Y) は、
(Eq.97)

実数場 h(x) を使って、 Φ を次のように再定義する。
(Eq.98)
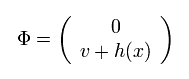
ここで h(x) は 有名な ヒッグス粒子 を意味している。
Eq.98 を Eq.93 ( Eq.84 を用いて ) に代入すると、 位置エネルギー V は、
(Eq.99)
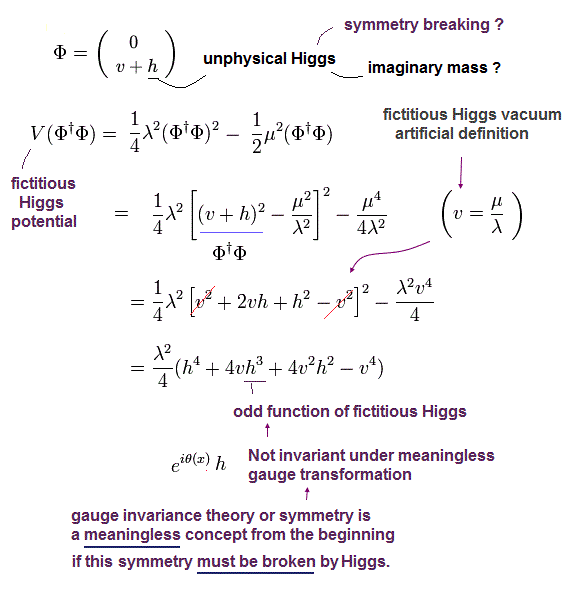
Eq.61, Eq.62 と Eq.65 (と Y=1 ) を使うと
(Eq.100)
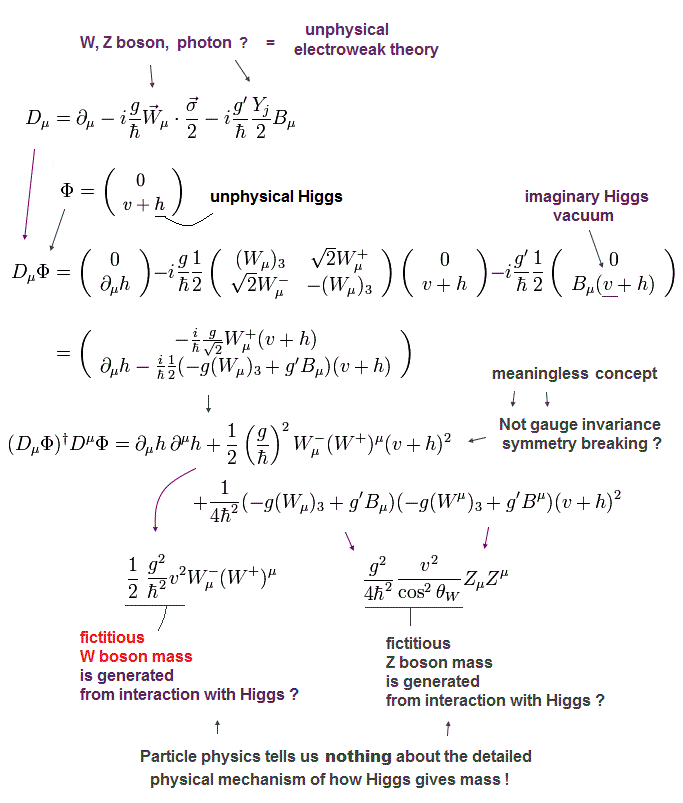
結果として
(Eq.101)
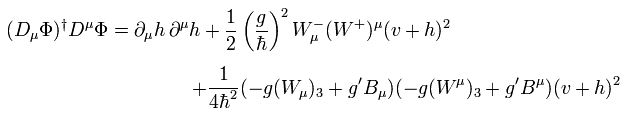
ここで (W-)* = W+ を使っている。
Eq.67 と Eq.73 から
(Eq.102)
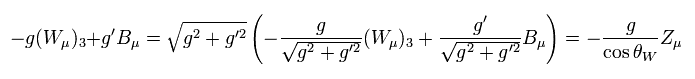
Eq.102 を使うと、 Eq.101 は
(Eq.103)
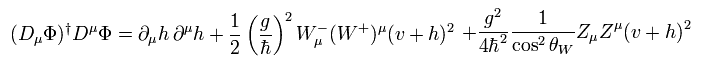
Eq.103 を ラグランジアン (Eq.90) に代入すると、次の項
(Eq.104)
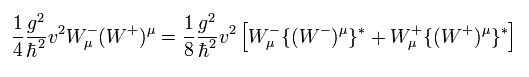
と 次の項
(Eq.105)
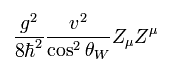
は重要である。 なぜなら これらの項は W± と Z ボソンの質量項を意味しているからである。
( Eq.90 のラグランジアンでは これらの質量項はマイナスである。)
結果として、Eq.98 の 自発的な対称性の破れは ウィークボソンに質量を生じさせたのである!
そして Eq.98 の h(x) は ヒッグス粒子を意味する!
これが ヒッグス粒子の正体である。
残念ながら、このヒッグス機構には まったく 具体的なイメージなるものが存在しない。
(あなたがたは どう思われただろうか?)
もし重いヒッグス粒子 (= 100 GeV 以上 )なるものが 本当に実在するとしたならば、私たちが この現実の世界で それらを感じることがまったくできないのはなぜなのだろうか??
( 標準模型によれば、ヒッグス粒子は 無数に存在しなければならない。)
また 加速器においては 何兆回もの衝突が 1つのヒッグス粒子を生じさせるのに必要とされている。
これほど低確率で曖昧な状態で 私たちは ヒッグス粒子をしっかり確認できたと本当に断言できるのだろうか?
次に クォーク と 強い力のグルーオンについて説明する。
クォークには 赤、青、緑の3色が存在すると言われている。
しかし クォーク は 単離できないため、観察される色は いつも 白ということになる。
( もし クォークが存在したらの話である。 )
そのため 波動関数は 次のように 12 × 1 行列 ( 最初は 3 × 1 行列とする ) となる。
(Eq.106)

ローカルな位相変換は、
(Eq.107)
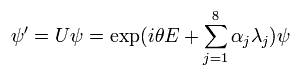
ここで λ は 次の8種類ある。
(Eq.108)

これらの λ 行列は 弱い力の パウリ行列に相当する。
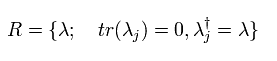
ユニタリ行列は 次のように エルミト行列から作ることができる。
(Eq.110)
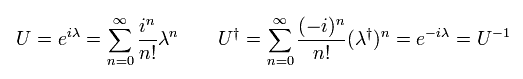
そのため Eq.107 の変換は ユニタリ行列となる。( これを SU(3) 群と呼ぶ。)
SU(3) バージョンの共変微分は、
(Eq.111)
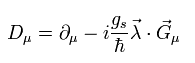
ここで G が "グルーオン" 場 を意味する。
Eq.111 の内積は 次の8つの項を含んでいる。
(Eq.112)
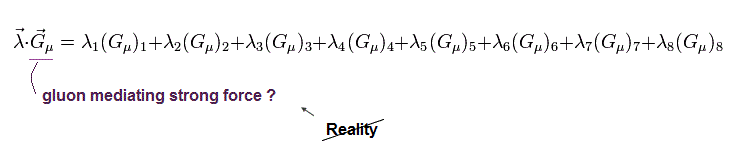
ラグランジアンがローカルな位相変換で不変のとき、次の関係式が満たされる。
(Eq.113)

Eq.111 を使って、
(Eq.114)
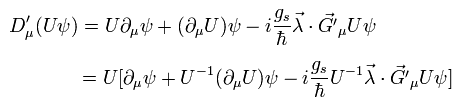
結果として、 Eq.113 は 次の関係式を満たす必要がある。
(Eq.115)
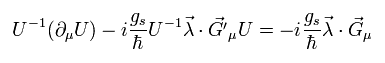
Eq.51-Eq.52'のように SU(3) の反対称成分は、
(Eq.116)
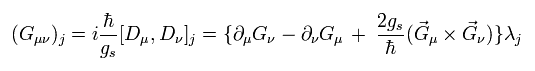
Eq.116 の外積は 次のように 8次元である。
(Eq.117)
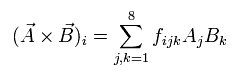
ここで f は、
(Eq.118)
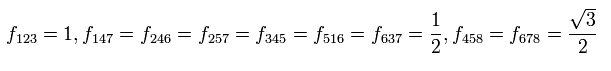
Eq.54 と Eq.55 のように Eq.116 の反対称成分を使うとき、 次の グルーオンのラグランジアンは SU(3) のゲージ変換で 不変になる。
(Eq.119)
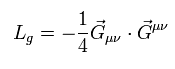
グルーオンは質量を持たないため、質量項の対称性を考慮する必要がない。
そのかわり、グルーオンの場合は 漸近的自由性という 非常に奇妙な概念を用いる。
しかし、この奇妙な性質なるものは本当に存在するのだろうか?
重要な点は クォーク自体は 分離して取り出せないということである。
そのため、これら クォークやグルーオンのリアリティーについて詳細に調べること自体が不可能である。
いわゆる "反粒子"は実在すると言われている。
しかし それらは 非常に不安定で それらのパートナーである "粒子" に出会うと 必ず消滅する。
はたして、そんな不安定な反粒子が本当に実在していると言えるのだろうか?
ここでは ベータプラス(β+)崩壊 と 電子捕獲 の違いについて述べる。
(Fig.14) どっちが起きる ?
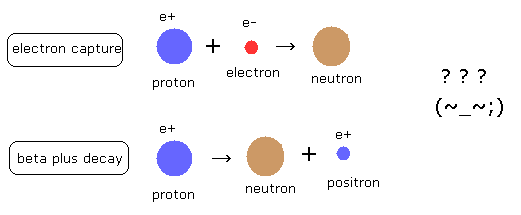
ベータプラス崩壊 (beta plus decay) と 電子捕獲 (electron capture) は 同じ原子核を生じさせる。
それらの両方とも、原子核内の 1つの陽子を 中性子に変化させる。
もちろん これらの反応は 原子核において 最終生成物が エネルギー的になりやすいときにのみ起こる。
結果、両反応とも エネルギーを放出する。
しかし はたしてそれらに違いなるものは存在するのだろうか?
(Fig.15) "どこで" エネルギーが放出されるのか ?
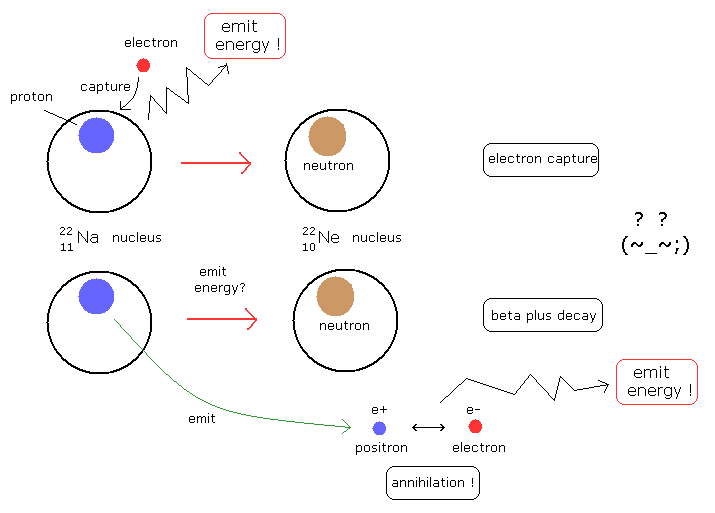
Na (22 11) は 電子捕獲と β+崩壊の両方が起きうるとされている。
電子捕獲では、原子核が 1つの電子を捕獲して 安定な原子核に変化したときに、エネルギーを放出する。
しかし、ベータプラス崩壊においては、原子核が 安定なものに変化しても まだエネルギーを放出しない。そのかわり 陽電子を放出する。
そして、陽電子が どこか別の場所で 電子に出会うと 両者は消滅して エネルギーを放出する。
つまり、これら2つの反応は 同じ原子核を生成するにも関わらず、エネルギーが放出される場所に関して 自己矛盾を含んでいることになる。
例えば、陽子が多い原子核で、最終産物と最初の産物のエネルギー差が 2mec2 以下だと β+崩壊は起こらず、電子捕獲のみ起こるとされる。
これらの反応は実は同じものなんじゃないだろうか?
( 陽電子と電子は 運動量をもつため、消滅エネルギーは 2mec2 より大きくなるのが普通である。)
もちろん、これらの原子核は 陽電子を放出した時点で、どこか別のところから飛んでくる電子の質量エネルギー のことまで あらかじめ予期しているわけではない。
結果的に 陽電子のからむ核反応は 電子捕獲のそれと完全に等しい。
例えば、ポジトロン断層撮影( PET )における核反応は Fig.14 に示すように 電子捕獲で置き換えることが可能だ。
( もともと βプラス崩壊では説明つかない現象が多々でてきたため、電子捕獲という概念が新たに取り入れられたのである。)
陽電子などの反粒子は非常に不安定で、かつ 反粒子からなる世界を今だに 私たちは見つけていない。
この現実の世界では、”粒子”のみが存在しており、私たちは粒子だけを必要としている。つまり 日々の生活に 反粒子はまったく不要な産物なのである。
まったく役に立っていない多くの種類の反粒子を実在すると考えること自体が不自然極まりない。
このページに示したように、陽電子は 高エネルギーの電子が 重金属にぶつかったときに生じる。理論的には 陽電子は 真空から生じることになっているのにも関わらずだ。
つまり、陽電子や 他の反粒子は 高エネルギーによって生じる 一時的な 励起状態のようなものではないだろうか?
加速器などにおいても、重金属が 陽電子の生成に使われている。
加速器内では たくさんの 光電子や 陽イオン が ノイズとして存在している。
また 各バンチ(塊)は 無数の生成された粒子で構成されている。
つまり、もう一度 非常に不安定な 反粒子の実在性について 再検証する必要があると、 私は思う。
標準模型における ほとんどすべての素粒子は とても不安定である。
ご存じのとおり、安定なものは 電子、陽子、電磁波、様々な原子核 (と ニュートリノ) しかない。
陽子は 電子に比べてかなり重い。しかし、それらの電荷の大きさは同じである ( +e, -e )。
つまり、陽子は 複合粒子でなんらかの小さなものから形成されていると考えるのは ごく自然である。
また、原子核は プラスに帯電しているにも関わらず 安定である。
つまり、中性子内の電子に加えて 何らかの強い力が 正の陽子同士を結合させていると考えるのも自然である。
問題は はたして クォークなるものは 実在するのか? ということである。
(Fig.16) "クォーク" は実在するのか ?

例えば、陽子は 2つの アップクォーク (+2/3e) と 1つの ダウンクォーク (-1/3e) からできているとされている。
しかし そのクォークの 各質量は たったの 3 (もしくは 6 ) MeV である。
陽子の質量は なんと 938 MeV である。
つまり、陽子の質量のほとんどは グルーオンの関係する強い力のエネルギーなどによるとされている。
( もちろん、私たちは 色のせいで クォーク1つを単離することはできないので 直接これらを確認するのは不可能である。)
それに あなたがたは +2/3e や -1/3e などの分数電荷がちょっとできすぎていると思わないだろうか?
このページ や このページ に示したように、散乱断面積は 各粒子の電荷に比例する。
クォークは1つでは観測することはできない。
それは 他のクォーク (もしくは 反クォーク) と結合して より 安定なものへ崩壊する。それは "ジェット" として観察される。
最終産物の 電子、γ線、ニュートリノなどのエネルギーから、様々な 不安定な粒子の質量を推定するのである。
( しかし 肝心な ニュートリノ のエネルギーが 完全に測定することができない。)
近似的に、クォークのペアの生成は 他のハドロンの生成に似ているとする。
アップ (+2/3e), ダウン (-1/3e), ストレンジ (-1/3e), チャーム (+2/3e) の生成と 3つのカラー (赤、青、緑) ができると推定して、断面積は 次に比例するとする。
(Eq.120)
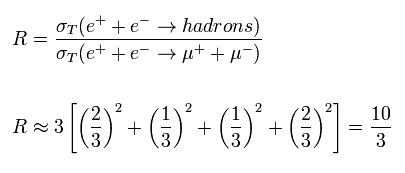
あるエネルギー範囲においては、R が だいたい 10/3 付近になることがある。
他のエネルギー範囲においては、他の粒子が生成されるとされている。
しかし これらは 単なる推測にすぎない。
例えば、私たちは 上の 4つのクォークが実際に 生じているのか知ることができない。
それに とても強いグルーオンと 電荷との関係はどうなっているのだろうか? 要するにそんな単純な話ではないと思われる。
また、それらのクォークと3つの色の生成が同確率で起こるという証拠があるわけでもない。
また 無数のノイズのせいで これら粒子が生成される確率は 実に 何兆回の衝突につき 1つである。
さらに 最終生成物の解釈は 現在の標準模型が正しいことを前提条件としている。
もし、私たちが QED (量子電磁気学) や QCD (量子色力学) などを忘れれば、もっと リアリティーのある素粒子 が きっと見つかると私は思う。
ミュー粒子は その電荷がマイナス (-e) で 電子の質量の 約200倍の重さの 素粒子である。
また ミュー粒子の平均寿命は 約 2.2 μs ( 2.2 マイクロ秒 ) で、すぐに 電子とニュートリノ に崩壊する。
このように ミュー粒子がすぐに 電子とニュートリノに崩壊するのに それを素粒子と呼んでいいのだろうか ??
ミュー粒子を 電子と 高エネルギーのド・ブロイ波 の混合物と考えるのがより自然である。
(上で述べたように、地球を通り抜けるニュートリノを "残りの ド・ブロイ エネルギー波" と見なすのが自然である。)
また、電子のエネルギーが大きくなる (= そのド・ブロイ波が短く かつ その波の速度が 光速cに近づく) につれて、最高速度がcである 電場によって それを加速することが難しくなってくる。
つまり、媒質の理論を用いて 自然に 相対論的な質量変化を説明することができる。
よって この 電子の重い相対論的質量なるものによって 霧箱中の 電子の約 200 倍 の重い質量の運動を説明することができる。
もしくは 高エネルギーのドブロイ波に絡まった状態で 電子は 一時的に通常と違った質量の性質を示す可能性もある。
ここで 非常に興味深く かつ 感銘を受けた本の1つを紹介する。
------------------------------------------------------------------------
リー・スモーリン
迷走する物理学。ストリング理論の栄光と挫折、新たなる道を求めて。
-------------------------------------------------------------------------
この本は 現在当然のごとく受けいれられている 相対論と量子論などの基本的な物理学に 実は 重大な欠陥があると示唆している。
彼は 量子力学と場の量子論の リアリティーの欠如 についても言及している。
また この本によれば、現在の理論物理学は ”人為的に”数学を操作したり、余剰次元のような 非現実の世界を取り入れて 無理やり実験結果にあわせようとしている と言っている。
もちろん この作者は 素粒子物理学、理論物理学の経験豊富な エキスパートであり、現在の物理学の状況を 客観的かつ的確に分かりやすくのべている。
ぜひ みなさんに読んでいただきたい本の1つである。
ここで 例として 時間並進を計算してみる。
このホームページの QED の表記法や関係式については、 このページ と このページの Ap.1 を参照のこと。
また 基本的な QFT に関するこのページをまだ読んでいなければ、先に読んでほしい。
無限小座標変換が次で表されるとき、
(Eq.3)
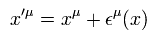
作用 S の変化は、
(Eq.4)
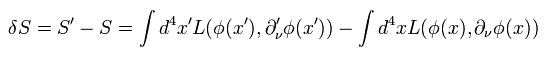
もちろん、この S は 相対論のもとでは 不変でなければならない。
φ などの 場の変数の変換と違って、時間と空間の変数 (= x, t ) そのものの変換のときは、d4x の変化も考慮する必要がる。
(Eq.5)

ここで Eq.3 を用い、行列式の計算のとき 2次の無限小を省略した。
Eq.3 の変換のもとで、ラグランジアン (L) の変化量は
(Eq.6)
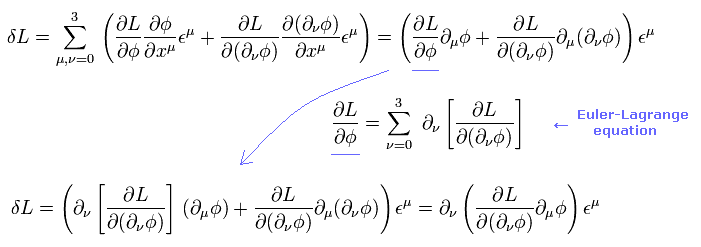
ここでは このページ (Eq,1-17') のオイラー・ラグランジュ方程式を用いた。
よって Eq.4 の 作用 S' は、
(Eq.7)

ここでは 部分積分を使用した。
Eq.7 の ストレスエネルギーテンソルの (0,0) 成分は、 ディラックのラグランジアンを用いると、
(Eq.8)

この結果は このページ (Eq.5-39)と同じである。
このように 相対論的な場の量子論では ハミルトニアンは 時間平行移動のもとで 保存される。
彼らはこの類似性をゲージ不変性にも 応用したのである。

2011/12/29 updated This site is link free.