量子電磁力学 (QED) の終わり。

トップページ (２正確な新ボーア模型)
異常磁気能率計算のトリック。
特殊相対論は間違っている。
様々な場における伝播関数。

目次 (13/1/25)

• QED が間違っている理由。
• "仮想光子" が アインシュタインの質量公式を満たす。＝ QED のトリック。
• 量子電磁力学とファインマン則。
• QED における 様々な数学的なトリック。
• 異常磁気能率と磁場における矛盾。

QED が間違っている理由。

[ 量子電磁力学は 物理でなく 単なる "間違った数学" である。 ]

(Fig.1) 間違った数学？

あなたがたは 量子電磁力学 (QED) は 世界で最も成功した理論であり、異常磁気能率 (= ｇ因子 ) や ラムシフトなどの正確な値を予測できると聞いたことがあるかもしれない。
しかし実際は QED は 間違った 人為的な数学のトリックを使っており、また 物理的なイメージがまったくないことを示す。
( 実際に あなたがたが 長い期間をかけて QED について勉強しても、QED は 実社会でまったく役に立たない。)

QED が誕生してから 半世紀以上が経過したにも関わらず、今だに 繰り込みに基づく QED の数式がどうして正確な値をだすのかという 基本的な理由が不明のままなのである。
繰り込みとは 非常に小さな値をだすために 無限大を人為的に除去するという意味である。

(Fig.2) ”無限”の裸の電荷と質量はリアルなのか？

QED によれば、電子の裸の電荷と質量は 無限大でなければならない。（ あなたがたは これがリアルだと思われるだろうか？ ）
なぜなら 無限大の数値が 人為的に 電子の電荷と質量に 詰め込まれるからである。
つまり、この QED には 非常に多くの反対意見が存在する。
例えば、ファインマン自身、彼の本のなかで 繰りこみに関して "shell game" (トリック)、 "hocus pocus" (ごまかし) などと述べている。

さらに 「ディラック現代物理学講義 」によれば、ディラックは QED の繰り込み手法に非常に不信感を持っていたらしい。
( 量子の海、ディラックの深淵、グレアム・ファーメロ著 も参照のこと。)
ディラックは 数学のエキスパートだった。
そのため 非常に小さな値を無視することは 妥当だが、無限大を無視することは理解できない と言っている。
( QED の手法は 完全に ディラック方程式に依存しているにも関わらずだ。)

(Fig.3) 特殊相対論の致命的な欠陥 = QED は間違い。

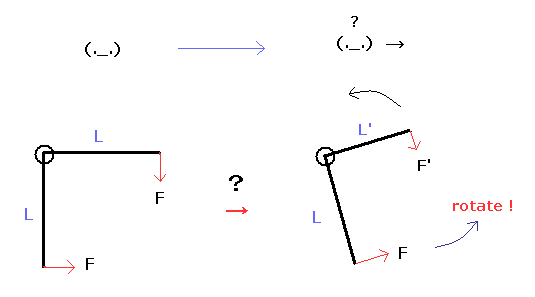
このページに示したように、様々な致命的なパラドックスは 特殊相対論が間違いであることを示している。
（ たった１つでもパラドックスがあれば、その理論が間違いであることを意味するが、実際 いろんなパラドックスが存在する。）
もちろん、特殊相対論が間違いであれば、QED も 間違いである。なぜなら QED は ディラック方程式を通じて 相対論的な エネルギーと運動量に完全に依存しているからである。
このページに示したように、ディラック方程式は 特殊相対論そのものである。

無限大を人為的に取り除くトリックに加えて 特殊相対論が間違いであれば ダブルパンチで QED が間違いであることの証になる。

[ 古典的なローレンツ力 + ディラック方程式 = QED. ]

(Fig.4) ローレンツ力 → ファインマンダイアグラム。

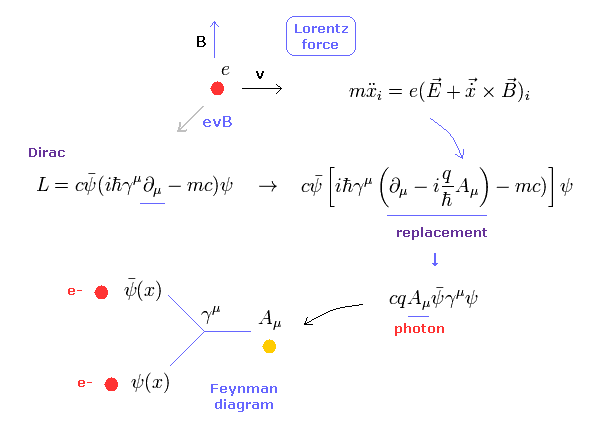
このページに示したように、QED における 電子と光子間の相互作用は 古典的なローレンツ力に起因している。
QED では、光子は 磁気と電気ポテンシャル (= A, φ ) で表される。
ディラックのラグランジアンで 演算子の置きかえをすれば、ファインマンダイアグラムを与える 相互作用項を得ることができる。

また この相互作用の形式が QED における 電子と光子の 唯一の相互作用となる。
つまり "数学上の" QED には 何の物理的なイメージがないことを覚えておく必要がある。

(Fig.5) 相互作用ハミルトニアンにおける 時間発展。

このページに示したように、場の量子論は 電子 (= c ) や 光子 (= a ) などの粒子を 非常に抽象的な 生成消滅演算子としてしか表現できない。
Fig.4 の相互作用項を用いると、電子と光子の相互作用を表す 相互作用ハミルトニアン (= H_I ) を得ることができる。

場の量子論では、時間発展を 指数関数＋ハミルトニアンで表現する。
この指数関数を展開すると、様々な数のハミルトニアンから成る項を得ることができる。
ｇ因子補正に関するこのページでは、３つのハミルトニアンから成る項を使用する。これは無限大に発散する。

(Fig.6) ファインマンダイアグラム -- ３つのハミルトニアン (= 頂点 )。

Fig.6 は ３つの相互作用ハミルトニアンのケースを示している。
運動量 " p " を持つ "in" の電子と 運動量 " q " を持つ光子は 融合して "out" の電子 " p' " になる。
エネルギーと運動量は p' = p + q で 保存される。
各頂点は １光子 (= A、茶色 ) と ２フェルミ粒子 (= ψ、 青 ) で構成される。

２つの同種類の粒子 ( 光子 - 光子 もしくは 電子 - 電子 ) を繋げると、ファインマンダイアグラムを得ることができる。
Fig.6 の ３つの内線は ( 光子もしくはフェルミ粒子の ) 伝播関数 ( propagator ) と呼ばれる。

(Fig.7) 繰り込み = 無限の裸の電荷。

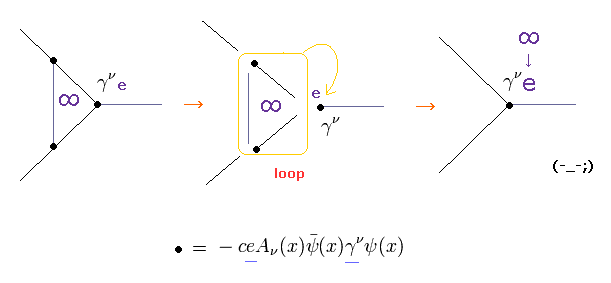
後で説明するが、Fig.6 は １つのループと３つの内線 (= 伝播関数 ) から成り立っている。
ローレンツ変換不変にするには、各波動関数は 無限種類の運動量とエネルギーを含まなければならない。
そのため この時間発展のループは 無限大に発散する。

QED では、この無限大の値を 電子の 非常に小さな電荷 "e" に 人為的に詰め込む必要がある。
結果的に、非常に小さな電子の電荷 "e" は 無限大になってしまう。
この相互作用の形式自体は これらの操作によって保たれるため、彼らはこの手法に満足しているのである。
( あなたがたは どう思われるだろうか？ )

[ QED の ｇ因子は ”間違った”数学に基づいている。 ]

(Fig.8) 変数変換 = QED のトリック。

Fig.8 の上部の式は k² の項のみ含んでおり、ｇ因子の情報を含んでいない。
それを 変数 "k" に関して積分すると、それは無限大に発散する。
なぜなら 積分範囲は -∞ から +∞ だからである。

積分変数を k → l - β のように変更すると 、新たな β の項が出現し、この β が ｇ因子の情報を含んでいる。
単一の " l " の項は 積分でゼロになる。なぜなら それは奇関数だからである。

l² の項は無限大に発散するが、この項は 繰り込みによって 人為的に除去する。
結果的に ｇ因子の値が得られるというわけである。このページで詳しく説明した。

(Fig.9) 無限大は無限大のまま ( 有限値でなく ) 。

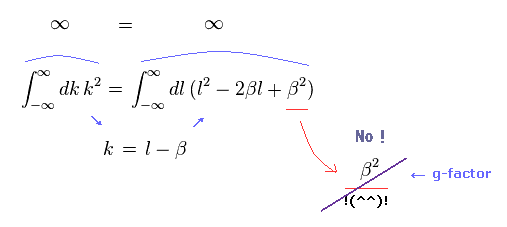
もちろん、ｇ因子の計算に使用されている Fig.8 の方法は間違いである。
元の k² の積分は ( l² -2βl + β² ) の式全体に等しい。 よって ∞ = ∞ が満足されている。
有限の β² の項は 無限大の中でゼロになってしまう。
ここで 有限の β の値のみ取り出すことは 通常の数学によれば 許されない。
つまり この方法は 間違った数学なのである。

この間違った数学を用いて、もともと ｇ因子を含んでいなかった項に ｇ因子の情報を容易に追加することができる。

(Fig.10) QED は 無限大を利用している。

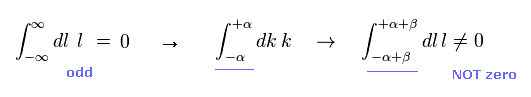
QED の計算では、マイナス無限大から プラス無限大に積分することによって、奇関数 " l " を消去することができる。
もし もともとの積分範囲が 有限な範囲だとしたら ( -α から + α )、 単一の " l " を含んだ項を 消去することができない。
なぜなら 積分変数の置換によって 奇関数 " l " を与えることができないからである。

もちろん、これらの項を消去できなければ、ｇ因子の値を得ることはできない。
つまり QED は 無限大を利用するだけ利用して 後で 人為的にそれを除去しているのである。

[ QED の間違った数学 パート II。 ]

(Fig.10') この数学は正しいのか？

Fig.10' の上では、"k" は奇関数のため 積分するとゼロになる。
積分変数を変換すると ( k = l - β )、" l " の項が 奇関数のため 積分でゼロになる。
結果的に "-β" の部分のみ残り、ここに ｇ因子の情報が含まれていることになる。
この数学的手法は QED の ｇ因子の値を得るのに 必要不可欠なものであるが、あたながたは Fig.10' の数学が正しいものだと思われるだろうか？

(Fig.10'') 正しい数学。

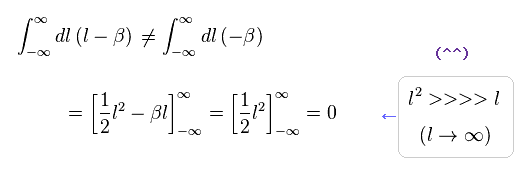
Fig.10'' は 正しい数学を用いたものである。この正しい数学によれば、もちろん "-β" の項もゼロになることはいうまでもない。
なぜなら、それらを積分すると、 " l² " の項が " βl " の項の部分よりも はるかに早く発散するからである。
結果的に " l² " の項のみ残り、この結果はゼロになる。
( 正しい数学によれば、 "β" の部分は "l" の項に吸収されてなくなってしまう。 )
つまり Fig.10' の QED の数学的手法は 数学の基本を破っているのである。
実際の例に関しては このページを参照のこと。

"仮想光子" が アインシュタインの質量公式を満たす。＝ QED のトリック。

[ 仮想光子は QED に必ず現れる。 ]

このセクションでは、Fig.6 の 光子 "q" は 相対論に違反する 仮想光子であることを示す。
これらの タキオン様の仮想光子は QED、ゲージ理論、標準模型に 特異的なものである。それらが相対論的な理論にも関わらずだ。
静止した １つの電子 (= p ) が １つの光子 (= q ) を吸収して p' の電子になるとする。
(Fig.11)

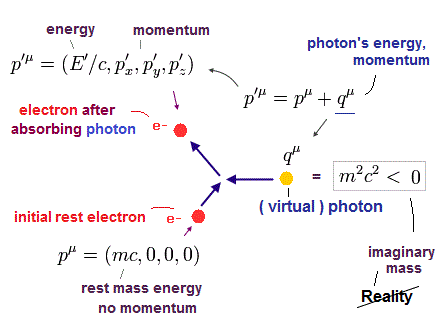
静止した電子 (= p ) のエネルギーは 静止質量エネルギー ( E/c = mc ) のみである。
光子を吸収したあとの電子 (= p' ) には運動量がある。
光子と相互作用する前と後の電子は アインシュタインのエネルギーと運動量の関係式を満足する必要がある。
(Eq.1)

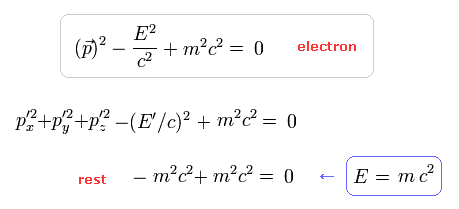
Fig.11 と エネルギー・運動量の保存より、光子のエネルギーと運動量は
(Eq.2)

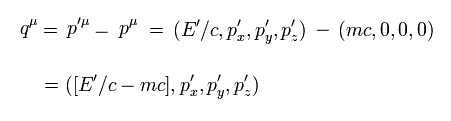
ご存じのとおり、光子の質量はゼロである。しかし Eq.1 と Eq.2 より、
(Eq.3)

Eq.3 は この光子の質量は 虚数であることを意味している。
なぜなら Eq.3 のエネルギー・運動量の関係式は リアルな粒子においては ゼロもしくは ゼロ以下になる必要があるからである。
(Eq.4)

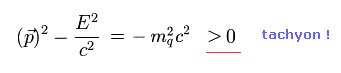
つまり Eq.3 は この光子が 相対論に反する タキオンであることを示している。
Fig.6 に示すように、このタキオン様の光子 "q" は ｇ因子の計算において 主要な役割を果たしているのである。
( つまり 相対論的な QED は 最初から 自己矛盾を含んでいることになる。 )

[ ディラック方程式における アインシュタインの質量公式。 ]

このセクションでは、この仮想光子 "q" が ｇ因子において ゼロになることを示す。
( 通常の QED の教科書は この重要な事実を明確に書いていないが・・・。)
もし この仮想光子がゼロ ( q = 0 ) ならば、 "out" の電子 " p' " の運動量などは "in" の電子 " p " とちょうど等しくなる。
( p' = p + q, ← q = 0. )
結果的に、ｇ因子 ( 異常磁気モーメント ) は いかなる値もとることが可能になる。
これはつまり、私たちの自然界は QED を通して たった１つのｇ因子を決めているわけではないということになる。
( つまり QED は 真の理論ではないのである。)

(Eq.5) ディラックの関係式 = アインシュタインの質量公式。

このページに示したように、ディラック方程式は 相対論的なエネルギーと運動量の関係式に起因している。
( このページでは、 (-1,1,1,1) バージョンの計量テンソルと使用している。 このページも参照のこと。 )
つまり Eq.5 のディラックの関係式の意味は p² - E²/c² + m²c² = 0 のアインシュタインの関係式と同じ意味である。
Eq.1 のように、 Eq.5 を用いるとき、"in" と "out" の電子は アインシュタインのエネルギーと運動量の関係式を満足する。
結果的に 光子 "q" は 仮想光子 ( ← p' = p + q. ) になる。

(Eq.6) QED ｇ因子の計算。

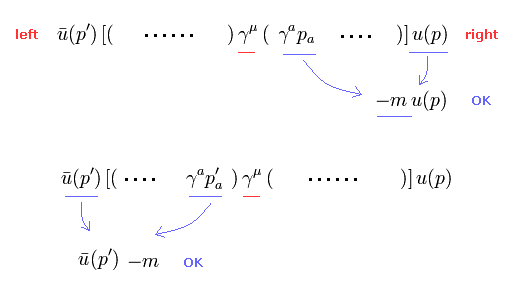
後で説明するが、１ループの伝播関数は Eq.6 のような形式を与える。
Eq.6 では p' は γ^μ の 左側にあり、 p は 右側にある。
Eq.5 の質量の関係式を用いると、 右側のγ^ap_a を- mに、左側 の γ^ap'_a を -m に変化させることができる。

[ p と p' を γ^μ の別サイドに移動すると ｇ因子を生じる。 ]

つまり γ^μ の左側の p は -m に変化させることはできない。
なぜなら p は p' と 異なるからである。
同様に γ^μ の右側の p' も -m に変化させることはできない。

(Eq.7) p と p' の違い。

もちろん、p と p' の違いは 仮想光子 q の存在によるものである。
そのため この仮想光子 q が ゼロでないときのみ、 Eq.6 のルールは有効になる。
( この事実を心に とめておくように。)
(Eq.8)

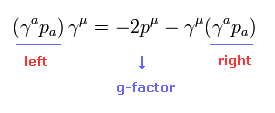
ｇ因子の計算では、p もしくは p' を γ^μ の １サイドから 別のサイドに移動する際に Eq.8 の関係式を頻繁に使用する。
この操作のために、 γ^μ を含んでいない新たな項が出現する。
彼らの理論によれば、この新たな項が ｇ因子を表している。

もちろん、これらは 彼らが QED のｇ因子を最初に計算した際に導入した 単なるルールにすぎない。
つまり どうして 左側の "p" をそのまま繰り込みしていけないのかという明確な理由は何もない。

(Eq.9) 左側の "p" を 右側に移動。

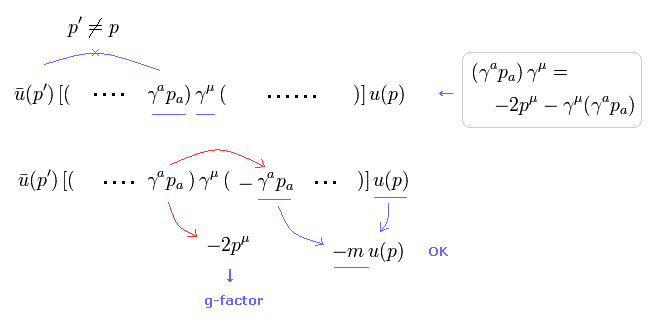
仮想光子 q がゼロでないとき、p は p' と等しくない ( p' = p + q )。
そのため、左側の "p" は Eq.5 を用いて "-m" に変更できない。
このケースでは Eq.8 を用いて "p" を右サイドに移動して -m に変更しなければならない。
この過程で、ｇ因子の一部が 生成される (= -2p^μ ).

(Eq.10) 右サイドの p' の 左サイドへの移動。

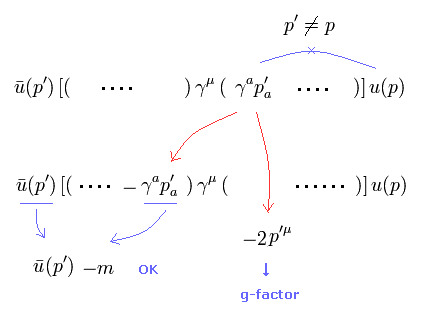
Eq.10 では、 p' は 右サイドにあるため、Eq.5 を用いて -m に変更できない。
そのため、p' を左サイドに移動させて -m に変更させる必要がある。
この過程でも ｇ因子の一部が生成される。

(Eq.11) 仮想光子 q = 0 → ｇ因子は自由に操作できる。

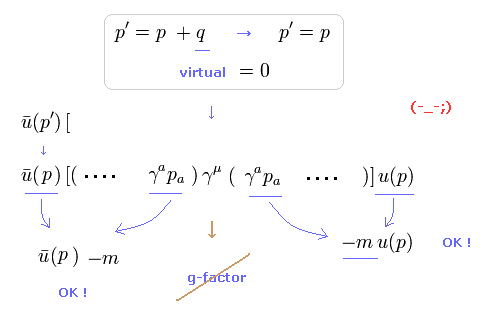
この仮想光子 q がゼロのとき、 p と p' の違いは消失する。
結果的に p' は p になるため、私達は p (= p' ) を "-m" にするため わざわざ他サイドへ移動させる必要がなくなる。
もちろん、ｇ因子を生成させるために それらを他サイドへ移動させることも可能である。
これはつまり 仮想光子 q がゼロのとき、QED のｇ因子は いかなる値も取り得ることを意味している。

驚くべきことに QED の手法では ｇ因子を得るために この仮想光子をゼロにしているのである。
つまり QED の精密な計算の 真のメカニズムについて 私達が問うとするならば、この手法は 単一の値を決定するということに関して 間違っているということになる。
私達の自然界の法則は ｇ因子の決定のために この QED を採用していないのである。 ( ｇ因子は操作できるのページも参照のこと。 )

[ ｇ因子を得るためには 仮想光子はゼロになる必要がある。 ]

(Eq.12) ｇ因子を得るために q² = 0 は必要不可欠である。

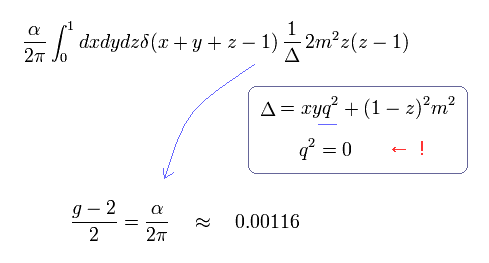
後で説明するが、ｇ因子を得るためには q² = 0 の条件は 必要不可欠である。
q² の表記は 次のように アインシュタインのエネルギー・運動量の関係式を表している。

(Eq.13) q² = アインシュタインの関係式。

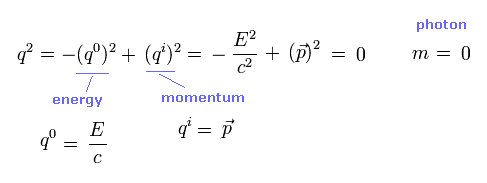
このページでは、 (-1,1,1,1) バージョンの計量テンソルを使用している。 ( このページも参照のこと。 ).
光子の質量はゼロのため、Eq.13 のアインシュタインの関係式は 正しいように見える。
しかし この光子 q は 特殊相対論に矛盾する 仮想光子であることを思い起こす必要がある。

[ 仮想光子 + 特殊相対論 → 光子のエネルギー q は ゼロ。 ]

(Fig.12) 仮想光子 + 相対論 = エネルギーゼロ。

この仮想光子が 特殊相対論に従うとき、そのエネルギーと運動量は 完全にゼロになる。
次に この事実を証明することにする。

(Fig.13) p' = p + q.

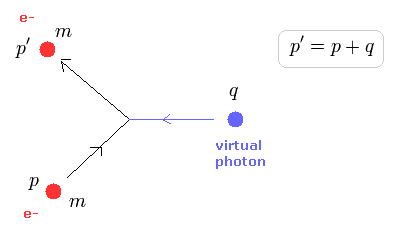
Fig.13 の "in" と "out" の電子は アインシュタインの公式を満たす。
(Eq.14)

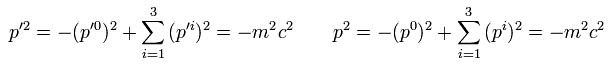
そのため、
(Eq.15)

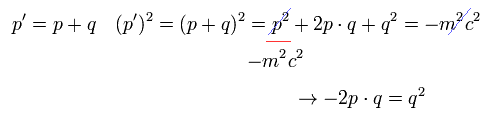
Eq.15 から、 q² = 0 (= 光子の質量ゼロ ) を仮定すると、
(Eq.16)

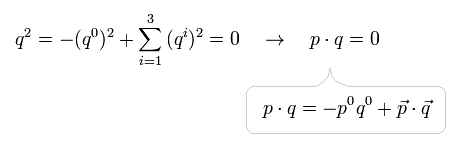
ここで "pq" も アインシュタインの公式を意味する。

ある方向では "in" の電子と光子のエネルギーと運動量は
(Eq.17)

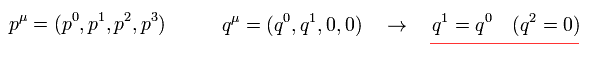
ここでは ゼロ成分は エネルギーで 他の成分は運動量を意味している。

Eq.16 と Eq.17 から、次のように q=0 を得る。
(Eq.18)

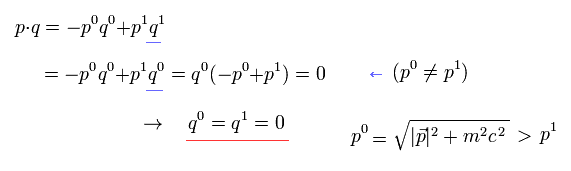
電子の質量エネルギーのために、 p⁰ は p¹ よりも必ず大きい。

結論として "in" と "out" の電子 (= p と p' ) が アインシュタインの質量公式を満足する、エネルギー・運動量の保存 ( p' = p + q )、 仮想光子 (= q ) が アインシュタインの質量公式を満たす ( q² = 0 ) の ３つの条件を満足すると 仮想光子 ( q = 0 ) のエネルギーはゼロになる。
( 仮想光子のすべての成分 0-3 が ゼロになる。 )
この非常にゆるい条件の中で、QED の計算は あらゆるｇ因子の値を得ることができる。

[ 様々な人為的なルールも QED のトリックの１つである。 ]

(Fig.14) 様々なルール。

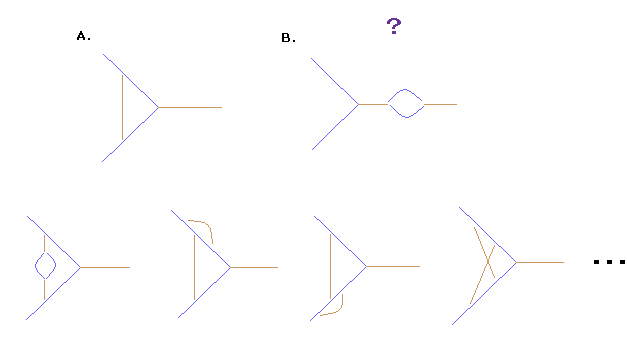
３つの頂点のｇ因子の補正において、Fig.14A のパターンのみ使用した。
そして Fig.14B のパターンを 無視した。これも ３頂点で１ループにも関わらずだ。
もし Fig.14B も考慮すると、 ｇ因子の値は 元の約２倍になる。もちろん このケースは間違いである。
Fig.14B のパターンを無視することも QED における 人為的なルールの１つである。

もっと高次の補正では、もっと多くの積分変数や 他の変数 ( p、 p'、q ) を操作することができる。
また 違った種類の自己エネルギーのパターンも出現したりして ｇ因子を得るための いくつかのファインマンダイアグラムを選ぶことができる。
ラムシフトの計算においても、実験値を得るための 他の様々な ルールが導入された。
しかし QED のラムシフトも 上記の頂点補正を一部として含んでいるため、仮想光子がゼロのとき QED のラムシフトの値も決まらないことになる。

[ 量子電磁力学 (QED) は 本当に正確なのか？ ]

(Fig.15) QED = 無限大。

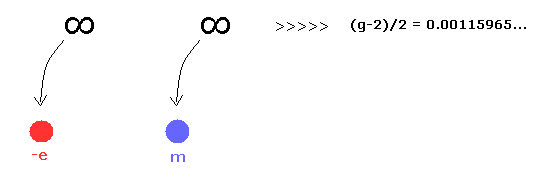
量子電磁力学 は 電子のｇ因子 (異常磁気モーメント) や ラムシフト などの 非常に正確な値を得ることができると言われている。
しかし 実際には 正確な値とは かけ離れた 無限大の数を与える。
そのため 量子電磁力学 (QED) によれば、電子の 裸の 電荷と質量は 無限大ということになる。
"自然界" は 果たして本当に QED の無限大のルールに従っているのだろうか？？

ここでは 電子のｇ因子 ( g-2 ) の計算において、QED の様々な 数学的なトリック について説明する。

最近の興味深い報告によれば、微細構造定数 α が 変化しているらしい。
( J. K. Webb, et.al. Phys. Rev. Lett. 107, 191101 (2011) )
また 最近の NIST の チタンイオンを用いた興味深い実験によれば QED の予測と一致しなかったらしい。
( C. T. Chantler, et.al. Phys. Rev. Lett. 109, 153001 (2012) )
もし これらの結果が本当なら、QED の信頼性 が失われることになる。

量子電磁力学とファインマン則。

[ 様々な場における ファインマン伝播関数 ( スカラー、ディラック )。 ]

(Fig.16) 内線 = 伝播関数。

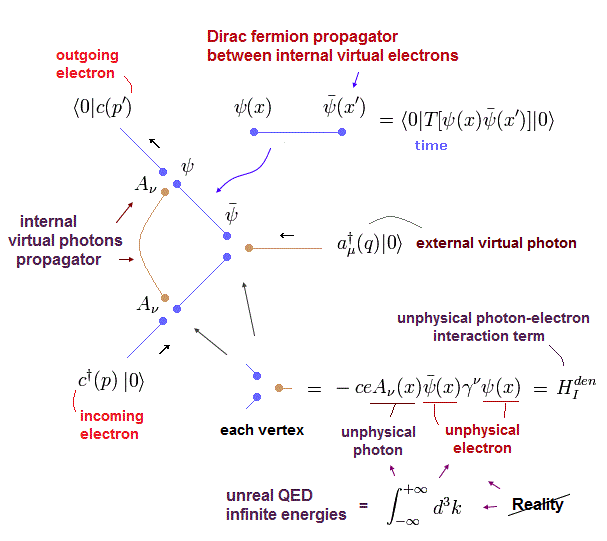
伝播関数は 量子電磁力学における様々な値を計算するための基本的なツールである。
そのため このセクションでは、様々な場 ( スカラー、ディラック、電磁場 ) におけるファインマンの伝播関数について説明する。
伝播関数について理解するには、最初に 基本的な場の量子論について理解する必要がある。
そのため もし読んでいなければ このページを先に読まれるように。

(Eq.19) ディラックの伝播関数 (= 電子 )。

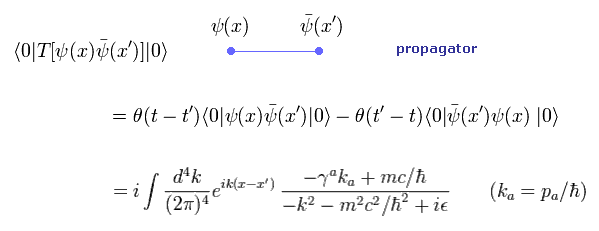
(Eq.20) 光子の伝播関数。

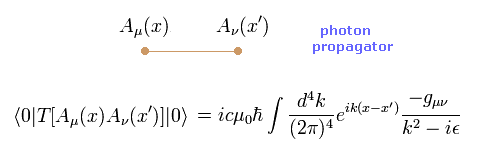
Eq.19 は ディラックの伝播関数 ( 電子 - 電子 ）で、 Eq.20 は 光子の伝播関数である。
伝播関数は Fig.16 のファインマンの伝播関数の内線であり、時間発展は 階段関数 θ を用いて表される。
詳細な計算に関しては、スカラー、ディラック、光子のプロパゲーター のページを参照のこと。

[ QED における １頂点、ループなしのダイアグラム。 ]

このページに示したように、電子と電磁場の間の 相互作用ハミルトニアンは、
(Eq.21)

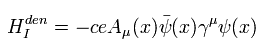
ここでは 基礎的な場の量子論のルールにより、 A_μ γ^μ は すべての成分 (μ = 0, 1, 2, 3) に関して足し合わせる必要がある。

ハミルトニアン (= H_I ) は ハミルトニアン密度の空間積分から得られる。
(Eq.22)

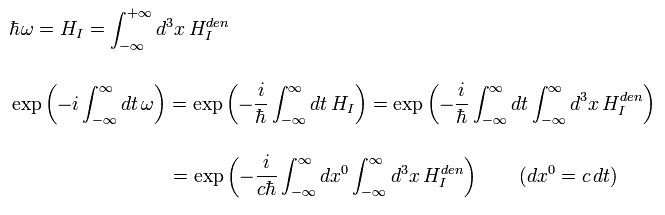
ここで Eq.22 の指数関数部分を 次のように テイラー展開する。
(Eq.23)

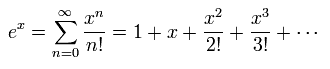
Eq.23 を用いると、 Eq.22 は 次のように表せる。
(Eq.24)

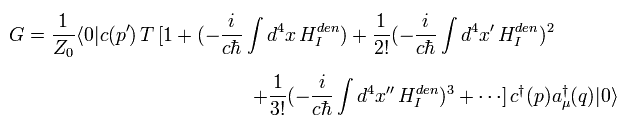
ここで c^†(p) と a^†(q) は 頂点に入っていく 外電子と 仮想光子を意味している。
そして c(p') は 頂点を 去る 外電子を意味している。
( p、 q、 p' は 各粒子の運動量とエネルギーである。)
ここで p + q → p'.
時間発展や QED における ハイゼンベルグ、相互作用表示に関しては このページを参照のこと。

最初に Eq.24 (Fig.17) において １次のハミルトニアン密度について計算する。
( １次とは Eq.24 の２番目の項のことである。 )

(Fig.17) １ハミルトニアン。

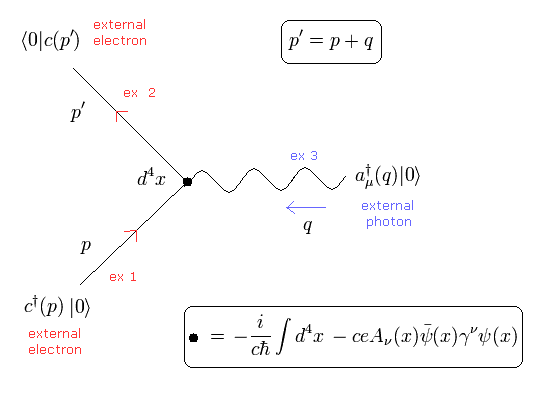
Fig.17 は 内線 (= 伝播関数 ) と ループ を含んでいない。
Fig.17 の ファインマンダイアグラムは、
(Eq.25)

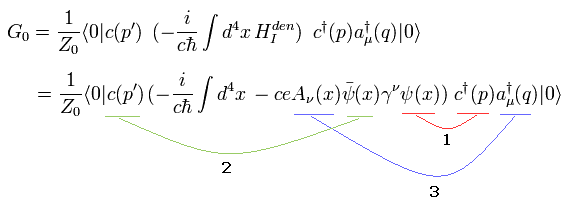
Eq.25 に示したように、２つの同種類の演算子 ( 電子-電子、光子-光子 ) が繋がっている。
このページに示したように、ディラックの解は、
(Eq.26)

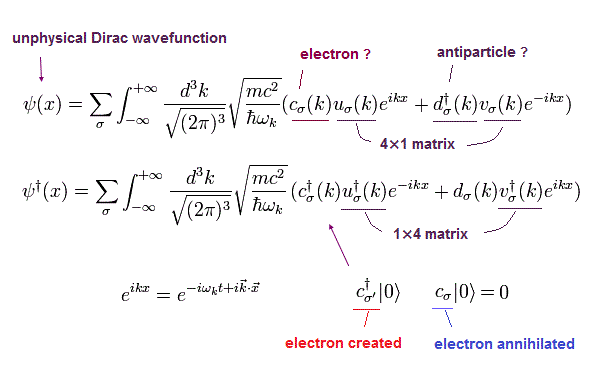
ここで c は 次の反交換を満たす。
(Eq.27)

Eq.26 と Eq.27 を用いると、Fig.17 と Eq.25 の外線 1 ( 電子-頂点 ) は、
(Eq.28)

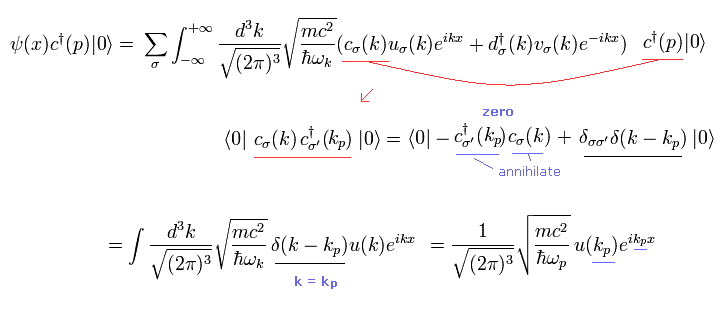
ここで k_p は 電子１の 波数 = p / ħ を意味している。
" c^†c " は 両サイドの真空によって消える。

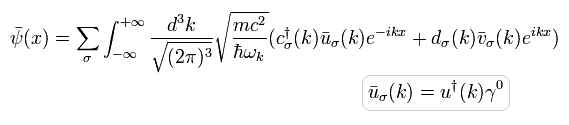
同様に、 Eq.27 と Eq.29 を用いると、 Fig.17 と Eq.25 の外線 2 (頂点を去る電子 ) は、
(Eq.30)

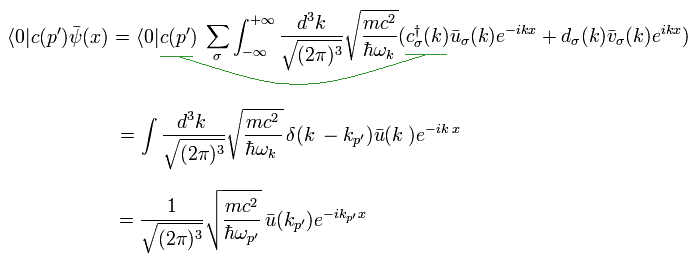
このページに示したように、マクスウェル方程式を満たす 波動関数 A_μ (x), は、
(Eq.31)

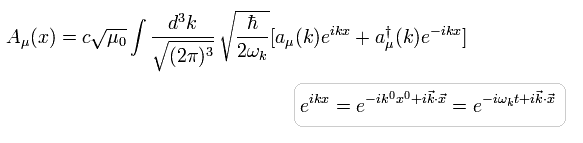
また 各成分の生成・消滅演算子は次を満足する。
(Eq.32)

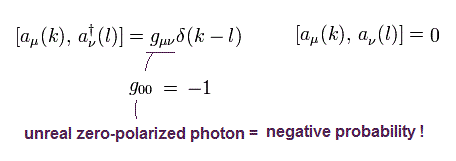
Eq.31 と Eq.32 を用いると、 Fig.17 と Eq.25 の 外線 3 (光子-頂点) は、
(Eq.33)

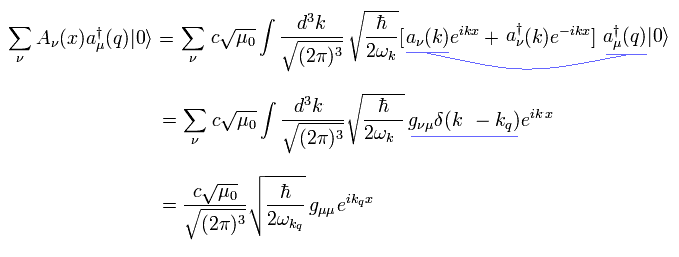
これは 外光子の " μ 成分 " の意味である。
ν が μ に等しくないとき、計量テンソル g_νμ は ゼロになる。

Eq.28、 Eq.30、Eq.33 を d⁴x に関して積分すると、指数関数部分は、
(Eq.34)

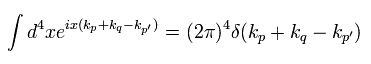
Eq.34 は 運動量とエネルギーの保存を意味している。
( p^μ + q^μ = p'^μ )

１ 頂点では、Fig.17 に示すように ループを含んでいないため 発散しない。
g_μμ のために、 頂点の γ 行列 (Eq.25, Eq.33) は γ^μ に変化する。

[ ２つの頂点関数 G₁ はゼロになる。 ]

次に Eq.24 における ２つのハミルトニアン密度と２つの積分 を含む ２頂点について考える。

(Eq.35)

Eq.35 に示すように、ペアになれない １つの A(y) の演算子が残っている。
この A(y) は 異なった項に属する 生成、消滅演算子を含む。
つまり 両サイドの真空に挟まれて、Eq.35 は ゼロになる。
結果的に ２頂点関数に関しては考慮する必要はない。

[ 発散する １ループ・３頂点関数。 ]

次に Eq.24 の ３つの頂点関数について計算する。
このケースは Fig.18 と Eq.37 に示すように ３ハミルトニアンと３つの積分を含んでいる。

(Fig.18)

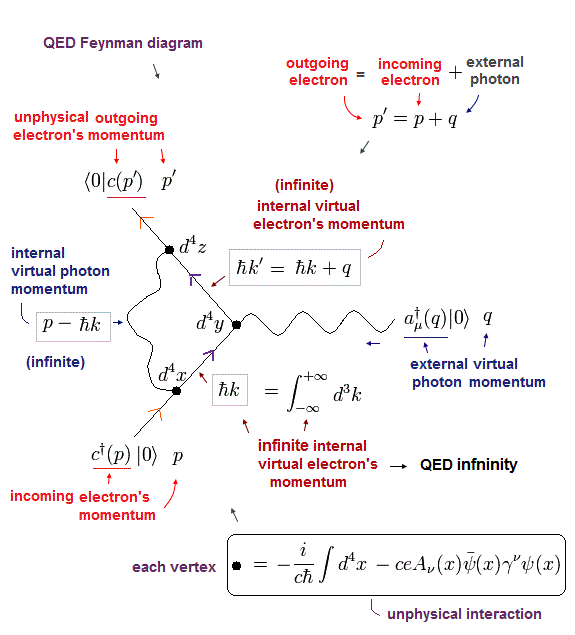
各粒子の 波数と運動量は、
(Eq.36)

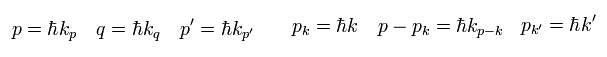
(Eq.37)

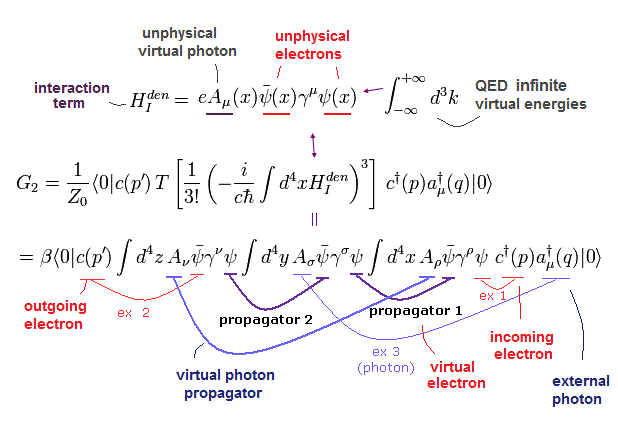
Eq.37 に示すように すべての演算子は ペアを形成するため、ゼロにならない。
指数関数の展開式の係数 1/3 ! は Eq.37 の ３つの頂点の並べ方が ６パターン ( 6 = 3 × 2 ) あるため、キャンセルされる。

[ 無次元の微細構造定数 α は １ループ関数に含まれる。 ]

Eq.37 (Fig.18) と Eq.25 (Fig.17) を比べてみると、 G₂ 関数のほうは ２つ余分な頂点 (積分) を G₀ よりも含んでいる。
(Eq.38)

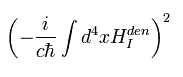
そこで ここでは 繰り込んだ頂点の γ 行列を計算する。
(Eq.39)

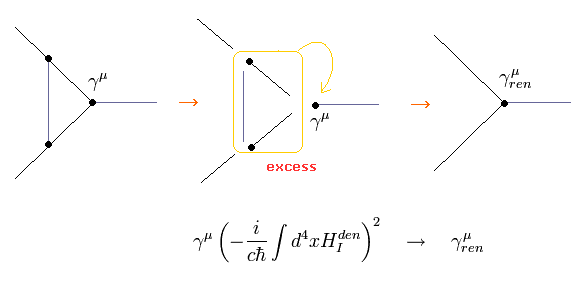
Eq.38 と Eq.39 は ｇ因子を最初に得るときに定義した単なるルールである。
基本的に、指数関数部分の ikx と iωt は 次のように 無次元である。
(Eq.40)

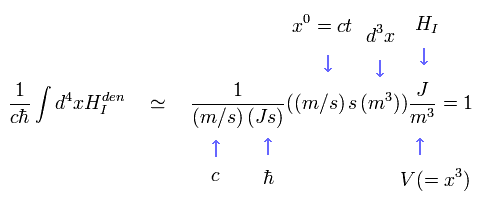
微細構造定数 α も 次のように無次元である。
(Eq.41)

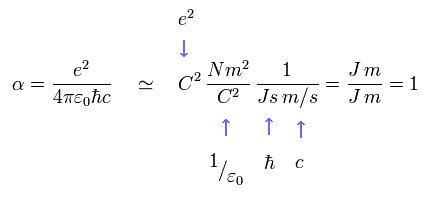
Eq.38 は ２つの ハミルトニアン密度に ２つの電荷 e を含んでいる。
結果的に Eq.38 は 後で説明するが、微細構造定数 α を含むことになる。
（ 注意： Fig.18 は ３つの頂点を含んでいるが、そのうちの１つは Fig.17 に もともと存在している。）

[ ３頂点関数の計算。 ]

３つの外線は G₀ の Eq.28、Eq.30、Eq.33 と 同じである。
つまり 頂点に入ってくる 外電子 ( ex 1 ) は、
(Eq.42)

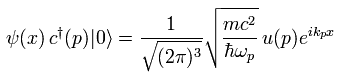
また 頂点を去る 外電子 ( ex 2 ) は、
(Eq.43)

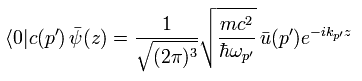
頂点に入る 外光子 ( ex 3 ) は、
(Eq.44)

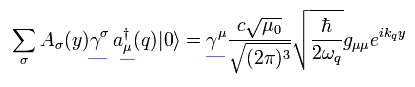
ここで 頂点 γ が γ^μ に変化している。
これは重要である。

Eq.19 と このページを用いると、 フェルミ粒子の 伝播関数 1 ( pro 1 ) は、
(Eq.45)

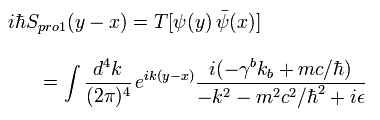
ここでは
(Eq.46)

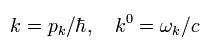
p_k は 運動量で、 ω_k は 角振動数である。

Eq.45 に示すように、伝播関数 ( 内線 ) は 無限種類の運動量とエネルギーを含んでいる。
これは 想像するのは難しいが、QED は 非常に弱い電磁相互作用においても 無限種類の粒子、反粒子の生成・消滅を必要とする。
（ つまり、QED には もともと "リアリティー" がないのである。）

同様に フェルミ粒子の 伝播関数 2 (pro2) は、
(Eq.47)

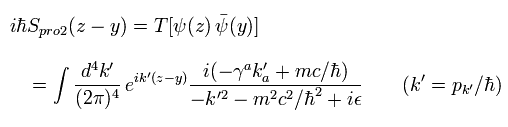
Fig.18 に示すように、 p_k' = p_k + q であり、運動量とエネルギーの保存則を意味している。

Eq.20 を用いて、光子の 伝播関数 3 (pro3) は、
(Eq.48)

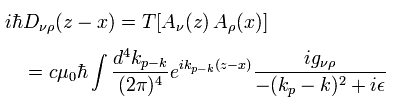
ここで k_p = p / ħ である。

Fig.18 は ３つの積分を含んでいる。 最初に d⁴x に関して積分する。
Eq.42、 Eq.45、 Eq.48 は e^ix を含んでいるので、
(Eq.49)

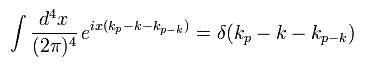
ここでは ３つの伝播関数のうちの１つの (2π)⁴ を使用した。

Eq.49 を Eq.48 の伝播関数に含まれる d⁴k_p-k で積分すると、
(Eq.50)

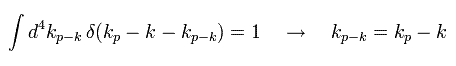
Eq.50 は 外電子 (ex 1) が Fig.18 に示すように 伝播関数 1 と 3 に 分離されることを意味している。

Eq.44、 Eq.45、 Eq.47 は e^iy を含んでいるので、d⁴y で積分すると、
(Eq.51)

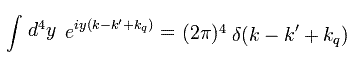
重要な点は ここでは 伝播関数由来の (2π)⁴ を使用できない。
なぜなら Eq.51 の頂点は Fig.17 の G₀ に もともと存在しているからである ( Fig.17 と Fig.18 を比較するように )。
Eq.51 では、 (2π)⁴ は 左辺に含まれていない。
G₂ は ２頂点と３つの伝播関数 を余計に含んでいる ( Eq.39 も参照のこと )。
もちろん これらの定義は 人為的なルールであるが・・。

次に Eq.51 を Eq.47 の 伝播関数 2 に含まれる d⁴k' で積分する。
(Eq.52)

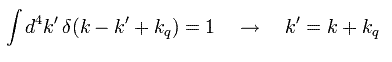
Eq.52 は、 k と 光子 q が 結合して k' になることを表している ( Fig.18 も参照のこと )。

Eq.43、Eq.47、Eq.48 は e^iz を含んでいる。そのため d⁴z で積分すると、
(Eq.53)

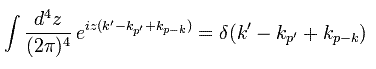
Eq.53 は 伝播関数に含まれている (2π)⁴ を使ってもいい。
( 結果、 １つの (2π)⁴ のみが残る。)

Eq.50 と Eq.52 を Eq.53 に代入して、
(Eq.54)

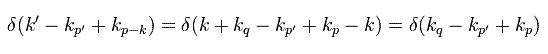
Eq.54 は 次の保存則を意味している。
(Eq.55)

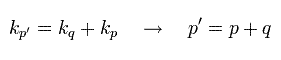
お気づきのとおり、Eq.54 では、 k は 打ち消されるため、 d⁴k で積分する必要はない。
そのため 伝播関数 1 (Eq.45) の d⁴k のみ 残る。
もちろん この積分は -∞ から +∞ なため、無限大に発散する。

(Eq.56) １ループ補正のまとめ。

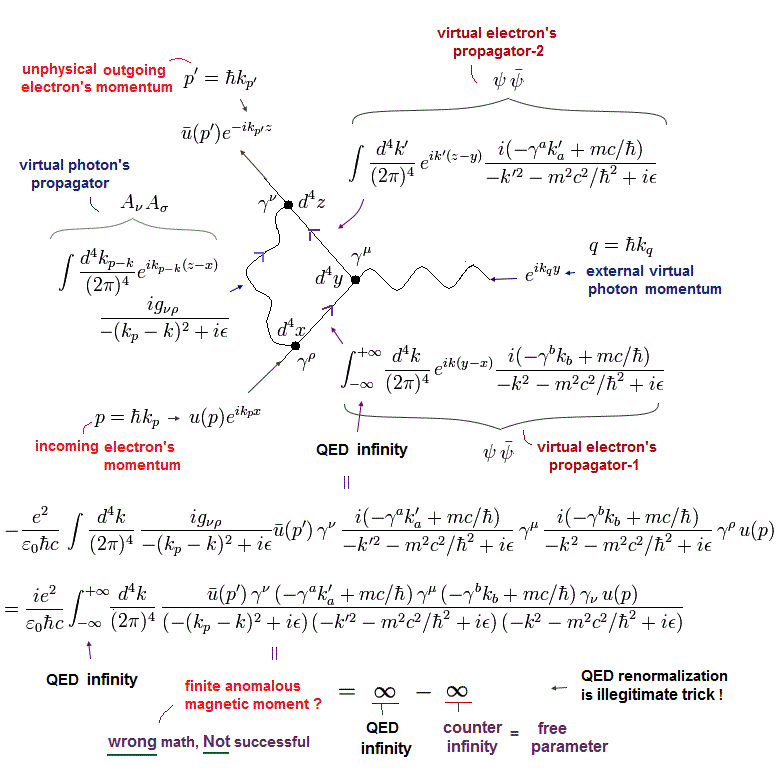
結果的に Eq.56 (= ３つの伝播関数 と２つの頂点 ) の係数は、
(Eq.57)

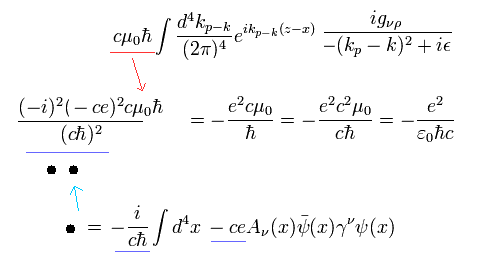
ここでは、
(Eq.58)

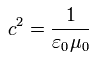
Eq.57 は 無次元なため、 次の 微細構造定数 α に似ている。

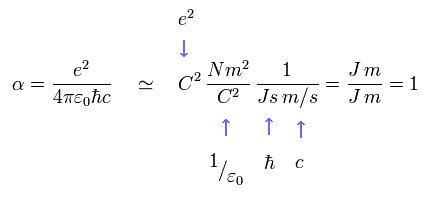
Eq.57 の係数と、Eq.45、 Eq.47、 Eq.48 の３つの伝播関数と ２つの頂点 (= γ ) の残りから 次を得る。
(Eq.59)

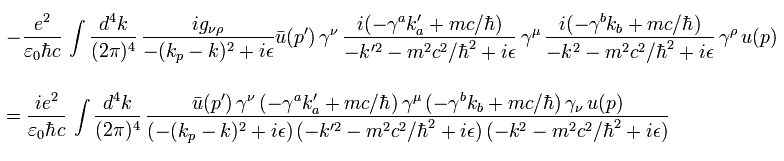
Eq.59 の２行目では 次を使用する。
(Eq.60)

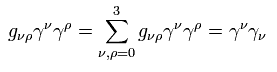
これは非常に重要である。
上で述べたように "非実在" の ゼロ成分の光子が 伝播関数の計算に必要不可欠な理由は ここにある。
( Eq.60 の g_νρ は これらの光子に起因している。 )

次に Eq.59 の分子について計算する。
次の γ 行列の公式を用いる。
(Eq.61)

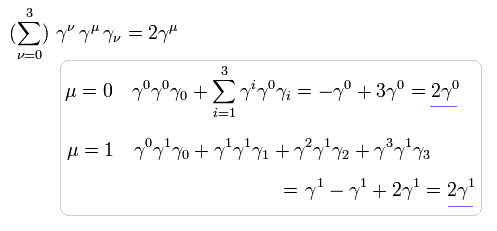
ここでは 次を使っている。
(Eq.62)

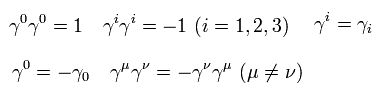
すると Eq.59 の分子に含まれる １つの項は
(Eq.63)

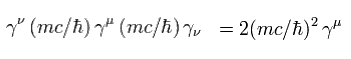
また 次の公式を用いると
(Eq.64)

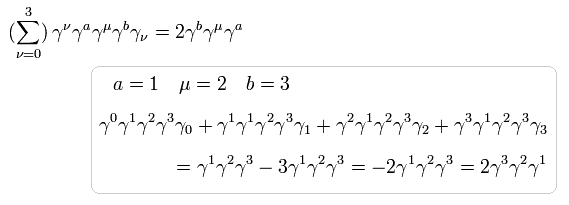
Eq.59 の分子内に含まれる 別の項は
(Eq.65)

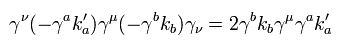
また 次の公式を使う。
(Eq.66)

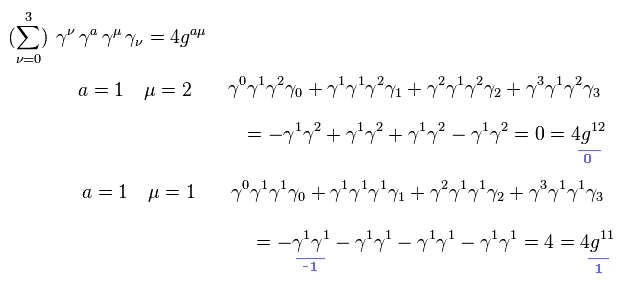
Eq.59 の分子の残りの項は
(Eq.67)

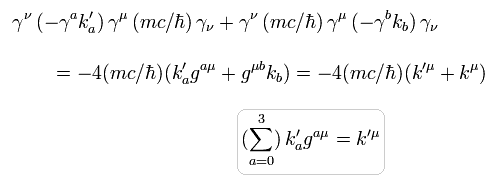
Eq.63、Eq.65、Eq.67 より、 Eq.59 は
(Eq.68)

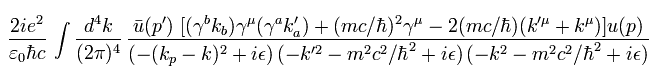
もし ( +1, -1, -1, -1 ) バージョンの計量テンソルを使用し 次のような変換をすると、
(Eq.69)

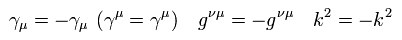
( 付録も参照のこと。 )

Eq.68 は 次のように表せる。
(Eq.70)

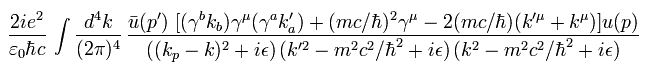
ここから 次の定義を用いて Eq.68 の表現を簡単にする。
(Eq.71)

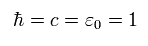
Eq.71 を用いて、 Eq.68 は、
(Eq.72)

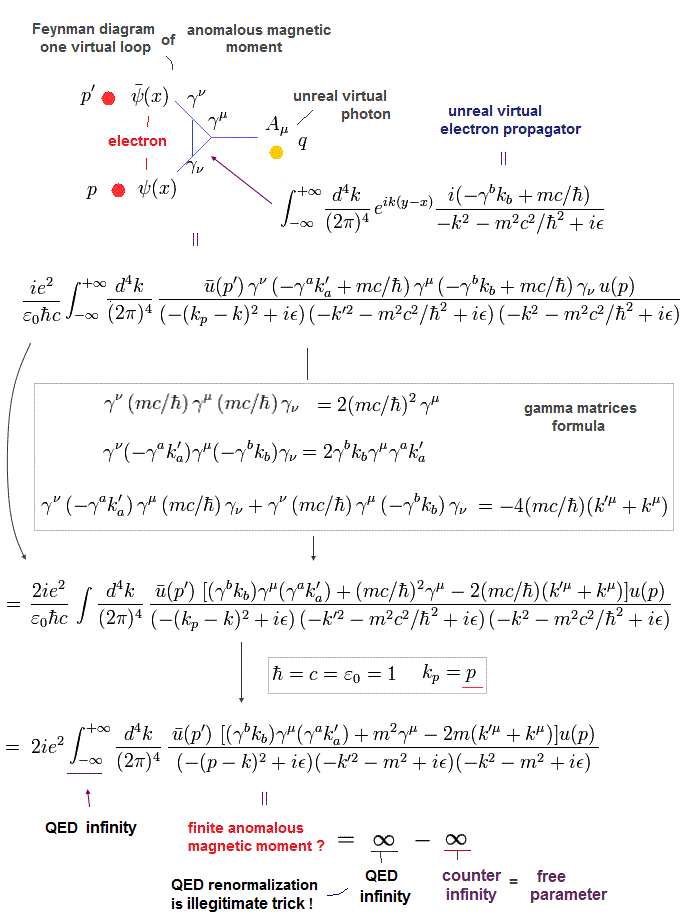
ħ = 1 のために、次のように表記を変更する。
( 例えば、 k_p の代わりに 運動量 p を使用できる。)
(Eq.73)

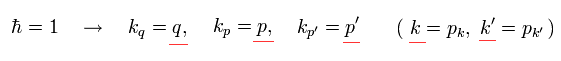
"赤線" の表記をここから使用することにする。

QED における 様々な数学的なトリック。

[ ファインマンパラメーター。 ]

次に Eq.74 の等式を用いて、Eq.72 の分母の３つの式を まとめる。
(Eq.74)

最初に Eq.74 を証明する。
Eq.74 の 右辺を z に関して積分すると、
(Eq.75)

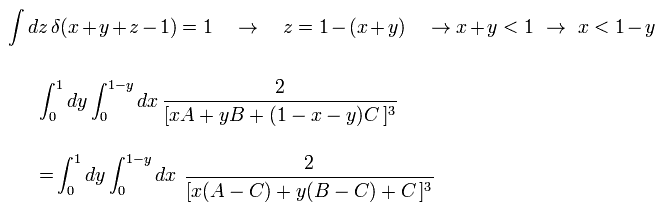
さらに Eq.75 を x に関して積分する。
(Eq.76)

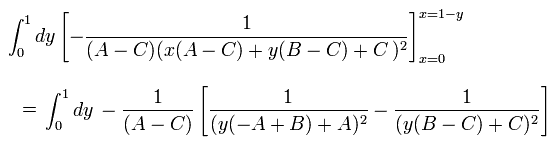
最後に Eq.76 を y に関して積分する。
(Eq.77)

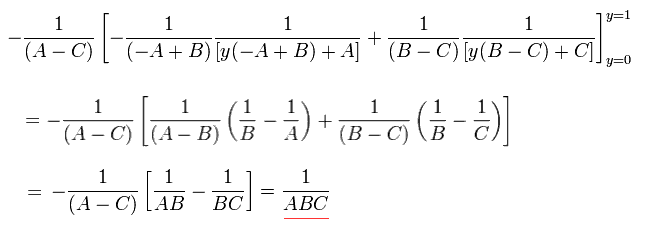
Eq.74 を証明することができた。

[ 任意の定数の平行移動が QED のトリックである。 ]

Eq.74 を用いて、Eq.72 の分母は D³ で表され、 その D は、
(Eq.78)

ここでは x + y + z = 1 と k' = k + q の関係式 ( Eq.52 参照 ) を使用する。
Eq.78 の表記の意味は
(Eq.79)

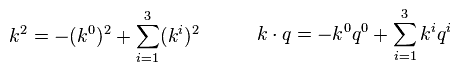
ここで 新たな変数 l を導入する。
(Eq.80)

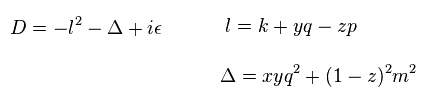
Eq.80 は QED における 重要なトリック の１つである。
l と k は -∞ から +∞ の範囲である。
これは 定数のシフトによる変数変換である。 ( 積分で " l " が " k " に取って変わってる。 )
繰り込みで l² の部分を人為的に除去すると、私達が欲しい 重要な "p" と "q" の値が残る。

Eq.80 が Eq.78 に等しいことを示すには、次のクライン・ゴルドン (質量殻) の定義を用いる。
(Eq.81)

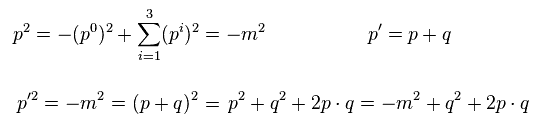
Eq.81 より、次を得る。
(Eq.82)

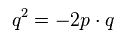
Eq.81、 Eq.82、 x+y+z =1 より、 Eq.80 が Eq.78 に等しいことを示せる。
( 結果的に Eq.72 の分母は D³ となる。 )

Eq.80 より、
(Eq.83)

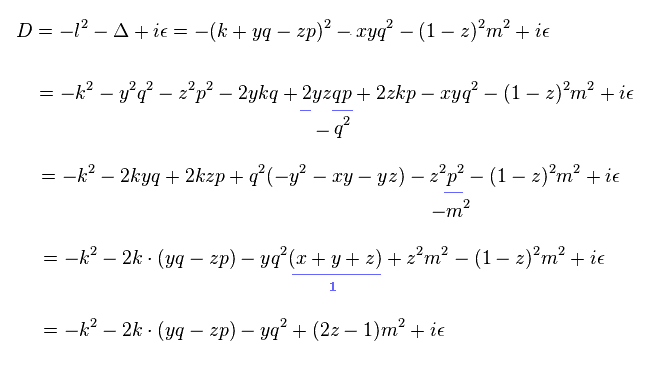
Eq.81、x+y+z=1 を用いると、Eq.78 の最後の２つの項は
(Eq.84)

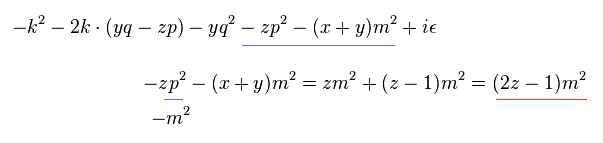
Eq.83 は Eq.84 に等しい。
つまり Eq.78 は Eq.80 に等しい。

[ もともと １ループには 外電子は含まれていない。 ]

次に Eq.72 の 分子が 次のように表せることを示す。
(Eq.85)

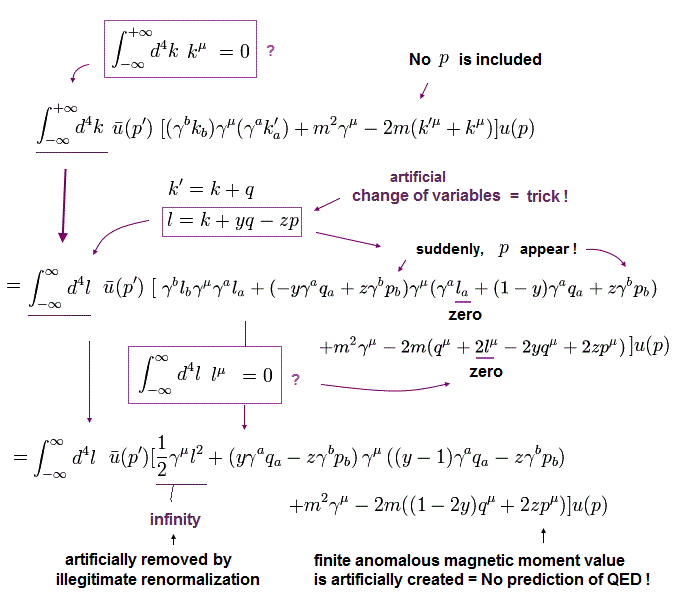
Eq.85 の詳細な計算方法に関しては 付録に示してある。

Eq.85 の 最初の行に注目すると、それは "外電子" ( p や p' ) を含んでいないことが分かる。
k' = k + q。 k や k' は 無限種類の運動量を持つ 仮想粒子である。
"p" の初期情報がなければ、これらの無限の仮想粒子は 電子や ｇ因子と何の関係もなくなる。

(Eq.86) 定数の平行移動で "p" が 現れる。

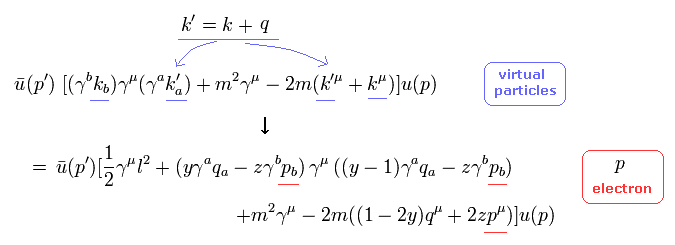
しかし Eq.85 (Eq.86) の２番目の行で、外電子 (p) の情報が含まれている。
このトリックは 積分変数における 定数のシフトにある。

(Eq.87) 積分変数の操作。

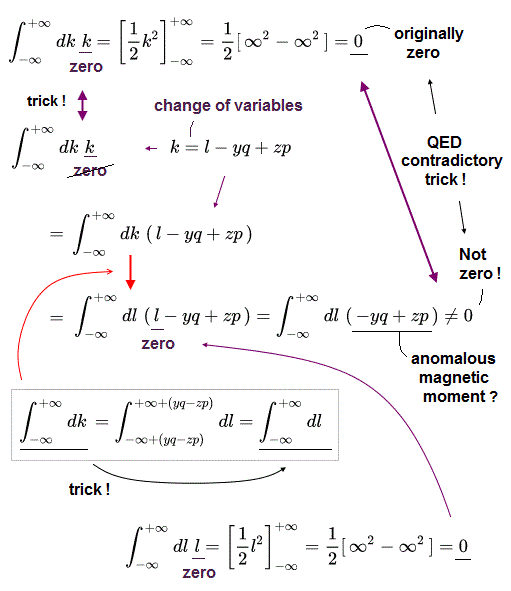
Eq.87 に示すように、 新しい変数 l は、 k を ある定数だけ シフトして作る。
この定数には 外電子 (= p ) の情報が含まれている。
また、 l² の項は 繰り込みによって 人為的に除去される。これが QED の数学的トリックの１つである。

[ 間違った数学 II ]

" l " が １つの項は 奇関数のため 積分で取り除かれる。しかし この数学にも間違ったものが使われている。

(Fig.10') この数学は正しいのか？

Fig.10' の上では、"k" は奇関数のため 積分するとゼロになる。
積分変数を変換すると ( k = l - β )、" l " の項が 奇関数のため 積分でゼロになる。
結果的に "-β" の部分のみ残り、ここに ｇ因子の情報が含まれていることになる。
この数学的手法は QED の ｇ因子の値を得るのに 必要不可欠なものであるが、あたながたは Fig.10' の数学が正しいものだと思われるだろうか？

(Fig.10'') 正しい数学。

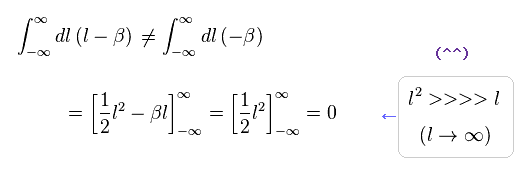
Fig.10'' は 正しい数学を用いたものである。この正しい数学によれば、もちろん "-β" の項もゼロになることはいうまでもない。
なぜなら、それらを積分すると、 " l² " の項が " βl " の項の部分よりも はるかに早く発散するからである。
結果的に " l² " の項のみ残り、この結果はゼロになる。
( 正しい数学によれば、 "β" の部分は "l" の項に吸収されてなくなってしまう。 )
つまり Fig.10' の QED の数学的手法は 数学の基本を破っているのである。

[ 間違った数学の応用。 ]

ここで 実際に ｇ因子の計算に使用されている "間違った数学" の例に関して説明する。
もちろん、間違った数学が実際に使用されているならば、QED の ｇ因子は間違いということになる。
なぜなら 単なる 計算ミスだからである。
(Eq.W-1)

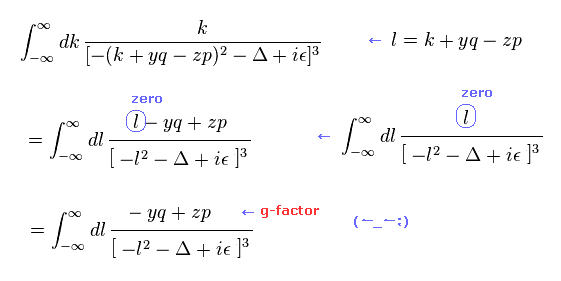
Eq.80 に示すように、 元の " k " の変数を " l " に変換した。
よって 分子に含まれる 奇関数 " l " の部分は 積分によってゼロになる。
( 分母は l の偶関数 である。 )
結果的に ｇ因子 (= p ) の含まれる部分の項のみ残ると 彼らは主張しているのである。
Eq.W-1 は 正しいように見えるが、実際は この数学は間違っており、よって QED の ｇ因子も間違いということになる。

(Eq.W-2)

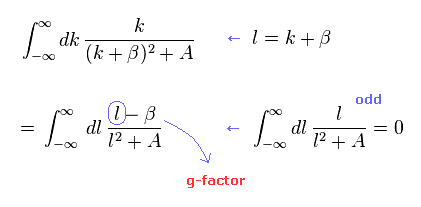
有理関数の積分に関して Eq.W-2 の簡単な例を用いて説明する。
変数 " k " を " l " に変換すると、奇関数の部分は 積分でゼロになる。
結果的に ｇ因子の部分のみ残る。
(Eq.W-3)

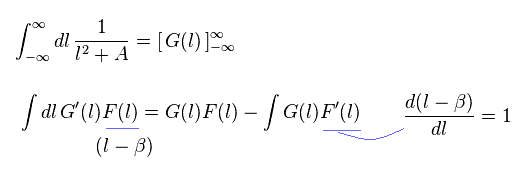
ここで Eq.W-2 の分母の積分したものを G(l) で表すことにする。
そして Eq.W-3 に示すように 部分積分すると、
(Eq.W-4)

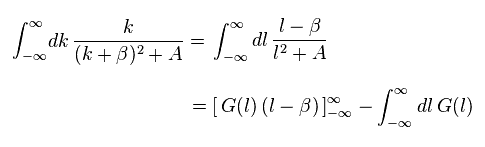
( l - β ) の部分を 単に l に変換しても、無限大 ( もしくは マイナス無限大 ) は 無限大 ( もしくは マイナス無限大 ) の ままである。
(Eq.W-5)

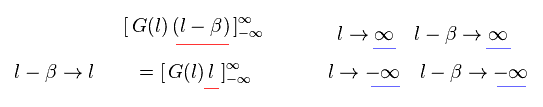
Eq.W-5 を用いると、Eq.W-4 の結果もゼロになる。
(Eq.W-6)

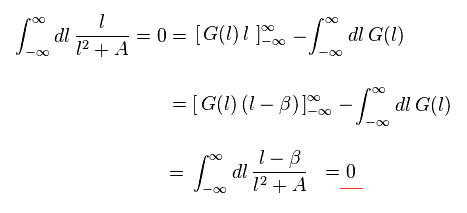
つまり ｇ因子の部分のみピックアップして取り出す 数学的手法は 間違ったものなのである。
(Eq.W-7)

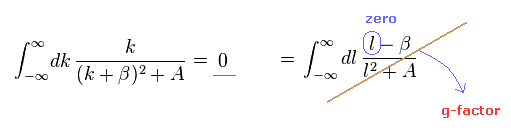
Eq.W-7 の分母では "k²" の項の無限大が優位になるため、k と l の違いがなくなるのである。
結果的に Eq.W-7 もゼロになる。

これはつまり QED の ｇ因子は 間違った数学に依存しているのである。
もちろん、私達が それらの数学が間違いだと知った以上、QED が 真実を語ることはあり得ない。

Eq.W-3 のように、 次のように定義すると、
(Eq.W-8)

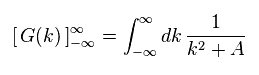
Eq.W-7 は、
(Eq.W-9)

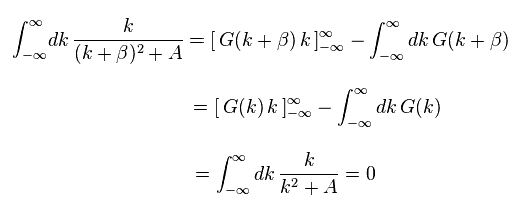
Eq.W-9 の結果は Eq.W-6 のものにちょうど等しい。
２つのアプローチで 同じ結果が得られたので、この結果は正しいことになる。
結果的に Eq.W-2 のように オリジナルの式から ｇ因子の部分のみ ピックアップすることはできないことになる。

(Eq.W-10)

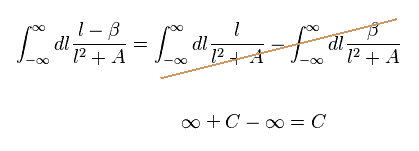
Eq.W-4 では、式を ２つの項に分離した後 それぞれを別に計算することは正しくない。
なぜなら、例えば もっと高次の式では、 ∞ + C - ∞ = C のように間違った結果を得てしまうからである。
有限の値 "C" は 無限大の中では 無視されなければならない。また この結果は Eq.W-9 のものと一致しない。

次に Eq.85 (= Eq.88 の "1" ) が 次の式に等しいことを示す。
(Eq.88)

詳細な計算方法については 付録を参照のこと。

異常磁気能率と磁場における矛盾。

[ 外磁場における矛盾。 ]

このページに示したように 次の関係式を得ることができた。
(Eq.89)

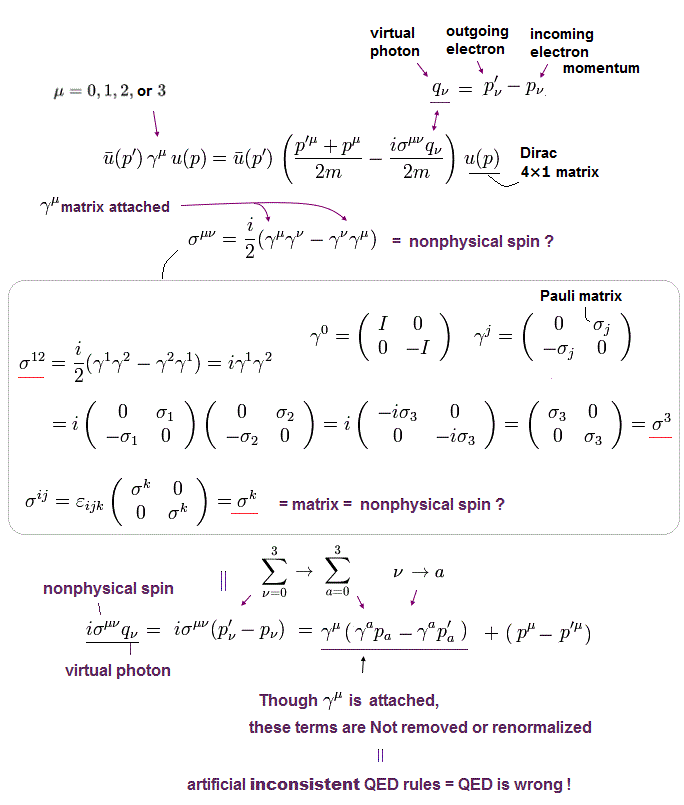
ここでは
(Eq.90)

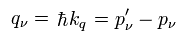
この "q" は ( 仮想 ) 光子 = 外磁場である。
この定義によれば、電子の運動量 (= 速度 ) が 定常 ( p' - p = 0 ) のとき、外磁場は存在してても ゼロになってしまう。
これは奇妙である。

(Fig.19) 外磁場 B = 0 ？

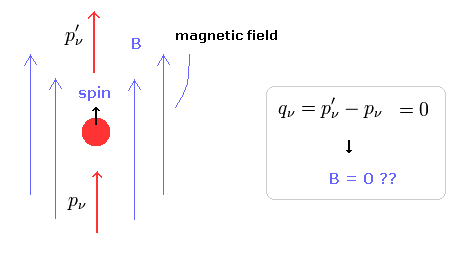
Fig.19 では、電子は z 方向 に動いている。
また 外磁場 "B" も z 方向 である。

ローレンツ力は、
(Eq.91)

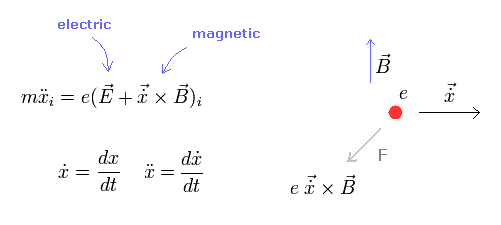
( Fig.19 では、 E を ゼロとしている。 )

Fig.19 では スピン・磁気相互作用 があるにも関わらず、Eq.89 の定義では 外磁場がゼロになってしまう。
なぜなら 電子の運動量は 外磁場によって変化しないからである ( p' - p = 0 )

[ スピンｇ因子の繰り込み。 ]

Eq.89 から、
(Eq.92)

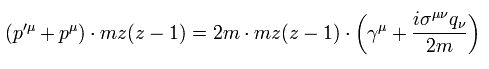
Eq.92 を Eq.88-2 に代入すると スピン・磁気相互作用が出現する。
(Eq.93)

(x-y) の 反対称性より、 x と y の積分によって Eq.93 の最後の項は消える。
つまり Eq.72、 Eq.74、 Eq.80 (= D ) より、 Eq.93 は 次のように表せる。
(Eq.94)

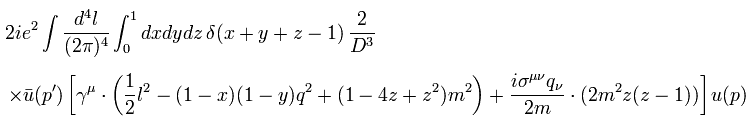
ここでは
(Eq.80)

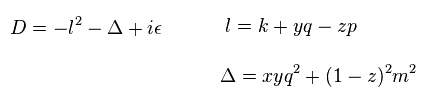
ここでは l² の積分において "ウィック回転" を使う。
極の位置と、積分関数が l の大きい範囲で ゼロになっていくことより、積分曲線を 90 度回転できる。
そこで 次のように ユークリッド空間の４元運動量 l^E を定義する。
(Eq.95)

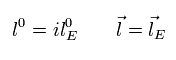
Eq.95 を用いて、
(Eq.96)

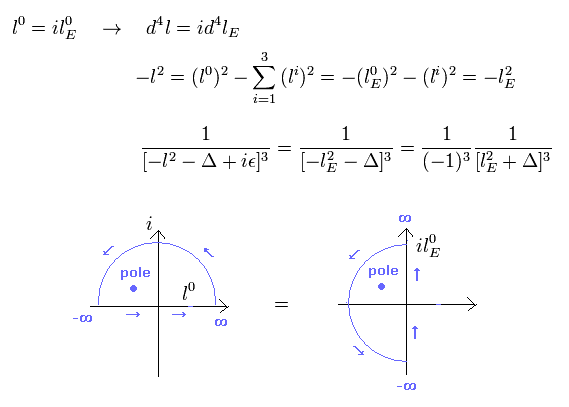
l_E の変数に変換することによって、４次元の極座標を考慮できる。
例えば、 1/D³ は、 ( Eq.96 を用いて )
(Eq.97)

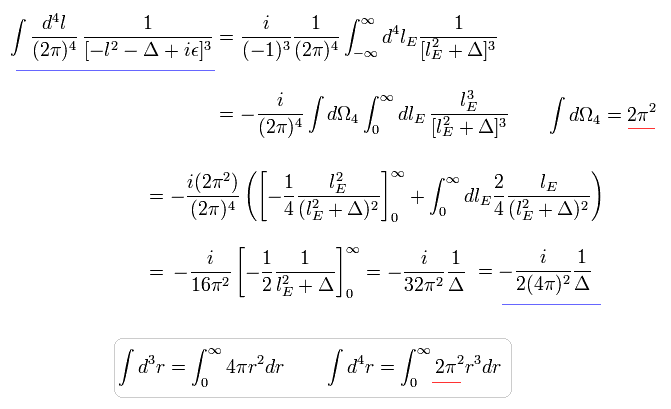
ここでは ４次元の単位球を使用している。

しかし 次のケースでは 積分が 無限大に発散する。
(Eq.98)

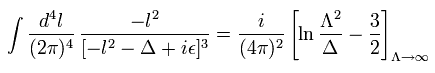
これを "紫外発散" という。

Eq.97 と Eq.98 を用いて、Eq.94 は、
(Eq.99)

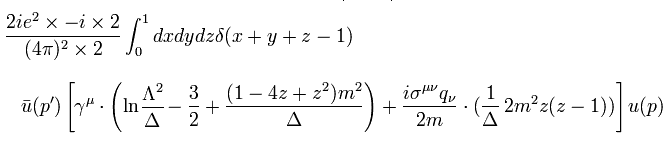
ここで q² を ゼロ とした。
最初の章で述べたように、この q² が ゼロになった瞬間、仮想光子のエネルギーは ゼロになる。
つまり q = 0 のとき ｇ因子は 単一の値に固定できない、QED ｇ因子は 真実ではない。

微細構造定数 α (Eq.41) を使用すると、Eq.99 の係数は 次のように表せる。
(Eq.100)

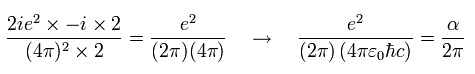
Eq.68 も参照のこと。

さらに Eq.99 の２項目も q² = 0 のとき、発散する。
(Eq.101)

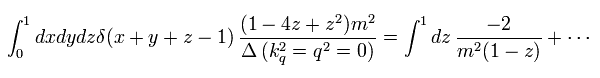
これを "赤外発散" という。

Eq.99 の これらすべてのやっかいな値を 繰り込みで除去する。
(Eq.102)

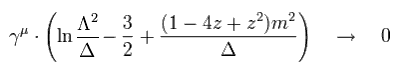
"相殺項" は 粒子が "質量殻"を満たす条件より得られる。
つまり Eq.102 自身が 相殺項となり 自身を打ち消す。
そして これらのトリックは 奇妙な 無限大の 裸の電荷や質量を生じさせる。
非常に人為的な操作である。

Eq.99 で最後の項が残った。
この項 (= ボーア磁子 ) の係数は、
(Eq.103)

これを "形状因子 2" という。

q² = 0 のとき、 Eq.103 は、
(Eq.104)

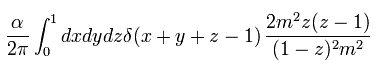
幸運なことに、 Eq.104 は 次のように収束する。
(Eq.105)

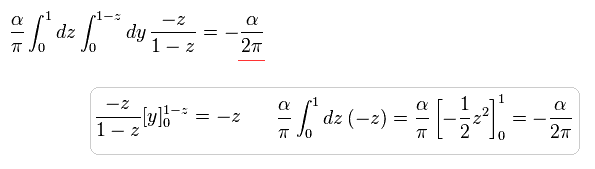
結果、 Eq.89 は、
(Eq.106)

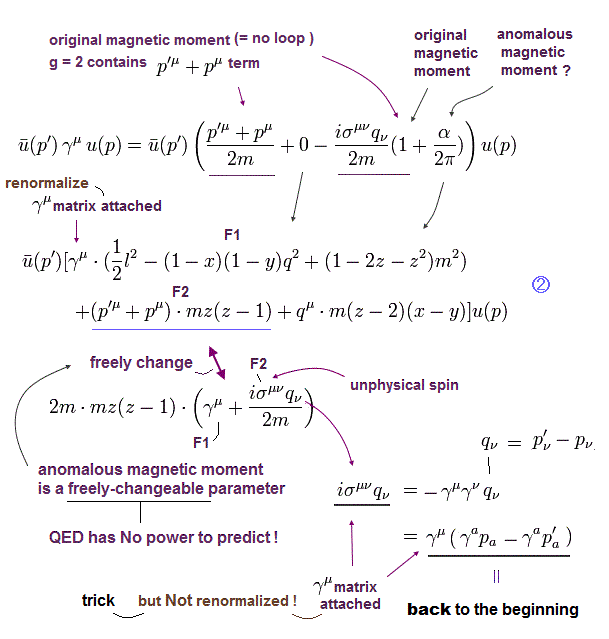
電子のｇ因子の補正は、
(Eq.107)

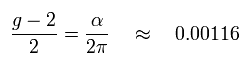
Eq.107 の実験値は 0.0011597 である。
( これを "異常磁気モーメント" という。)
つまり １ループのみで 実験値とほぼ同じ値を得ることができる。

Eq.103 と Eq.104 に示したように q² = 0 の条件は ｇ因子の値を得るのに 必要不可欠な条件である。
すでに述べたとおり、仮想光子が アインシュタインの質量公式 ( q² = 0 ) を満たした瞬間に、そのエネルギーと運動量は すべてゼロになる。
このページに示したように、この非常に緩い制限のもと、QED は ありとあらゆる ｇ因子の値を与えることができる。
これはつまり 自然界の法則は 異常磁気能率の決定に際し、QED に従っていないということである。

また 無限種類のループを含んでいるため、すべてを計算すること自体も不可能である。

2013/1/25 updated This site is link free.