
トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは存在しない。
現在の物理の説明が分かりにくい理由。
(Fig.1) ボーア軌道の加速する電子の電磁波放射 ? = " マインドコントロール "の1つ。

通常の教科書は よく古典的なボーア軌道の 加速する電子 は エネルギー放射して 核に落ちていくと述べている。
しかし 残念ながら これらの説明は完全に間違いである。
この主張は ポインティングベクトル (= E × H ) を エネルギーの流れとして用いている。
この ポインティングベクトルは 真空における 電場、磁場のエネルギーの変化を表している。
この真空における電場エネルギー (= 1/2εE2 ) は ( Fig.1 左 ) に示すように 中心の導体球に マイナスもしくはプラスの無限小電荷を 集めるのに必要な ポテンシャルエネルギーを意味している。
しかし 単一電子は それより小さな電荷の集まりではない ( 単一電子は 最小の電荷である )。
これはつまり 真空の電場エネルギーは 単一電子においては エネルギーではないことになる。
すなわち ポインティングベクトルは 単一電子の場合は エネルギーの流れを意味していない。
( このページも参照のこと。 )
つまり これらの説明は ボーア軌道に関する 一種の "マインドコントロール" のような役目を果たしていると考えられる。
(Fig.2) シュレディンガー方程式は ボーア・ゾンマーフェルトの一部である。
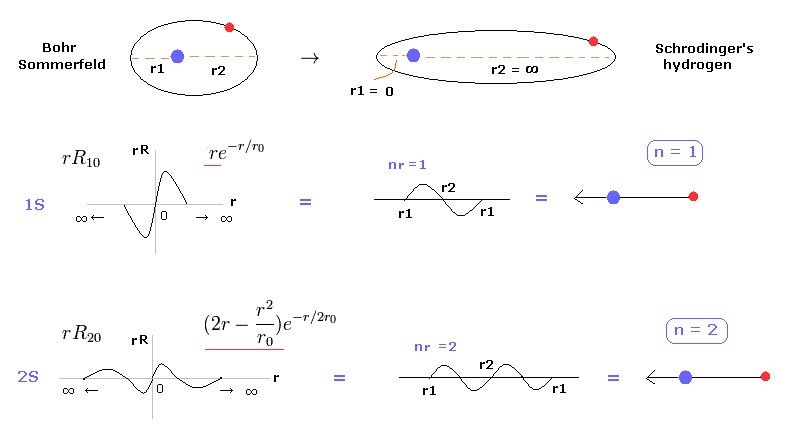
たいていの教科書には 「 ボーア模型の水素は "偶然に" シュレディンガー方程式の結果や実験結果に一致した。」 という説明をよく見かける。
しかし 真実とまったく関係のない模型が 正確な結果を出せるということは 極めて不自然なことである。
実際に このページで シュレディンガーの水素原子も ボーア模型のように 整数倍のドブロイ波長の原理を用いていることを示した。
分子軌道法 (= MO ) は 様々な水素原子の励起状態の組み合わせを用いて正確なエネルギー状態をだそうとしている。
このページでは、 2p、 3d などの励起状態は ドブロイ波長の整数倍条件を保ったまま 軌道の形を変更できる。
つまり 根本的に それらは ボーア模型と同じ原理を用いているのである。
重要な点は 通常の教科書が ボーア・ゾンマーフェルト模型が ディラック方程式と全く同じ微細構造 の値を与えるという事実を 隠しているという点である。( このページも参照のこと。 )
(Fig.3) 炭素様原子の正四面体構造。
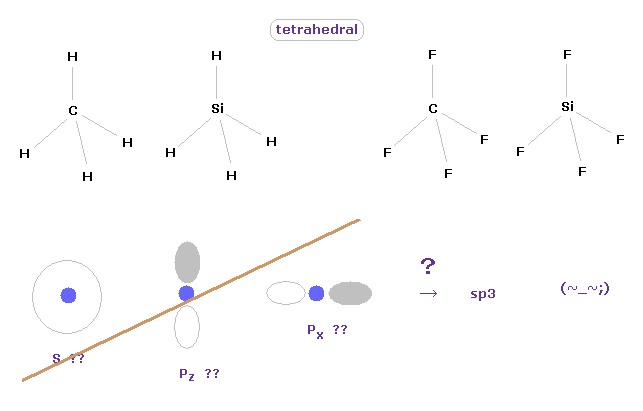
量子化学における アブ・イニシオ " ab initio " 法は 正確な値が得られると言われている。
しかし 実際には 様々な分子の形を得るために 様々な係数などを人為的に 調整する必要がある。
メタンが 正四面体の構造をしていることは 通常の古典力学の観点から 容易に思い浮かべることができる。
これらの 正四面体 ( もしくは 正八面体 ) 構造を 量子化学を用いて表そうとすると、2s, 2p-x, 2p-y などを 正確な値にマッチするように組み合わせる必要がある。
ab initio 法で使われている基底関数系は STO、GTO、3-21G などにおいて 各異なった分子ごとに 人為的に決定される。
要するに どの基底関数系を選ぶかが 量子化学において最も重要な概念と言える。
(Fig.4) 各原子ごとに 適切な基底関数を選ぶことが重要である。

"ab-initio" 法は 初期条件(= 関数 ) に依存しないと言われている。
しかし 実際の計算では これは単なる理想論にすぎない。
実際には 彼らは ab-initio 法では 各原子に対して 異なった基底関数を用意する。
例えば、6-31 G では 彼らは 1s、2s、2p において 異なったサイズのペアを選んでいる。
( 水素 -- 1s, 1s'、 炭素 -- 2s, 2s', 2p, 2p' )。
これらのサイズは 実験結果に合うように あらかじめ スケーリングファクターを 人為的に 操作することによって 決定される。
そして もしこれでも良い結果が得られなければ、他のタイプの 分極関数 や diffuse関数を それらに付け加える。
このようにして、彼らは ただ人為的に 実験結果にマッチする 最適な基底関数を選んでいるにすぎない。
もちろん、これらの基底関数は水素のエネルギ―準位に基づいており、これは ボーア・ゾンマーフェルトの水素に完全に一致したものである。
(Fig.5) 量子力学では 電子は球状に広がっている?

量子力学によれば、私たちは 水素原子内で 単一電子の場所を指定できない。
そのため、量子力学の単一電子は 必ず 波動関数として広がっていなければならない。
例えば 単一電子が 球状に広がっているとすると、そのポテンシャルエネルギーの観点からは その電子が 球の中心にあると見なせる。
もし 電子が中心にあるとしたら、それはちょうど +e の原子核と重なっており、水素原子は完全に中性になってしまう。
すると 水素原子は 他の原子とまったく相互作用できないことになる。
他の原子と相互作用するには 水素原子の電子は ボーア模型のように ある場所に局在化している必要がある。
(Fig.6) H-H 結合 = 2つの電子が互いに避け合っている。

水素分子では、2つの電子が他の原子核に引きつけられている。
しかし もしこの状態を 球状の波動関数を用いて表そうとすると、Fig.5 下図に示すように それらは互いに反発し合うことになる。
一方で 古典軌道を用いると、水素分子を自然に表すことができる。
この自然な模型では、2つの電子が互いに避け合って (= up と down )、他の原子核にひきつけられて 共有結合を形成する。
また このページに示したように、古典的な軌道を用いて 非常に簡単かつ 自然な方法で 水素分子の正しい実験値を得ることに成功した。
結果的に 共有結合を表すには 様々な分子において 具体的に局在化した電子を用いる必要がある。
(Fig.7) "数学上" のシュレディンガー方程式 vs. "リアル" なボーア模型。
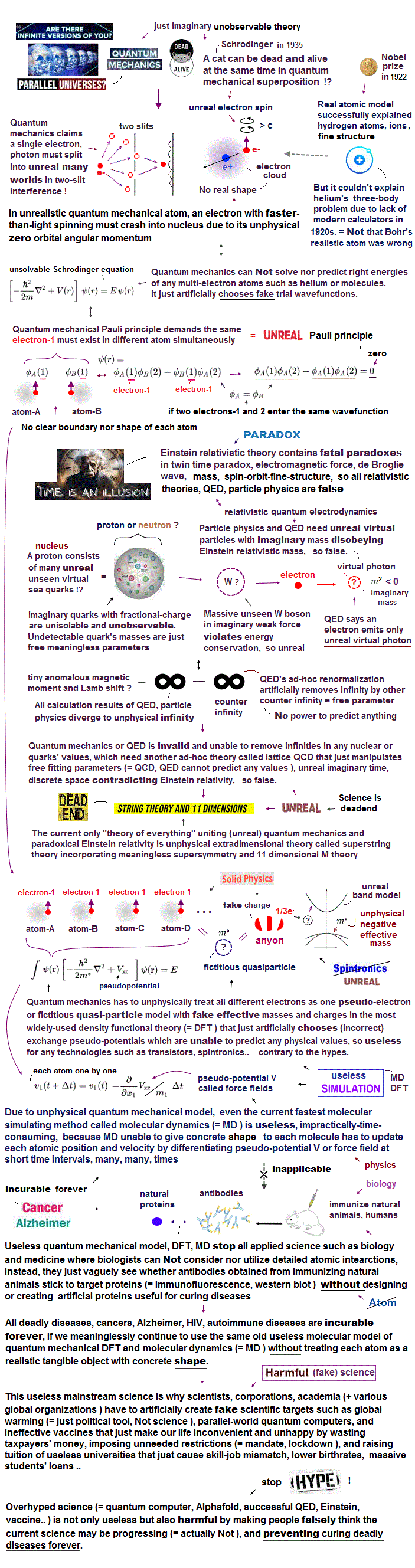
"ab-initio" (= 第一原理 ) 法は 非経験的な方法と言われている。
しかし実際には 各異なった分子ごとに 最適な基底関数を人為的に選ばなければならない。
基底関数系を選んで 通常の Hartree-Fock 法を計算した後に、それらに 完全配置間相互作用 ( CI ) 法、MP法、結合クラスター ( CC ) 法 などを組み合わせる。
Fig.5 や Fig.6 で説明したように、低いエネルギー状態になるためには 電子は 互いに避け合う必要がある。
MO や CI 法では、これらの反発相互作用を表すのに 非常に複雑な行列式を導入している。
なぜなら 行列式では 2つの電子が 同一の状態に入れないからである。
しかし Fig.7 に示したように、これらの非常に込み入った行列式のために、これら役に立たない量子化学を 様々な分子生物学的な相互作用などに 応用することができない。
(Fig.8) これは役に立つの ?
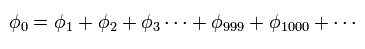
完全配置間相互作用法でさえも、正確な結合エネルギーを得ることはできない。
そのため MP や CC 法をそれらに組み合わせる。
しかし MP や CC 法などの ab initio 法は 実験結果よりも 低くなってしまう 間違った基底状態のエネルギーを与えてしまう。
"ab initio" は 端的に言えば、単に 水素原子のエネルギー準位を利用しているだけにすぎない。
( もちろん、これらの概念は ボーア模型に完全に一致している。重要な違いは 量子力学は 非現実的な多世界 で ボーア模型は 多世界でない という点である。)
彼らは ab initio 法に関して かなり大袈裟に誇張しすぎである。
下記の様々な分子の結合長、結合角はすべて CRC の教科書からのものである。
(Fig.9) メタン ( CH4 )。
様々な分子の相互作用を計算するために このでは このサンプルプログラムを用いる。
( このテキストを "orbit.java" としてセーブして コンパイルしてほしい。 )
詳細な方法に関しては このページをまず参照するように。
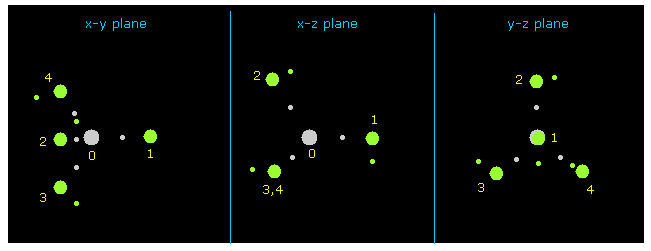
C-H の結合長は 1.8700 Å (= 18700 MM ) で、 H-C-H 結合角は 109.45° (= 正四面体 ) である。
プログラム実行後、 "nucleus" ボタンをクリックして CH4 の絵 が ( その中心が atom 0 の 炭素 ) が x-y、 x-z、 y-z 平面上に表示される。
水素原子は 緑の円、 中心の炭素は 灰色の円である。
(Fig.10) CH4 の水素原子。

それから 指定のテキストボックス内に "1" の値を入力して"electron" ボタンをクリックする。
そうすると、 atom 1 (= この場合は 水素 ) の電子が 画面上に表示される。
ある値 (MM) をテキストボックス内 ( +X、 +Y、 +Z ) に入力して エンターキーを押すと この電子の座標を変更できる。
電子と 水素原子核間の初期距離は 4500 MM (= 0.4500 Å ) にしてあり、これは ボーア半径 (= 約 0.5200 Å ) よりも 少し短い。
なぜなら 水素の電子は 炭素原子核に引きつけられて 少し収縮するからである。
"-5200" (= ボーア半径 ) を "+Z (MM)" に入力して エンターキーを押すと、全エネルギーは tV = -438.16 eV となり、 これは CH4 の 実験値 -439.35 eV とほぼ同じである。 このページも参照のこと。
(Fig.11) 水素の電子の座標の変化。
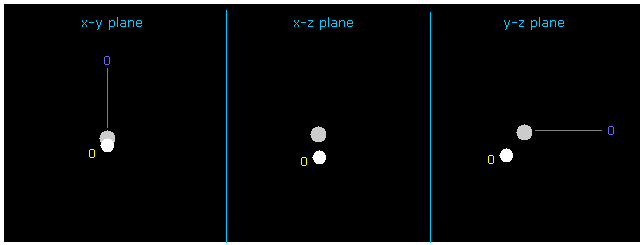
+Y = -1217 と +Z = -3362.0 をテキストボックス内に入力して エンターキーを押すと、この H 電子の位置は変化する。
また この場合は 水素原子核に作用する力も ちょうどゼロになり ( now 1; FX=3, FY=0, FZ=0 )、また そのドブロイ波は ちょうど ave = 1.0000 になる。
しかし この場合は 全ポテンシャルエネルギー (= -480.46 eV ) が 実際の値よりも低くなる。
なぜなら このページで 説明したように、 炭素の価電子においては この特殊な配置のみでなく 平均の分布状態を考える必要があるからである。
炭素の 4 つの価電子は 広く 分布している (= 0.6415 Å 半径 )。
( この特殊な状態では 炭素の 4つの価電子は H 原子核に 最も近づいている。 )
(Fig.12) CH4 における 4つの価電子。
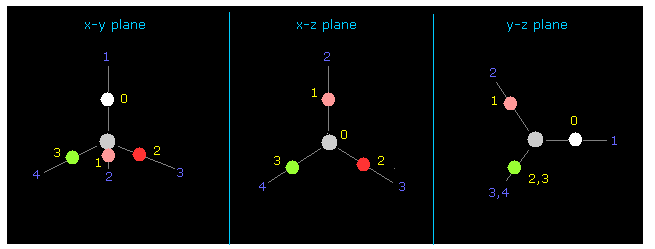
再び それらの間の "-4500" を +Z のテキストボックス内に入力する。
それから "0" を 指定のテキストボックス内に入力して "electron" ボタンをクリックする。
すると、4つの 炭素の価電子 が 画面上に表示される。
(Fig.13) C の電子に作用する 力 (CF)。
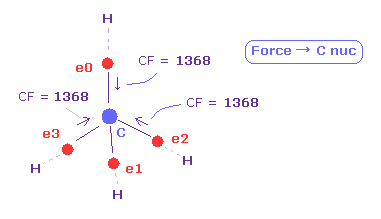
CF (= 各電子に働く力の C 原子核方向の成分 ), CF=1368 は 適切な値である。
この CF は H 電子が ボーア半径のとき "1278" になり、 H 電子の ドブロイ波が 1.0000 のとき、 "1455" になる。
(Fig.14) 力 = 1000.
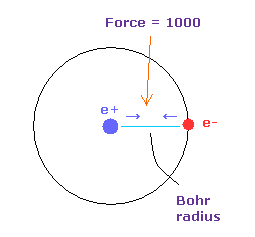
力の単位を Fig.14 に示した。
水素原子核の 電子と原子核間の力を "1000" とする。
そのため 電子と +e の原子核間の距離が ボーア半径のとき、その力は 1000 になる。
例えば 力 1468 は H 原子の基底状態の力の 1.468 倍ということになる。
| C-H 結合長 | CF ( Z = -0.4500 Å ) | CF ( ボーア半径 ) | CF ( wave = 1.0 ) | CF ( 他の ele 1-3 ) |
|---|---|---|---|---|
| 0.9000 Å | -1383 | -1519 | -- | +1382 |
| 0.9500 Å | -121 | -250 | -- | +1377 |
| 1.0000 Å | +636 | +520 | +816 | +1374 |
| 1.0870 Å | +1368 | +1278 | +1455 | +1368 |
| 1.1500 Å | +1660 | +1587 | +1704 | +1367 |
Table 1 は C-H 結合長に応じて 炭素の価電子 0 に作用する力 (= CF ) が どのように変化するかを示したものである。
C-H 結合長は 画面が Fig.9 (= 原子画面 ) のときに自由に変更できる。
atom 1 の "+X (MM)" のテキストボックス内に ある値を入力して エンターキーを押せばいい。
C-H 結合長が 1.0870 Å (= 実験値 ) のとき、 力 CF は 約 1400 になり、これは いい結果である。
CF の 左、中、右は ele 0's の相対座標が それぞれ Z=-0.4500 Å、 Z=-0.5200 Å (= ボーア半径 )、 ドブロイ波が 1.000 のときの CF を意味している。
(Fig.15) 炭素の電子 (= e0 ) が C の代わりに H に引き寄せられる !?
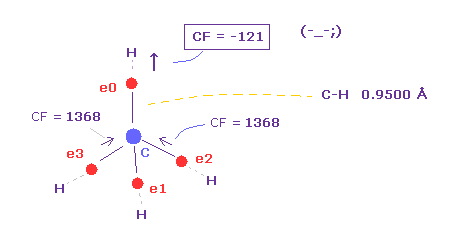
Table 1 に示したように、C-H 結合長が短くなった (= 0.9500 Å ) とき、C 原子核方向への力は マイナス になる ( CF = -121 )。
これはつまり 炭素の価電子 e0 が 炭素原子核の代わりに 水素原子核に引き寄せられることを意味している。
つまり このケースでは、電子と H 原子核は 不安定になってしまう。
また、 C-H 結合長が 0.9500 Å のように短いと、ドブロイ波が 1.000 の状態で H 原子核をストップさせられなくなってしまう。
C-H = 1.0000 Å のケースでも、 CF = 636 は 小さすぎる値である。
( Fig.14 で述べたように、 単純な水素原子内でも、力は "1000" もある。 )
結果的に このページに述べたように、 価電子と原子核の 安定性が メタンの C-H 結合長を 決定していることになる。
(Fig.16) フルオロメタン (= F-CH3 ) 分子。
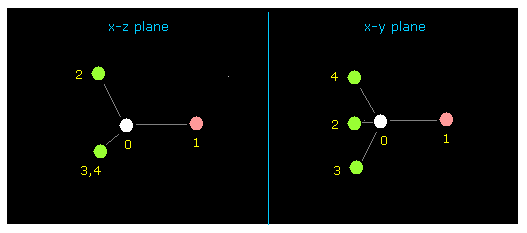
プログラムを実行後、 "0" を入力して methane-like 分子を選択して、それから "1" を入力して F-CH3 を選択する。
詳細な方法に関しては このページも参照のこと。
(Fig.17) フルオロメタン (= F-CH3 )。
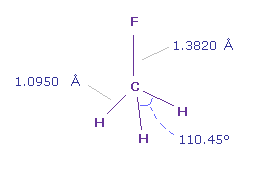
C-F 結合長は 1.3820 Å で C-H 結合長は 1.0950 Å である。
画面上には、 フッ素 (= F ) 原子が x 軸、 テキストボックス内の "nuc" は 各原子と 0 (= C ) 原子間の距離。
実際の H-F-H 角は 110.45°であるが、 ほぼ 正四面体の 109.45°に等しい。
そこでここでは 通常の 109.45°で計算する。
( もちろん、これらの 各原子座標を変更することができる。)
(Fig.18) 反発力を避けるために フッ素を x-y 平面上で 90°回転させる。
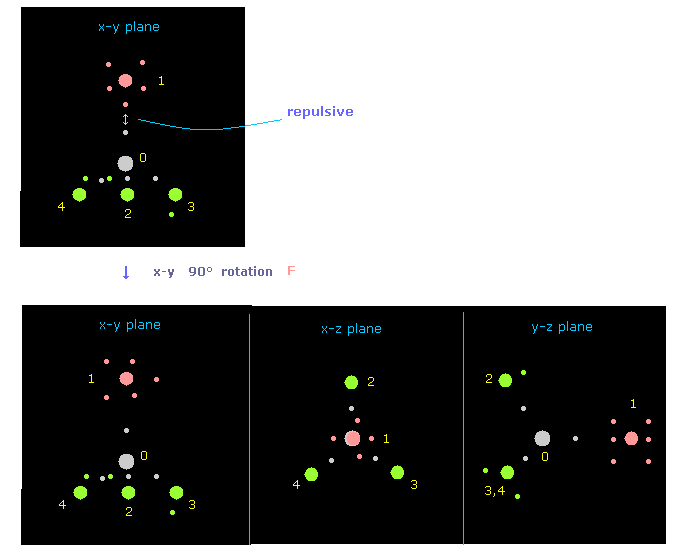
プログラム実行直後は フッ素のでっぱった価電子と 炭素の電子が 互いに近づきあっている。
そのため それらの強い反発力を避けるために、フッ素を x-y 平面上で 90°回転させる。
このページも参照のこと。
Fig.18 では "direction" ボタンをクリックして ( "1" を その隣に入力して )、atom 1 (= F ) が x 軸方向から y 軸方向へ向いている。
(Fig.19) C 原子核に作用する力が "釣り合って"いる。
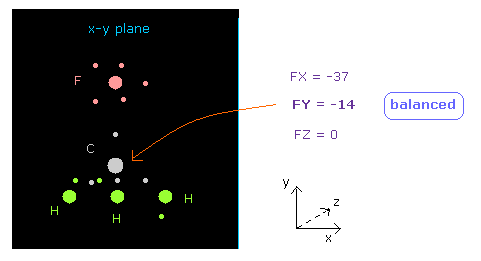
原子核画面の 下の "now 0" の行は atom 0 (= 炭素 ) に作用する力を表している。
( "now" は 現在 選択している原子の番号である。 )
FY = -14 の値は ほぼゼロである。
つまり 中心の炭素原子核に作用する力は F と 3つの H 原子の間で ちょうど 釣り合っていると言える。
"12000" の値を "atom 1" の "+Y (MM)" のところに入力して エンターキーを入力すると、 F-C の結合長は 12000 MM (= 1.2000 Å ) に変化する。
この場合は、 F 原子核による反発力のため、炭素に作用する力は ( FY = -125 ) となる。
つまり 結合長 13820 MM (= 1.3820 Å ) は それらの 釣り合いの位置から決定されていると言っていい。
(Fig.20) 4つの価電子に作用する力が "釣り合って"いる。

再び、 "13820" を "atom 1" の "+Y (MM)" のテキストボックス内に入力して、エンターキーを押す。
次に "0" を "electron" ボタンの横に入力して "electron" ボタンをクリックする。
すると 炭素原子の 4つの価電子 ( 0-3 ) が表示される。
( その周囲の 青の数字は その周囲の原子番号を意味している。 )
各電子の 力 "CF" は 各価電子に作用する力の C 原子核方向への成分である。
Fig.20 に示したように、 F-C と H-C 結合長が 1.3820 Å と 1.0950 Å のとき、これらの力は ほぼ 互いに 等しくなる。
F 側では CF = 1764、 H 側では CF = 1417 である。
(Fig.21) 4つの価電子に作用する力のバランスが壊れる。

再び "nucleus" ボタンをクリックして 原子画面に戻る。 そして +Y 座標を "13820" から "12000" にする。
これはつまり F-C 結合長が 短くなった ( 1.3820 Å → 1.2000 Å ) ことを意味している。
そして "electron" ボタンをクリック ( その隣のテキストは "0" で ) して、 炭素の価電子に作用する CF を 再び表示させる。
Fig.21 に見るように、F-C 結合長が短くなると (= 1.2000 Å )、炭素の価電子 "0" は フッ素の原子核に 引きつけられすぎることになる。
そのため CF = 356 は 他の CF = 1425 に比べて 弱くなってしまう。
( もちろん、フッ素原子核も 電子側に 強く引きつけられすぎることになる。)
これはつまり これらの粒子が CH4 のケースのように不安定になったことを意味している。
| F-C 結合長 | e0 への力 | e1 への力 | e2 への力 | e3 への力 | C 原子核への FY |
|---|---|---|---|---|---|
| 1.1500 Å | -644 | +1425 | +1428 | +1428 | -173 |
| 1.2000 Å | +356 | +1423 | +1425 | +1427 | -125 |
| 1.2500 Å | +985 | +1423 | +1425 | +1427 | -125 |
| 1.3820 Å | +1764 | +1417 | +1417 | +1422 | -14 |
| 1.4500 Å | +1935 | +1415 | +1415 | +1420 | +12 |
Table 2 に示したように、 F-C 結合長が 実験値 (= 1.3820 Å ) より短くなると、 炭素の価電子は フッ素に引かれすぎてしまい不安定になる。
F-C が 1.3820 Å のとき、 e0-e3 のすべての力は 互いに ほぼ等しくなる。
この現象は メタンと同じであり、結合長を決定する要因になる。
また C 原子核に作用する力も F-C 結合長が 1.3820 Å のとき、
釣り合っている。
( C に対する FY は ほぼ ゼロである。 )
全イオン化エネルギーは 炭素 1-4th (= 148.024 eV )、 水素 (= 13.606 eV )、 フッ素 1-7th (= 658.83 eV ) である。
このページも参照のこと。
また C-H 結合エネルギー ( 411 kJ/mol = 4.26 eV ) と C-F 結合エネルギー ( 485 kJ/mol = 5.02 eV ) を考慮すると、全エネルギーの実験値は -865.457 eV になる。
ビリアル定理を用いると、 全ポテンシャルエネルギーは 2 × -865.457 = -1730.91 eV になる。
この実験値は 上記のプログラムを用いて計算した値 (= -1731.91 eV ) とほぼ同じである。
(Fig.21') フッ素に作用する力。
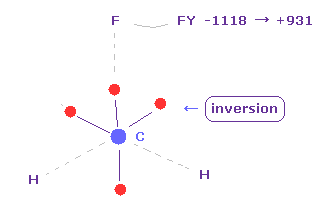
C 電子が フッ素に近づくと、 フッ素に作用する力は FY = -1118 になる。
この値は大きいように見えるが、フッ素の 大きな正電荷と 電子とその原子核間の短い距離により、フッ素の価電子を ほんの少し動かすだけで 簡単にキャンセルできる。
( 実際に フッ素の価電子のいくつかは 炭素の電子によって反発されている。試してみるといい。)
炭素の電子は 原子核周囲を周期的に回っている。
"electron" ボタンをクリック ( "0" を入力して ) して、 炭素の電子を表示させる。
そして "inversion" ボタンをクリックする。
( 4つの 炭素の電子のすべてが 原子核を挟んで逆の位置に移動する。 )
すると、炭素の電子が去った後に、フッ素の原子核は 炭素の原子核に反発される。
結果 それらの合計 (= -1118 + 931 ) は ほぼゼロになり 釣り合うことになる。
(Fig.22) C 電子に作用する力。
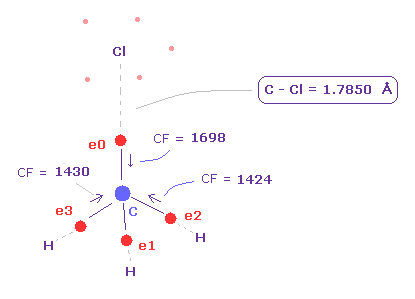
プログラムを実行後、 "methane-like = 0"、次いで "Cl-CH3 = 2" を 入力して選択する。
上記の F-CH3 と同じように、 Cl 原子を 90°回転させる。
Fig.22 に示すように、C-Cl 結合長が 実験値の 1.7850 Åのとき、 炭素の価電子に作用する力は よく釣り合っている。.
( e0, e1, e2, e3 = 1698, 1426, 1424, 1430 ).
| Cl-C 結合長 | e0 への力 | e1 への力 | e2 への力 | e3 への力 |
|---|---|---|---|---|
| 1.5500 Å | +895 | +1449 | +1447 | +1451 |
| 1.6000 Å | +1145 | +1443 | +1441 | +1446 |
| 1.6500 Å | +1343 | +1438 | +1436 | +1441 |
| 1.7850 Å | +1698 | +1426 | +1424 | +1430 |
| 1.8500 Å | +1806 | +1421 | +1419 | +1426 |
Table 3 に示したように、 Cl-C 結合長が 実験値 (= 1.7850 Å のとき、炭素の価電子に作用する力は よく釣り合っている。
他のメタン様の分子のように、Cl-C 結合長が短くなると、 C の価電子 e0 が Cl 原子核方向へ 引き寄せられ すぎて、不安定になってしまう。
------------------------------------
ここでは このページで紹介した 2原子間において 炭素の価電子に働く力を 様々な異なる結合間で比較する。
このプログラム ( もしくは そのテキスト ) を実行後、 "C" (= 炭素 ) を "A atom" として選択する。
そして 様々な原子を "B atom" として選択して、それらの 炭素の電子 "ele 0" に対する影響について調べる。
(Fig.C) 炭素 の電子に作用する力の比較。
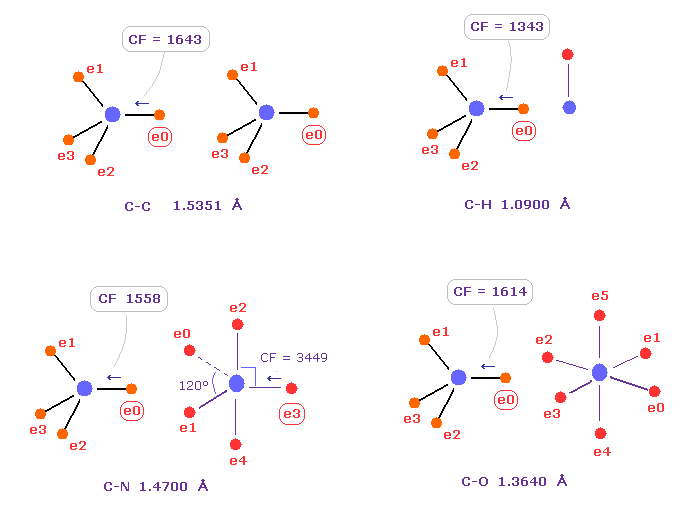
Fig.C は C-C、 C-H、 C-N、 C-O のシングル結合における 力 CFを示したものである。
炭素が 様々な結合において 正四面体構造を 保っていることを考慮すると、炭素の電子に作用する力が 互いに ほぼ 等しくなるのが自然である。
実際に これらの力 (= CF ) は 異なった C-C、C-H、C-N、C-O 結合において それぞれ 1643, 1343, 1558, 1614 になる。
( これらの結合長は 実験値である、C-O の シングル結合は 酢酸からのものである。 )
| 分子結合 | 結合長 | e0 への力 |
|---|---|---|
| C - H | 1.0900 Å | CF = 1343 |
| C - C | 1.5351 Å | CF = 1643 |
| C - N | 1.4700 Å | CF = 1558 |
| C - O | 1.3640 Å | CF = 1614 |
| C - F | 1.3500 Å | CF = 1605 |
| C - Si | 1.8500 Å | CF = 1602 |
| C - P | 1.8400 Å | CF = 1584 |
| C - S | 1.8200 Å | CF = 1708 |
| C - Cl | 1.7700 Å | CF = 1626 |
Table C は 様々な結合における 炭素の電子 "ele 0" に作用する力 (= CF ) を示したものである。
驚くべきことに、異なった結合において、これらの力 (= CF ) は ほぼ 同じになる。
これはつまり 共通のメカニズムが働いて、炭素の正四面体の構造が 様々な結合において 保たれていることを示している。
------------------------------------
全イオン化エネルギーは 1-4th (= 148.024 eV )、 水素 (= 13.606 eV )、 塩素 1-7th (= 408.88 eV ) である。
このページも参照のこと。
C-H 結合エネルギー ( 411 kJ/mol = 4.26 eV ) と C-Cl 結合エネルギー ( 327 kJ/mol = 3.39 eV ) を考慮すると、 全エネルギーの実験値は -613.89 eV となる。
ビリアル定理より、 全ポテンシャルエネルギーは 2 × -613.89 = -1227.78 eV である。
この実験値は 上記のプログラムを用いて計算した値 (= -1230.46 eV ) とほぼ同じである。
(Fig.23) 炭素原子核に作用する力。
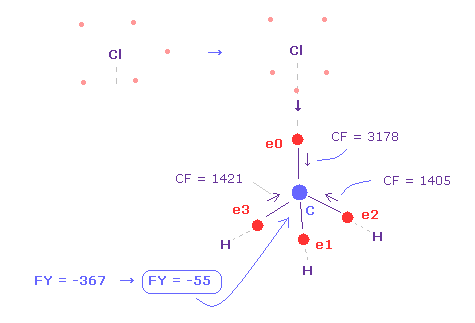
問題は 塩素の価電子は 3ドブロイ波長のために 広い範囲に分布している。
そのため そのままでは Cl 原子核が露出しているため その反発力が強くなりすぎてしまう。
実際に C 原子核に作用する力は FY = -367 となり、 これは フッ素のとき ( Fig.19 の FY = -14 ) よりも大きくなる。
広く広がっている電子のため、これらの電子は Cl 原子核に それほど強く結合していない。
( 塩素で CF=2900、フッ素で CF = 9000 である。 )
そのため 炭素の価電子が Cl に近づいているときでさえ、塩素の電子は 炭素の原子核方向を向く傾向にあると考えられる。( Fig.23 ).
この場合は、 炭素原子核に作用する力は FY = -55 になり、これは ほぼ釣り合っている。
( もちろん、この場合でさえ、これらの電子は 可能な限り 互いに避け合っていると考えられる。)
| Cl-C 結合長 | e0 への力 | C 核のFY -1 | C 核のFY-2 |
|---|---|---|---|
| 1.5500 Å | +13778 | -662 | +113 |
| 1.6000 Å | +8018 | -581 | +49 |
| 1.6500 Å | +5508 | -512 | +5 |
| 1.7850 Å | +3178 | -367 | -55 |
| 1.8500 Å | +2793 | +-313 | -66 |
Fig.23 に示したように、 Cl-C 結合長が 実験値の 1.7850 Å のとき、塩素の価電子の1つが 炭素原子核方向を向いているとき、 炭素原子核に作用する力 (= C 核 の FY-2. ) は ほぼ釣り合っている ( FY = -55 )。
この場合は、近づいた電子間の反発力のために、e0 の CF は 大きくなる(= 3178 )。
炭素電子が 原子核の逆位置にあるとき、この CF は 約 2700 ぐらいになる。
この 2700 の値と比較して、3178 の値は 受け入れられる値である。
しかし Cl-C 結合長が短くなると、C と Cl 間の反発力が 非現実的に強くなる。
( 結果的に e0 への CF は かなり大きくなる = +5508, +8018, +13778... )。
つまり これらの結合長では 炭素の電子が Cl に近づくとき、Cl の電子は C 原子核の方向を向くことができない。
結果的に Cl は 必ず Fig.22 のようになる、C 原子核に作用する 力 FY ( C 核のFY-1) は 大きくなってしまう。
よって Cl-C 結合長が 実験値より短いとき 不安定になる。
(Fig.24) フルオロフォルム (= HCF3 ) と クロロフォルム (= HCCl3 )。
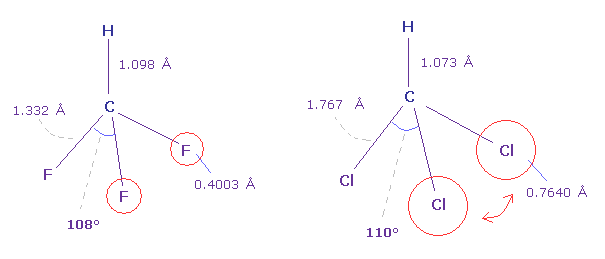
Fig.24 に示したように、フルオロフォルムの F-C-F 角 (= 108.5° ) は 基本的な 正四面体の角 (= 109.5 degree ) よりも小さい。
なぜなら 炭素原子核周囲の価電子は F 方向へ 引きつけられる傾向にあるため F 側の電子密度が小さくなるからである。
しかし クロロフォルムの Cl-C-Cl 角は Cl が 炭素よりも 強い電気陰性度を持つにも関わらず 少し大きい
(= 110.4° )。
なぜなら 塩素の7つの価電子は フッ素 (= 0.4003 Å ) よりも 広い範囲 (= 0.7640 Å ) に広がっているため、正の塩素原子核が 露出しており、強い反発力を発揮するからである。
Table 4 (= Cl ) と Table 2 (= F ) において C 原子核に作用する力 FY を比較するといい。
(Fig.25) 水 ( H2O ) の分子構造
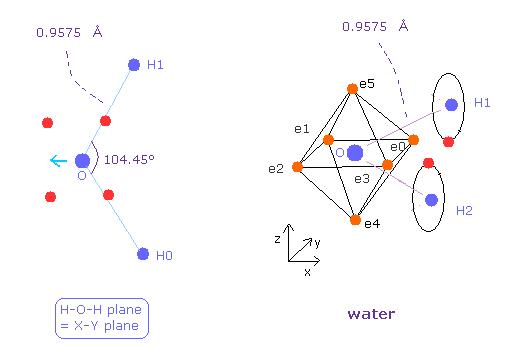
次に 水 (= H2O ) について考える。
プログラムを実行後、 H2O-like (= 1 )、 ついで H2O (= 0 ) を選択する。
H2O の酸素は メタンの炭素と異なり 非対称な配置にある。
2つの水素の正の原子核のために、酸素の電子は H の原子核のほうへ ねじれることになる。
( Fig.25 の結合長と結合核は 実験値である。 )
(Fig.26) 酸素の電子は どれだけ歪むのか?

このページに示したように、 上下の電子 (= e4, e5 ) が H 原子核方向へ 曲がるには、 e1 と e2 の電子が 外側に向かう必要がある。
( e4 と e5 の電子は 少しの動きで 酸素原子核を 水素原子核方向へ 引っ張ることができる。 )
そのため H-O-H 角は 90°(= 正八面体の角度 ) よりも 少し広くなる必要がある .
( このページでは Fig.25 の電子の番号を使う。 )
(Fig.27) 酸素 の位置の調整。
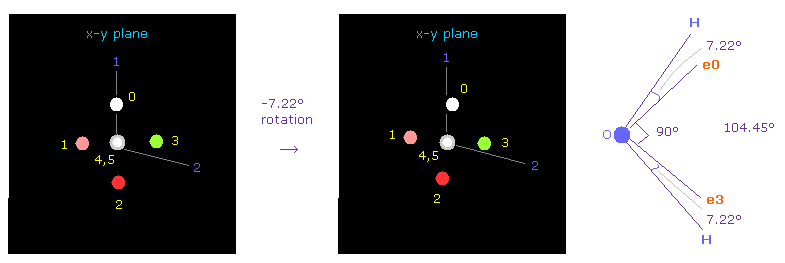
このプログラムでは、酸素の電子 0 は自動的に 初期化時に atom 1 のほうへ向く。
そのため これらの電子を atom 1 と atom 2 の両方に関して 対称的な位置に向けさせたい。
"electron" ボタンをクリック ( "0" を その横に入力して ) して 酸素の電子を表示させる。
それから x-y 平面上で それを -7.22°回転させて 2つの水素に関して 対称的な位置に向けさせる。
( "-7.22" を 指定のテキストボックス内に入力して "x-y ang" ボタンをクリックする。 )
(Fig.28) O-H 間の反発力。
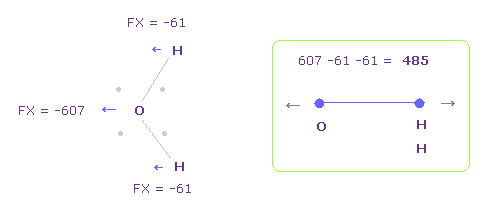
酸素の電子が どれだけ歪むかを知るために、FX 方向の全反発力を調べることにする。
Fig.28 では、 O は 左側に反発され ( FX = -607 )、2つの H は 酸素原子側に 引きよせられる ( 61 × 2 = 122 )。
そのため 全反発力は 485 になる。
水の 単一の O-H 結合エネルギーは 9.6066 eV (=926.9 kJ/mol) / 2 = 4.8033 eV である。
つまり H2O の全エネルギーは、 -433.103 (O) - 2 × 13.606 (H) - 9.6066 (結合エネルギー) = -469.92 eV となる。
ここでは 433.103 eV は 酸素の 6 つの価電子の 全イオン化エネルギーである。
ビリアル定理によれば、 全ポテンシャルエネルギー V は -939.84 eV (= 2 × E ) となる。
Fig.28 のとき、全エネルギー V は -935.14 eV となり 実験値にほぼ等しい。
(Fig.29) O-H 間の反発力 パート II.
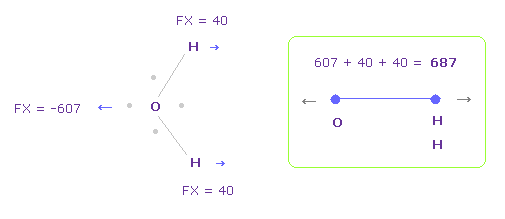
Fig.28 では、 酸素の価電子が H 原子核に 最も近づいている。
酸素の電子は 実際には軌道運動していることを考慮すると、Fig.29 のケースについても考える。
そして それらの平均の値をとる。
Fig.29 を得るには、Fig.28 から x-y 平面上で 酸素の電子を -45°回転させる。
この場合、O-H 間の全反発力は 687 になる。
(Fig.30) 平均の力。
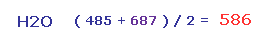
結果、 Fig.28 と Fig.29 の平均の反発力は ( 485 + 687 ) / 2 = 586 となる。
この値は 主に酸素の ゆがみによってキャンセルされる。
(Fig.31) OF2 の酸素の位置の調節。
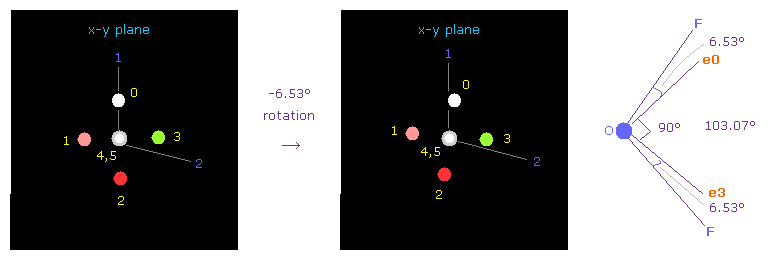
次に OF2 分子 (= 酸素 + 2つのフッ素 ) を選ぶ。
プログラムを実行後、 "1" (= H2O 様 ) を入力して 次に "1" (= OF2 ) を入力する。
F-O-F の結合角は 103.07°である。 よって 酸素の電子画面で 対称的な位置を得るために x-y 平面上で -6.53°回転させる。
(Fig.32) フッ素を 90°回転させる。
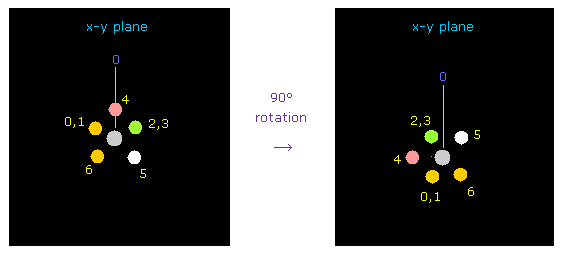
炭素とフッ素間の反発力を考慮して、2つのフッ素を x-y 平面上で 90°回転させる。
"electron" ボタンをクリックして ( テキストボックスに "1" もしくは "2" を入力した後 )、 "90" を入力して "x-y ang" ボタンをクリックする。
結果的に Fig.33 の状態を得ることができる。
( "0" を入力後 ) "nucleus" ボタンをクリックして それを確かめてほしい。
(Fig.33) OF2 における O-F 間の反発力。
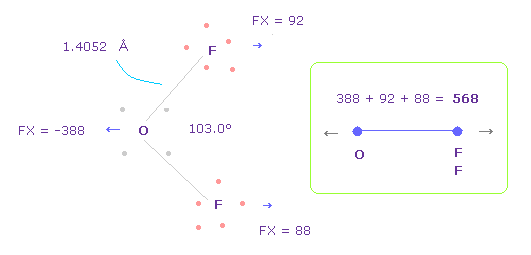
Fig.33 の結合長と角は 実験値である。
H2O のところで述べたように、酸素の価電子がどれだけ ねじれているか知るために、OF2 における 反発 FX の全量を調べることにする。
Fig.33 では、 酸素は 左側に反発され ( FX = -388 )、 2つの F も 酸素によって 反発される ( 92 + 88 = 180 )。
そのため 全反発力は 568 になる。
単一の O-F 結合エネルギーは 1.969 eV (=190 kJ/mol ) であり、これは小さい。
そのため OF2 の全エネルギーは -433.103 (O) - 2 × 658.83 (F) - 1.969 × 2 = -1754.70 eV.
ここでは 658.83 eV は フッ素の 7 つの価電子の全イオン化エネルギーである。
ビリアル定理によれば、全 V の実験値は -3509.4 eV (= 2 × E ) である。
Fig.28 では、 全 V は -3500.63 eV で、これは少し高い。
( そのため 電子の位置を少し調整する必要がある。 )
実際に O-F や F-F 結合は それらの反発力のために 非常に不安定である。
そのため フッ素は 自然界では 単独で存在できず、また O-F 結合長 (= 1.4025 Å ) は C-F 結合 (= 1.3820 Å ) よりも長い。
(Fig.34) O-F 間の反発力 パート II。
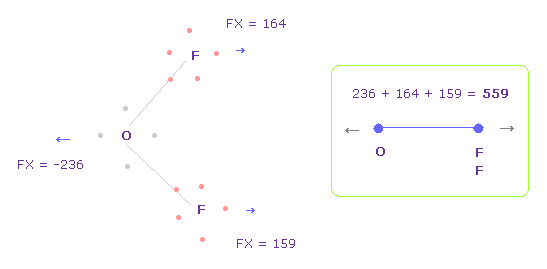
Fig.33 では、酸素の価電子は F の原子核に最も近づいている。
酸素の電子が 軌道運動していることを考慮して、Fig.34 のケースについても考える。
Fig.34 を得るには、 酸素の電子を Fig.33 から x-y 平面上で -45°回転させる。
そして ( "1" もしくは "2" を入力後 ) "electron" ボタンをクリックし、 2つの F を -90° x-y 平面で回転させて 元の状態に戻す。
このケースでは O-F 間の 全反発力は 559 になる。
(Fig.35) 平均の反発力。
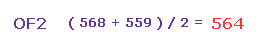
つまり Fig.33 と Fig.34 の平均の力は ( 568 + 559 ) / 2 = 563 になる。
この値は 主に 酸素のゆがみによってキャンセルされる。
また この "酸素のゆがみ" は O-H (= 586、 Fig.30 ) と O-F (= 563、 Fig.35 ) 間でほぼ同じである。
基本的に 全反発力の 1/2 は 酸素のゆがみである。
( 1/4 が H もしくは F のゆがみである。 )
このことは ある共通のメカニズムが H2O と OF2 で働いていることを意味している。
(Fig.36) OCl2 のおける 酸素の位置の調節。
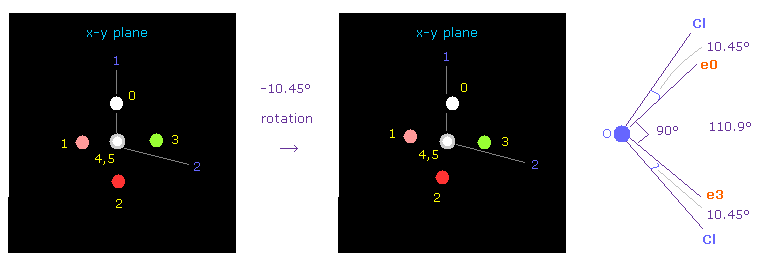
次に OCl2 分子 (= 酸素 + 2つの塩素 ) を選択する。
プログラムを実行後、 "1" (= H2O like )、次いで "2" (= OCl2 ) を入力する。
Cl-O-Cl の結合角は 110.9°であるため、 酸素の電子画面で 対称的な位置を得るために x-y 平面上で -10.45°回転させる。
Fig.23 で述べたように、塩素の価電子は 広く分布しているため Cl の原子核が露出している。
O-Cl 間の長い結合距離などを考慮すると、Cl 電子の1つが ほぼ 常に O 原子核の方向へ向いていると仮定できる。
(Fig.37) OCl2 の O-Cl 間の反発力。
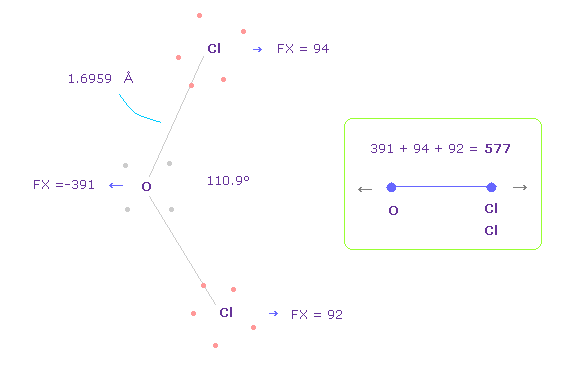
Fig.37 の結合長と結合角は 実験値である。
H2O のところで述べたように、酸素の価電子がどれだけ ねじれるのか知るために、OCl2 における FX の全反発力を調べる。
Fig.37 では、 O は 左側に反発され ( FX = -391 )、 2つの Cl も 酸素によって反発される ( 94 + 92 = 186 )。
そのため 全反発力は 577 になる。
(Fig.38) O-Cl 間の反発力、 パート II。
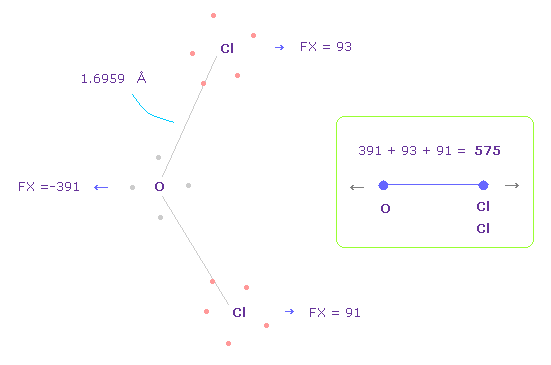
Fig.37 では、酸素の価電子は Cl 原子核に近付いている。
酸素の電子が 軌道運動していると考えて、 Fig.38 のケースについても考える。
Fig.38 を得るために、酸素の電子を Fig.37 から -45°、x-y 平面上で回転させる。
このケースでは、O-Cl 間の全反発力は 575 になる。
(Fig.39) 平均の反発力。
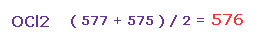
そのため Fig.37 と Fig.38 の平均の反発力は ( 577 + 575 ) / 2 = 576 となる。
この値は 主に酸素のねじれによってキャンセルされると考えられる。
また このねじれ具合は O-H (= 586、Fig.30 ) や O-F (= 563、 Fig.35 ) のケースとほぼ同じである。
結果的に 酸素のねじれの観点から H2O、 OF2、 OCl2 において 共通の結果を得ることができた。
( H2O、OF2、OCl2 で それぞれ 586、 563、 576 である。 )
2つの塩素の反発力は 最も強い ( Cl と F における FY を比較すると分かる。)
そのため Cl-O-Cl 結合角は それらで最も大きくなる。
| O-H 結合長 | 反発力-1 | 反発力-2 | 平均の力 |
|---|---|---|---|
| 0.8500 Å | 598 | 1024 | 811 |
| 0.9000 Å | 541 | 845 | 693 |
| 0.9575 Å | 485 | 687 | 586 |
| 1.0000 Å | 441 | 593 | 517 |
ここで O-H 結合長と 反発力の関係について調べる。
O-H 結合長を変化させるには、"direction" ボタンを用いて 1 もしくは 2 を y 軸方向へ向けさせて その Y 座標を したい結合長の値に変更すればいい。
Table 5 に示したように、水の O-H 結合長が 実験値の 0.9757 Å のとき、反発力の値 586 は OF2、OCl2 の 563 と 576 にほぼ等しくなる。
これはつまり 様々な分子において 共通のメカニズムが働いていることを意味している。
(Fig.40) OFH における 酸素の位置の調節。
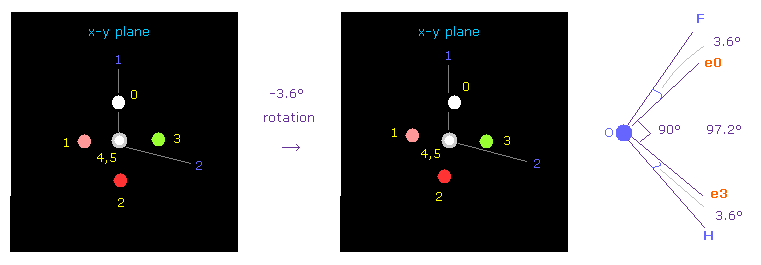
次に OFH 分子 (= 酸素 + フッ素 + 水素 ) について調べる。
プログラムを実行後、 "1" (= H2O like )、次いで "3" (= OF2 ) を入力する。
F-O-H の結合角は 97.2° である。よって 酸素の電子画面で -3.6° x-y 平面で回転させ 対称的な位置を得る。
(Fig.41) フッ素を -90°回転させる。
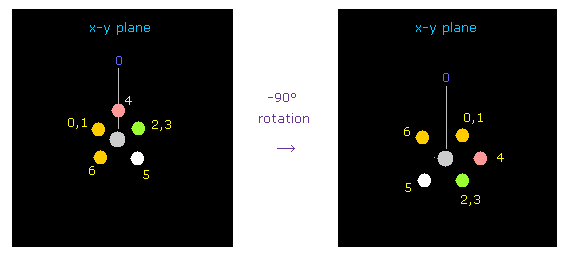
炭素とフッ素の反発力を考慮して、フッ素を -90°、x-y 平面上で回転させる。
"1" をテキストボックス内に入力後、 "electron" ボタンをクリックし、次いで "-90" を入力後、 "x-y ang" ボタンをクリックする。
( ここでは -90°回転のほうが 90°回転よりも 酸素の原子核が安定化する。 )
結果的に Fig.42 の状態を得ることができた。
"0" を入力後 "nucleus" ボタンをクリックして それを確かめてほしい。
(Fig.42) OFH における O-F,H 間の反発力。
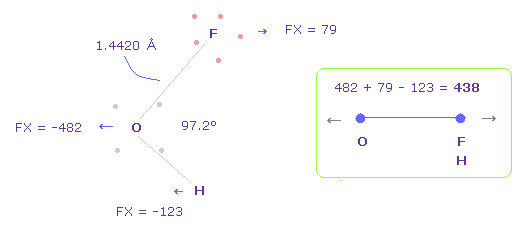
Fig.42 の結合長と結合角は 実験値である。
Fig.42 では、 O は 左側に反発され ( FX = -482 )、 F も 酸素によって反発され、 ( FX = 79 ).
H は 酸素に引きつけられる ( FX = -123 )。
そのため 全反発力は 482 + 79 - 123 = 438 になる。
単一の O-F、 O-H 結合エネルギーは 1.969 eV (=190 kJ/mol )、 4.75 eV (= 459 kj/mol) である。
そのため OFH の全エネルギー は -433.103 (O) - 658.83 (F) - 1.969 - 4.75 = -1098.65 eV. である。
ここで 658.83 eV は フッ素の 7つの価電子の 全イオン化エネルギーである。
ビリアル定理によれば、 全 V の実験値は -2197.30 eV (= 2 × E ) である。
Fig.42 では、 全 V は -2217.88 eV で それは少し 低くなる。
(Fig.43) F と H が 互いに引き合っている。
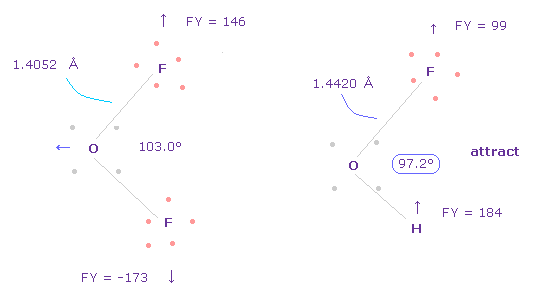
なぜなら 水素とフッ素は 互いに 引き合っているからである。
そのため この F-H の結合エネルギーも考慮する必要がある。
また 2つのフッ素は 互いに反発している。
実際に F-O-F の角度は F-O-H 角よりも広い。力 FY を見れば この事実が理解できる。
(Fig.44) O-F,H 間の反発力、 パート II。
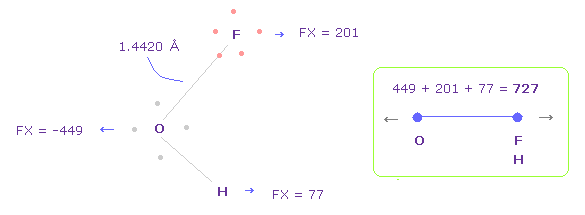
Fig.42 では、酸素の価電子は F の原子核に最も近づいている。
酸素の電子が 軌道運動していることを考慮して、Fig.44 のケースについても考える。
Fig.44 を得るには 酸素の電子を x-y 平面で Fig.42 の状態から -45° 回転させる。
そして "1" を入力後、 "electron" ボタンをクリックして 2つの F を x-y 平面上で 90°回転させ 元の状態に戻す。
このケースでは、O-F,H 間の全反発力は 727 になる。
(Fig.45) 平均の力。
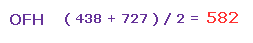
よって Fig.42 と Fig.44 の平均の力は ( 438 + 727 ) / 2 = 582 となる。
また この値は 妥当な値である。なぜなら それはちょうど H2O (= 586、 Fig.30 ) と OF2 (= 563、 Fig.35 ) の間だからである。
| 分子 : | H2O | OF2 | OCl2 | OFH |
|---|---|---|---|---|
| 反発力: | 586 | 564 | 576 | 582 |
結果的に 全反発力 (= 酸素のねじれ ) の視点から H2O, OF2, OCl2, OFH などの様々な H2O 様の分子で 共通のメカニズムが 働いていることが Table 6 から判断できる。
OClH のケースについても試してみると言い。
ポイントは 上で述べたように Cl の原子核は 強い反発力を持ち、かつ 長い O-Cl 結合長を考慮すると Cl 電子の1つは 常に酸素原子核の方向へ 向く傾向にあるということである。
(Fig.46) フォルムアルデヒド ( O=CH2 )。
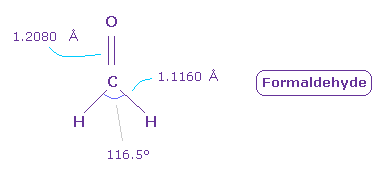
次に フォルムアルデヒド ( O=CH2 ) について考える。
C=O の 2重結合長 は 1.2080 Å で、H-C 結合長は 1.1160 Å である。
また H-C-H 角は 116.5°である。
プログラム実行後 "2" (= formaldehyde like ) を入力して、 "0" ( O=CH2 ) を入力して、エンターキーを押す。
(Fig.47) y-z 平面で C を -54.73°回転させる。
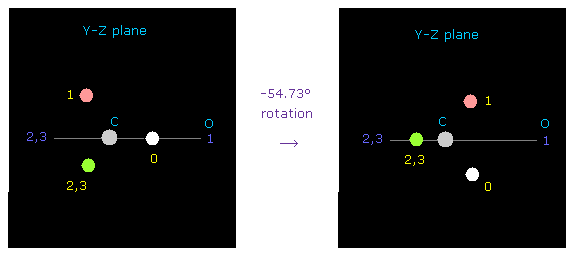
初期化時には 炭素の価電子 "e0" は atom 1 (= 酸素 ) の方を向いている。
2重結合を表すには、 y-z 平面で 炭素を -54.73°回転させる。
( "0" を入力し、 "electron" ボタンをクリックし、 -54.73 を入力し、"y-z ang" ボタンをクリックする。 )
(Fig.48) x-y 平面上で 酸素を -45°回転させる。

酸素サイドでも 2重結合を表すのに x-y 平面上で -45°回転させる。
( "1" を入力して "electron" ボタンをクリックし、 -45 を入力して "x-y ang" ボタンをクリックする。 )
(Fig.49) C 原子核に作用する力。
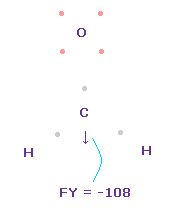
この状態では 炭素原子核 ( atom 0 ) に作用する力は FY = -108 となり ほぼゼロである。
Fig.49 では、 H-O-H は 実験値の 116.5°であるが、それに対応する 炭素の電子 e2-C-e3 の角度は 元の 109.45°のままである。
(Fig.50) 炭素の電子の角度を 109.45°から 116.5°に広げる。
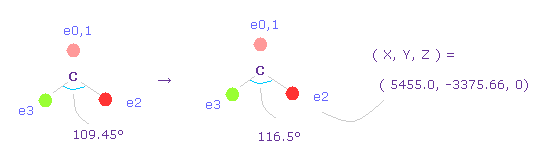
2つの水素原子の引きつけ力を考慮して、炭素の価電子間の角度を 109.45°から 116.5°に広げる。
"0" を入力して "electron" ボタンをクリックし、座標 ( 5455.0, -3375.66, 0 ) の値を ele 2 のテキストボックスに入力する。
ele 3 には ( -5455.0, -3375.66, 0 ) を入力して エンターキーを押す。
(Fig.51) C 原子核への力。
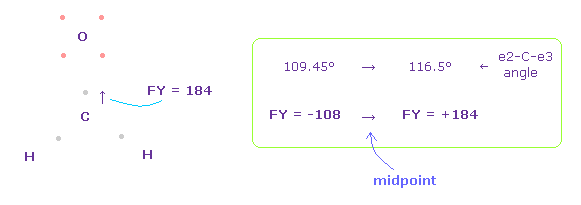
この場合では、炭素原子核に作用する力は FY = +184 になる。
結果的に 炭素の2つの電子は 2つの水素原子核に少し引きつけられ、 e2-C-e3 の角度は C 原子核を安定にするため 元の 109.45°と 116.5°の間になる。
つまり この 古典的な軌道は フォルムアルデヒドにおいても 核の安定性を説明することができた。
(Fig.52) 酸素原子核に作用する力。
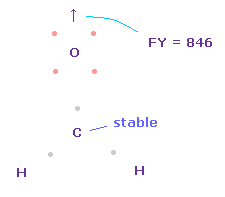
炭素に作用する力は その電子間の角度が 2つの水素原子核に引かれて 少し広くなると ゼロになる。
問題は 炭素原子核の酸素に対する反発力が そのままでは強すぎる ( FY = 846 ) 点である。
(Fig.53) 炭素の電子の回転。
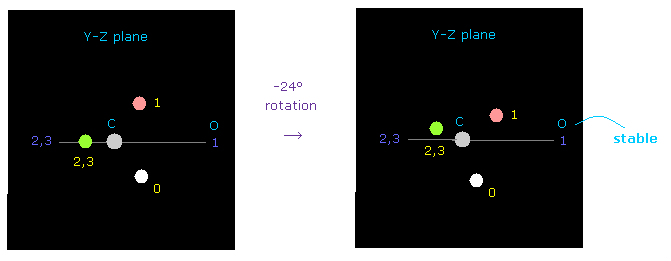
しかし 炭素の価電子を y-z 平面上で -24°ほど少し傾けると 酸素原子核に対する反発力は 容易にキャンセルできる。
酸素の電気陰性度は 炭素よりも 強く、また それらの電子の回転周期は 異なる、
これらの事実を考慮すると、炭素の電子の1つが C=O の2重結合においても 酸素のほうへ
しばしば引きつけられていると考えるのが妥当である。
( おそらく、実際の回転角度は 酸素のねじれを考慮すると 0 から -24°の間であろうと考えられる。)
(Fig.54) O=CF2 分子。
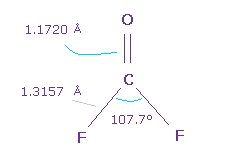
次に O=CF2 について考える。
C=O の 2重結合長 は 1.1720 Å で、F-C 結合長は 1.3157 Å である。
また H-C-H 角は 107.7°であり、これは少し小さい。
なぜなら F の強い電気陰性度のために 炭素の電子は F 側へ引きつけられる傾向にあり、F 側の電子密度が 薄くなるからでる。
プログラム実行後 "2" (= formaldehyde like ) を入力して、 "1" ( O=CF2 ) を入力して、エンターキーを押す。
(Fig.55) y-z 平面で C を -54.73°回転させる。

初期化時には 炭素の価電子 "e0" は atom 1 (= 酸素 ) の方を向いている。
2重結合を表すには、 y-z 平面で 炭素を -54.73°回転させる。
( "0" を入力し、 "electron" ボタンをクリックし、 -54.73 を入力し、"y-z ang" ボタンをクリックする。 )
(Fig.56) x-y 平面上で 酸素を -45°回転させる。

酸素サイドでも 2重結合を表すのに x-y 平面上で -45°回転させる。
( "1" を入力して "electron" ボタンをクリックし、 -45 を入力して "x-y ang" ボタンをクリックする。 )
(Fig.57) フッ素を 90°回転させる。

炭素とフッ素の電子間の反発力を考慮して フッ素を x-y 平面上で 90°回転させる。
テキストボックス内に "2" と "3" を入力して "electron" ボタンをクリックし、 "90" を入力して "x-y ang" ボタンをクリックする。
(Fig.58) C 原子核に作用する力。
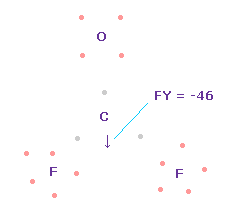
この状態では 炭素原子核 ( atom 0 ) に作用する力は FY = -46 となり ほぼゼロである。
Fig.58 では、 F-O-F は 実験値の 107.7°であるが、それに対応する 炭素の電子 e2-C-e3 の角度は 元の 109.45°のままである。
(Fig.59) 炭素の電子の角度を 109.45°から 107.7°に狭める。
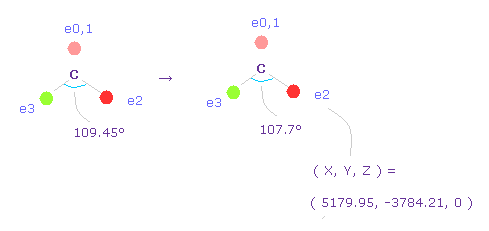
2つのフッ素原子の引きつけ力を考慮して、炭素の価電子間の角度を 109.45°から 107.7°に狭める。
"0" を入力して "electron" ボタンをクリックし、座標 ( 5179.95, -3784.21, 0 ) の値を ele 2 のテキストボックスに入力する。
ele 3 には ( -5179.95, -3784.21, 0 ) を入力して エンターキーを押す。
(Fig.60) C 原子核への力。
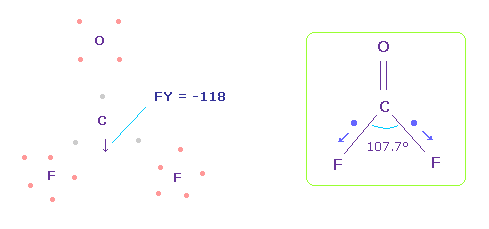
この場合では、炭素原子核に作用する力は FY = -118 になる。
これは ほぼゼロであるが、Fig.58 よりも よりフッ素側に引きつけられている。
この差は フッ素の 非常に強い電気陰性度を無視したことにある。
基本的に 炭素の電子は F 側に強く引きつけられて 炭素から離れる傾向にある。
結果的に F 側の電子密度 は減少して 結合角は狭くなる。
そのため この FY = -118 は 去っていく電子のために キャンセルされて C 原子核は 安定になる。
(Fig.61) O=CCl2 分子。
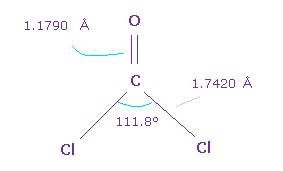
次に O=CCl2 について考える。
C=O の 2重結合長 は 1.1790 Å で、Cl-C 結合長は 1.7420 Å である。
また Cl-C-CL 角は 111.8°であり、これは F-C-F 角よりも広い。
なぜなら Cl-Cl 原子核間の反発力が F-F 間よりも強いからである。
Fig.44 と同様のメカニズムで、H は 酸素側へ引きつけられる傾向にあり、Cl と F は 酸素に 反発される。
そのため H-C-H 角 (= 116.5°) は Cl-C-Cl 角 (= 111.8°) よりも広い。
プログラム実行後 "2" (= formaldehyde like ) を入力して、 "2" ( O=CCl2 ) 入力して、エンターキーを押す。
(Fig.62) C 原子核に作用する力。
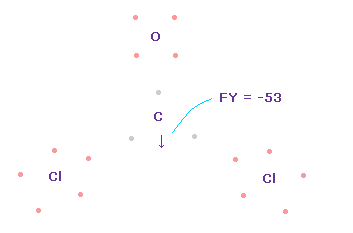
Fig.55 や Fig.56 と同様に、2重結合を形成するために 酸素や炭素の電子を回転させる。
また Cl-CH3 や OCl2 分子 のところで説明したように、Cl 電子の1つは 長い Cl-C 結合長のために いつも C 原子核方向へ向く傾向にあると仮定する。
この状態では 炭素原子核 ( atom 0 ) に作用する力は FY = -53 となり ほぼゼロである。
Fig.62 では、 Cl-O-Cl は 実験値の 111.8°であるが、それに対応する 炭素の電子 e2-C-e3 の角度は 元の 109.45°のままである。
(Fig.63) 炭素の電子の角度を 109.45°から 111.8°に狭める。
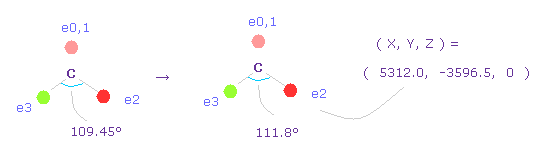
2つの塩素原子の引きつけ力を考慮して、炭素の価電子間の角度を 109.45°から 111.8°に広げる。
"0" を入力して "electron" ボタンをクリックし、座標 ( 5312.0, -3596.5, 0 ) の値を ele 2 のテキストボックスに入力する。
ele 3 には ( -5312.0, -3596.5, 0 ) を入力して エンターキーを押す。
(Fig.64) C 原子核への力。
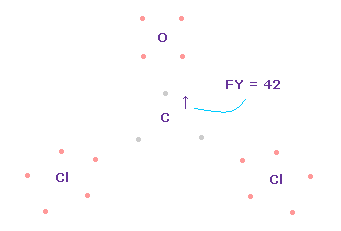
この場合では、炭素原子核に作用する力は FY = +42 になる。
これは ほぼゼロで いい値である。
フォルムアルデヒドのケースのように、O=CCl2 分子においても、e2-C-e3 角は 109.45°と 111.8°の間のときに、炭素原子核に作用する全力は ゼロになり 安定する。
このプログラムは 様々なもっと大きい分子を扱える。
詳細な方法に関しては このページを参照のこと。

2013/5/12 updated This site is link free.