操作方法

　平均 E(X)：
　　　　平均（期待値）をタイプしてください。
　　　　対数変換後の平均μ ではありません。
　　　　参考 : 対数変換後の平均μ = ln{E(x)} - σ²/2

　対数変換後標準偏差σ：
　　　　対数変換後の標準偏差でタイプして下さい。
　　　　平均が500で、±50程度ばらつく可能性が68%なら
　　　　50/500 つまり 0.1 をタイプするという感じですが、
　　　　まあ・・・これは、ラフでアバウトな説明でして・・・
　　　　とにかく、対数変換後の標準偏差をタイプして下さい。
　　　　
　モンテカルロ法：
　　　　標準版、改良版のいずれかを選択してください。
　　　　標準版選択時
　　　　　１個目〜100個目のいずれも、一様乱数[0,1]を発生させて計算
　　　　改良版選択時
　　　　　１個目 ：一様乱数[0 ,0.01]を発生させて計算
　　　　　２個目 ：一様乱数[0.01 ,0.02]を発生させて計算
　　　　　３個目 ：一様乱数[0.02 ,0.03]を発生させて計算
　　　　　・・・・・・・
　　　　　100個目：一様乱数[0.99 ,1 ]を発生させて計算
　　　　　
　　　　改良版を選択では、結果出力の平均と入力の平均 E(X)との
　　　　差異が少ない結果出力となる。
　　　　
　計算：クリックとすると計算結果を表示します。

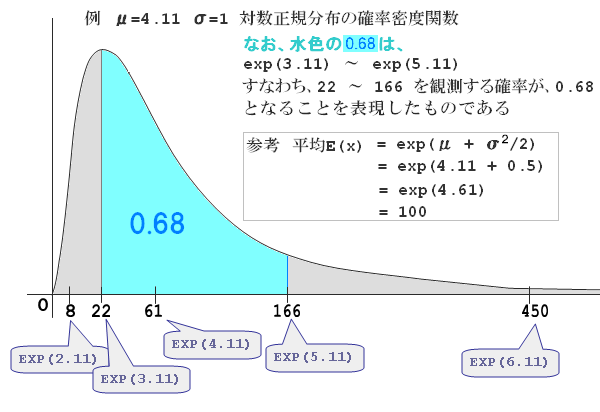
対数正規分布のイメージ

処理ロジック概要（モンテカルロ法 : 標準版）

　　1)　ex ← 平均
　　2)　sigma ← 対数変換後標準偏差
　　3)　mu ← Math.Log(ex) - Math.pow(sigma,2) / 2
　　4)　100回繰り返す
　　　　　p ← [0,1]の一様乱数
　　　　　ld(*) ← F_LOGINV(p,mu,sigma)
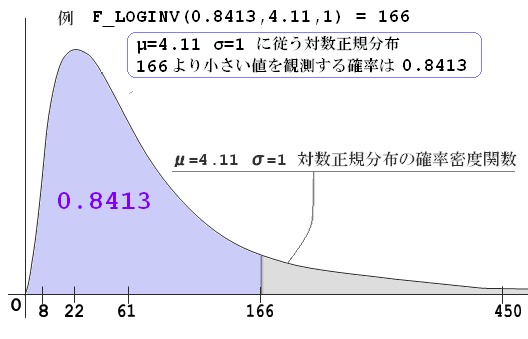
　　　　　補足: F_LOGINV は、対数正規分布の累積分布関数の逆関数（自作）
　　　　　補足: F_LOGINV のイメージ
　　5) ld(*) をソートして表示

処理ロジック概要（モンテカルロ法 : 改良版）

　　1)　ex ← 平均
　　2)　sigma ← 対数変換後標準偏差
　　3)　mu ← Math.Log(ex) - Math.pow(sigma,2) / 2
　　4)　100回繰り返す
　　　　・１回目 p ← [0.00 , 0.01]の一様乱数
　　　　・２回目 p ← [0.01 , 0.02]の一様乱数
　　　　・３回目 p ← [0.02 , 0.03]の一様乱数
　　　　・・・・・・・・・・・・・・・・・
　　　　・ｎ回目 p ← [0.01・(n-1) , 0.01・n ]の一様乱数
　　　　・・・・・・・・・・・・・・・・・
　　　　・ 99回目 p ← [0.98 , 0.99]の一様乱数
　　　　・100回目 p ← [0.99 , 1.00]の一様乱数
　　　　
　　　　ld(*) ← F_LOGINV(p,mu,sigma)
　　　　補足: F_LOGINV は、対数正規分布の累積分布関数の逆関数（自作）
　　　　
　　5) ld(*) 表示

| TOP | | 前へ |