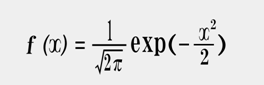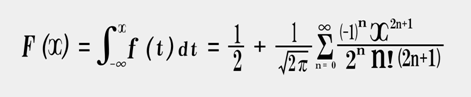全体概要
1) 標準正規分布の累積分布関数の逆関数 を自作
2) 下記の10点を画面に表示
・平均 + F_NORMSINV(0.05) × 標準偏差
・平均 + F_NORMSINV(0.15) × 標準偏差
・平均 + F_NORMSINV(0.25) × 標準偏差
・平均 + F_NORMSINV(0.35) × 標準偏差
・平均 + F_NORMSINV(0.45) × 標準偏差
・平均 + F_NORMSINV(0.55) × 標準偏差
・平均 + F_NORMSINV(0.65) × 標準偏差
・平均 + F_NORMSINV(0.75) × 標準偏差
・平均 + F_NORMSINV(0.85) × 標準偏差
・平均 + F_NORMSINV(0.95) × 標準偏差
F_NORMSINV : 標準正規分布の累積分布関数の逆関数(自作)
標準正規分布の累積分布関数の逆関数
自作関数名 : F_NORMSINV
引数 : 確率
返却値: この返却値より小さくなる値を観測する確率が引数となる
実現方法:標準正規分布の累積分布関数 F_NORMSDISTを自作し
F_NORMSDIST が引数(確率)に、ほぼ等しくなるように
バイナリーサーチ的な方法で、50回反復し求める
イメージ:
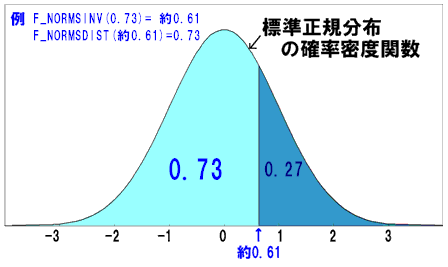
標準正規分布の累積分布関数
自作関数名 : F_NORMSDIST
引数 : 値
返却値 : 引数の値以下となる確率
実現方法:
・ ±3σ範囲内
標準正規分布の確率密度関数
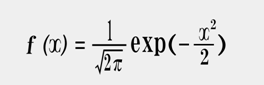
これの累積分布関数ならびに、そのマクローリン展開した数式は、
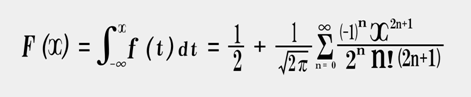
となる。
∑の部分は、n = 0~31 までの合算し、算出
・ ±3σ範囲外 (かつ±12σ範囲内)
マクローリン展開式では、σが0から離れるに従い収束が
急速に悪くなる。
またnを極めて大きくとっても、桁落ち誤差が発生するため、
精度がよくない。
というわけで、適当な区間に分けて、小生考案の近似式で補間した。
おそらく、有効数字は、3桁ぐらいかと
・ (±12σ範囲外)
σ>12 なら 1 σ<-12なら 0 を返却します。
厳密には、ジャスト0とかジャスト1ではないが、
その誤差は天文学的に小さい。・・・よね。