Home page
Einstein is wrong
Twin paradox is real
(Fig.1) A very long stick K' starts to accelerate at the acceleration of α at time t = t' = 0 in the right direction with respect to the stationary K observer. Unreal black hole going back to the past appears only when seen by K' !?

In the upper Fig.1, a long stick K' starts to accelerate at the time t = t' = 0 at the acceleration of α in the right direction.
↑ So the this stick K' position moves to x = 1/2αt2 at the time t, as seen by the stationary observer K (= inertial or lab frame with no acceleration ).
When seen by this accelerating stick K' (or an accelerating observer moving with the stick K' = accelerating frame ), all things in the K inertial frame appear to be accelerating in the opposite direction.
According to Einstein relativity, the artificial gravitational time dilation is caused when seen by the accelerating stick (= called uniform-accelerating Rindler coordinate, this-lower ), because it is as if all things in K are accelerating in the opposite direction by the fake gravitational force as seen by the accelerating observer K'.
↑ Einstein equivalence principle says ( fictional ) gravitational time dilation is caused also when seen by an accelerating observer who sees pseudo-gravitational time dilation or Rindler's pseudo-black hole event horizon where time stops ( this-p.26-32, this-p.2-2.2, p.3-footnote ).
The problem is Einstein relativity says the paradoxical black hole called Rindler horizon beyond which the clock time unrealistically runs backward to the past (= t < 0 ) must suddenly appear only when seen by the accelerating stick K' ( this-2nd-paragraph, this-middle, this-p.28-39 ), which disproves Einstein relativity.
The time (= t' ) and space (= x' ) measured by the uniformly accelerating stick K' is called Rindler coordinate ( this-p.5-(8), this-p.4 ).
↑ In this accelerating Rindler frame, the time (= t ) of clocks in the inertial frame K unrealistically goes back to the past ( t < 0 ) in the place of x' < -c2/α or x < -c2/α (= x is equal to x' at the time of t = t' = 0 ).
So as seen by the accelerating stick K', all information or signals from the places of x < -c2/α unrealistically can Not be known nor reach other places of x > -c2/α, as if the artificial (unreal) black hole ( Rindler ) horizon suddenly appears at the place of x = -c2/α ( this-p.2-3rd-paragraph, this-p.11-lower~p.12 ).
This-p.3-last~p.4-3rd-paragraph say
"The coordinate system of B, during the accelerating phase cannot be an inertial
reference frame. We consider the transformation of coordinates between (T, X)
for twin A and (T˜ X˜) for twin B"
"hence twin B sees twin A as moving in the negative X˜ direction, but as far as twin B is concerned, twin A never manages to move past −1/g (= =- c2/α = Rindler pseudo-black hole horizon ) as T˜ → ∞ (= no matter how much time passes ). This boundary is a coordinate artefact known as the Rindler horizon or edge of the Rindler wedge"
↑ This causes irreparable paradox including twin paradox that needs the explanation of accelerating observers' clock time disproving Einstein relativity.
(Fig.2) Light can Not be emitted at time t = 1 from the position of x < -c2/α only when seen by accelerating K' stick (= but when seen by K frame, the same light is emitted at t = 1 and overtakes the stick and reaches detectors ), which is clearly paradox.

In the upper Fig.2, the light is emitted from the positions of x < -c2/α at the time of t = 1, which light traveling at the light speed c can overtake and reach detectors attached to any positions ( x or x' > -c2/α ) of the accelerating stick K' (= moving slower than the light speed c ) as seen by the stationary observer in the inertial frame K (= when this K' detector passes K, the stationary K observer can confirm this detector already detected the light ).
But according to the paradoxical Einstein relativity, only when seen by the accelerating stick K', the artificial black hole ( Rindler ) horizon suddenly appears, and all clocks in the places of x < -c2/α (= x' < -c2/α ) unrealistically go back to the past (= always t < 0 ), so the light is Not emitted at t = 1.
↑ Light detected as seen by K cannot be detected as seen by the accelerating stick K', which is clearly paradox, disproving Einstein relativity ( this-p.10-horizon, this-p.12-lower ).
↑ As seen by the stationary K, K can confirm the accelerating K's detector already detected the light emitted from x' < -c2/α at time t = 1, when K' detector passes K.
But as seen by the accelerating K', the same light can never be emitted from x' < -c2/α due to (unreal) Rindler black hole whose time goes back to the past ( t < 0 ), so when K' detector passes the stationary K, K' detector still can not detect the light, which is clearly relativistic paradox, and Einstein relativity is wrong.
This ( or this )-middle-Horizons and Rindler wedges say
"For a uniformly accelerating observer, there exists a Rindler horizon, which is a boundary beyond which the observer can neither see nor influence any events. This concept is analogous to the event horizon of a black hole."
This-p.9-left-last says
"This boundary is called the horizon or edge of the
Rindler wedge, the accelerated observer cannot see the whole of the Minkowski (= inertial ) spacetime (= cannot detect light signal emitted from places beyond the unreal Rindler black hole that paradoxically does not appear only when seen by stationary K )"
↑ As shown here, Einstein relativity shows fatal paradox where clocks tick at the same or different paces as seen by different (= stationary or accelerating ) observers.
(Fig.3) Relativistic accelerated Rindler coordinate transformation is unreal.
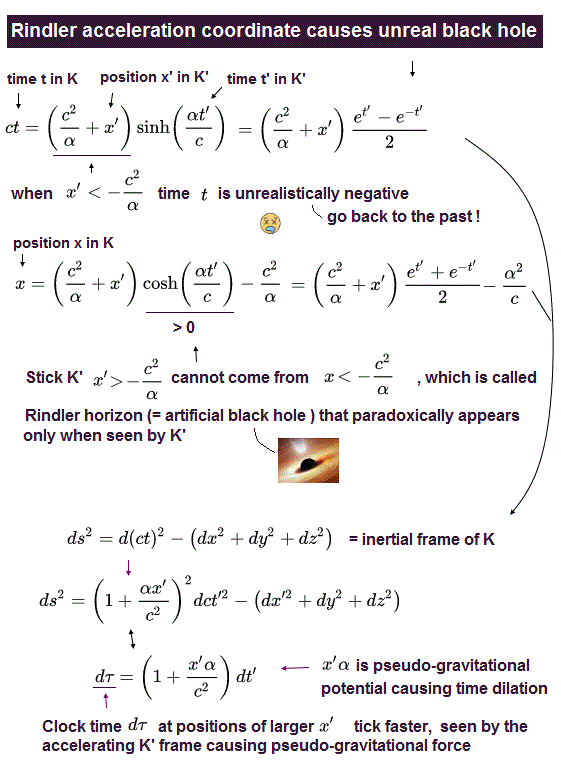
When the stick K' is uniformly accelerating at the acceleration of α seen by the stationary observer K (= inertial frame ), the relation between the time (= t ) space (= x ) of K frame and the time (= t' ) space (= x' ) of K' is given by Rindler coordinate ( this-p.5-(8), this-p.8, this-p.4 ), according to Einstein general relativity.
This-p.4-5th-paragraph (+ p.5-(15) ) says
"Now, similar to when we derived the Lorentz transformations, we want to
find an expression which relates the time and space coordinates of the inertial
observer (= stationary K ), T (= t ) and X (= x ), to the time and space coordinates that the accelerated
observer (= accelerating stick K' ) would use, which we will refer to as η (= time t' seen by K' ) and ξ (= position x' seen by K' )"
In this unphysical Einstein relativity, only when seen by the accelerating observer or stick K', the artificial black hole (= Rindler horizon ) suddenly appears, and prohibits us from entering the places of x < -c2/α ( this-p.39,p.42, this-p.1-left, p.2-left-1st-paragraph, this-p.11-lower~p.12 ).
↑ This causes serious paradox such as irreparable twin paradox ( this-p.4, this-p.2-last, ) disproving Einstein relativity.
Inserting this accelerating Rindler coordinate into the inertial frame equation can get the time dilation equation under the artificial gravitational acceleration of α ( this-p.3-V~p.4, this-p.3-right-p.4, this-p.4 ).
In the places of larger x' (= or larger x ), the clock time t runs faster with respect to the same interval of the time t' due to the fake gravitational (= acceleration ) time dilation ( so light speed can exceed c in larger x places, this-p.11-(70) ), only when seen by the accelerating stick K'.
In the places of smaller x' (= or smaller x ), the clock time t runs slower, and in places of x' (= or x ) < -c2/α, the unreal Rindler black hole appears, only when seen by the accelerating stick K' causing paradoxes.
(Fig.4) General relativistic accelerated frame (= Rindler coordinate ) needs to unrealistically expand a rigid stick K' to infinite length.

The rigid stick K' is uniformly accelerating at the acceleration of α with respect to the stationary observer in the inertial frame K.
According to the Einstein relativity, this rigid stick seen by the accelerating stick K' itself paradoxically appears to be expanding (= Einstein is wrong, disobeying the fact that the rigid body cannot be expanded just by the simple acceleration ) due to Rindler accelerating coordinate.
In this uniform accelerating Rindler frame, all parts of x' < -c2/α (= x < -c2/α ) of the stick unrealistically appear to go back to the past ( t < 0 ), and move back in the negative x direction as the time t' passes.
All other parts x' > -c2/α (= x > -c2/α ) in the stick move forward in the positive x direction, which means the rigid stick is unrealistically expanding in both ±x directions only when seen by the accelerating stick K'.
The positional relationship of x' = x = -c2/α is unchanged (= only this point of the stick unrealistically remains still forever ) no matter how much K' time t' passes, because K time t remains 0 in this position.
↑ This same rigid stick's length remains the same as seen by the stationary observer in the inertial frame K, so this is clearly paradox called Bell spaceship paradox disproving Einstein relativity.

Feel free to link to this site.