(Fig.1) ↓ A photon or very weak light is too easily lost. which makes it impossible to scale up photon or optical quantum computer.
Despite extremely long years of researches, the overhyped quantum computers (= still Not computers ) are still useless (= except for research or hype purpose ), which fact proves quantum computers are hopeless and deadend forever.
Only overhyped empty promises inundate the (already-dead) quantum computer's news ( this key takeaway, this 1~2nd-paragraphs ).
Photon or optical quantum computers using weak classical light or a photon's state as a qubit 0 or 1 that are easily lost, are one of the most overhyped hopeless useless technologies.
This p.1-left-2nd-paragraph says
"However, as in other experimental platforms, one of the
main obstacles to implementing a large-scale quantum
device to perform interesting quantum information
processing is noise; especially, photon loss"
This-middle-photonic quantum computers-weakness-include says
"Error Correction: Building an effective error correction system for photons is challenging (= correcting errors of the current error-prone photon quantum computers is impossible )."
"Loss and Noise: Photonic systems can suffer from loss and noise that impact the fidelity of the operations (= photons or very weak light are easily lost, impractical, causing many errors)."
"Challenging gate operations: Implementing logic gates on light particles is complex and resource-intensive (= qubit gate operation of photon quantum computers is impossible )."
"Limited controllability: Addressing and manipulating individual photons presents significant difficulties (= manipulating fragile photons is impractical )."
The most-often-seen hype (= always avoiding mentioning massive photon's loss ) is "photonic quantum computers may have advantage of operating at room temperature", which is a lie.
This 7th-paragraph says
"Current hype around photonic is that photon qubits do not need to be cooled,... However, the components used to manipulate and detect photons, such as waveguides, beam splitters, and detectors, often rely on materials that require cryogenic temperatures."
A practical quantum computer is said to need more than millions of errorless qubits ( this-4th-paragraph ), which is impossible to realize forever.
Even the recent photon quantum computer (= still Not a computer ) has only 5 error-prone qubits (= each qubit can take only 0 or 1 ) that cannot calculate anything ( this-abstract used just 9 qubits ).
The last-Future expectation of this recent overhyped news says
"In the future, in order to make photonic quantum computers truly practical, we plan to solve issues (= still impractical, many issues remain to be solved )"
↑ The latest research of this Riken and NTT team used only (impractical) 7 photons (= 7 qubits = still Not a computer, this p.13 ) that could not calculate anything, contrary to their hypes such as "cloud computer".
(Fig.2) A photon or very weak light is too easily lost. which makes it impossible to scale up photon or optical quantum computer ↓
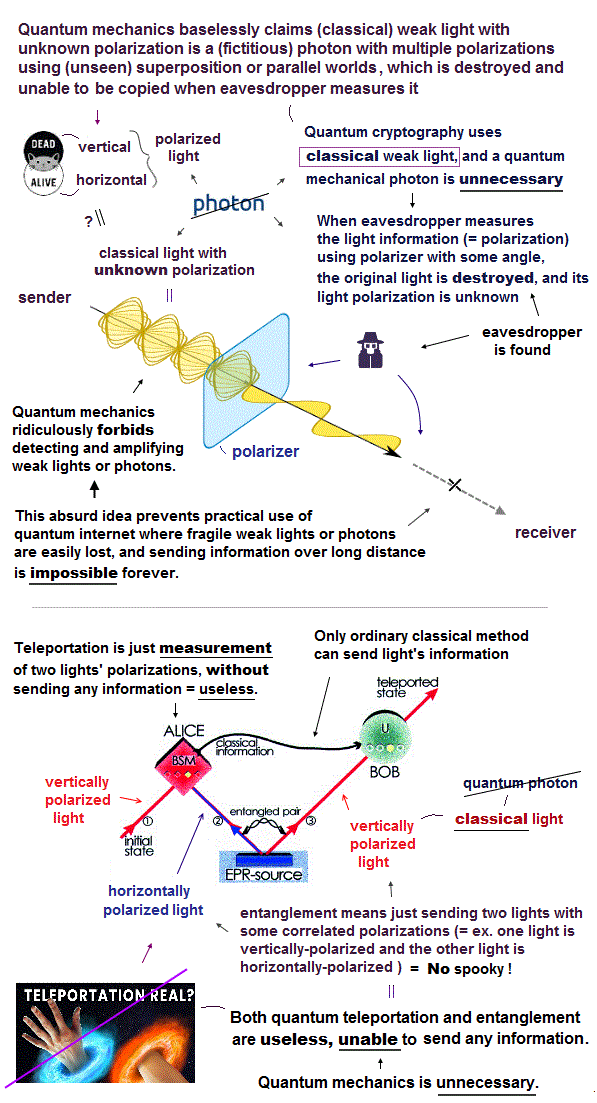
Photon quantum computer tries to use a fictional photon particle or weak light as a quantum bit or qubit.
Each photon or light's polarization is often used as a qubit state (= vertically-polarized light is used as a qubit's 0 state, horizontally-polarized light is used as a qubit's 1 state ).
In a photon quantum computer (= still Not a computer ), when each photon or weak light splits at a beam splitter (= BS ) into the upper path (= upper waveguide ) or the lower path, these paths or waveguides are used as a photon qubit's two states (= each qubit can take 0 or 1, a photon in the upper path means a qubit's 0 state, a photon in the lower path means a qubit's 1 state, this p.1-Fig.1, this-Figure 1, this 2nd-paragraph ).
When a photon (= just weak divisible classical light wave ) magically splits into both upper and lower paths at a beam splitter, it is treated as quantum superposition where each photon can be both in the upper and lower paths simultaneously using fictional parallel worlds ( this p.35-Fig.3.5 ).
↑ Of course, this quantum superposition or parallel worlds are just fiction.
A photon is just a divisible weak light that can realistically split at a beam splitter.
This 9th, 11th paragraphs say
"Then, photons are moving inside a waveguide in one direction (could be compared to plumbing pipes where you send water in). Each waveguide is called a mode, the unit of light in each mode is used to represent a qubit, two modes and one photon can encode 1 qubit. Imagine the modes as two parallel lines where the photon can be either on the upper line or the bottom line. At this point we can agree that having a photon on the upper waveguide corresponds to qubit in state |0> and the lower waveguide corresponds to qubit in state |1>, and this is the general idea that defines our qubits. We call it dual-rail encoding"
"For instance, assume we have |0> how do we end up in a quantum superposition ? ..
Once the single photon passes into a beam splitter it will move randomly in the upper or lower mode with a 50–50 chance. Furthermore, we might need different probabilities for example 30–70% or 40–60%, in that case we must have more sophisticated beam splitters using phase shifters (also called unbalanced beam splitters)."
(Fig.3) Photon qubits (= just weak classical light ) are too fragile, lost too easily to be a practical quantum computer ↓
The problem is a fragile photon or weak light so easily gets lost that quantum computers using such unstable photons as qubits are impractical forever ( this 4th-paragraph, this p.5-right-4.4, this p.1-left-2nd-paragraph ).
This-middle Photonic networks say
"Unlike with other qubit technologies, two-qubit gates in photonic networks are probabilistic (= random, causing errors ), not deterministic."
"..However, fidelity at scale is a significant hurdle for photonic networks. The largest source of error for photonic networks is photon loss during computations."
This Challenges of Photonic Quantum Processors say
"Losses: Photons are easily lost, limiting the performance of photonic quantum processors.
Control: It is difficult to control photons' behaviour, making it challenging to perform complex quantum operations.
Error correction: Quantum computers are susceptible to errors, which means that error correction techniques need to be developed to ensure the accuracy of calculations."
This 2nd-paragraph says "One of the main challenges in photonic quantum computing is the loss of photons"
This-p.1-right-2nd-paragraph says
"The remaining criteria are harder to satisfy because photons don’t easily interact, making deterministic two-qubit gates a challenge (= still useless, because changing a qubit based on another qubit state = two-qubit gate operation needed for computation is impossible ). Among the additional technical considerations is photon loss,.."
".. And although photons are always flying, computing and networking tasks may need them to be delayed or stored (= usually very long bulky light cables to confine the always-flying photons or light are needed ), so an extra device—an optical quantum memory (= still impractical ) —may sometimes be needed."
↑ The impractical photon quantum computer with easily-lost photons ( this p.1-right-1st-paragraph ) motivated physicists to focus only on detecting meaningless random photons (= just divisible weak classical lights ) in fake quantum advantage.
Due to the significant photon loss, the speed of detecting (easily-lost) photon qubits is much much slower (= only 10 Hz = only 10 photon qubits can be detected per second, impractically slow ) than other ( superconducting ) qubits (= 1.4 MHz = 1400000 Hz ), as shown in this Platform's table~.
(Fig.4) Photon quantum computer cannot manipulate qubits nor calculate anything by (impractical) logic gates. ↓
A real computer needs logic gates which change the state of a bit (or qubit ) 0 ↔ 1 by other bits (or qubits ) for calculation.
But a photon quantum computer still cannot realize even one two-qubit logic gate (= two-qubit gate operation means "change one qubit state 0 ↔ 1 based on another qubit state" ) consisting of (classical) beam splitters (= BS ).
This p.3-A universal set of quantum gates say
"arbitrary single-qubit operations can be expressed as combinations of beamsplitters and phase-shifters—an
optical interferometer (= for changing photon qubit state or path )...
The implementation of two-qubit gates is a challenge for photons. The fact that photons do not interact also means that it is difficult for the operation on one photon depend on the state of the other."
This p.1-introduction-1st-paragraph says
"in photonic systems, weak photon-photon interaction renders two-qubit gates
difficult (= photon quantum computers cannot calculate anything by conducting gate operation )"
This recent paper on (useless) photon's two-qubit logic gate (= one photon's state influences the other photon's state ) ↓
p.1-Abstract says "The experimentally achieved efficiency in an optical controlled NOT
(CNOT) gate reached approximately 11% in 2003 and has seen no increase since (= photon's two-qubit gate operation error rate is impractically-high = 89% = 100% - 11% efficiency )..
We demonstrate a CNOT gate
between two optical photons with an average efficiency of 41.7% (= still error rate is impractically high = about 60% )"
↑ Efficiency is the success rate or the probability that a desirable photon was detected by a photodetector ( this p.1-3rd-paragraph ).
This success rate (= efficiency) was still very low = only 41.7%, which is useless.
↑ So the error rate (= more than 60% error rate ) of a photon two-qubit gate operation is impractical and far worse than error rates (= 1%) of even other (impractical) superconducting or ion qubits
↑ The same paper ↓
p.2-Fig.1 shows photon's quantum computer's two-qubit logic gate consists of (classical) polarizing beam splitters and mirrors where two lights destructively or constructively interfering determine the final qubit state (= which path photon is detected in the last ).
p.4-left-C. says "The efficiency of the gate is the probability that no photon is lost inside the gate, if one control and one target photon impinge on the gate"
p.9-left-1st-paragraph says "Multiplying this by the 41.7% average efficiency of the gate, one obtains a 24% probability of detecting a two-photon coincidence per incoming photon pair (= only 24% photons could be detected, which means the remaining 76% photons were lost, or its error rate is extremely high = 76% )."
p.9-left-2nd-paragraph says "obtain a naive estimate for the two-photon coincidence rate of 10 s−1 (= only 10 pairs of photons or 10 qubits were detected per second, which is too slow and useless as a computer due to massive photon loss )"
(Fig.5) Photon qubits are too easily lost. ← Detecting multiple photons (= qubits ) simultaneously is unrealistic. ↓
To scale up photon quantum computer, physicists need to simultaneously detect as many photons (= each photon is used as a qubit taking 0 or 1 states ) as possible.
If they cannot simultaneously detect multiple photons or multiple qubits, it means photons or qubits relevant to calculations are lost (= so calculation using the easily-lost photons is impossible ), or irrelevant background photons are mixed.
So increasing success rate of simultaneous detection of multiple photons or qubits is indispensable for scaling up the photon quantum computer.
But the present simultaneous photon detection rate is too bad and too low to scale up a photon quantum computer (= even success rate of detecting only small numbers of 4 ~ 8 photons or qubits is unrealistically low and too bad ).
p.4-right-Experimental design says "pumped by a femtosecond ultraviolet laser (390 nm, 76 MHz = 76 × 106 photons or weak light pulses were generated )"
p.5-left-last paragraph says "the final fourfold coincidence rate (= rate of detecting only 4 photons simultaneously ) is about 0.03 Hz (= 1 Hz or Hertz means detecting one photon per second )."
↑ It means only 0.03 photons (= 0.03 simultaneous four-photon detection ) per second were detected (= only 0.03 × 4 = 0.12 photon bits or information per second can be utilized ), which is too few and too slow to use as a computer's memory (qu)bits.
Simultaneous four-photon detection rate was 0.03/76000000 = 0.000000001 = 99.9999999 % error rate due to photons' loss , which is completely impractical.
This another recent research paper ↓
p.2-left-2nd~3rd-paragraph says "pulse laser with a repetition rate of ∼76 MHz, the QD emits ∼50 MHz polarized resonance fluorescence single photons at the end of the single-mode fiber (= about 50 MHz or 50 × 106 photons or light pulses were generated from the light or photon source )"
p.5-Fig.4a shows the six-photon coincidence counts (= the total number of detecting 6 photons simultaneously ) were only less than 300 per 23 hours, which counts were too few and too slow to be practical.
↑ Only 300 × 6 = 1800 bits (= each bit can take only 0 or 1 ) or 1800 photons could be used per 23 hours, which pace is too slow to use as practical computer's memory bits due to massive photon loss.
↑ the 6-photon simultaneous detection rate was only 300/(50 × 106 × 3600 × 23 ) = 0.0000000001, which is extremely low, and useless.
p.1-right-last-paragraph says "That is, by combining a quantum dot (QD)–based photon source, from which we measure single-photon count rates at 17.1 MHz (= 17.1 × 106 photons were estimated to be generated from light source per second )"
p.5-Fig.4c shows the coincidence 8 photon count rate drastically decreased to only less than 0.01 Hz (= less than one detection per 100 seconds ) from the original single photon rate of 17.1 MHz (= 17100000 Hz ), which means success probability of detecting 8 prepared photons simultaneously is only 0.01/17100000 = 0.000000001.
↑ Detecting only 8 photons or 8 qubits is too slow (= just 0.01 detections per second ), hence, building just 9 ~ 10 photon qubits is impossible, which is far from a practical quantum computer that will require millions of qubits.
As a result, the probability of detecting multiple photons simultaneously is extremely low and disastrous, which large photon loss makes it impossible to scale up photon's quantum computer forever.
(Fig.6) Only a few (fragile) photon qubits can be generated per second ? ← this is too slow and too impractical.
This introduction and lower-Challenge: Generation of error-correctable state — GKP state say
"However, a significant challenge lies in generating specialized states like the Gottesman-Kitaev-Preskill (GKP) state (= a photon's logical qubit mixing multiple weak lights or photons, this p.1-abstract ), crucial for error correction and achieving fault tolerance"
"indicating the successful projection of the last mode into a GKP state. Nevertheless, this approach is probabilistic, with a success rate as low as 1% or even lower (= photon error correction needs to create GKP light superposition state, which success rate is only less than 1%, which is useless )"
The recent research tried to generate this fault-tolerant photon's GKP state (= a photon's logical qubit, this p.1-abstract ), but still No photon's error correction has been realized even in this latest research.
↑ This research paper ↓
p.2-right-2nd-paragraph says "Our generation method is based on the two-mode interference between cat states (= just states mixing multiple weak classical light waves )"
p.4-right-last~p.5-left says
"there are still future
technological improvements to be made (= still useless ). Our current limiting factor is the optical loss in the system."
p.5-left-1st-paragraph says ". Our current setup has the success rate of about 10 Hz which is not sufficient for actual computation (= only 10 photon GKP-states or 10 qubits per second were generated, which is too few, too slow, useless, and this research did Not conduct error correction )"
This p.5-2nd-paragraph says
"The generation rate of each cat state in the GKP state generation is about 200 kHz. The
duty cycle for the sample & hold is 40% and taken into account of the allowed time window for
simultaneous detection of ±0.6 ns, the simultaneous detection of the two cat state is expected
to be (2 × 105 = 200 kHz )2
× (1.2 × 10−9 = detection efficiency
) × 0.4 = 19 Hz, which is on the same order with actual
simultaneous detection rate of 10 Hz (= only 10 photon qubit states per second were generated, which was too slow, too few to use as a practical computer )"
↑ Two photon simultaneous detection rate was extremely low = only 1.2 × 10−9 due to extremely large photon loss.
As a result, the significant photon loss hampers the realization of a photon quantum computer (forever).
Feel free to link to this site.
