平坦なクラインの壺
すべての場所でゼロの曲率になっているクラインの壺のことを『平坦なクラインの壺』と呼ぶことにすると、４次元（以上の）空間の中では、平坦トーラスと同様に『平坦なクラインの壺』を実現することができます。
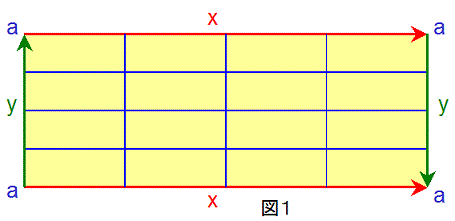まず、クラインの壺を作ってみましょう。図１に示した長方形において、
４つの点“a”が、同一の点になるように、
２つの線“x”が、矢印の向きで同一の線になるように、
２つの線“y”が、矢印の向きで同一の線になるように、
折り曲げると、クラインの壺ができあがります。しかし、３次元空間の中で、このような折り曲げを行おうとしても、面どうしが
交差してしまうため、実現できません。
すなわち、クラインの壺は、３次元空間の中では実現できないことがわかるかと思います。したがって、平坦なクラインの壺も
３次元空間の中では実現できません。
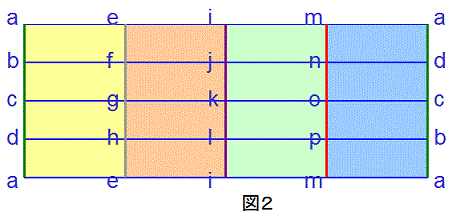では、４次元空間の中で、平坦なクラインの壺を作ってみましょう。
図２は、前述の長方形（図１）と基本的には同じものですが、以下の説明のために、記号や色分けを変えたものです。
まず、この長方形を、色分けされた領域で縦に４分割し、各領域の上辺と下辺を接合すると、４つの角柱状の筒型ができます。
次に、これらの４つの角柱状の筒型を、４次元空間の中でつなぎ合わせてみましょう。なお、４次元空間（より正確に言うと、
４次元ユークリッド空間）を表す４つの座標軸を、x軸、y軸、z軸、w軸とします。
図３−１は、図２の左端の領域から作った筒型を、w=w0 での x-y-z座標系に配置していることを示しています。
なお、筒型の両端のy座標は、y=y0、y=y1 となっているとします。
図３−２は、図２の左から２番目の領域から作った筒型を、y=y1 での x-z-w座標系に配置していることを示しています。
なお、筒型の両端のy座標は、w=w0、w=w1 となっているとします。
図３−３は、図２の左から３番目の領域から作った筒型を、w=w1 での x-y-z座標系に配置していることを示しています。
なお、筒型の両端のy座標は、y=y0、y=y1 となっているとします。
図３−４は、図２の左から４番目の領域から作った筒型を、y=y0 での x-z-w座標系に配置していることを示しています。
なお、筒型の両端のy座標は、w=w0、w=w1 となっているとします。
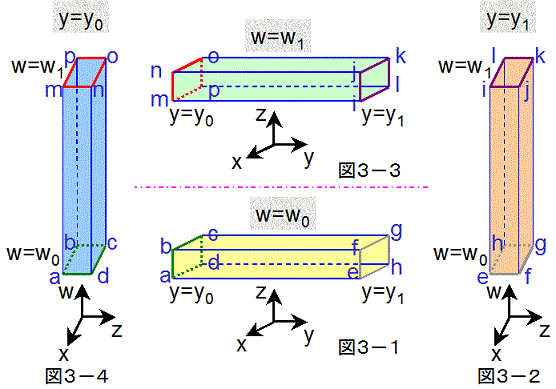
図３−１〜図３−４を見比べると、４つの筒型の端は、順番につなぎ合わされていることがわかると思います。まず、図３−１の
筒型の右端（点e、f、g、hを結ぶ、灰色の閉曲線）では y=y1, w=w0 ですが、図３−２の筒型の下端でも
y=y1, w=w0 なので、２つの端どうしの位置が一致しています。すなわち、この２つの端はつなぎ合わされて
いることがわかります。そこで、図３−２の筒型の下端も、e、f、g、hを結ぶ、灰色の閉曲線として表しています。同様に、図３−２の
筒型の上端と図３−３の筒型の右端（i-j-k-l：紫色）も、ともに y=y1, w=w1 なので、この２つはつなぎ合わ
されています。さらに、図３−３の筒型の左端と図３−４の筒型の上端（m-n-o-p：赤色）も、ともに y=y0, w=w1
なので、つなぎ合わされています。最後に、図３−４の筒型の下端と図３−１の筒型の左端（a-b-c-d：緑色）も、ともに y=y0,
w=w0 なので、つなぎ合わされています。
結局、図３の４つの筒型の端どうしは順番につなぎ合わせれているので、クラインの壺を形成していることがわかります。しかも、
面の伸縮なしで実現されているので、平坦なクラインの壺となっています。
なお、図３−１〜図３−４の４つの筒型がどのように接続されているかと言うと、図３−１の筒型の外側の面が図３−２の筒型の内側の面
とつながり、図３−２の筒型の内側の面が図３−３の筒型の内側の面とつながり、図３−３の筒型の内側の面が図３−４の筒型の外側の面と
つながり、図３−４の筒型の外側の面が図３−１の筒型の内側の面とつながっています。
すなわち、このようにして構成されたクラインの壺は、トーラスと異なり、表と裏の区別のない閉曲面となっていることがわかります。
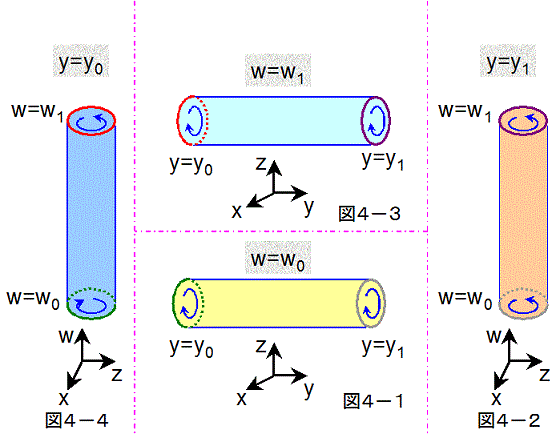今度は、円柱状の筒型を用いて、上述と同様の方法で、平坦なクラインの壺を作ってみましょう。
図４では、図３のそれぞれの筒型を、角柱状から円柱状に変えただけです。４つの筒型のつなぎ合わせ方は、今回も同様です。
同じ色の端どうしを、図中の青い矢印の向きに合わせてつなげば、平坦なクラインの壺ができあがります。
また、図３と場合と同様、図４−１の筒型の外側の面が図４−２の筒型の内側の面とつながり、図４−２の筒型の内側の面が図４−３の
筒型の内側の面とつながり、図４−３の筒型の内側の面が図４−４の筒型の外側の面とつながり、図４−４の筒型の外側の面が図４−１の
筒型の内側の面とつながっているので、このようにして構成されたクラインの壺も、表と裏の区別のない閉曲面となっています。
