電磁波と重力波

　はじめに、波（波動）には縦波と横波があり、縦波では波の伝搬方向と同じ方向に波が振動しますが、横波では波の伝搬方向と垂直の方向に波が振動します。例えば、x軸方向に伝搬する波（波動）は、一般に次式のように表すことができます（次式において、x：x軸座標、a：変位、t：時刻、A：最大変位（＝振幅）、T：周期、λ：波長、δ：初期位相です）が、次式における変位 a の向き（＝振動の向き）は、縦波では x軸方向と同じになり、横波では x軸方向と垂直になることがわかります。

　　　a＝A sin｛2π(t/T－x/λ)＋δ｝

　つぎに、横波には電磁波、重力波、地震のS波、水面の波などがありますが、このうち、電磁波と重力波は、いずれも光速で伝搬する横波で、それらの特徴をまとめると下表のようになります（下表において、ｃは光速（ｃ≒3.0x10⁸ m/s ）です）。

	波のタイプ	伝搬の速さ	振動の向き	振動するもの
電磁波	横波	ｃ	伝搬方向と垂直な方向	電界と磁界
重力波	横波	ｃ	伝搬方向と垂直な方向	２次元空間

　上表より、電磁波と重力波の違いは『振動するもの（＝変位するもの）』であるとわかります。すなわち、電磁波では電界と磁界が振動するのに対し、重力波では２次元空間が振動するのです。しかし、この違いはすぐにはわかり難いと思います。そこで、宇宙が３次元空間ではなく２次元空間と仮定して、電磁波と重力波の違いを以下に説明したいと思います。

　いま、右図のように、宇宙が２次元の球面であると仮定しましょう。

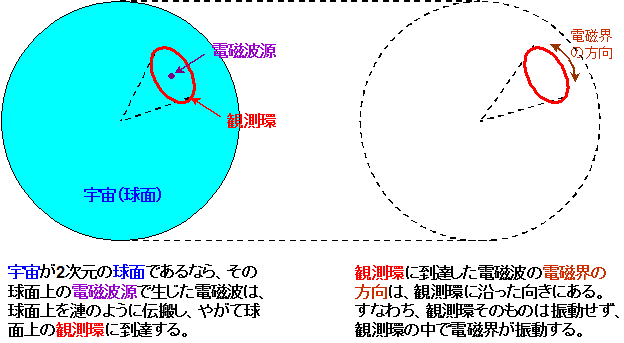
　はじめに、電磁波について考えます。まず、２次元球面（＝宇宙）のある場所（＝電磁波源）で生じた電磁波は、球面上を漣（さざなみ）のように伝搬し、やがて球面上の観測環に到達します。ここで、観測環とは、電磁波源から等距離にある円周（＝１次元球面）を指すことにします。すなわち、電磁波源で生じた電磁波は、観測環において同じ様に振動することがわかります。

　ところで、３次元空間の電磁波において観測環に相当するものは、電磁波源から等距離にある球面（＝２次元球面）となり、その球面に沿って電界と磁界が互いに直交する方向で振動します。しかし、右図における観測環は１次元であるため、電界と磁界をまとめて電磁界とすることにします。すると、その電磁界の向きは、伝搬方向と直交する向き、すなわち、観測環に沿った向きであることがわかります。よって、観測環に到達した電磁波の電磁界の方向は、観測環に沿った向きとなります。

　また、言うまでもなく、観測環そのものは振動せず、観測環の中で電磁界が振動することもわかります。

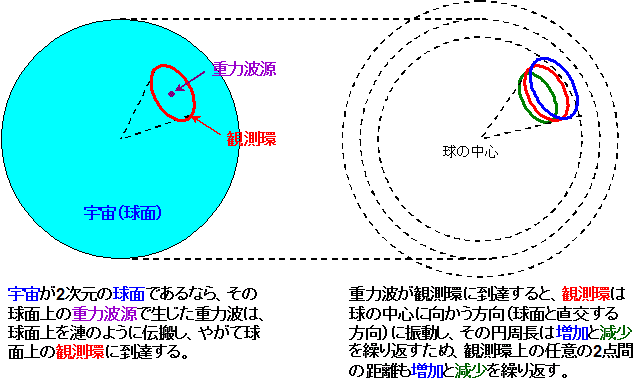　つぎに、重力波について考えます。上述の電磁波の場合と同様に、宇宙が２次元の球面であるなら、右図のように、その球面上の重力波源で生じた重力波は、球面上を漣のように伝搬し、やがて球面上の観測環に到達します。

　そして、重力波が観測環に到達すると、観測環は球の中心に向かう方向（球面と直交する方向）に振動しますが、このとき、右図からわかるように、観測環の円周長は増加と減少を繰り返します。すなわち、観測環そのものが伸び縮みするため、観測環上の任意の２点間の距離も増加と減少を繰り返すことがわかります。

　では、上記と同様に３次元空間の宇宙での重力波をつぎに考えることにします。例えば、我々の宇宙の形が３次元球面であると仮定しましょう。すると、上記の観測環に相当するものは観測球面（＝２次元球面）となり、重力波が観測球面に到達すると、観測球面そのものが第４の方向（＝宇宙（３次元球面）を表面とする４次元球体の中心に向かう方向）に振動し、それに伴い観測球面の表面積が増えたり減ったりするので、観測球面上の任意の２点間の距離が伸び縮みする、と考えられます。ここで、第４の方向とは、重力波の伝搬方向（＝第１の方向）とも観測球面に沿った互いに直交する方向（＝第２、第３の方向）とも直交する方向になります。すなわち、第４の方向は宇宙（３次元球面）と直交する方向であり、互いに直交する第１～第４の方向は４次元ユークリッド空間の各座標軸を成していることがわかります。

　なお、上記においては、宇宙を３次元球面と仮定しましたが、宇宙の形が３次元球面でない場合についても、同様の考え方で重力波を表すことができるでしょう。

　以上のことから、重力波検出装置の基本動作原理も理解できます。すわわち、地球表面の一部（≒観測球面の一部）にある３点Ａ、Ｂ、Ｃにおいて、線分ＡＢとＢＣの長さが等しく、ＡＢとＢＣの向きが直交している場合、重力波が到来したときにＡＢとＢＣの長さに差異が生じるので、その差異を観測すれば重力波を検出できるのです。具体的には、Ａ、Ｂ、Ｃの各位置にミラーやハーフミラーを設置し、ＡＢ、ＢＣの各経路でレーザー光を往復させ、各経路の長さの差異が生じたときに起こる光の干渉の有無を観測することで、重力波を検出することになります（注１）。

　2015年9月14日、上記の原理に基づく米国の重力波検出装置 LIGO により、世界で初めて重力波が観測されました（注２）。観測された重力波は、周波数が 35Hz～250Hz、振動期間が約0.15秒で、約13億光年の彼方にある連星ブラックホールの合体に伴って生じた重力波だったようです。さらに、このブラックホールの質量は、合体前の２つ（連星）はそれぞれ太陽質量の36倍と29倍で、合体後は太陽質量の62倍となり、合体の際に太陽質量の3倍の質量が重力波に変化した、と推測されています。

　ところで、ブラックホールの質量は、ブラックホールを取り囲む事象の地平線の内側の特異点に存在している、と考えられます。このことと上記の観測結果を考え合わせると、２つのブラックホールが合体して一部の質量が失われるとき、その質量に相当するエネルギーが重力波に変化し、その重力波は事象の地平線を透過して宇宙空間に放出されることがわかります。すなわち、電磁波や各種素粒子とは異なり、重力波にとって事象の地平線は存在しないのです。少し不思議な感じもしますが、ブラックホールからの重力が事象の地平線の外側に伝わることを考えれば、納得できるでしょう。なぜなら、電磁気力が伝わることと電磁波が伝搬することが同じであるのと同様に、重力が伝わることと重力波が伝搬することは同じであるからです。

（注１）参考資料　：　Wikipedia　『マイケルソン干渉計』
（注２）参考資料　：　Wikipedia　『重力波（相対論）』、『観測された重力波の一覧』