フーリエ級数展開

井澤　裕司　　

フーリエ級数展開 は、 信号 と スペクトル の関係を理解する上で最も重要な概念です。

その内容が把握できれば、 フーリエ変換 や 離散フーリエ変換 、 サンプリング の物理的な意味や、

それらの相互関係を理解することも容易です。

ここでは、数学的手法に基く厳密な解説は避け、より 直観的 に理解できるような ツール をいくつか用意しました。

図中の ボタン を 操作 することにより、 関数の 波形 や フーリエ係数 等の数値を インタラクティブ に 変更 することが可能です。

これらを活用して、 信号の対称性 と フーリエ係数 の関係や、 直交関数 のイメージについて、理解を深めて下さい。

1.　定義(その１)

はじめに、 フーリエ級数展開の定義 を示しましょう。

周期関数を x(t) とします。ここで ｔ は 時間 、 T₀  は 周期 を表します。

この関数が、 ディリクレの条件 を満たすとき、 T₀  の整数倍の周期をもつ sin と cos の 重ね合せ により表すことが

できます。

すなわち、以下の式が成立します。

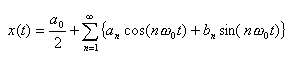
ここで、 ω₀ は基本となる 角速度 であり、基本となる 周期 T₀ に対応する基本周波数を f ₀ とすると、

ω₀  = 2πf₀ = 2π／T₀ の関係が成立します。

この a_n , b_n という係数は、それぞれ x(t) に含まれる cos 成分 と sin 成分 の大きさを表しており、

x(t) が定まれば これらの値は一義的に確定します。

逆に、係数 a_n , b_n を用いて、 x(t) を表現することができます。

詳しくは後ほど説明しますが、この a_n , b_n を拡張すると、 x(t) の周波数成分、すなわち スペクトル になります。

なお、係数 a₀  の 1/2 は、直流と正弦波の平均電力を一致させるための 補正係数 です。

その意味は後で説明しますので、ここでは気にしないで下さい。

［確かめてみよう］ 　−重ね合せの原理−

実際に、「様々な周期関数が、cos と sin の重ね合せで表すことができるのか？」 疑問に

感じる人もいるでしょう。

以下、 方形波 や 三角波 、 全波整流 等、代表的な関数について確認してみましょう。

　

左の 関数 の ボタン を１つ選び、 マウスでクリック して下さい。

指定した関数が、低い次数から段階的に生成されてゆく過程が アニメーション で表示されます。

上の波形は次数が n の cos の 基本波 （振幅=１）、中央の波形は sin の 基本波 です。

次のステップで、それらに係数  a _n , b _n をかけた波形が表示されます。

最後にこれらを加算した波形が、下側に表示されます。

cos は周期関数の 偶対称成分 、 sin は 奇対称成分 に対応することは、容易に理解できると思います。

このように、適切な係数 a _n , b _n を選び、これに対応する正弦波を低い次数から段階的に加えてゆくと、

目的の関数に収束することがわかります。

［問］

関数の形状により、 収束 する 速度 が大きく異なります。

どのような関数で収束が遅くなるか、検討して下さい。 （ 答 ）

［確かめてみよう］ 　 -周期関数の波形と係数の関係-

ここで、実際にフーリエ係数 a_n , b_n を操作して、それらを重ね合わせた関数 x(t) がどのように変化するか、

観察してみましょう。

図には3つの波形が表示されています。

上の波形は、次数が 9次 までの cos と sin の総和 x(t) を表しています。

中央は cos のみ、下は sin のみの 総和 に対応しています。

言うまでもなく、中央と下の波形を合わせると上の波形に一致します。

一方、下の棒グラフは、フーリエ係数 a_n , b_n の値を表しています。

左が cos 成分 の a₀  〜 a₉ 、右半分は sin 成分 の b₀  〜 b₉ を表しています。

＋ や − の四角の部分をクリックすると、それらの値が調整できるようになっています。

例えば、係数 a₀  の ＋ をクリックして下さい。 cos の 0次成分 、すなわち 直流値（平均値） が少しずつ

増えてゆきます。逆に − をクリックすると、 減少 します。

また、左の関数のボタンを繰り返しクリックすると、 周期関数 の 位相 がずれてゆきます。

位相の変化により、係数 a_n , b_n がどのように 変化するか、観察して下さい。

［問］

関数 x(t) が中央で折り返した形となる 偶対称 のとき、係数 a _n , b _n の値がどのようになるか、検討して下さい。

また、中央で上下、左右が点対称となる 奇対称 の場合についても、調べて下さい。（ 答 ）

2.　定義(その２) 　 −係数 a_n , b_n の求め方−

周期関数 　　　ｘ(t) が定まったとき、係数 a_n , b_n をどのように求めるかが問題となります。 結果を以下に示します。

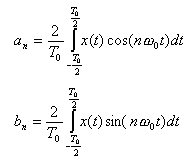
a_n を求める場合は、 x(t) に cos(nω₀t) を乗じ、時間 t で １周期 の範囲を 積分 します。

b_n の場合は sin(nω₀t) となります。

「なぜ、このような方法でこれらの係数の値が求まるのか？」 　

その理由を理解するためには、 三角関数（ cos, sin ） の 直交性 について説明する必要があります。 　

3.　三角関数の直交性について

三角関数の sin、 cos は 直交関数系 を構成します。

たとえば、整数 m、 n について以下の関係式が成立します。

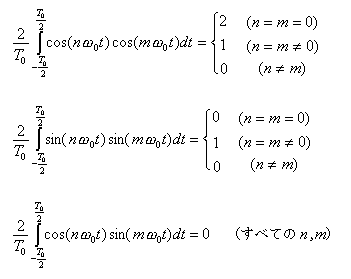
この積分の形は、内積 と呼ばれます。

［確かめてみよう］ 　- 三角関数の直交性について -

この 三角関数 の 直交性 について、次の図を用いて補足しましょう。

図の左上は、次数 n の cos , sin の波形を示しています。

また左下は、次数 m の波形です。これら２つの関数の積は4通りあり、それらの波形を右側に示しています。

中央に次数の n , m の値が表示されています。

ボタンの ＋ と − をクリックすることにより、 任意 の値にセットすることができます。

デフォルト 値は、それぞれ n = 2 と m = 3 です。

右の波形の 平均値 （0 〜 T₀　における積分値）を 緑色の線 で示しています。

ほとんどの場合、この値は 0 になっています。

n , m の値を変化させて、平均値が 0 以外 の値になる 組み合せを求め、その条件を検討してみて下さい。

直交性に関する結果は、以下のようになります。

(1) cos×cos の平均値

• n = m = 0 のとき　1
• n = m ≠ 0 のとき 1/2
• n ≠ m のとき、すべて 0

(2) sin×sin の平均値

• n = m = 0 のとき　0
• n = m ≠ 0 のとき 1/2
• n ≠ m のとき、すべて 0

(3) cos×sin 、 sin×cos の平均値

• すべての整数 n, m について、 0

(1) において、 n = m = 0 の積分値が n = m ≠ 0 の 2倍 になっています。

フーリエ級数展開 の定義において、係数 a₀  の場合にのみ、 1/2 という 補正係数 が付くことを説明しましたが、

これがその根拠になっています。

(2) より b₀ = 0 となり、 b₀ の項は存在しません。

これが 直交性 という条件です。この特性は極めて有用で、信号をある基本的な関数の重ね合せに

分解したり、逆に合成して元の信号を復元したりすることができます。

三角関数はその代表的なものですが、 直交関数 については、 ウェーブレット関数 をはじめとして、

各方面で研究が進められています。

この関係を三角関数の数式で表すと、次のようになります。

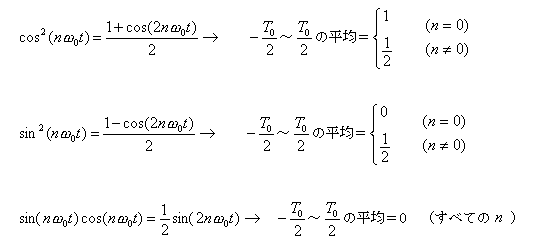
4.　重ね合せの原理

三角関数 の 直交性 については、理解できたと思います。この性質を用いると、周期関数 ｘ(t) から

フーリエ級数の係数 a_n , b_n を求めることができます。

その前に 重ね合せの原理 について整理しておきましょう。

周期関数 を x₁(t) , x₂(t) とし、それらを フーリエ級数展開 した係数をそれぞれ、 a_1n , b_1n と a_2n , b_2n とします。

このとき以下の関係式が成立します。

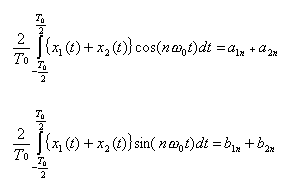
すなわち、周期信号を 複数 の信号の 和 に 分解 したとき、その周期信号の フーリエ係数 は、分解した信号の

フーリエ係数の和になります。

［補足］　−係数 a_n , b_n の求め方−

ここでは、係数   a_n , b_n の求め方について補足します。この求め方については、 直交性 より明らかですので、

既に理解している人は次のステップに進んで下さい。

次の式は最初に示した フーリエ級数展開 の定義です。（ただし、整数の変数 n を m に変更しています。 ）

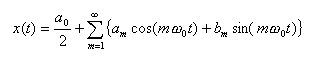
この x(t) の右辺を、次の  a_n , b_n に代入します。

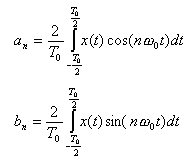
上で述べた 重ね合せの原理 を用いて分解し、 直交性の条件 を用いて整理します。

その結果、三角関数の 直交性 より m = n 以外の項はすべて 0 となり、最終的に a_n = ‥ = a_n, b_n = ‥ = b_n と

いう関係が導かれ、 係数 a_n, b_n の値が得られることがわかります。

以上の計算が正しいことを、 シミュレーション により確かめてみましょう。

次の図に、３つの波形が表示されています。上の波形がもとの周期関数 x(t) です。

この関数をフーリエ級数展開し、その係数 a_n , b_n を求めます。

はじめに、求める係数を cos 成分の a₀ 〜 a₉ 、 sin 成分の b₀ 〜 b₉ の中から選択します。

＋ や − の四角の部分をクリックして下さい。

例えば、 a₄ を選択すると、その部分が濃いグレーで表示され、対応する基本波（振幅１）が中央に表示されます。

また、下には、周期関数 x(t) と 基本波の積 が表示されます。その積を1周期で積分した値

（すなわち1周期の平均値）を 緑色の線 で表しています。

この値を、 2/T₀ 倍した値が、求める係数 a₄ に相当します。

左のボタンで関数を切り替えたり、他の係数をクリックして、 フーリエ係数 が求まることを感覚的につかんで下さい。

5.　複素フーリエ級数展開

フーリエ級数展開 では、周期関数を三角関数の 成分 に 分解 し、最終的にいくつかの係数 a_n , b_n に変換します。

係数の a_n は周期関数の 偶対称成分 (cos) に、 b_n は 奇対称成分 (sin) に対応しています。

これらの関数や係数はすべて実数です。

本節では、これらを 複素数 を用いてエレガントに拡張した 「複素フーリエ級数展開」 について説明します。

この概念は、次章以降で述べる 「フーリエ変換」 や 「離散フーリエ変換」 に密接に関連していますので、

十分理解するようにして下さい。

たとえば x = cos(θ) 、 y = sin(θ) とおくと、 xy 平面上での 単位円周上 の1点に対応します。

すなわち、2次元の直交座標における回転を1次元の２つの座標軸で観測したものが、三角関数に対応します。

逆に、三角関数の cos と sin をペアにして拡張すると、 2次元 上の 回転 に対応させることができます。

すなわち、実数と虚数の 複素平面 上の1点に対応させる方法です。

具体的には、フーリエ係数の a_n を実部、係数 の b_n を虚部に対応させ、 Z_n = a_n + jb_n とおくと、

これが 回転成分 に対応します（ j は 虚数単位 ）。

この 複素数 を スペクトル と名付けます。

それでは、通常の 「フーリエ級数展開」 から 「複素フーリエ級数展開」 を導く準備として、

複素数の基本となる オイラーの公式 について説明しましょう。

[補足]　Euler（オイラー）の公式について

複素平面 における 半径１ の 単位円 を考えます。

この円上の点を、角度 θ を用いて、以下のように表すことができます。ここで、 j は 虚数単位です。

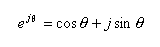
これを 「オイラーの公式」 と言います。

この e は自然対数の底で、微分してはじめてその意味がわかる不思議な数です。

オイラー自身、「真の数学者は、 θ に π （円周率：パイ） を代入した e^ｊπ＝-1 　という式の意味がわかる。」という言葉を残しています。

e と π はともに 無理数 で、この式は不思議といえば不思議です。

元気のある人は、挑戦して下さい。（ヒント。 e^ｊθ を θ で微分し、 j の解釈に一工夫必要です。）

この式を変形すると、次のようになります。

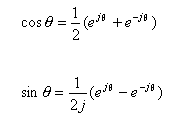
ここで、 a_n と b_n を用いて、次の複素数 c_n を定義します。ここで、整数 n は 負 の値を取り得ることに注意して下さい。

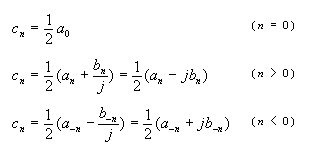
これらの式を用いて、 フーリエ級数展開 の式を変形すると、次の式が得られます。

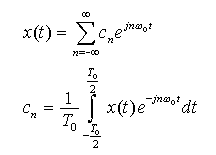
上が複素フーリエ係数 c_n を用いて 周期関数 x(t) を表す式、下が周期関数 x(t) から 複素フーリエ係数 c_n を

求める式になります。

この c_n のことを スペクトル と言います。

x(t) が 実数 のとき、任意の整数 n について c_n の虚部の符号を反転したものが c_-n に等しくなります。

すなわち、これらは 複素共役 の関係にあります。

[補足]　−複素数とは何か？　（回転と振動について）−

ここで、 複素数を導入する意義・目的 について考えてみましょう。

皆さんの中には、 複素数 、あるいは 純虚数 j をつかみところのない存在だと感じている方がいるのではないでしょうか。

しかし、 複素数 は 振動現象 を 単純明快 に表すという明確な目的があって導入された数学的な道具 であり、物理的な
意味付けも可能です。

ここで、身の回りにある機械、例えばあなたが使用しているコンピュータを例に挙げて考えてみましょう。

コンピュータの中には、様々な メカニズム（運動機構） が使われています。

電子回路の動作は直接目にすることはできませんが、 CPUの冷却用ファンをはじめとするモータが目に入ります。

ハードディスク等の記録用ドライブからもモータの回転する音が聞こえてきます。

CDドライブやDVDドライブのトレイは往復運動をしますが、これも内部のモータの 回転 を歯車を用いて 往復運動 に変えています。

すなわち、機械類には、 往復運動 ではなく 回転運動 が圧倒的に多く使用されていることがわかります。

その理由は何でしょうか？　それは 単純だから です。

往復運動 は一種の 振動 であり、数学的には 正弦波 などの関数を用いて表すことが可能です。

一方の回転運動 を数学的に表そうとすると、 奥行き方向 の次元（すなわち 虚数軸 ）が１つ増えてしまいます。

しかし、このように次元が増えたとしても、 回転 は振動よりはるかに 単純 な運動であり、数学的にも 回転（複素数） の方が、

振動（正弦波などの実関数） より 単純・明快に表現 できるのです。（後半の章で実感できると思います。）

具体的な例を示しましょう。

下のアニメーションで、 赤 と 青 の線は、進行方向に向かって 時計方向 と 半時計方向 の 回転運動 を表しています。

2つの回転速度は等しく、位相も揃えてあります。

これらの回転を 横方向 から眺めると（すなわち虚数部を無視すると）、単純な１つの 正弦波 の 振動 に見えます。

ここで、 「虚数部を無視すると‥」 　という文章は極めてあいまいな表現です。

また、 「振動運動を回転とみなす」 　という部分が気になる方もいるでしょう。

このとき、物理的には次のように解釈すればいいでしょう。

上のアニメーションにおいて、 ２つの回転運動 （ 赤 と 青 ）の 重ね合せ（ベクトル和） をとると、 虚数部 = 0 となり、実数の平面内の

振動運動 に等しくなります。 空色 （シアン） の正弦波がこれに相当します。

（ちなみに2つの回転運動の積は１、すなわち静止状態となるので、注意して下さい。）

この2つの 回転運動 の 振幅 と 位相 は等しく、回転の 方向 だけが 反転 しており、いわゆる 共役（複素数） の関係にあります。

すなわち、 振動現象 を回転方向だけが異なる２つの 回転運動 の ベクトル和（重ね合せ） と考えて、それらの成分（ 複素数 ）の

各々について、必要な計算処理を行い、最後にその ベクトル和 をとれば、振動現象に戻るわけです。

正弦波 の周波数は周期の逆数となるので、 負の周波数 は定義できませんでした。

しかし、回転の場合、 2つ の 回転方向 のそれぞれに 正と負の周波数 を割り当て、区別する必要があります。

なお、これらの手法を用いるためには、 「重ね合せの原理」 が成立することが条件となります。

[参考]　−コイルばねの重ね合せ−

この章の前半で、ディリクレの条件を満たす 周期信号 は、 その整数倍の角周波数をもつ

cos と sin の 和 、すなわち 重ね合せ により、表現できることを学びました。

また、先ほど cos や sin などの 正弦波 は、 時計方向 と 反時計方向 に 回転 する

2種類の 螺旋（らせん） すなわち コイルばね の 重ね合せ により、表わされることを示しました。

これらを組み合わせると、ディリクレ条件を満たす 周期波形 は、いくつかの 角周波数 (nω) をもつ

コイルばね の 対 ( c_n , c_-n ) の 和 、すなわち 重ね合せ により、表現できることが分かります。

　

これが、先に示した 複素フーリエ級数展開 の最初の式の意味です。

これらの関係を、 次の図 に示します。

ここで、整数 n > 0 のとき c_n は 時計方向に n 回転、 c_-n は 反時計方向に n 回転する成分を表しています。

これらは フーリエ変換 の基礎になりますので、 その イメージ をしっかり把握して下さい。

[参考]　−時計の秒針を静止させて観察するには？−

時計の 秒針 を 静止 させて観察するには、どのような方法があるでしょうか？

下の図を見て考えてみましょう。

答えは簡単です。

秒針 と 同じ速度 で 逆方向（反時計方向） に 回転する台 に乗せて観測すればよいのです。