今回もリストのお話です。しかし、前回とはちょっとだけ違います。
それでは、今回の要点です。
では、いってみましょう。
 |
| 図.1 挿入法 |
|---|
リストは、ポインタを介してデータを数珠繋ぎにしたものでした。今回はこのリストのソートをやってみたいと思います。
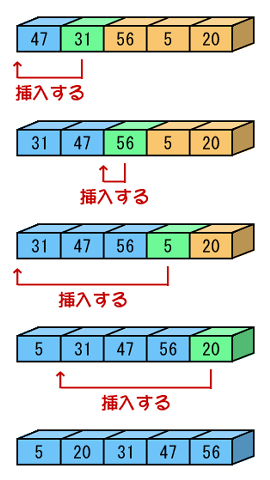
前回言ったように、リストのソートには挿入法(第26章参照)が使えます。しかし、前回のリストを挿入法でソートしようと思っても、実はかなり面倒なことになります。それは、後ろからも要素をたどっていくことができないからです。
図.1の通りの順番で考えると、挿入箇所を探すのに逆にリストをたどっていく必要があります。左右対称にして考えるとしても、挿入する要素の位置を毎回探す必要があります。
しかし、後ろから要素をたどっていく必要があるのなら、後ろからも要素をたどれるようにすればいいのです。実現は簡単です。次の要素へのポインタだけでなく、前の要素へのポインタも持っておけばいいのです。
図にするとこんな感じです。
 |
| 図.2 後ろからもたどれるリスト |
|---|
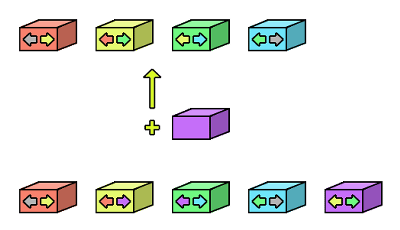
リストの各要素は2つのポインタを持っています。1つはこの要素の前の要素への、もう1つは次の要素へのポインタです。
先ず、赤色の要素があります。前の要素はないので、1つ目のポインタには要素がないことを表す値を入れておきます。そして、次の要素は黄色の要素なので、2つ目のポインタには黄色の要素のアドレスを入れておきます。次は黄色の要素です。前の要素は赤色の要素なので、1つ目のポインタには赤色の要素のアドレスを、同じようにして2つ目のポインタには緑色の要素のアドレスを入れます。このように水色の要素まで数珠繋ぎにしたものが図.2の上のリストです。
水色の要素のアドレスもどこかに保存しておけば、図からも分かるようにリストを後からたどっていくことができます。このように、前からも後からもたどっていくことができるリストのことを双方向リストと呼びます。これに対し、前回のように一方通行にしかたどれないリストは単方向リストと呼びます。
ここで、黄色の要素と緑色の要素の間に紫色の要素を入れることにします。先ず、紫色の要素の1つ目のポインタには黄色の、2つ目のポインタには緑色の要素のアドレスを入れます。そして、次に黄色の要素の2つ目のポインタと緑色の要素の1つ目のポインタに紫色の要素のアドレスを入れます。こうして要素の挿入が完了します。これが図.2の下のリストです。
要素を追加・削除するときに操作するポインタが増えますが、後からたどることができるという利点を考えると大したことではありません。
では、実際に双方向リストを使って挿入ソートをやってみましょう。
| プログラム |
|---|
// List2.cpp
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
struct SList
{
int value; // 値
SList* pPrev; // 前の要素
SList* pNext; // 次の要素
};
bool InitList(SList* pFirst); // 初期化
void SortList(SList* pFirst); // ソート
void DispList(SList* pFirst); // 表示
void RevDispList(SList* pFirst); // 逆から表示
void FreeList(SList* pFirst); // 解放
int main()
{
// 始めと終わりを表す特殊な要素
SList list;
srand((unsigned)time(NULL));
if(InitList(&list))
{
SortList(&list);
DispList(&list);
RevDispList(&list);
}
FreeList(&list);
return 0;
}
// リストの初期化
bool InitList(SList* pFirst)
{
bool bRet = true; // 戻り値
SList* pNew; // 新しい要素へのポインタ
SList* pPrev; // 前の要素
int i;
// i = 0 の時、pPrev は pFirst になります
// pFirst の pNext に
// 初めの要素へのアドレスを格納します
pPrev = pFirst;
for(i = 0; i < 32; i++)
{
pNew = new SList;
// メモリの確保に失敗したら、
// 要素を確保せずに終了
if(pNew == NULL)
{
bRet = false;
break;
}
pPrev->pNext = pNew;
pNew->pPrev = pPrev;
pNew->value = rand() % 256;
pPrev = pNew;
}
// ここでは pPrev が最後の要素になり、
// その pNext には pFirst を入れて終わりを示します
// そして、pFirst の pPrev に
// 最後の要素へのアドレスを格納し、
// 後ろから要素を参照していけるようにします
pPrev->pNext = pFirst;
pFirst->pPrev = pPrev;
return bRet;
}
// ソート
void SortList(SList* pFirst)
{
// 要素数が0か1のときはソート不要
if(pFirst->pNext == pFirst->pPrev)
return;
SList* pInsert; // 挿入する要素
SList* pFind; // 挿入位置
SList* pInsNext; // 次の要素
for(pInsert = pFirst->pNext->pNext; pInsert != pFirst; pInsert = pInsNext)
{
// 要素の差し替えがあるので初めに退避
pInsNext = pInsert->pNext;
for(pFind = pFirst->pNext; pFind != pInsert; pFind = pFind->pNext)
{
// 挿入位置が決まったら挿入する
if(pInsert->value < pFind->value)
{
// pInsert を一旦リストから外す
pInsert->pPrev->pNext = pInsert->pNext;
pInsert->pNext->pPrev = pInsert->pPrev;
// pInsert の左右を変更
pInsert->pPrev = pFind->pPrev;
pInsert->pNext = pFind;
// pInsert をリストに組み込む
pFind->pPrev->pNext = pInsert;
pFind->pPrev = pInsert;
// 次の要素の挿入に移る
break;
}
}
}
}
// リストの内容を表示
void DispList(SList* pFirst)
{
SList* pNow; // リストの要素
int i;
for(i = 0, pNow = pFirst->pNext;
pNow != pFirst; pNow = pNow->pNext, i++)
{
printf("%03d ", pNow->value);
if(i % 16 == 15)
putchar('\n');
}
}
// リストの内容を逆から表示
void RevDispList(SList* pFirst)
{
SList* pNow; // リストの要素
int i;
for(i = 0, pNow = pFirst->pPrev;
pNow != pFirst; pNow = pNow->pPrev, i++)
{
printf("%03d ", pNow->value);
if(i % 16 == 15)
putchar('\n');
}
}
void FreeList(SList* pFirst)
{
SList* pNow; // リストの要素
for(pNow = pFirst->pNext; pNow != pFirst; )
{
SList* pTemp = pNow->pNext; // 一時的に退避
delete pNow;
// この時点では pNow->pNext は削除されています
pNow = pTemp;
}
} |
| 実行結果例 |
009 013 021 023 029 042 068 071 071 077 123 134 151 155 169 171 172 179 180 183 184 185 186 188 191 197 200 224 226 235 246 253 253 246 235 226 224 200 197 191 188 186 185 184 183 180 179 172 171 169 155 151 134 123 077 071 071 068 042 029 023 021 013 009 |
はい。挿入法でソートを行うことができました。今回のように挿入ソートを行いたいときなどは、双方向リストを使う必要があるのです。
さらに、内容を逆順で表示することもできました。多少構造は複雑になりますが双方向リストは使い勝手がよく、よく使うことになるでしょう。
もちろん、後からたどる必要が全くない場合には単方向リストで充分です。場合によって使い分けるようにするといいでしょう。
では、今回の要点です。
何か短かったですね。こういう回もたまにはいいでしょう。ということで、また次回まで。
Last update was done on 2001.2.4
この講座の著作権はロベールが保有しています