今回は、先ずはバブルソート同様低速なソート法を考えます。しかし、それをもとにした高速なソート法も同時に紹介したいと思います。
それでは、今回の要点です。
では、いってみましょう。
今回も新しいソート法を考えてみます。今回のソート法は人間がよく使う方法です。
トランプをするとき、手札を数字の順番通りに並べることがよくあります。こういうとき、以前のバブルソート、選択法と同じように並べ替える人は少ないと思います。(そうしている人いたら、ごめんなさい。)
普通は、並んでいない部分から1枚抜き取り、並んでいる部分に大小の合うように差し込んでいくと思います。これが今回のソート法、挿入法です。
 |
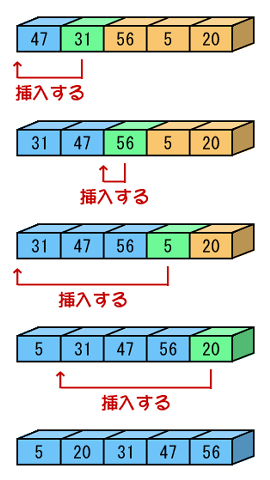
| 図.1 挿入法 |
|---|
コンピュータにやらせるときは、右の図のようにします。
先ず、初めの1要素をソートされた列と見なします。そして、2番目の要素をここに挿入します。これでこの2要素はソートされました。
次、3番目の要素をソートされた列に挿入します。これで3要素がソートされました。
あとは同じように要素をソートされた列に挿入していき、挿入するものがなくなった時点でソート完了です。
では、プログラムを見てみましょう。
| プログラム |
|---|
// Sort3.cpp
#include "SortData.h"
#include "SortSub.h"
// 挿入法によるソート
void InsertionSort(int* pnData, int nNumOf)
{
int iInsert; // 挿入する要素のインデックス
int iSwap; // 交換していくときのループ変数
// 挿入する要素のインデックスは1から始まる
for(iInsert = 1; iInsert < nNumOf; iInsert++)
{
// 挿入は順次交換することで行う
for(iSwap = iInsert; iSwap > 0; iSwap--)
{
// 順序がきちんとした時点でループを終える
if(pnData[iSwap - 1] < pnData[iSwap])
break;
Swap(pnData[iSwap - 1], pnData[iSwap]);
}
}
}
int main()
{
InsertionSort(g_anData, g_nNumOf);
DispArray(g_anData, g_nNumOf);
return 0;
} |
| 実行結果 |
1, 1, 4, 6, 9, 9, 10, 11, 13, 14, 15, 16, 23, 25, 28, 29, 31, 33, 34, 39, 39, 40, 40, 41, 42, 44, 48, 51, 51, 53, 54, 55, 56, 63, 67, 68, 73, 73, 76, 77, 78, 79, 79, 87, 89, 99, 99, 101, 101, 103, 110, 112, 116, 117, 117, 118, 124, 128, 136, 137, 137, 138, 148, 150, 152, 155, 157, 160, 161, 164, 166, 167, 168, 169, 173, 173, 174, 175, 185, 186, 188, 192, 199, 203, 213, 215, 222, 228, 228, 229, 231, 235, 239, 240, 240, 242, 249, 249, 254, 255, |
はい、きちんとソートできましたね。
確かにソートはできるのですが、これでは交換回数が多くバブルソートと大して変わりがありません。事実、速度はバブルソートと大して変わりません。乱数のソートで試したところ、データ数が少なければバブルソートの方が、多ければ挿入法の方が若干速いみたいです。
では、そんなものを何故紹介したのかというと、このソート法を元にした高速なソート法が開発されているからです。名前はシェルソートといいます。shell は「殻」という意味の単語ですが、シェルソートのシェルは開発者の名前 D.Shell から来ています。
挿入法が何故遅いのかというと、挿入位置が遠くにあった場合に沢山交換が起こるからです。
そこで先ずは離れた要素間でソートするようにすれば、極端に位置のずれた要素も少ない交換回数でソートできます。ただ、もちろんそれだけではソートは完了しません。その幅を狭めてまたソートし、それを幅が1になるまで続ければ、ソートが完了します。こうすれば、もっと交換回数を減らすことができるはずです。
これを図にすると次のようになります。
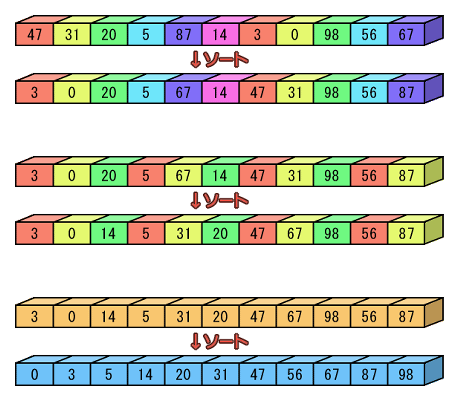 |
| 図.2 シェルソート |
|---|
先ず、一番上の列を見て下さい。ここで、同じ色の要素同士でソートをします。すると、その下の列のようになります。
で、次に分け方を変えます。同じ色の要素同士の距離が短くなっていますね。そして、また同じ色の要素同士でソートします。すると、大体大雑把にソートされていることが目に見えて分かります。
そして、最後に全体でソートをし直すと終了です。挿入法では、ソートされた状態に近いと、挿入位置が近いため処理は格段に減ります。こうして、初めは各グループの要素数が少ないので速く、後の方はソートされている位置に近くて速くなり、全体的にかなりの高速化が期待できます。
では、プログラムを見てみましょう。
| プログラム |
|---|
// Sort4.cpp
#include "SortData.h"
#include "SortSub.h"
// シェルソート
void ShellSort(int* pnData, int nNumOf)
{
int nSpan; // ソート間隔
// 初めは nNumOf / 2 だけ離れた場所の要素同士でソートする
// 以後、間隔を2分の1していき、最終的には nSpan が1になる
// 2進数で考えると分かりやすいが、最終的には nSpan は必ず1に到達する
for(nSpan = nNumOf / 2; nSpan >= 1; nSpan /= 2)
{
int iInsert; // 挿入する要素のインデックス
int iSwap; // 交換していくときのループ変数
// 各グループのソートをまとめて行う
for(iInsert = nSpan; iInsert < nNumOf; iInsert++)
{
for(iSwap = iInsert; iSwap >= nSpan; iSwap -= nSpan)
{
if(pnData[iSwap - nSpan] < pnData[iSwap])
break;
Swap(pnData[iSwap - nSpan], pnData[iSwap]);
}
}
}
}
int main()
{
ShellSort(g_anData, g_nNumOf);
DispArray(g_anData, g_nNumOf);
return 0;
} |
| 実行結果 |
1, 1, 4, 6, 9, 9, 10, 11, 13, 14, 15, 16, 23, 25, 28, 29, 31, 33, 34, 39, 39, 40, 40, 41, 42, 44, 48, 51, 51, 53, 54, 55, 56, 63, 67, 68, 73, 73, 76, 77, 78, 79, 79, 87, 89, 99, 99, 101, 101, 103, 110, 112, 116, 117, 117, 118, 124, 128, 136, 137, 137, 138, 148, 150, 152, 155, 157, 160, 161, 164, 166, 167, 168, 169, 173, 173, 174, 175, 185, 186, 188, 192, 199, 203, 213, 215, 222, 228, 228, 229, 231, 235, 239, 240, 240, 242, 249, 249, 254, 255, |
この例では分からないと思いますが、随分速くなっています。どれくらい速いかというと、10万要素の乱数列をソートしてみたところ2,3秒(MMXペンティアム300MHzで)で終わりました。同じものを生の挿入法を使ってソートすると30分くらいかかりました。
このように、高速なソートアルゴリズムは要素数の多いときに劇的に効果が現れます。遅いソート法を使っていると、それは大きな損になります。
次回はさらに高速なアルゴリズムを紹介します。速度にムラはあるものの、高速ソートアルゴリズムの代表格に君臨しています。次回を楽しみにしていて下さい。
それでは、今回の要点です。
それでは、次回まで。
Last update was done on 2000.9.20
この講座の著作権はロベールが保有しています