 |
| 図.1 木 |
|---|
今回はおそらく一番身近なデータ構造について話します。それは一体何なのでしょうか。
では、今回の要点です。
では、いってみましょう。
先ずは、次の図を見て下さい。
 |
| 図.1 木 |
|---|
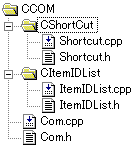
これが今回話すデータ構造である「木 (tree)」です。第23章でも少し触れましたね。
木構造はファイルシステムであまりにも有名です。エクスプローラの左ペインを見れば、木構造がどんなものかはすぐ分かるでしょう。VC++をやっていても、ワークスペースに木構造を見ることができます。
先ず、木は要素を持っています。ファイルシステムではファイルやフォルダがこれに当たります。こういった木の要素のことを「節 (ノード:node)」や「頂点」と呼びます。
そして、ノードは下にいくつか別のノードを持っていることがあります。例えば図.1では、CCOM は CShortCut, CItemIDList, Com.cpp, Com.h という4つのノードを持っています。さらに CShortCut は Shortcut.cpp, Shortcut.h を、CItemIDList は ItemIDList.cpp, ItemIDList.h を持っています。こうして木は階層的にデータを扱うことができます。次のノードのことを「子ノード」、前のノードのことを「親ノード」とも呼びます。そして、親と子を繋ぐ線を「枝 (branch)」や「辺」と呼びます。
そして、木は一番元となるノードをただ1つだけ持っています。ファイルシステムではルートフォルダがこれに当たります。図.1では CCOM に当たります。これを「根 (ルート:root)」と呼びます。反対に、子を持たないノードのことを「葉 (leaf)」と呼びます。
では、この木というデータ構造をプログラムで扱おうとするとどうなるのでしょうか?
これには前回までやったリスト構造がヒントになります。よく考えてみると、リストは子ノードが最高1つしかない木と考えることができます。ということは、次の要素へのポインタを何個も持つようにすればいいことが分かります。また、リストに単方向リストと双方向リストがあるように、木でも単方向と双方向の木を作ることができます。
今度はノードを扱う処理を考えます。やってみると分かりますが、これを普通の関数で処理しようとすると結構骨です。ある子ノードに処理を移し、そこでの処理を終えたとします。すると、親ノードに戻る必要があります。単方向なら親ノードが何かを保存しておく必要があります。深く潜っていくことを考えると、これは配列かリストかなどに保存する必要があります。もしくは、ノードに含ませておく必要があります。また、親に戻ったところで次に処理するべき子ノードがどれかというのが分かりません。これも保存しておく必要があります。
しかし、ここで考えて下さい。そのノードにあるデータをいつ扱うかは状況によるので何とも言えませんが、とにかく子ノードに対しても同じ処理を行っていく事は確かです。そうです。どのノードも全く同じ処理が適用できるということで、再帰関数が使えそうです。親ノードは引数で渡し、ノードの処理の順番を管理する変数は内部変数におけばいいですね。引数も内部変数も呼ぶたびに新しいものができるので、その値の保存に関しては何の問題もありません。再帰関数を使えば、木を何の苦もなく扱うことができるのです。
簡単な例として子ノードを最大2つまでしか持たない木を考えてみましょう。このような木のことを二分木 (binary tree) と呼びます。二分木という名前が付いているからには、いろいろな用途があります。例えば、次の章で話す二分探索木や第29章で少し触れたヒープソートなどに使われます。(注:ヒープソートは配列を木と見なして扱うだけなので、ノードはポインタを持つとは限りません。)
では、次の図を見て下さい。
 |
| 図.2 二分木 |
|---|
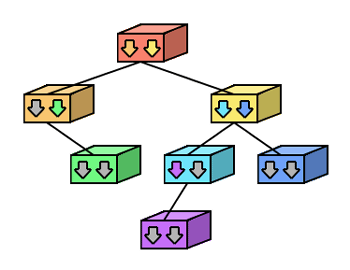
赤色のノードがルートになります。各ノードは2つのポインタを持っており、赤色のノードは橙色のポインタと黄色のポインタを持っています。つまり、赤色のノードは橙色と黄色の2つの子ノードを持っています。
橙色のノードもまた子ノードを持っています。しかし、1つしか子ノードを持っていません。左側の矢印は灰色になっており、ポインタには子ノードがないことを表す特殊な値を入れることになります。一方黄色のノードは水色と青色の2つのノードを持っています。同様に水色のノードも紫色の子ノードを持っており、これで木は終わりです。葉は緑色、青色、紫色の3つになります。
では、この二分木を使って何かやってみましょう。ある数値と別の数値を関連付けるプログラムでも作ってみます。
1つ目の数値のビットを元にどちらのノードを進むかどうかを決めます。例えば12、つまり(1100)2で考えてみます。0は特別な場所を示すことにすると、それ以外では一番上のビットは必ず1です。先ずはこの1を探します。次に、この一番上の桁から下の桁へたどっていきます。この例では1、0、0ですね。0を左、1を右と考えると、右、左、左と解釈できます。この通りに木をたどっていったところに2つ目の数値を関連付けます。図.2の紫色のノードにあたりますね。
同じように考えると、赤色のノードは1、橙色のノードは2、黄色のノードは3、緑色のノードは5、水色のノードは6、青色のノードは7になります。
では、実際にプログラムしてみましょう。
| プログラム |
|---|
// Tree1.cpp
#include <iostream.h>
#include <iomanip.h>
// 二分木のノード
struct SNode
{
int value; // 値
SNode* pNext[2]; // 子ノード
};
// 二分木
struct STree
{
int value; // 値
SNode* pRoot; // ルート
};
// 初期化処理
void InitTree(STree* pTree);
void InitNode(SNode* pNode);
// キーのビット数
const unsigned KEY_BITS = sizeof (unsigned) * 8;
// 最上位ビット
const unsigned TOP_BIT = 1 << (KEY_BITS - 1);
// ノードを追加
void AddNode(STree* pTree, unsigned key, int value);
// ノードを追加(再帰サブルーチン)
SNode* Rec_AddNode(SNode** ppParent, unsigned key, int nBit);
// 木を削除
void FreeNode(STree* pTree);
// 木を削除(再帰サブルーチン)
void Rec_FreeNode(SNode* pParent);
// 木全体を表示
void DispTree(STree* pTree);
// 木全体を表示(再帰サブルーチン)
void Rec_DispTree(SNode* pParent, int nDepth);
// データ入力
bool Input(STree* pTree);
int main()
{
STree tree;
InitTree(&tree);
while(Input(&tree));
DispTree(&tree);
return 0;
}
// 木の初期化
void InitTree(STree* pTree)
{
pTree->value = 0;
pTree->pRoot = NULL;
}
// ノードの初期化
void InitNode(SNode* pNode)
{
pNode->value = 0;
pNode->pNext[0] = NULL;
pNode->pNext[1] = NULL;
}
// ノードを追加
void AddNode(STree* pRoot, unsigned key, int value)
{
// 0の場合
if(key == 0)
{
pRoot->value = value;
return;
}
int nBit; // ビット番号
// 最上位ビットに「1」を持ってきます
for(nBit = KEY_BITS - 1; (key & TOP_BIT) == 0; nBit--)
key <<= 1;
//
SNode* pAdd = Rec_AddNode(&pRoot->pRoot, key, nBit);
if(pAdd != NULL)
pAdd->value = value;
}
// ノードを追加(再帰サブルーチン)
// 戻り値は追加された要素のアドレスです
SNode* Rec_AddNode(SNode** ppParent, unsigned key, int nBit)
{
// 要素の確保
if(*ppParent == NULL)
{
*ppParent = new SNode;
if(*ppParent == NULL)
return NULL;
InitNode(*ppParent);
}
// 追加した要素のアドレスを返します
if(nBit == 0)
return *ppParent;
key <<= 1;
SNode** ppNext = &(*ppParent)->pNext[(key & TOP_BIT) != 0];
// 次のノードへ
return Rec_AddNode(ppNext, key, nBit - 1);
}
// 木を削除
void FreeNode(STree* pTree)
{
if(pTree->pRoot != NULL)
Rec_FreeNode(pTree->pRoot);
}
// 木を削除(再帰サブルーチン)
void Rec_FreeNode(SNode* pParent)
{
int i;
for(i = 0; i < 2; i++)
{
SNode* pNext = pParent->pNext[i];
if(pNext != NULL)
Rec_FreeNode(pNext); // 子以降を削除します
}
delete pParent; // 最後に自分を削除します
}
// 木全体を表示
void DispTree(STree* pTree)
{
cout << pTree->value << endl;
Rec_DispTree(pTree->pRoot, 0);
}
// 木全体を表示(再帰サブルーチン)
void Rec_DispTree(SNode* pParent, int nDepth)
{
if(pParent == NULL)
return;
int i;
// setw で表示幅を指定できます
// iomanip.h をインクルードしてから使います
cout << setw(nDepth * 2) << "" << pParent->value << endl;
for(i = 0; i < 2; i++)
Rec_DispTree(pParent->pNext[i], nDepth + 1);
}
// データ入力
bool Input(STree* pTree)
{
unsigned key;
int value;
cout << "数値を2つ入力して下さい > " << flush;
cin >> key >> value;
if(value == -1)
return false;
AddNode(pTree, key, value);
return true;
} |
| 実行結果例 |
数値を2つ入力して下さい > 1 1
数値を2つ入力して下さい > 2 2
数値を2つ入力して下さい > 3 3
数値を2つ入力して下さい > 5 4
数値を2つ入力して下さい > 6 5
数値を2つ入力して下さい > 7 6
数値を2つ入力して下さい > 12 7
数値を2つ入力して下さい > 0 -1
0:0
2
4
1
7
5
3
6 |
図.2と同じ配置で表示されるように入力してみました。上が左に、下が右にくるように反転して見ます。1〜7が赤〜紫に対応していると考えて下さい。
このように、木を使えばデータを階層的に扱うことができるようになります。
では、今回の要点をもう一度見てみましょう。
次は上で予告通りの内容になります。それでは。
Last update was done on 2001.2.6
この講座の著作権はロベールが保有しています