 |
| 図.1 リスト |
|---|
今回からはデータ構造に関する話に入っていきます。手始めに、リストに関して話したいと思います。
では、今回の要点です。
では、いってみましょう。
挿入ソートで配列に要素を挿入するとき、挿入する場所まで要素を交換し続けるという面倒な事をしました。配列は「途中に挿入する」ということには弱いわけです。同じく、「途中の要素を削除する」ということにも弱いです。
あまり「挿入」や「削除」という操作を行うことがない場合はこれで問題ありませんが、頻繁に挿入や削除を行いたいようなデータではちょっと不便ですね。そういう場合は、データをリストにすると便利です。
では、その「リスト」とは一体何なのでしょうか? 先ずは下の図を見て下さい。
 |
| 図.1 リスト |
|---|
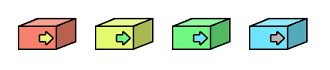
一番上に4つの要素が並んでいます。この要素の1つ1つは構造体またはクラスです。
要素の中に矢印が描いてありますが、これは次の要素へのポインタです。つまり、リストというのは次の要素へのポインタを持たせることでデータを数珠繋ぎにしたものということになります。
先ず初めに赤色の要素があります。そして、そのメンバに次の要素へのポインタがあります。矢印は黄色ですから、次の要素は黄色の要素になります。次に黄色の要素があります。そこにある矢印は緑色の矢印なので、次の要素は緑色の要素になります。同じように次の要素は水色の要素となり、ここで矢印はリストの終わりを示す灰色の矢印になっていて、これが最後の要素になります。リストの終わりを示すには、実際には NULL ポインタか、終わりを示す特別な実体のアドレスを使うことになります。
このように、赤色の要素の位置さえ分かっていれば、たとえ赤色、黄色、緑色、水色の要素がメモリ上でバラバラに存在していたとしても、全部の要素を参照することができるわけです。
では、この黄色の要素と緑色の要素の間に紫色の要素を挿入したいと思います。こういう場合、どうしたらいいと思いますか?
そうですね。緑色の要素へのポインタを紫色の要素に、そして紫色の要素へのポインタを黄色の要素に持たせればいいわけです。
このとき、紫色の要素はメモリ上のどこにいても構わない点に注意して下さい。これを図で描くとこうなります。
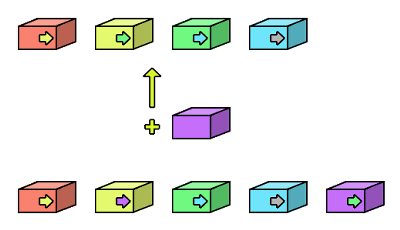 |
| 図.2 リストへの挿入 |
|---|
こうしておけば、赤色、黄色、紫色、緑色、水色の順で要素を参照していくことができるわけです。
また、途中の要素の削除も簡単です。紫色の要素を削除したいときは、黄色の要素にある次の要素へのポインタに、紫の要素内にある同じポインタの値を代入すればいいだけです。(もし紫色の要素を動的に確保していれば、delete する必要があります。)
では、ちょっと例を見てみましょう。
| プログラム |
|---|
// List1.cpp
#include <iostream.h>
#define numof(array) (sizeof (array) / sizeof *(array))
// 色を表す文字列
static const char g_asColor[][3] = {
"赤", "橙", "黄", "緑", "青", "藍", "紫",
};
// 色の上限、下限値
const int COL_FIRST = 0;
const int COL_LAST = numof(g_asColor) - 1;
// 色を保持するリストの要素
struct SColor
{
int color; // 色
SColor* pNext; // 次の要素へのポインタ
};
// 最初の要素のアドレスを保持する特別な要素
static SColor g_ColFirst = { 0, NULL };
// index で示す位置に色を挿入
bool InsertColor(int index, int color)
{
SColor* pNew = new SColor; // 動的に要素を確保する
if(pNew == NULL)
return false;
pNew->color = color;
SColor* pOld; // 要素を挿入する位置
int i;
// index の位置に来るか、最後に来るかしたら、そこへ挿入します
// 分かりづらければ0〜2個の要素で考えてみて下さい
for(i = 0, pOld = &g_ColFirst;
i < index && pOld->pNext != NULL; i++)
{
pOld = pOld->pNext;
}
// 挿入
pNew->pNext = pOld->pNext;
pOld->pNext = pNew;
return true;
}
// リストを解放
void Release()
{
SColor* pDel = g_ColFirst.pNext;
while(pDel != NULL)
{
// delete したあとに pDel->pNext を取得してはいけません
SColor* pNext = pDel->pNext;
delete pDel;
pDel = pNext;
}
g_ColFirst.pNext = NULL;
}
// 入力と挿入
bool Input()
{
int index;
int color;
cout << "何色にする?"
"(0123456→赤橙黄緑青藍紫)> " << flush;
cin >> color;
if(color < COL_FIRST || COL_LAST < color)
return false;
cout << "何番目に挿入する? > " << flush;
cin >> index;
if(index < 0)
return false;
// 色を挿入
if(!InsertColor(index, color))
return false;
return true;
}
// リストの内容を表示
void DispColors()
{
SColor* pColor = g_ColFirst.pNext;
while(pColor != NULL)
{
cout << "色:" << g_asColor[pColor->color]
<< " , アドレス:" << pColor << endl;
pColor = pColor->pNext;
}
}
int main()
{
while(Input());
DispColors();
Release();
return 0;
}; |
| 実行結果例 |
何色にする?(0123456→赤橙黄緑青藍紫)> 0 何番目に挿入する? > 0 何色にする?(0123456→赤橙黄緑青藍紫)> 2 何番目に挿入する? > 1 何色にする?(0123456→赤橙黄緑青藍紫)> 3 何番目に挿入する? > 2 何色にする?(0123456→赤橙黄緑青藍紫)> 4 何番目に挿入する? > 3 何色にする?(0123456→赤橙黄緑青藍紫)> 6 何番目に挿入する? > 2 何色にする?(0123456→赤橙黄緑青藍紫)> 7 色:赤 , アドレス:0x00022078 色:黄 , アドレス:0x00022088 色:紫 , アドレス:0x000220B8 色:緑 , アドレス:0x00022098 色:青 , アドレス:0x000220A8 |
リストを使えば、挿入操作はポインタの代入2回だけですみます。配列では後の要素を全部ずらしていく必要があるのに、これは大きな差です。
そして、要素を1つずつ動的に確保していっても順番を保つことができます。可変長配列メンバをもつ構造体のように1つ1つの要素の大きさが違っていても、全く問題ありません。
では、最後にポインタの配列とリストとの比較を行ってみます。
ポインタの配列を使う利点は、インデックスを使って簡単に要素を参照できるというところです。リストを使うと、上の InsertColor 関数のように使うたびに for 文で数えていく必要があります。このため、リストには二分探索は使えません。ソートには挿入ソートが使えますね。
一方ポインタの配列を使う欠点は、挿入に無駄が多いというところと、もう1つ自由な拡張がしにくいところにあります。ポインタの配列を使ってしまうと、その配列のサイズを気にする必要があります。配列のサイズを超えるような場合には、配列を再確保する必要がありますね。再確保するということは、新しい配列を用意して、さらに、前の配列を全てコピーしてこなくてはなりません。ここに無駄が生じます。
このように、リストも配列も一長一短であり、データを扱うときはどちらを使ったらいいか考える必要があります。
では、今回の要点です。
次回もリストです。しかし、ちょっと違います。それでは。
Last update was done on 2000.12.25
この講座の著作権はロベールが保有しています