地図投影法を理解するには、まず地球の形と見方について学ぶ必要があります。

• 地球の大きさ
• 経度と緯度
• 方位角
• 大圏コース
• 航程線

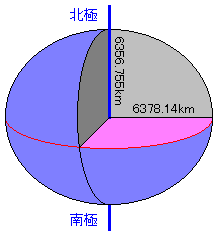
古代ギリシアの時代から地球が球体であることは知られていましたが、正確にはわずかに上下に潰れています。これを「回転楕円体」といい、楕円形を短軸に沿って回転させたときにできる図形です。地軸が短軸にあたります。自転の影響によるものと考えられています。 地球の大きさを正確に定義することは実はとても難しいことです。地球の表面には凹凸があり、近似する回転楕円体を設定しなければならないためです。このため19世紀から現在までいろいろな値が発表されてきました。1976年の国際天文学連合によれば、短軸つまり北極から地球の中心までの距離は 6356.755km で、長軸つまり赤道の半径は 6378.140km です。その差は 21.385km 、扁平率にすると 1/298.26 と、非常に小さな値なので、縮尺の小さな地図では球体とみなしてもさしつかえありません。回転楕円体による投影は計算が非常に複雑なため、多くの投影法は地球を球体とみなして計算式を導き出しています。 PTOLEMYではより新しいモデルであるGRS80から導いた球体半径を採用しています。こちらは赤道半径が 6378.137km、極半径が 6356.752km、扁平率は 1/298.257222101 で、この楕円体と同じ体積の球体の半径は 6371.00078997414km です。

（図：地球楕円体）

地球上の位置は「経度」と「緯度」を用いた座標で表現されます。経度は東西方向の角度で、本初子午線を中心にして西経180度から東経180度までで表します。緯度は南北方向の角度で、赤道を中心にして南緯90度から北緯90度までで表します。ある地点の座標は“北緯12度34分50秒、西経123度45分01秒”、あるいは“南緯12度34分、東経123度45分”のように表現します。

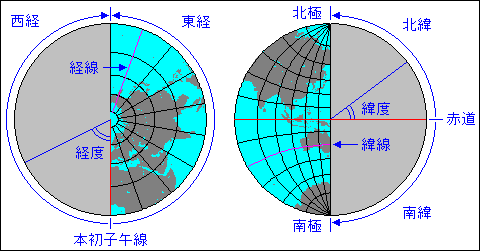
経度を同じくする地点を結んだ線、つまり南北方向に想定して地図上に表示された線を「経線（meridian）」といいます。経線は北極から南極までで、地球を半周します。地球上ではある地点を通る経線を「子午線」ということもあります。イギリスのグリニッジ天文台跡を通る子午線を特に「本初子午線」といい、ここを経度０とします。

緯度を同じくする地点を結んだ線、つまり東西方向に想定した線を「緯線（parallel）」といいます。緯線は地球を一周し、赤道から離れるにつれて全長は短くなります。

（図：経線と緯線で地表を区切る）

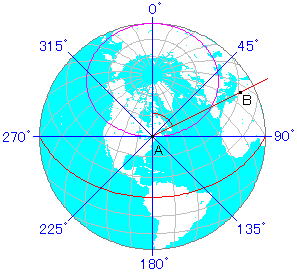
方位角とは地球上でＡ点からみたＢ点の方向を表わす角度です。Ａ点とＢ点を結ぶ大圏コースが、Ａ点を通る経線と交わる角度のことをいいます。北を0度として時計周りに計ります。Ａ点を中心にした方位図法では、すべての方位を直線で表すことができます。ここで注意してほしいのは、赤道上以外ではＡ点とＢ点が同じ緯度でも方位角は90度あるいは270度にはならない点です。 ただしこれは方位角の場合です。日常生活においては、古くからの慣習や円筒図法で描かれた地図の影響が強いため、東西を緯線に沿うものとみなすこともあります。混乱を避けたいときは、東西南北ではなく、方位角で表記してください。

（図：北緯45度での方位角）

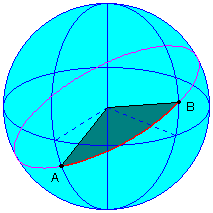
地球上の２つの地点を結ぶ最短通路（地表を通って）のことを大圏コースといいます。このコースを延長して地球を一周すると、それによってできる円の中心は地球の中心と一致します。つまり大円にあたるわけで、大円コースともいいます。心射方位図法を使うとすべての大圏コースを直線で表すことができます。そのほかの投射方位図法でも、一方が投影中心の場合に限り直線で表わすことができます。

（図：赤線はＡ点とＢ点を結ぶ大圏コースでピンクは大円）

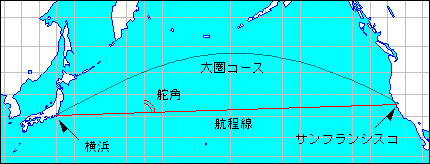
ある地点から他の地点へ行くとき、経線と常に一定の角度で交差しながら進んでいくコースを航程線といいます。経線となす角度を舵角といい、航海ではコンパスをみながら舵角方向へ進めば目的地へ到達することができます。等角航路ともいいます。２点が同経度、あるいは赤道上にない限り、大圏コースとは一致せず、距離も長くなります。メルカトル図法で投影すると、航程線を直線で表すことができます。

（図：メルカトル図法における航程線と大圏コース。横浜からサンフランシスコまで）