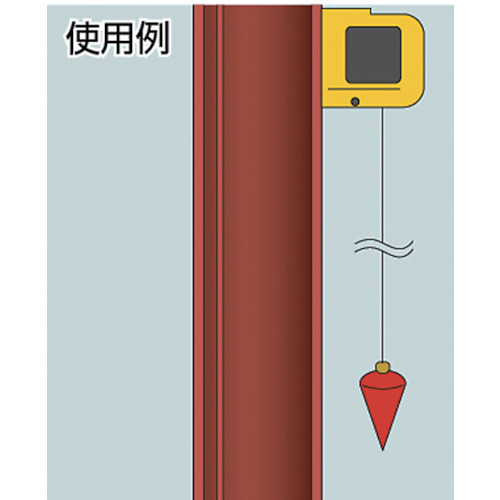
フーコーの振り子は静止しない　 

（2021年2月21日） 　フーコーの振り子は地球の自転を証明したことで有名です。このブログでも2回も書きました。 　小型のフーコー振り子 　科学博物館でフーコーの振り子を観察 　フーコーの振り子がどういう物かは上の二つで分かると思います。フーコーの振り子は振り続けることに意味があるのです。 　しかし、フーコーの振り子は最初に振幅を与えなければ何時までも静止しているのでしょうか。常に鉛直方向という固定された方向を示したままなのでしょうか。  大工さんが使う道具に柱を鉛直に立てたかを確認する下げ振りがあります。 　　　　　　　　　　　　　　　図１　下げ振りの使用例   　地球の重力場で示される重力の方向は常に地球の重心に向いています。従って、地球の自転に伴って重力場も自転しています。このため振り子の錘は常に下にあって天井にぶつかることはありません。 　地球の重力を構成するのは主として万有引力と地球の自転による遠心力です。このことは国土地理院のホーム頁にも書かれています。 https://www.gsi.go.jp/buturisokuchi/grageo_gravity.html 　重力に影響しているのはこの他に、太陽と月の重力があります。これらが地球の重力に対して無視できないほどのものであることは地球の海に潮汐現象があることでも確かです。 　潮汐現象は太陽より月の方が影響が大きいのですが、これは月の方がずっと近いためです。地球の表面に作用する重力は月の重力より太陽の重力の方が200倍ぐらい大きいのです。 　太陽は朝に東から上り、夕方に西に沈みます。これは太陽の重力が地球に対しては方向が常に変わっているということになります。 　地球の重力の方向は常に地球の重心を向いているわけではないということになります。するとフーコーの振り子に対して重力の方向はいつも揺らいでいることになるでしょう。建物自体は地表に固定されていますからフーコーの支点は地球に対して静止していると考えられますが、振り子の錘は揺らぐことになります。 　地表における太陽の重力の大きさは主たる重力の6/10000ぐらいです。上野の科学博物館のフーコーの振り子の長さは20mありますから、静止させた積りでも、1日で観察すると静かに動き、朝に1.2�p東に夕方に1.2cm西方向に動くでしょう。 　錘は50kgもの質量がありますから多少の空気の揺れは影響しないでしょう。錘の下にボールペンでもつけて紙にあてて1日観察すれば実証できるでしょう。 　下げ振りは正しく鉛直を示しているのでしょうか。厳密には朝と夕方とで差がありますが、まあ誤差範囲でしょう。  （計算メモ） 太陽の質量 Mo：　2.0 × 1030　ｋｇ 地球の質量 ME：　6.0 × 1024　ｋｇ　　 月の質量 ＭL：　　7.4　×　1022　ｋｇ 地球と太陽の距離　ＡＵ：　1.5　×　1011　ｍ　 地球の半径　RE：　6.4　×　106　　　　ｍ 地球と月の距離　RL：　　3.8　×　108　　　　ｍ 万有引力定数　G：　6.7　×　10-11　　ｍ3ｋｇ-1ｓ-2　　　　 地球の重力（加速度）　ｇ＝ＧME／RE2　＝6.7×6.0／6.42　×10　＝9.8　ｍｓ-2 太陽の地球表面での重力　ｇS＝GMo／AU2　＝6.7×2.0／1.52　×10-3　　＝　6.0　×　10-3　ｍｓ-2　 月の地球表面での重力　　ｇＬ＝GＭL／RL2　＝6.7×7.4／3.82　×10-5　　＝　3.4　×　10-5　　ｍｓ-2　　　 ｇS／ｇ　＝6.0×10-3/9.8 ＝　6.1×10-4　　 振り子の長さl＝20　ｍ 太陽による振り子の移動量　20×6.1×10-4＝　　1.2×10-2　ｍ　（＝1.2 �p） （了） 戻る