時空の次元とコンパクト化

Last Update： 11/14/2012

　我々の住んでいる時空は、3次元空間です。ところが、超ひも理論ではしばしば9次元や10次元の空間が基本的であると考えられています。余分な次元はどうなっているのかというと、我々の現在の技術では感知できないほど小さい大きさに丸まっていると考えられています。このことを「コンパクト化」と言います。

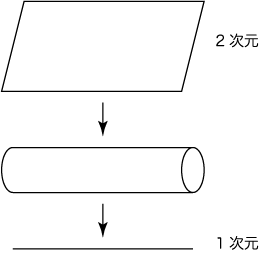
　コンパクト化というのは、「いらない」次元を処理するための単なるごまかしではありません。コンパクト化には大きな利点があります。自然界のいろいろな素粒子をまとめることもできるのです。簡単な例として、光を考えてみましょう。5次元時空の光をコンパクト化すると、光と「スカラー場」と呼ばれる粒子をまとめて考えることができます。これをストリングを使ってみてみましょう。

　さきにみたように、超ひも理論では、光は「端のあるストリング」の最も低い振動であらわされます。5次元時空の光でも、その事情は変わりません。しかし一つの次元、5次元方向が小さく丸まっているときに、ストリングが振動するとどうなるでしょう？

　このストリングは、丸まっていないふつうの3次元空間で振動することもあるでしょう。これは、これまで同様4次元時空の光をあらわしています。

しかし、ストリングは丸まっている方向に振動することもあるはずです。ところが、3次元の観測者には丸まっている方向の振動は見えません。すると、この観測者には、ストリングが振動していないように見えるでしょう。

ストリングの違う振動は、それぞれ別の素粒子をあらわします。ストリングが振動していないように見える場合は、どんな素粒子なのでしょうか？

　光は偏光という性質をもち、それはストリングの振動と考えられました。しかし、「偏光」は光だけが持つ性質ではありません。素粒子はみんな同じような性質を持っています。その特別な場合として、偏光の性質を持たない粒子もあります。この偏光の性質を持たない粒子のことを「スカラー場」と言います。ストリングが振動していないように見える場合は、このスカラー場の性質に一致します。

　まとめると、5次元時空のストリングによって、

• 3次元空間で振動するストリング → 偏光という性質をもつ → 光
• 5次元方向で振動するストリング（3次元空間で振動していないストリング）→ 偏光という性質をもたない → スカラー場

と2種類の素粒子をまとめることができます。

　なお、超ひも理論には「ループ状のストリング」もあります。超ひも理論によると、ループ上のストリングは、重力をあらわします。このループ上のストリングをコンパクト化すると、今度は

• 重力
• 光
• スカラー場

の3種類が出ることも知られています。

　ちなみに、コンパクト化はカルツァ・クライン・コンパクト化とも呼ばれます。この名前の通り、コンパクト化を提案したのはカルツァとクラインです。ところが、実はコンパクト化の発見者はフィンランドのノルドストリュームです。ノルドストリュームは、光のコンパクト化から出てくるスカラー場を使って、重力を説明しようと考えたようです。このようにして、ノルドストリュームは光と重力を統一的に説明しようと考えました。

　ノルドストリュームは、電荷を帯びたブラックホールである「ライスナー・ノルドストリューム解」も発見しました。これは現実のブラックホールを表すわけではありませんが、理論的には大変興味深く、今でも盛んに研究されています（「蒸発するブラックホール」参照）。

より詳しいコメント：
　コンパクト化された次元の大きさについては、はっきりわかっていませんが、標準的にはストリング長さ（約10^-34m）と大統一理論のスケール（約10^-32m）のあいだだと考えられています。「大統一理論」とは、自然界の4つの力のうち重力以外の力（電磁気力、弱い力、強い力）を統一すると考えられている理論です。