Top page (correct Bohr model, and Quantum mechanics is wrong. )
Spintronics of condensed matter is an illusion.
Mechanism of useless quantum chemistry
Condensed matter physics is ancient ruins.
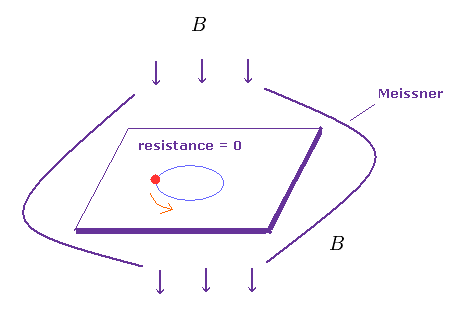
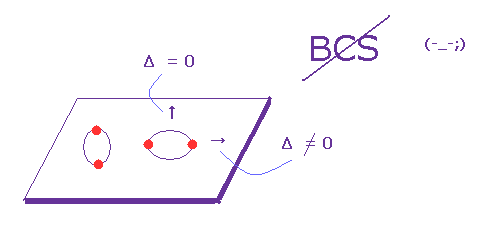
(Fig.1) Superconductor.

All the current quantum mechanical methods such as BCS (= allegedly the mainstream theory for explaining superconductors ) for condensed matter rely on unphysical quasiparticle model, so useless forever.
Superconductivity is a phenomenon of zero electrical resistance and and expulsion of external magnetic fields in some materials when they are cooled below their critical temperature (= Tc < 30 K ← almost absolute zero ).
As shown on this page, this ejection of magnetic field is called "Meissner effect", which can be explained by classical electromagnetism, Not by the failed mainstream quantum theory = BCS theory.
BCS theory is known to disagree with many experimental results such as high-temperature superconductors ( this p.26, this p.5-conclusion, this 3rd-paragraph ), so the quantum mechanical prediction turned out to be wrong.
(Fig.2) "Phonon" can attract two electrons ?
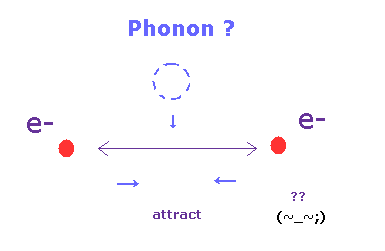
According to the standard theory (= BCS theory ), electrons are held together in Cooper pairs (= Bose particle ).
Surprisingry, though both two electrons have negative charges, these electrons attract each other, they insist.
This attraction is purportedly caused by quasiparticle "( unreal virtual ) phonons".
They insist "phonon" is also a fermion, like electrons. Of course, this phonon does NOT exist.
They say this unreal particle, "phonon" is some lattice vibration of nuclei and electrons.
But they NEVER try to clarify what this phonon really is, which attitudes (= Shut up and calculate ! ) clearly obstructs the development of condensed matter physics, forever.
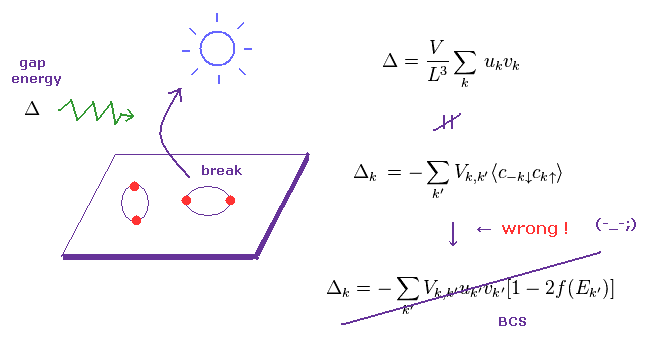
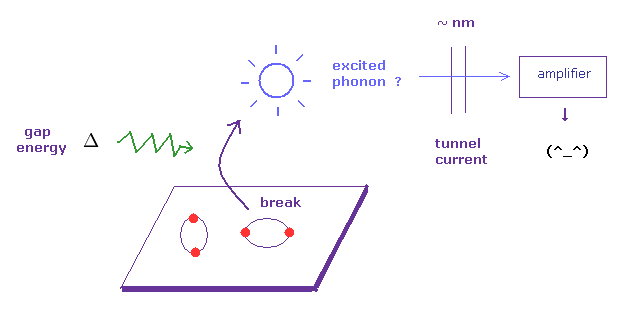
(Fig.3) Giving "gap energy" (= Δ ) to superconductor → break.
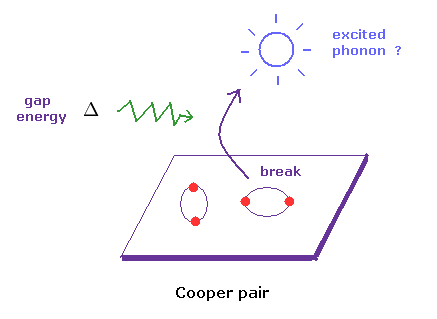
According to BCS theory, there is some "energy gap" (= Δ ) between superconducting and normal states.
So if you give some gap energy to superconductor, it generates excited phonons (= fictitious quasiparticle, this p.2 ), which can be detected, they insist.
Of course, unreal particle "phonons" themselves cannot be detected, because they are unreal.
They just detect some electric currents of electrons.
In spite of this fact, why they try to blindly believe this vague existence of "phonon" ? This is strange.
(Fig.4) Only electrons ( NOT including nuclei ! ) can attract each other ?? ← Impossible.
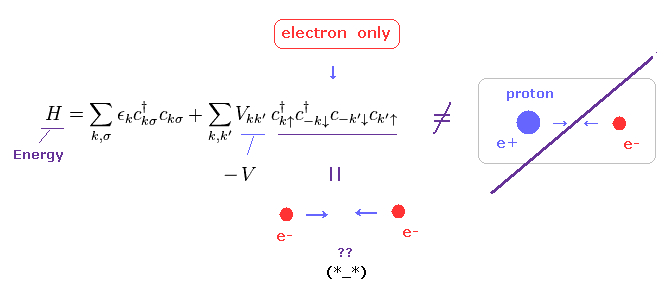
They never try to clarify mysterious force of Pauli exclusion principle.
So all we can use is very abstract mathematical creation (= c† ) and annihilation (= c ) operators to express some particles ( this p.2~ ).
As you see in Fig.4, it is almost impossible to describe various complicated actual phenomena by using only these abstract symbols.
The important point is that potential energy (= V ) in BCS theory does NOT contain positive nuclei.
There are only negative electrons (= c†, c ) in this Hamiltonian (= total energy ).
How can they attract each other without positive nuclei ? Impossible.
So this potential energy V is unrealistic and cannot be measured in the actual experiments.
As a result, this unrealistic assumption makes it difficult to develop the current theory into more complicated high temperature superconductivity, in which BCS theory breaks down.
(Fig.5) Artificial mathematical definition = Quasiparticle.
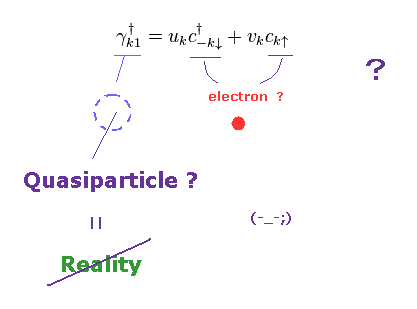
In fact, the phonon is NOT a natural concept at all.
It was introduced by using very artificial definitions.
As shown in Fig.5, besides this unreal phonon, BCS theory needs other quasiparticles (= Bogoliubov quasiparticle fermion, this p.2~, this p.4~ ).
It is strange that the creation operator (= γ† ) is the sum of creation (= c† ) and annihilation (= c ) of electrons.
So this "quasiparticle" doesn't exist, which was introduced only for getting some values close to experimental ones.
(Fig.6) ↓ Energy gap ?
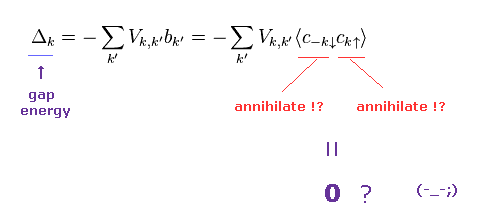
They insist the conventional BCS theory predicts various experimental values except for strongly-correlated and high temperature superconductors.
The most important concept which BCS can predict is "energy gap" = Δ.
But as shown in Fig.6, this energy gap is very unnatural.
Because it consists only of two annihilation operators ( this p.2-3 ), which is completely different from usual quantum field theory.
( Of course, there are NO clear reasons why they choose this form as energy gap. )
Again, this artificial form of Δ was introduced only for getting values close to experimental ones.
Furthermore, they use two different contradictory forms as this energy gap, as I explain later.
So BCS theory is completely wrong, not only physically but also mathematically.
(Fig.7) Temperature dependence (= curve ) of energy gap shows BCS theory is right ?
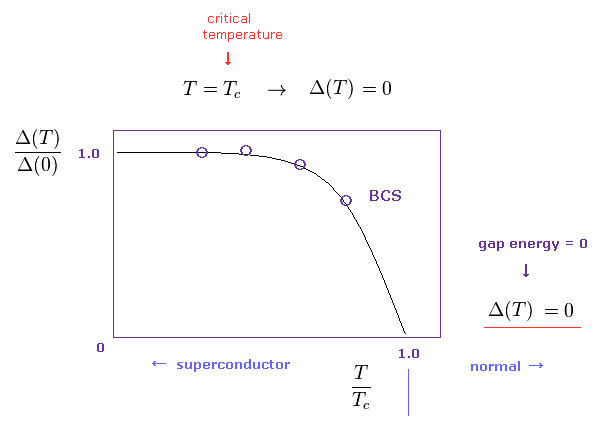
They insist BCS theory can predict correctly temperature dependence of energy gap, as shown in Fig.7.
Energy gap Δ(T) decreases as temperature (= T ) becomes higher.
And at critical temperature (= Tc ), this energy gap becomes zero.
This energy gap is specific to superconductor, so, energy gap remains zero in normal states above critical temperature, according to BCS theory.
As I explain later, this curve of Fig.7 is introduced "intentionally" ( NOT natural result of BCS theory ).
(Fig.8) Pseudogap energy also in normal state → BCS theory breaks down.
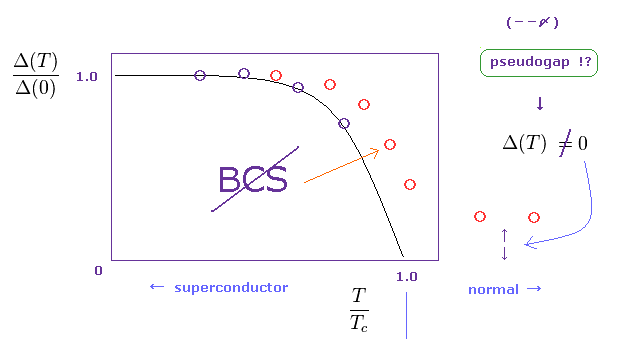
Unfortunately, they have found a lot of superconducntors in which convencional BCS theory doesn't apply.
One of them is pseudogap energy in normal state.
As I said in Fig.9, energy gap means some barrier between superconducting and normal states.
So in normal state, this energy gap must NOT exist, if the standard theory is right.
But in various materials, they found some energy gap exists also in normal conducting states.
Furthermore, in these strange superconductors, the relation between gap and critical temperature like Fig.7 is NOT satisfied. ( See red circles of Fig.8. )
So, BCS theory ( depending on unreal "phonon" ) has already failed.
(Fig.9) Energy gap (= Δ ) varies in different directions.
As shown in Fig.7, BCS theory insists energy gap depends on critical temperature universally in all materials.
But in various superconductors, this energy gap changes in different directions at the same temperature.
This is called "anisotropic" energy gap.
In these materials, there are some points where energy gap becomes zero, though it's not zero at different points.
This is called "node".
They try to introduce new concepts such as "d wave" or "p wave" superconductivity.
But this anisotropy clearly proved the conventional BCS theory already breaks down.
(Fig.10) Various materials do NOT obey BCS theory.
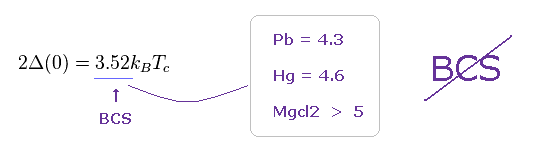
The most important and famous relation, which BCS theory predicts is the relation between energy gap (= Δ(0) ) at T = 0 and the critical temperature (= Tc ).
The ratio of "3.52" in Fig.10 is BCS's prediction.
But BCS theory relies on various rough approximations, as I explain later.
So these predictions by BCS are not so correct also in conventional superconductors ( this p.3-4 ).
As shown in various superconductors such as Pb, Hg, and Mgcl2 ..., these values becomes bigger than BCS's predictions.
(Fig.11) The relation of specific heat does NOT satisfy BCS theory.
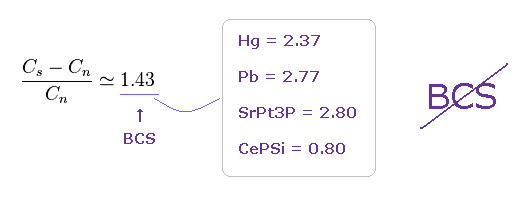
The ratio of specific heats in normal (= Cn ) and superconducting (= Cs ) states becomes "1.43" according to BCS theory.
But also in this ratio, various superconductors give different values such as 2.37, 2.8, 0.80 .. ( this p.5 )
So BCS theory based on unreal "phonon" doesn't apply in various materials.
(Eq.1) Intentional mistake in calculation → BCS theory is wrong.
As I said, the concept of energy gap (= Δ ) is the most important value which BCS can predict.
So whether BCS theory is fake or not completely depends on the definitions of this energy gap.
In fact, they make a intentional mistake in calculation, when they determine the form of this energy gap.
They need to use two different forms of energy gap to get the ratio of Fig.10.
( Of course, these forms of Δ themselves are NOT natural ones. )
The transformation from the middle to lowest equations are wrong, as I say in Trick-1.
This is the essence of BCS's trick.
(Trick-1) Trick = Deleting some terms unneeded for BCS theory.
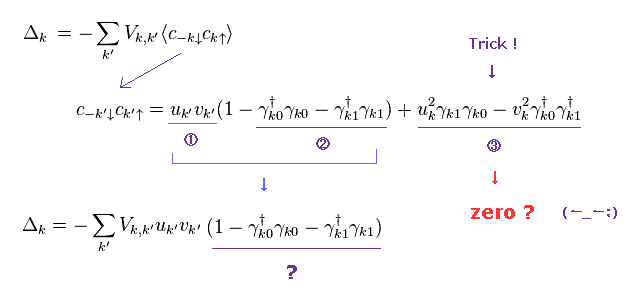
Like Fig.5, we create virtual quasiparticle (= γ ) from electrons (= c ).
As a result, energy gap Δ becomes Trick-1 middle.
Here they suddenly delete the last two terms (= 3 ). ← Trick !
As far as I see some websites and textbooks, there are NO reasonable reasons about this artificial manipulation.
( Most textbooks seem to hide this important trick ... )
I explain these things in the latter sections in detail.
(Trick-2) Trick = Replacing only specific "c" terms by γ (= quasiparticle ).

In Trick-2, they replace only "c" and "c†" terms of red line with quasiparticle (= γ ).
On the other hand, "c†" of the last term remains the original (= blue line = "b*" ), and is NOT replaced by quasiparticle.
This new operator "b*" is clearly introduced for hiding this artificial trick, I think.
( So they try to ignore ONLY the last term of Trick-2. This is strange. )
This means they intentionally choose some convenient terms for BCS theory.
Artifiicial choice of some terms is clearly one of important tricks, and shows BCS theory is unnatural and wrong.
(Eq.2)
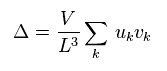
First they define the energy gap at absolute zero ( T = 0 ), like Eq.2.
"V" is the constant value, which means the magnitude of interaction energy among electrons.
"u" and "v" are some real numbers.
L is the length of one side.
(Eq.3)
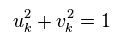
They define "u" and "v" like Eq.3 and Eq.4.
(Eq.4)
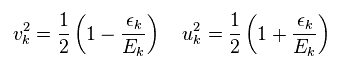
where
(Eq.5)
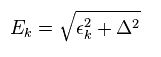
Of course, the definions of Eq.2 and Eq.3 are artificial things.
There are NO reason why the form of interacting energy becomes like Eq.2.
These are only for getting some values close to experimental ones.
In Eq.5, Δ is "energy gap", and εk is
(Eq.6)
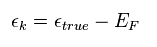
εk means the difference between true energy and Fermi energy (= EF ).
So when this εk is zero, it is equal to Fermi energy.
(Fig.12) Fermi energy is very vague concept.
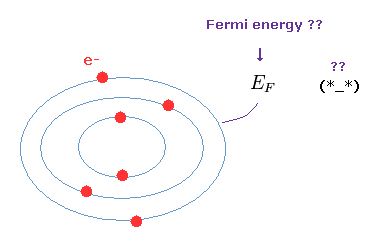
Condensed matter physics often uses the concept of Fermi energy (= EF ).
As shown on this page, the current quantum mechanics cannot express concrete electron's states.
They can only show mathematics such as matrices.
So they need to depend on some roughly approximate models.
Orbitals become occupied in order from the lowest energy levels.
Each orbit contains two electrons due to Pauli exclusion principle.
The highest energy level of outer orbital is called "Fermi level ( energy )".
So these electrons in Fermi level cannot enter inner orbitals, which are already filled with other electrons.
Unfortunately there are NO clear images in these concepts. Very abstract and useless.
(Eq.7)
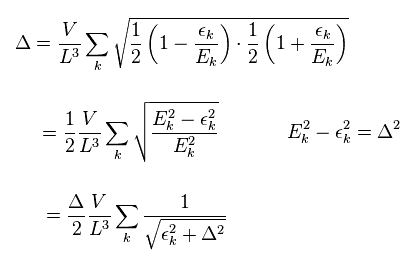
Substituting Eq.4 into Eq.2, we get Eq.7. ( Eq.5 is used. )
Dividing both sides of Eq.7 by Δ, we get
(Eq.8)
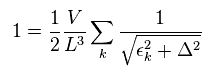
Here we change discrete wave number "k" (= momentum, energy ) into continuum,
(Eq.9)
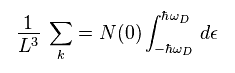
In Eq.9, N(0) means electron density, and ħω is the maximum energy of quasiparticles.
Using Eq.9, Eq.8 becomes
(Eq.10)
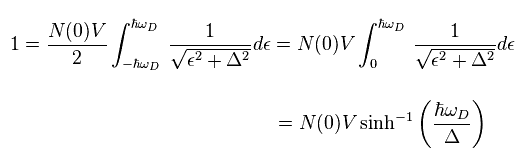
Here we use the formula of
(Eq.11)
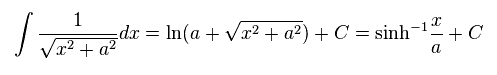
where
(Eq.12)
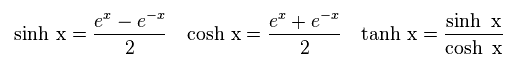
Supposing N(0)V is very small, e-x of Eq.12 becomes zero, so we get
(Eq.13)
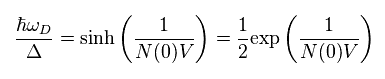
where
(Eq.14)
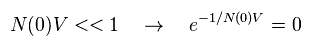
As a result, we obtain the first important relation,
(Eq.15)
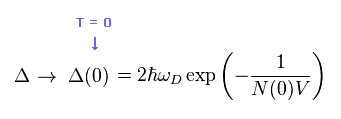
As I said, the relation of Eq.15 is that at absolute zero ( Δ = Δ(0) ).
And the artificial definitions of Eq.2 and Eq.3 lead to the final result of Eq.15.
(Eq.16)
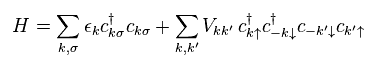
They define BCS Hamiltonian like Eq.16.
" ↑ ↓ " mean spin direction of each electron.
Total momentum of a pair of two electrons is supposed to be zero.
So when one electron's momentum is "k", another is "-k", they insist.
"V" means transition (= interactive ) potential energy between momentums k and k' in Cooper pair.
Surprisingly, these are NO positive nuclei in this potential energy. (= Only electrons. )
But they insist, these negative electrons can attract each other. This is strange.
(Eq.17)
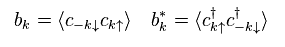
Here we define operator "b" like Eq.17.
"†" denotes a complex conjugate.
(Eq.18)
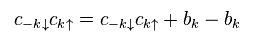
Using Eq.17 and Eq.18 in Eq.16, we get Hamiltonian of
(Eq.19)
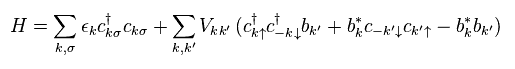
In the process of getting Eq.19, they use some trick.
They can arbitrarily choose " c c† " or " b b* " as operators.
(Eq.19') Trick ↓ Which do we choose " c c† " or " b b* " ??
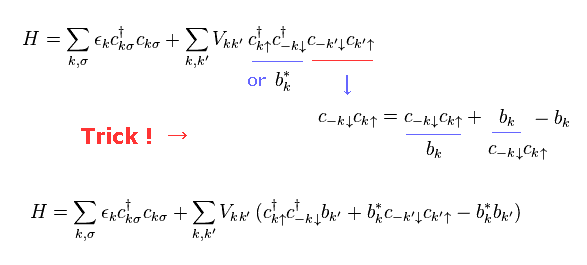
Here we define energy gap Δ like
(Eq.20)
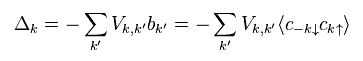
Strange to say, this energy consists only of annihilation and annihilation operators (= c c ).
This means the gap energy always becomes zero ? If so, BCS prediction is wrong.
Using Eq.20 in Eq.19, we get
(Eq.21)
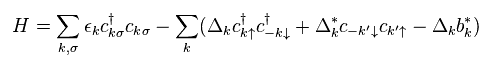
As I said in Trick-2 and Eq.19', the last term (= Δkb* ) of Eq.21 also consists of "c†" operators.
But they artificially ignore only this last term.
This is one of important tricks in BCS theory.
(Eq.22) c = electron, γ = quasifermion ?
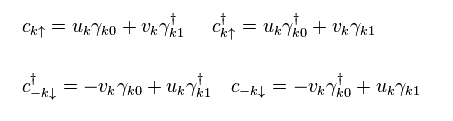
In Eq.22, γk0 and γk1 denote virtual quasifermions "1" and "2", respectively.
We can also express the relation of Eq.22 like
(Eq.23)
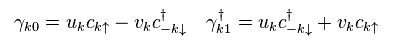
If you substitute Eq.23 into Eq.22, you can find Eq.22 and Eq.23 are the same relations.
Here we suppose electrons (= "c" ) satisfy anticommutative relation,
(Eq.24)
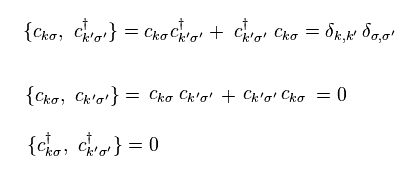
If Eq.24 holds, quasiparticles of γ also satisfy
(Eq.25)
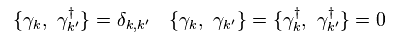
So they insist virtual quasiparticle γ is also "fermion".
But this quasifermion is just virtual and unreal, because
(Eq.26) Annihilation of quasifermion from vacuum → NOT zero !?
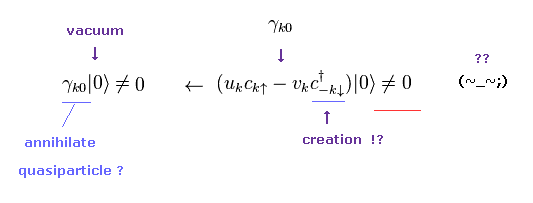
As shown in Eq.26, even when we apply some annihilation operator of quasiparticle to the vacuum, this vacuum is NOT zero.
( Because γ contains creation operator of c†, too. )
So this phonon is completely different from ordinary fermions such as electrons.
This is the reason why they are called "quasiparticles".
Substituting Eq.22 into "c" and "c†" in the first term of Eq.21, we get
(Eq.27)
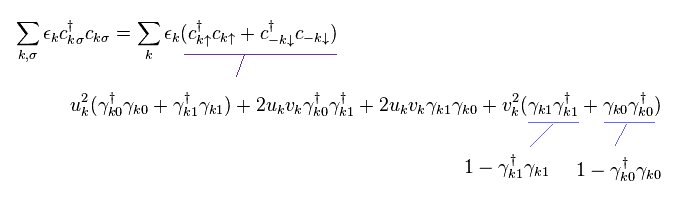
In the same way, substituting Eq.22 into "c" and "c†" in the remaining terms ( except for the last term "b" ! ← trick ) , and summing all terms, Hamiltonian of Eq,21 becomes
(Eq.28)
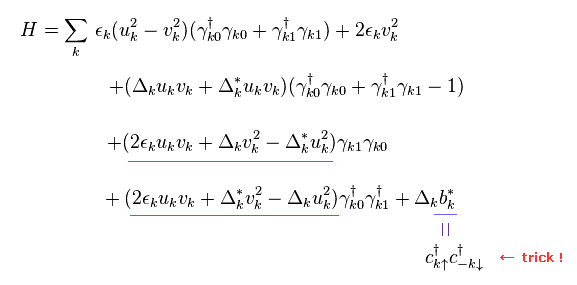
As I said in Trick-2, "c†" operators are still left only inside the last term "b*".
But they don't try to replace only these "c†" inside the last b* with γ using Eq.22.
This is clearly unreasonable calculation and trick.
They suppose Eq.29 is satisfied in Eq.28.
(Eq.29)
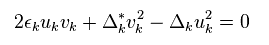
Furthermore, they artificially define
(Eq.30)
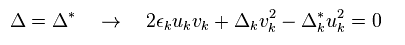
Unfortunately, the definition of Eq.30 is completely wrong.
Because Δ is NOT equal to Δ*.
(Eq.31)
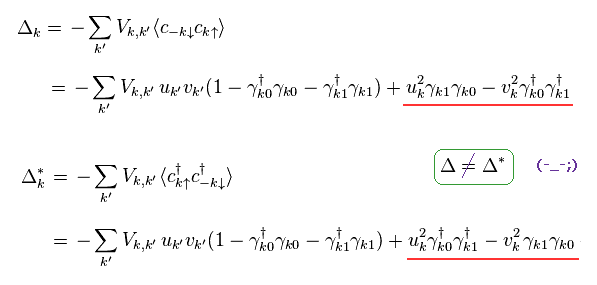
Surprisingly, they try to ignore the last two terms (= red line ) !
This is the most important trick (= Trick-1 ).
Even if you try to look for some reasonable reason in some websites and textbooks, you wouldn't find it.
Because, Eq.30 is completely wrong. ( see also appendix )
Using the definition of ( see appendix )
(Eq.32)
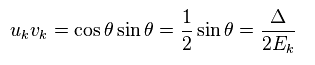
and
(Eq.3)
(Eq.4)
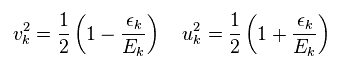
(Eq.5)
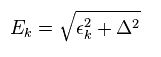
Hamiltonian of Eq.28 becomes ( using Eq.29 and Eq.30 )
(Eq.33)
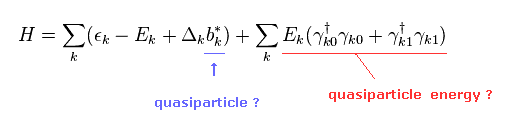
So they insist the red line of Eq.33 means quasifermion's energy (= E ) and number operators.
And the remaining term is treated as "unneeded" constant.
But as you see in Eq.17, this "b*" term still contains "c†" operators !
As a result, by using the replacement of Eq.22, you will find this "b*" term becomes another quasifermion's energy, which changes the BCS results.
But they intentionally ignore only this term.
This is one of important tricks (= Trick 2 ), and shows the current BCS theory is wrong.
Energy gap Δ can be expressed as ( see Eq.20 )
(Eq.34)

Substituting Eq.22 into Eq.34, we have
(Eq.35)
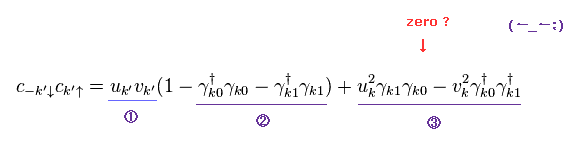
Suprisingly, they suddenly and secretly erase only the last two terms (= "3" ) in Eq.35 !
(This important fact is hidden from most textbooks and websites. )
This manipulation is very unreasonable, of course, a mistake in calculation.
There is NO reason why we can erase only "3" terms in Eq.35.
( see also appendix )
And we insert the following Fermi's distribution into number operator (= γ† γ ),
(Eq.36)
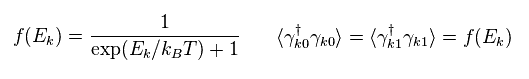
As a result,
(Eq.37)
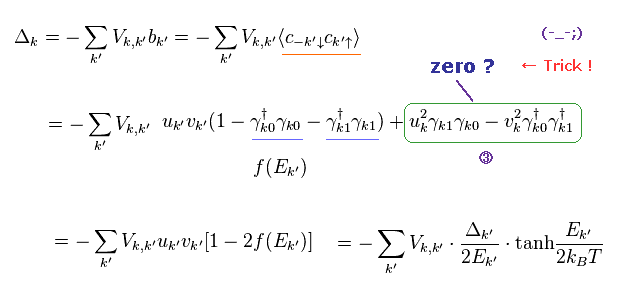
where
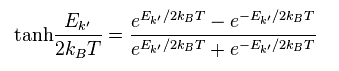
Of course, this virtual fermion doesn't really exist. ( See Eq.26 )
So there is NO reality in BCS theory.
And we have to leave only terms except "3" for getting proper results.
First, this Δ itself consists only of annihilation operators (= "cc" ), as shown in the first equation of Eq.37.
So this energy is NOT conserved and vanishes into zero from the beginning. This is strange.
And it is very artificial trick (= Trick 1 ) to delete only "3" terms.
(Eq.38)
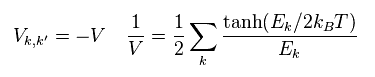
They determine interactive potential V as some constant (= -V ).
( So BCS theory is a very rough approximation. )
Inserting -V into Eq.37, and dividing both sides by Δ, we get Eq.38.
Here we change discrete momentum into continuum (= integral ) like
(Eq.39)
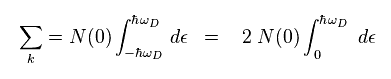
Using Eq.39 in Eq.38, we have
(Eq.40)
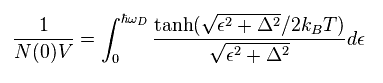
where
(Eq.41)
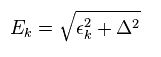
Eq.40 is the direct result of BCS theory.
The important point is that the original Eq.40 does NOT show the relation of
(Eq.42)
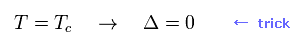
To be close to experimental result, energy gap Δ needs to be zero at the critical temperature (= Tc ).
They have to artificially apply new relation of Eq.42 in Eq.40, so partially integrating it,
(Eq.43)

In Eq.43, they treat ħω as infinity only in "1" and integral parts.
As a result, we get approximate result of Eq.43 at critical temperature (= Tc, Δ = 0 ).
As shown in Eq.40, the original result does NOT say anything about Δ value at Tc
(Eq.44)
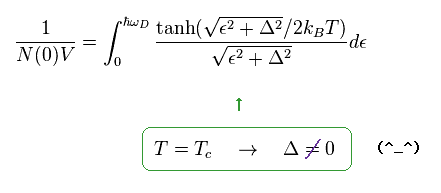
So, Eq.43 is NOT a natural result.
Ee.43 becomes
(Eq.45)
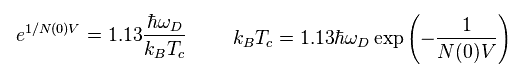
Here we use the result at absolute zero of Eq.15
(Eq.15)
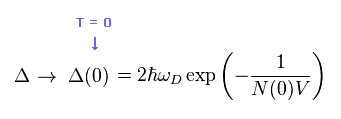
From Eq.45 and Eq.15, we have
(Eq.46) Prediction.
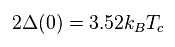
Eq.46 is the famous BCS prediction between energy gap ( Δ at T=0 ) and the critical temperature (= Tc ).
But as I said in Fig.10, there are many materials that do NOT obey Eq.46.
And to get Eq.46, they need to make intentional mistakes in calculation (= Trick 1, 2 ).
So the result of Eq.46 is unreasonable.
Here we use Boltzmann constant β and add two terms in right side of Eq.40
(Eq.47)
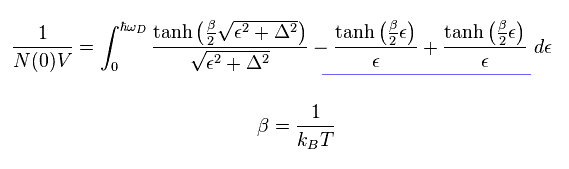
Here we use approximation of Eq.43 in left side and only the last term of right side.
(Eq.48)
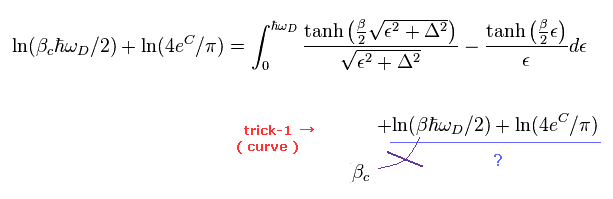
The important point is that the temperature "T" inside β in the last term of Eq.47 ( Eq.48 ) is NOT critical temperature.
But they use the approximation (of critical temperature ) also in this last term.
This is also one of tricks to get the result in which Δ becomes zero at the critical temperature.
Eq.48 becomes
(Eq.49)
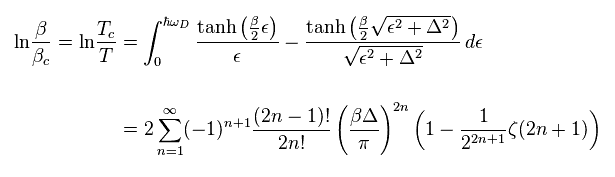
Again we use another approximation of
(Eq.50)
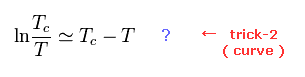
In Eq.49, we pick up only ( n=1 ) term, supposing Δ is very small.
Using also Eq.50, Eq.49 becomes
(Eq.51)

Dividing Eq.51 by Eq.46, we have
(Eq.52)
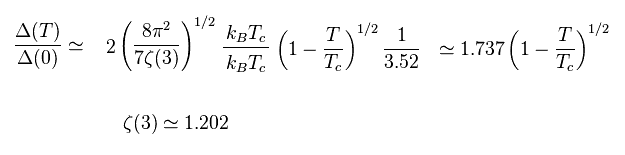
So, they insist BCS theory can predict curve like Fig.13.
But as you see several approximations of Eq.48, Eq.50 and Eq.51, they just intentionally try to obtain Fig.13 curve.

The direct (= original ) BCS calculating results do NOT show the curve of Fig.13 at all.
(Eq.53)
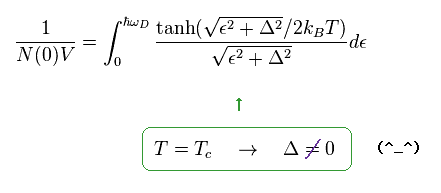
The critical magnetic field is the experimental value, we can most exactly measure.
According to these results, the relation between specific heat (= Cs ) and the critical temperature (= Tc ) becomes
(Eq.54)
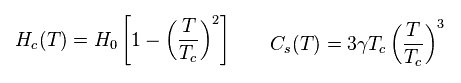
Eq.54 is different from BCS prediction (= exponential ) of
(Eq.55)
The ratio of specific heat is gotten from the BCS theory of Eq.37.
But as I said, these calculations are just mistakes, which means BCS theory cannot predict anything.
(Fig.14) The relation of specific heat doesn't satisfy BCS theory.

Actually this relation of Fig.14 is violated in various superconductors.
(Fig.15) Detecting infinitesimal tunnel current ?
In fact, it is very difficult to detect energy gap Δ in superconductors.
They apply some voltage (= energy Δ ) or light to superconductor, exciting "phonons".
This excited phonons are detected as small tunnel currents, they insist.
( Though they call it "tunnel", each particle cannot penetrate barriers more than "nanometers", so it just indicates some de Broglie wave's effects. )
But of course, there is some detection threshold in amplifier and detector of this current.
If we change the setting of this amplifier, the critical voltage changes, too.
So this is very similar to a single photon (= "fiction" ) detection.
(Fig.16) It is impossible to make tunnel current completely zero.
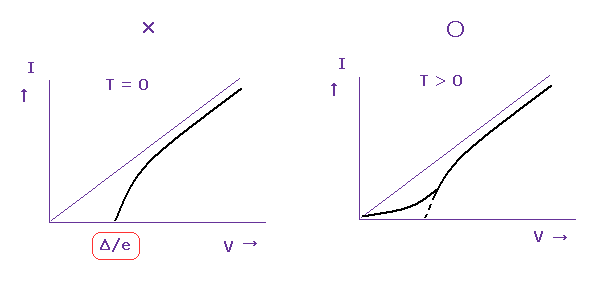
Theoretically, the energy of phonon (= ε ) becomes completly zero at absolute zero ( T = 0 K, Fig.16 left ).
But it is impossible to get complete absolute zero temperature.
So small tunnel currents are always detected, even when NO voltage is applied (= Fig.16 right ).
This is also a cause of some errors.
Using the definitions of Aq.1 and Aq.2,
(Ap.1)
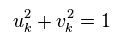
(Ap.2)
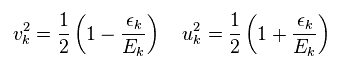
we get
(Ap.3)
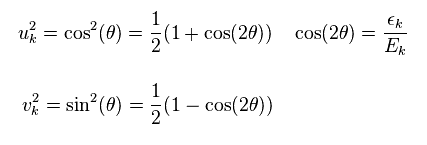
As a result, we obtain the result of Eq.32.
(Ap.4)
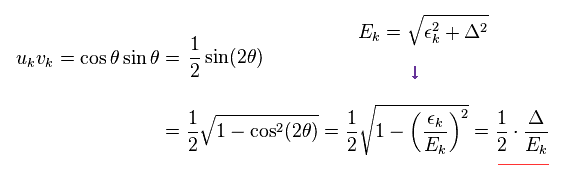
We defined "quasifermion" like Eq.23 (= Ap.5 ),
(Ap.5)
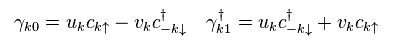
Using Ap.5, we prove this quasifermion is completely different from real particles.
Because even if annihilation operator (= γ ) is applied to the vacuum (= |0> ), this vacuum does NOT become zero, as shown in Ap.6.

So they define new unrealistic quasiparticle's vacuum like
(Ap.7) Quasiparticle (= BCS ) vacuum ??
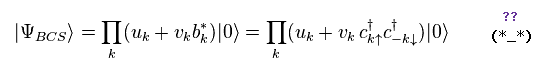
Using Ap.5 and Ap.7, we can prove
(Ap.8)
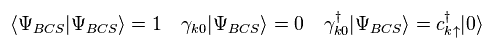
where we use
(Ap.9)
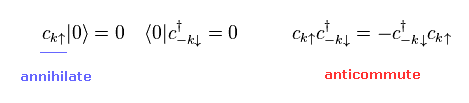
So we can say Ap.7 is quasiparticle's vacuum.
Of course, this vacuum is not real, because electron's annihilation operator (= c ) cannot make this vacuum zero.
(Ap.10)
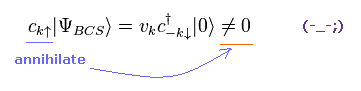
By the way, what happen when the following "b" operators are put between this quasiparticle's vacuum ?
(Ap.11)
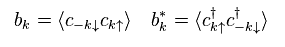
Using Ap.7, Ap11 and anticommutative relation, we get
(Ap.12)
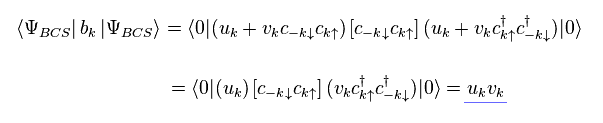
In the same way,
(Ap.13)
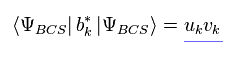
This is the reason why they insist Δ = Δ* in Eq.30, as follows,
(Ap.14)
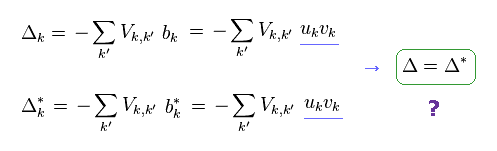
But in fact, if Ap.14 is satisfied, we cannot get the BCS predictions of Fig.10 and Fig.11.
(Ap.15)
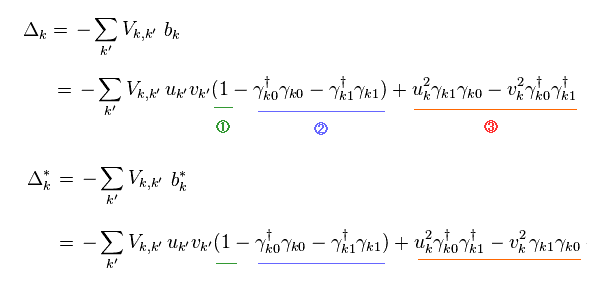
They try to delete only "3" terms in Ap.15, and leave "1" and "2" terms.
This is one of important tricks in BCS theory.
As you notice, this artificial choice is unreasonable and completely wrong in both usual and quasiparticle's vacuums.
If BCS vacuum contains one quasifermion, only "2" term is left ( "1" and "3" vanish ).
And if BCS vacuum contains two quasifermions, only "3" term is left.
So the assumption that "1" and "2" terms are left has NO ground at all.

2013/12/12 updated. Feel free to link to this site.