Home page
Einstein is false
relativistic force paradox
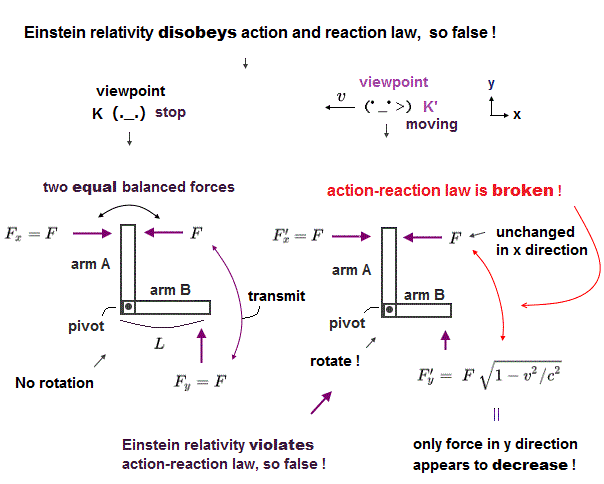
(Fig.1) Equal forces F acting on a stationary right-angle lever seen by K is changed as seen by a moving K' who paradoxically sees the lever rotated.

In Fig.1, two equal forces F in x and y directions act on the right-angle lever, which keep the right-angle lever stationary as seen by a stationary observer K.
But as seen by an observer K' moving at a velocity v in -x direction, only the force in y direction Fy weakens ( this-last, this p.14-15, this p.35 = force Fx in x direction remains the same seen by K and K' unlike Fy ), and resultantly, the whole right-angle lever appears to be rotated only when seen by K' due to the unequal, unbalanced forces in x and y directions.
↑ This is clearly paradox disproving Einstein relativity, because whether the lever is rotated (seen by K' ) or not rotated (seen by K ) paradoxically depends on who sees the lever.
All alleged solutions to this (true) relativistic right-angle lever use unreal ad-hoc concepts such as illusory hidden momentum P in -y direction (= called unphysical Laue current, this-8th-last-paragraph ) generated by the force F in x-direction (= directions are inconsistent ) and illusory angular momentum caused by a unreal string connecting K' observer and the lever.
(Fig.2) As seen by the moving K', one arm of the lever is Lorentz-length contracted, and force in y direction weakens, which paradoxically rotates the lever.
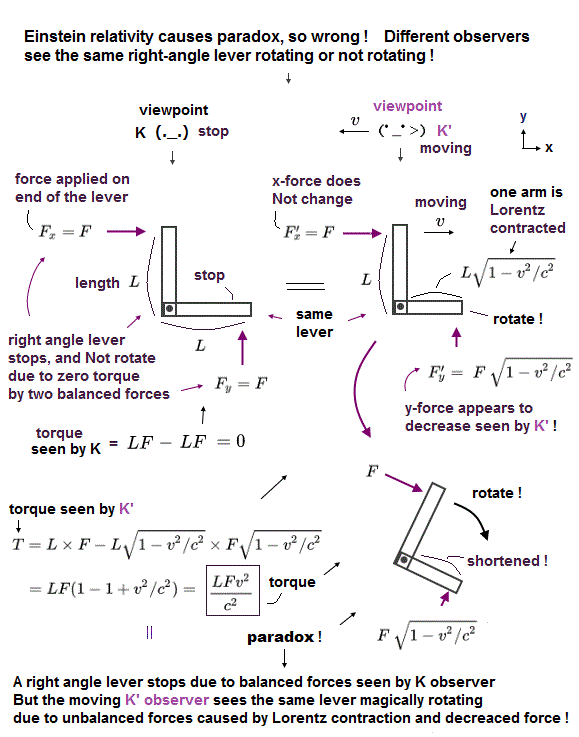
A stationary right-angle lever on which two equal forces F act paradoxically appears to be rotated only when seen by a moving K'.
Because one arm in x-direction is Lorentz length contracted.
And only the force F in y-direction appears to weaken as seen by the moving K' by Lorentz factor ( while force F in x-direction remains the same as seen by K and K' )
As a result, the torque T rotating the whole right-angle lever (= sum of length × force ) is Not zero (= LFv2/c2 ) only when seen by the moving K', which is a real relativistic paradox with No consistent solutions.
(Fig.3) Force F in x direction paradoxically injects an illusory hidden momentum P in -y direction, which could cancel the rotation of lever, combined with the illusory angular momentum caused by a non-existent string ?
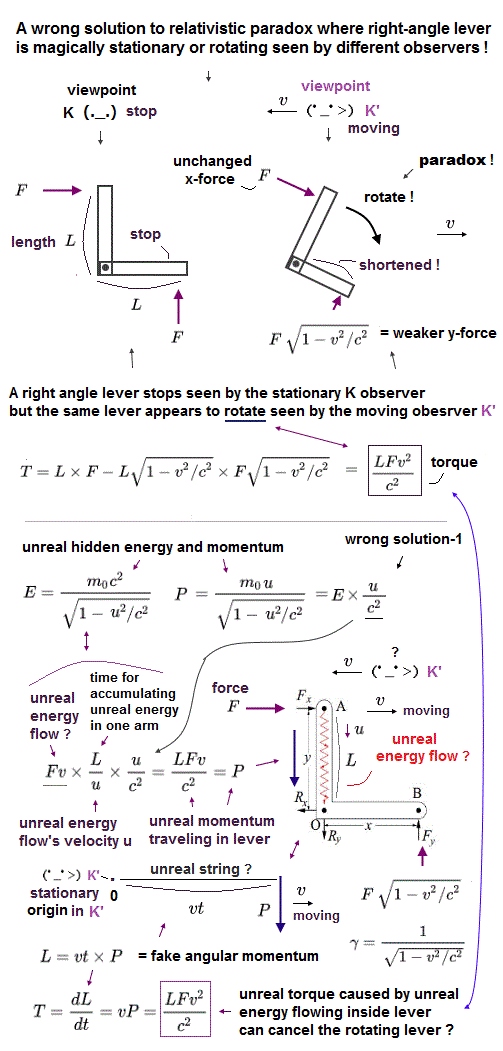
All solutions to this relativistic right-angle lever paradox are illegitimate, based on unrealistic ad-hoc concepts.
They unreasonably claim that the force F acting on the lever in x direction (paradoxically) generates the hidden momentum P (= called Laue current ) in -y direction (= which is wrong, because directions of the applied F in x direction and the resultant momentum P in -y direction are inconsistent, this p.3-Figure.1 and p.3-last-paragraph ).
↑ Even if this illusory momentum (Laue) current is real, this current (= caused by force F in x direction ) hitting the wall of the lever generates momentums of both ±y directions, which cannot generate the above hidden momentum P in -y direction (= so this cannot solve the right-angle lever paradox ).
Furthermore, these solutions rely on an illusory string connecting a moving observer K' and the lever, allegedly causing (illusory) hidden angular momentum L (= hidden momentum P × vt v is velocity of K' and t is time ) and an unreal torque T ( = time derivative of L ) just canceling the torque rotating the lever ( this p.3-4, this p.1-right, p.2-right ).
↑ But these centers of rotation are different between the torque rotating the lever around pivot and the illusory torque whose center of rotation is said to be the moving observer K' linked by the unreal string, so these two different torques with different centers (= based on the unreal string ) cannot cancel each other, and No solution to this paradox.
As a result, these solutions and ad-hoc torques are unable to solve the rotated right-angle lever paradox.
The 8th-last-paragraph of this site says
"In his efforts to explain the paradox, [Laue] invented the concept of the momentum of the "elastic energy current". Laue made the ad hoc assumption that an elastic energy current exists from one end of the lever arm perpendicular to v to the other end of that same lever arm"
This p.2-1st-paragraph says
"The published and
unpublished discussions have introduced a wide variety of explanations, generally introducing ad hoc effects of questionable validity to keep the moving lever. ← No legitimate solutions to this right-angle lever paradox
from rotating."
Another solution tries to use two different relativistic accelerations of two lever arms (= unreasonably omitting relativistic mass ) instead of force, which is wrong ( this p.3-(9)-(12) ), because the forces (= Not acceleration ) determine whether the lever is rotated or not (= all parts of the rigid right-angle lever must be rotated together under only one common acceleration, so this solution based on two different accelerations of two different parts of one lever is wrong ).
Another solution falsely assumes the rigid right-angle lever seen by K' can deform and change the right-angle (= against the fact of the rigid lever ) due to paradoxical Lorentz length contraction.
↑ But also when seen by the moving K' (= the whole lever is moving in x direction ), the rigid body remains rigid, so it is impossible to change the right-angle by deforming the rigid lever (= changing the right angle of 90o into other angles of the rigid lever is impossible also when the lever is moving, due to violating energy conservation law ), so this solution is also illegitimate.

Feel free to link to this site.