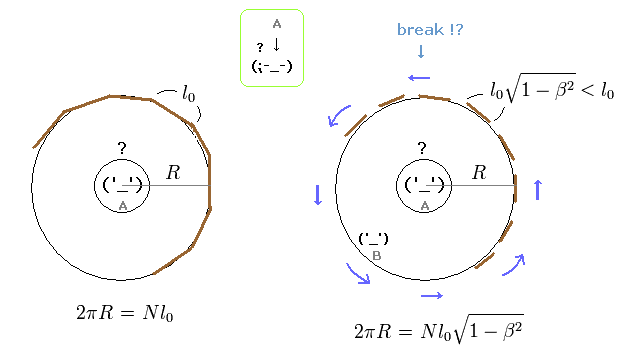
Home page
Einstein is wrong (2/5/2025)
Ehrenfest paradox is real.
(Fig.1) Which is a "true" circumference of rotating disc ?
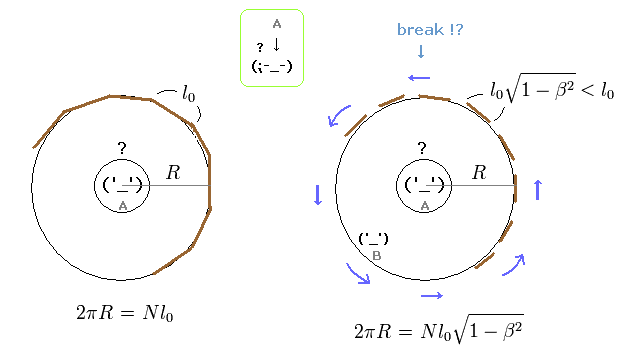
In the left panel of Fig.1, a disc-like object with a hole in its center is at rest.
The observer A is at rest in the central hole.
And only the observer B is on the disc.
The radius of this disc is R.
N × short stick with the length of " l0 " are aligned along the periphery.
This means the circumference of this disc at rest is 2πR = Nl0.
In the right panel of Fig.1, the disc is spinning at the angular frequency ω.
So each stick is Lorentz contracted from the viewpoint of the observer A, as shown in Fig.1 right.
The radius R is perpendicular to the moving direction of each stick, so the radius R is NOT contracted.
The observer A at rest is in ordinary Euclidean geometric space, so the circumference from the observer A always becomes 2πR.
But due to the Lorentz contraction of each stick, this 2πR is NOT equal to Nl0, when the disc is rotating.
This is completely a paradox in the special relativity (= Ehrenfest paradox ).
This paradox originates in the weak point of the special relativity which does NOT consider more than one directions ( x and y, or rotation ) from the beginning.
From the viewpoint of the observer B moving with the rotating disc ( right panel of Fig.1 ), the length of each stick is " l0 ", because the rotating observer B is in the rest frame with respect to the rotating stick.
The observer B is in non-Euclidean space (= rotating system ), so the circumference is a little longer than 2πR.
This means a circle is "distorted" and becomes a little longer in non-Euclidean space.
This interpretation is based on the standard general relativity.
( Of course, this is a story when you believe in the general (special) relativity. )
To solve the "different circumferences" paradox, the rigid rotating disk needs to be "broken" to contract the radius R.
Of course, if this rigid disc is not broken, this paradox leads to the fact that special relativity includes self-contradiction.
(Fig.2) Observer's "looking" power rotates the electric wire !
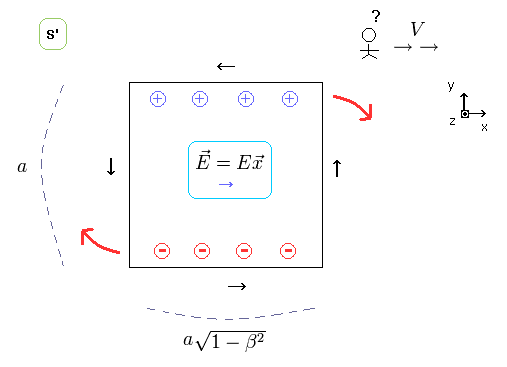
As shown in this page, the neutral current generates strange charges to satisfy Lorentz law by the simple observer's movement.
Special relativity can explain ONLY the direction in which Lorentz force equation is valid ( F = eE + ev×B ).
But it does NOT consider the rotating direction (= torque caused by the generated charges ) from the beginning.
This is clearly a important weak point of the special relativity.
(Fig.3) Observer's looking power moves the charged particle !

In Fig.3, near the neutral current wire loop, one minus charge and one plus charge are at rest in S frame.
But from the S' frame, these charges are attracted to the current wires, which generate strange charges, as shown in Fig.3, right.
( See also this page. )
This direction shows weak point of the special relativity.
Because, the magnetic force, which act on the charge can NOT be parallel to the charge's moving direction.
This means the special relativity can NOT deal with two directions.
(Fig.4) Right-angle lever paradox.
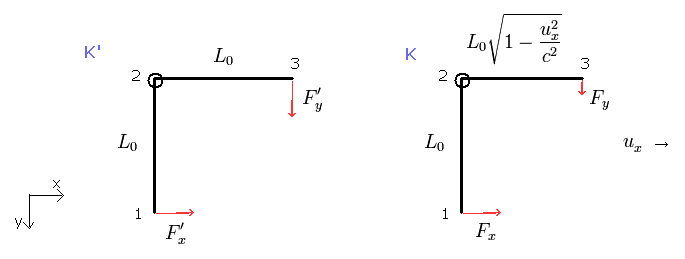
As shown in this page, Fig.4 shows the right-angle lever at rest is rotated ONLY by the simple observer's movement who doesn't touch the lever at all.
This is completely a paradox of the special relativity, too.
As a result, special relativity can NOT control more than one directions correctly.
( Special relativity does NOT have the power to deal with more than one directions. )
This is the "essence" of the relativistic problem and shows the special (general) relativity is wrong.
The ordinary textbooks of the relativity should deal with these "real" paradoxes, rather than "fake" paradoxes, I think.
( But unfortunately, these important paradoxes are NOT seen in the ordinary textbooks at all. Why ?? )

2012/6/20 updated. Feel free to link to this site.