トップページ (2電子原子も含む正確な新ボーア模型)
奇妙なスピンは 実在しない。
スピンホール効果は "スピン" を意味しない。
様々な値の計算。
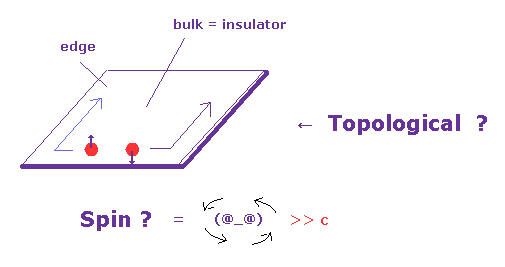
(Fig.1) トポロジカル絶縁体?

トポロジカル絶縁体は Hg(Cd)Te などの特殊な複合体で、その物質の内部 (= バルク ) の大部分は 絶縁体なのに、周辺部 ( 2次元系では 端、エッジ部分 ) のみ 導電性を示す ( ウィキ、 このサイト (p.17) 参照のこと )。
現在の理論によれば、2次元系のトポロジカル絶縁体では、 "アップ" と "ダウン" の スピンを持つ電子が 周辺部分に沿って 互いに逆方向へ動いていることになっている ( つまり 混合しているため 各スピンは観測できない )。
実際、非現実的な スピン 自体は 直接観測することができない。
後で説明するが、このトポロジカル絶縁体の 直接的な実験結果は スピンでなく、単に 電気伝導性 に基づいている。
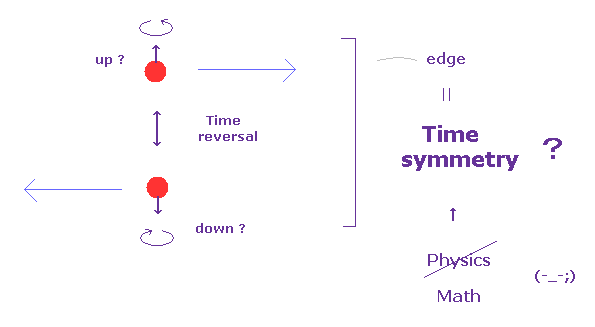
(Fig.2) "時間反転対称性" が トポロジカル絶縁体の 主要な要因? ← これが物理?
ところで、一体何が このトポロジカル絶縁体を引き起こす要因になっているのだろうか?
現在の標準的な量子力学によれば、この主要な メカニズム は "時間反転対称性" によるとされている。
Fig.2 では、 "アップ" スピンの電子が 右方向へ動いている。
もし 時間の進む向きを逆にできたとしたら、 回転向きが反転するため、スピンの向きが逆になる。
さらに、電子の進行方向も逆になる ( 右方向 → 左方向 )。
Fig.1 で述べたように、トポロジカル絶縁体は 両方のスピン状態を含んでいることになっている。
つまり 時間反転対称性は この両方向性の状態を 壊すことにならない。
だからこれが原因だと言うわけである。
しかし お気づきのとおり、現在の理論では 状態そのものを述べたにすぎず、具体的なメカニズムに関しては 何も 語ろうとしていない。
困ったことに、現在の物理は 非常に抽象的な数式記号と遊んでいるだけで、具体的な物理的原因の解明から逃げているのである。
(Fig.3) "質量ゼロ" のディラック電子は 実在するのか? それとも仮想粒子?
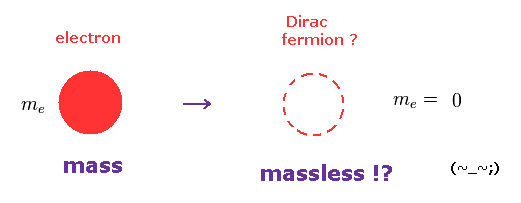
驚くことに、現在の物理学者達は トポロジカル絶縁体や グラフェンにおいて 質量ゼロの ディラック粒子が 実在すると 主張しているのである。 このサイト や このサイト参照のこと。
もちろん、質量ゼロのディラック電子 (= フェルミ粒子 ) は 完全に 架空の粒子であることは言うまでもない。
彼らは 角度分解光電子分光 ( APRES ) というものを用い、物質に 光を照射して 飛び出てきた電子のエネルギーと運動量を測定することによって、この関係式から "質量ゼロ"と推定しているにすぎない。
ご存じのとおり、各電子には "質量" が ある ことは言うまでもない。
つまり 質量のある電子の測定を基にした 質量ゼロのディラック電子 という結論は 明らかに 自己矛盾以外何者でもない。
驚くことに、このサイトにあるように、 トップジャーナルでさえ、非現実的な 質量ゼロのディラック電子があると 堂々と公言しているのである。
後で説明するが、ARPES を用いた実験は奇妙な仮定に基づいており、かつ実験結果自体も 非常に 曖昧なものしかでない ( 例えば ディラックコーンを参照のこと )。
(Fig.4) 磁気モノポールは 実在するのか ?
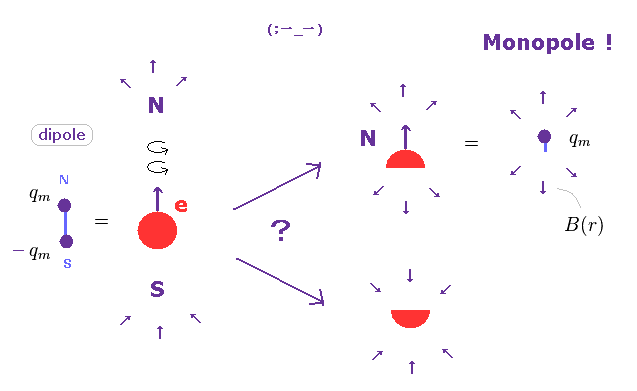
磁気単極子 ( モノポール ) は N 極 もしくは S 極 の 片方だけを分離してできた 仮想の物質である。 ウィキ参照のこと。
もちろん、この磁気モノポールは 単なる フィクションのため、まったく 実験的証拠がない。
なぜなら 磁場というのは 電荷の運動によって生じるもので、磁荷なるものは 実在しないからである。
(Fig.5) 磁気モノポールは 存在するのか? 単なる "数式の" トリック ?
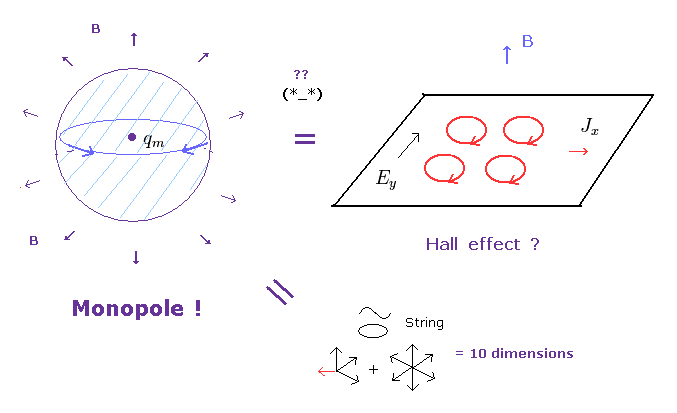
現在まで モノポールの実験的な証拠は まったくないにも関わらず、 現在の物理学者達は このモノポールを 現実の 量子ホール効果 ( や 10次元の超弦理論 ) に用いようとしているのである。 このサイト. このサイト (p.3 右) 参照のこと。
なぜなら 現在の量子力学は リアルな物理の世界を避けて、架空の 数式の技巧 や 準粒子 のみに走る傾向があるからである。
後で モノポールそのものが 数学 かつ 物理学の両方の視点からして
あり得ないことを証明する。
単なる 数学上のトリックに走るだけでは 本当のサイエンスの発展は 永久に ないのは明らかである。
(Fig.6) ベリー位相は 仮想の ( リアルでない ) 位相。 ← 物理 ?
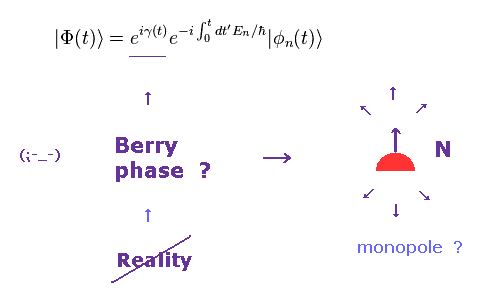
ベリー位相 ( このサイト、 このサイト、 このサイト 参照のこと ) は ( 異常 ) 量子ホール効果などの物理現象を説明するために 意図的に導入された 所謂 仮想の位相である。
現在の物理学には このような抽象的で はっきりとした形のない 概念に頼りすぎているところがある。
後で説明するが、このベリー位相は 物理学的にも数学的にも 非常に 人為的な定義に基づいており、物理現象の根本的な解明には 何も役に立っていない。
つまり 量子ホール効果などの 真のメカニズムは 今なお 謎のまま ということになる。
(Fig.7) 磁束量子 (= Φ ) の いくつかの渦が 各電子に張り付いている?
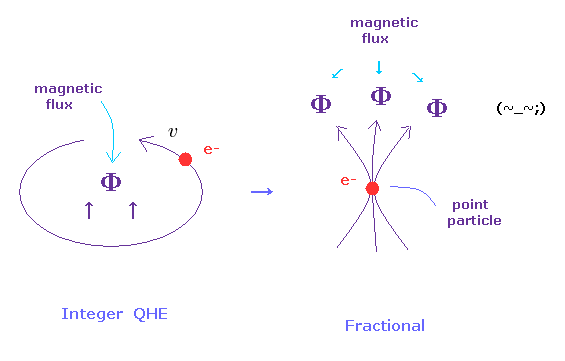
量子ホール効果では、各電子は 外電場に 垂直な 方向に動いている。
そのため 磁気ローレンツ力 (= ev× B ) が 電気力 (= eE ) と ちょうど 釣り合っていることになる。
分数量子ホール効果 (= FQHE ) では、ホール伝導度は e2/h の分数倍になっている。 ウィキ参照のこと。
通常、磁束 (= Φ ) は 磁束密度 (= B ) × 面積 (= S ) で表されるため、 Φ = BS となる。
しかし、分数量子ホール効果では、何と 点状粒子である電子が Fig.7 右に示したように、内部に いくつもの磁束量子を 抱え込んでいることになっている。 ここ、 ここ、 ここ も参照のこと。
現実的な観点からして、点状粒子の狭い範囲に いくつもの磁束量子を含むことは あり得ないことである。
(Fig.8) エニオン = 分数電荷は 実在するのか ?
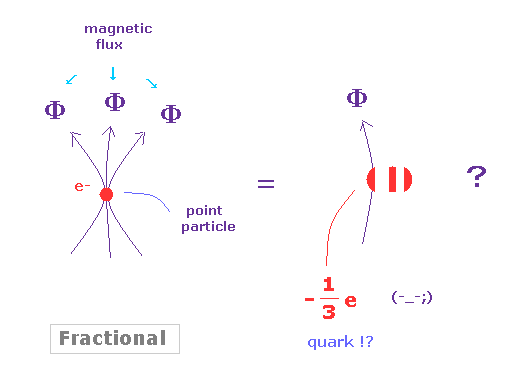
驚くことに、 このサイト、 このサイト、 このサイト にあるように、現在の物理は 1/3e, 1/2e .. などの 分数電荷 ( クォークでなく ) が実際に存在するとしているのである。
と言っても、もちろん 分数電荷は 完全に 架空の概念であることは言うまでもない。
つまり これらは 実際の粒子でない準粒子の1つである。
問題は 現在の 量子力学は この準粒子の詳しい実像を それ以上 問おうとしないことである。
(Fig.9) 磁気モノポールは実在しない。
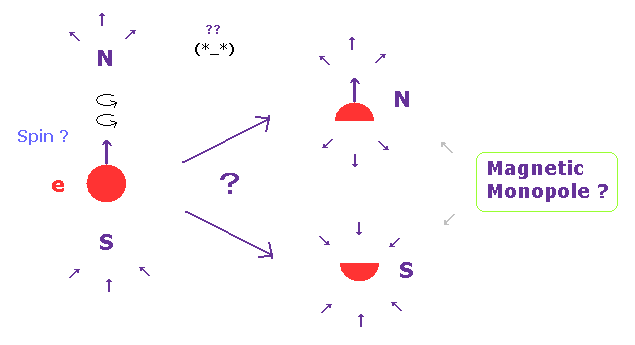
磁気モノポールは 実在しない仮想の粒子である。
磁荷は N もしくは S 極のみからなる。
問題なのは "現実離れ"が好きな量子力学や宇宙論が この 幻のモノポールを (スピン)量子ホール効果、 ジャーナル、 初期宇宙 などに利用しようとしている点である。
(Fig.10) 磁束密度 (= B )、磁束 (= Φ ), ベクトルポテンシャル (= A ).
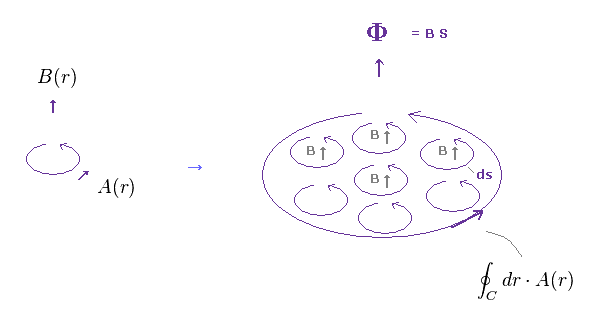
単位面積当たりの 磁束密度 (= 磁場 ) は ベクトルポテンシャル A を用いて表せる。 ここ、 ここ、 ここ など参照のこと。
(Eq.1) B = A の回転
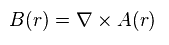
磁束 (= Φ ) は B 磁場の 面積分 (= S ) で与えられる。
結果、全磁束は ベクトルポテンシャル A の その周囲の線積分 (= C ) と等しくなる。
( このサイト参照のこと )。
(Eq.2)
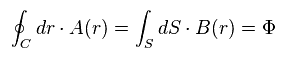
(Fig.11) 磁気双極子と単極子。双極子のみ実在する。
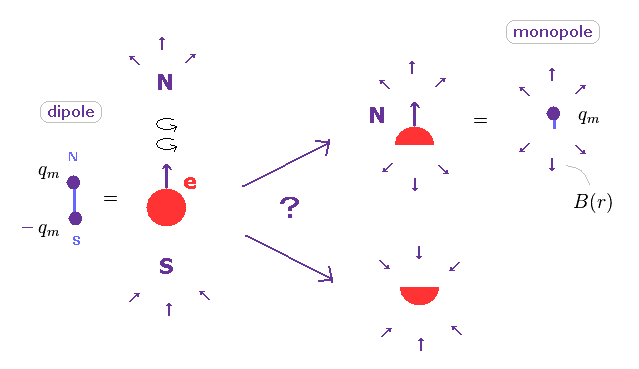
もし 磁気モノポールが実在したとしたら、磁場 B は Eq.3 にあるように磁荷 (= qm ) を用いて表せる。
(Eq.3) 磁気モノポール qm
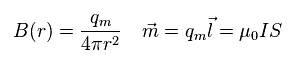
Eq.3 では、磁荷 × l ( = ± qm 間の距離 ) が 磁気双極子 (= m ) ということになる。
この磁気双極子は 電流 I × 面積 (= S ) と等しく、もちろんこれは現実に存在する。
(Eq.4) モノポール周囲の ベクトルポテンシャル "A" 。
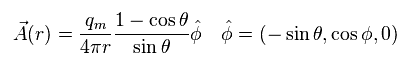
このサイト (p.9) や このサイト にあるように、モノポール周囲の ベクトルポテンシャル A は Eq.4 のようになる。
(Fig.12) 球面上の 1部分 (= S ) に含まれる 磁束
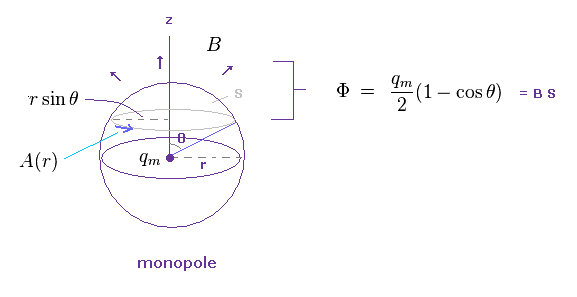
上部の球面上 ( 0 < 角度 < θ ) を通過する 磁束 (= Φ ) の全量は Fig.12 のようになる。
この部分における A (= Eq.4 ) の線積分 と B (= Eq.3 ) の面積分 は 次のように 同じ結果を与える。
(Eq.5) ベクトルポテンシャル "A" と 磁場 "B" との関係。
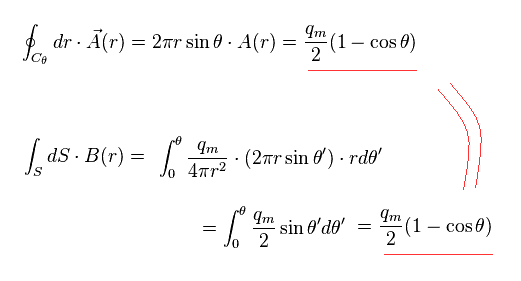
よって Eq.4 の形が正しいことが分かる。
(Fig.13) 磁場 B は θ = π で 無限大に発散してしまう。
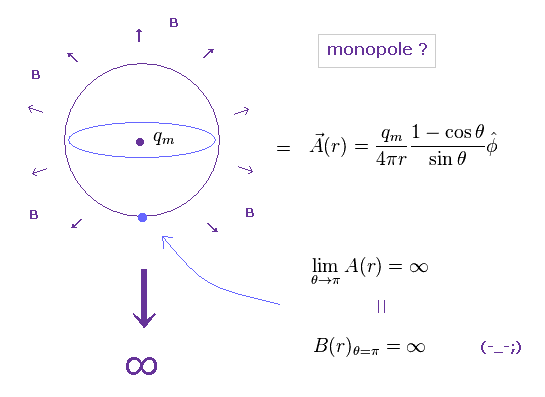
しかし この形には 1つ 重大な問題が存在する。
Fig.13 のように、ある1点 ( この場合、 θ = π ) で ベクトルポテンシャル A ( と 磁場 B ) は 必ず 無限大に発散してしまう。
つまり Eq.4 は モノポールによって生じるとされる 磁場 (= Eq.3 ) と矛盾してしまう。
この事実は 空想上の磁気モノポールが 数学的にも 実在し得ない重要な理由の1つである。
(Fig.14) 上半分の球面からでる 全磁束 (= Φ )。
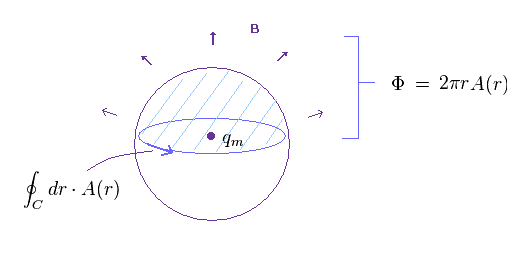
Fig.14 に示したように、 Eq.2 を用いると、上半分の球面からでる 全磁束は 2πr A になる。
(Fig.15) 下半分の球面からである 全磁束 (= Φ )。
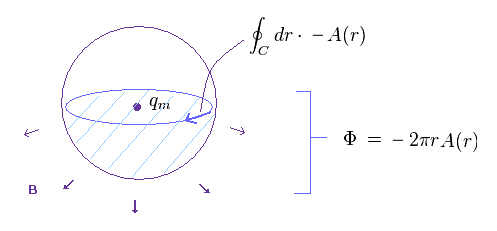
一方で、下半球からの視点では Fig.15 に示したように 赤道線上で ベクトルポテンシャル A の符号が 逆になる。
つまり 下半球面に含まれる 全磁束は Fig.14 のと ちょうど逆になる。
(Eq.6) 磁気モノポールは 必ず ゼロになる !?

磁気モノポール ( 磁荷 qm ) は 全球面からでる 全磁束に等しい。
しかし Fig.14 (= 上球面 ) と Fig.15 (= 下球面 ) の合計は 打ち消し合って Eq.6 のように 必ず ゼロになってしまう。
これが "A の回転"の 重要な性質である。
( 回転 に基づくということは、磁気双極子のみが実在し、単極子は 実在しないということである。 )
(Fig.16) モノポール (= 磁荷 ) は 必ずゼロになる。
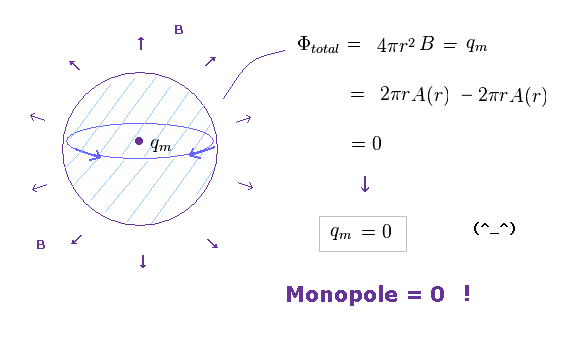
要するに、磁場が ベクトルポテンシャルの "回転" で表される限り ( B = ∇ × A )、磁荷は 必ず キャンセルされて ゼロになってしまうことになる。
非常に 矛盾した怪しい存在である。
実は、Fig.13 において 無限大を 無視したために、 この不一致が 生じたのである。
もちろん、 無限大に発散する特異点が あるという時点で モノポールは 現実の物ではない。
(Fig.17) 赤道線上で向きを変えると・・ AN → AS !?
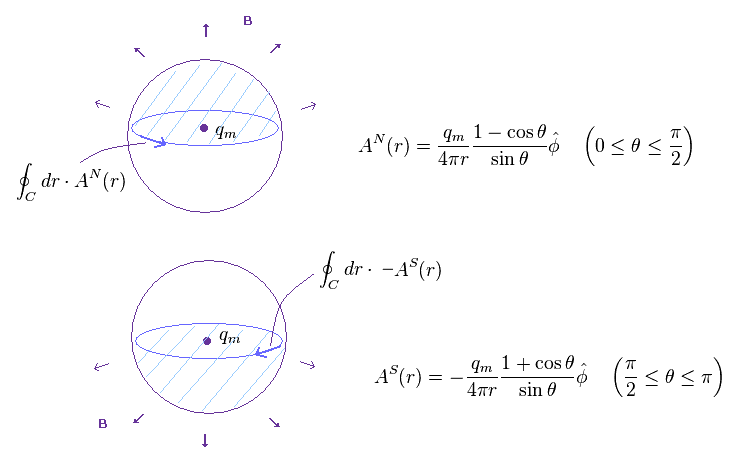
Fig.16 における矛盾を避けるために、 Fig.17 のような 非常に人為的なルールに頼る必要がある。
Fig.17 では、ベクトルポテンシャル "A" が 上半球と 下半球の境界線上で 突然 ガラリと 変わってしまっている ( AN → AS )。
この変化は 物理的にも 数学的にも 不連続であるため、 モノポール自体 無理やりこしらえた存在であることが分かる ( Fig.18 下図 )。
(Eq.7) 磁気モノポール ?
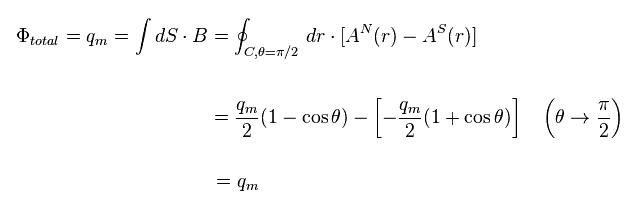
Fig.17 の 非常に人為的な ルールを用いると、 Eq.7 に示したような ゼロでない磁荷 (= qm ) が得られる ( このサイト や このサイト (p.9) も参照のこと )。
(Fig.18) モノポールは 非常に非現実的である。
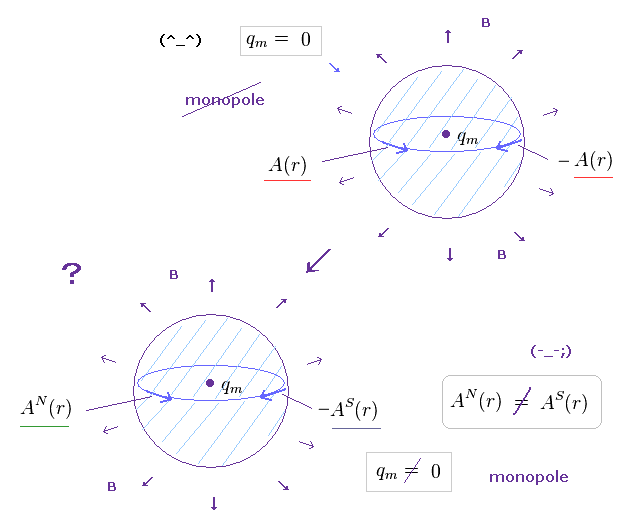
問題なのは、物理学者達は この磁気モノポールを 他の現実の物理現象と結びつけようとしている点である。
その中の重要なものに 量子ホール効果 (= QHE ) がある。
(Fig.19) ( スピン ) 量子ホール効果 = モノポール !?
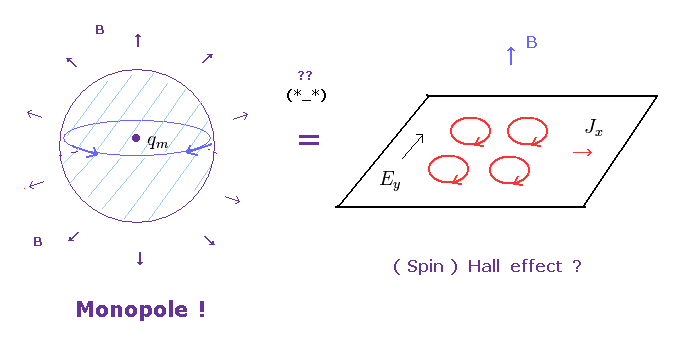
あなた方も思われたように、この結びつけは 現実的な見地からして 決して 受け入れ難いものである。
つまり、量子ホール効果に対する現在の解釈は まったく正確とは 言えない。
(Fig.20) ベリー位相とは何か ? = "非実在の" モノポールの応用 ?

ベリー位相は 非常に抽象的な概念で、しばしば 量子ホール効果に現れる。
Fig.20 に示したように、 彼らは 意図的に 元の固有関数に 他の数学上の 位相 (= γ(t) ) をつけた。
元の固有関数では、時間発展を表す指数関数は ハミルトニアン (= エネルギー E ) である。
しかし それがベリー位相を含むと、この単純な関係式が 成り立たないということになる。
この位相は 基礎的な場の量子論の時間発展の考えに 明らかに 矛盾するものである。
(Eq.8) ベリー位相 ?
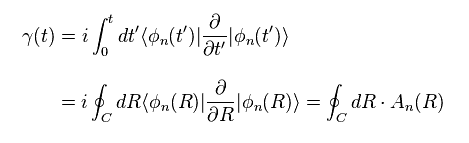
固有関数 φ が 何らかのパラメーター "R" ( この R は 任意の概念である ) に依存していると仮定する。
時間が "0" から "t" に変わる間に、この系が 元の状態に戻るとする (= 断熱的な循環 )。
(Eq.9) 磁気モノポール ?
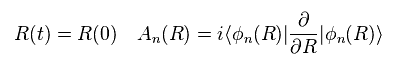
任意のパラメーター R にそった線積分は ベクトルポテンシャル A と 磁場 B の関係に似ている
( B = ∇ × A )。
そのため 彼らは Eq.9 で 新たな 人工的な ベクトルポテンシャルを定義した。
このベリー位相における ベクトルポテンシャル "A" を "ベリー接続" と呼ぶ。
(Eq.9') ベリー曲率。
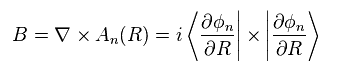
さらに、この "A" の回転は 磁場 (= B ) に似ており、これを "ベリー曲率" と呼ぶ。
Eq.8 の詳細な計算は このページを参照のこと。
(Fig.21) 2次元電子系。.
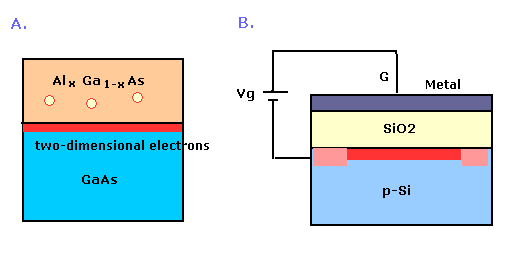
量子ホール効果は 低温、高磁場下における 2次元電子系で、ホール伝導度が量子化された値 (= n e2/h ) になる現象である。
ここ, ここ、 ここ など参照のこと。
この系では、動いている電子は Fig.21 の赤い部分で示した 1平面上に閉じ込められていることになる。
この状態にするには、半導体と他の物質で挟んだ構造にする。
このサイト参照のこと。
(Fig.22) 2次元電子系。
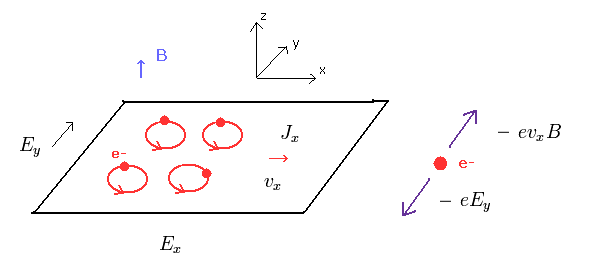
強磁場 (= B ) のもとでは、各電子は 円形なサイクロトロン運動をしている。
遠心力が 磁気ローレンツ力 (= ev× B ) と釣り合っている。
このエネルギー準位は 量子化されている (= ランダウ準位量子化 ).
(Fig.23)
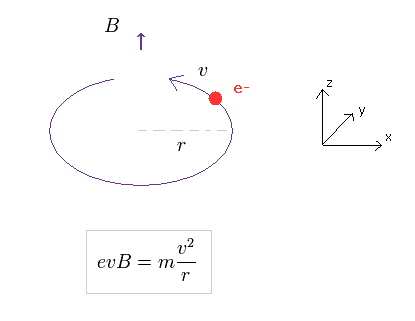
結果的に この円運動の角振動数 (= ω ) は
(Eq.10)
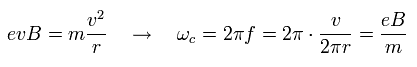
ここで y 方向に 外電場 (= Ey ) をかけると、この電気力 (= -eEy ) が 磁気力 (= -evx × B ) に等しくなる。
つまり 各円軌道は x方向へ動くことになる。
そして この時の ホール伝導度 (= σxy ) は 量子化されることになる。
(Eq.11)
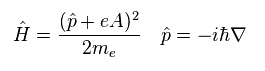
このページにあるように、外磁場のもとでは ハミルトニアンは Eq.11 に変化する。
"A" は ベクトル ( 磁気 ) ポテンシャルである。
(Eq.12)
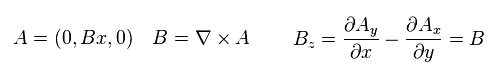
ベクトルポテンシャル A の各成分を Eq.12 と仮定する。
この条件では、磁場 B が z 方向を向く。
Eq.12 の "A" を Eq.11 に代入して、
(Eq.13)
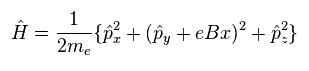
Eq.13 のハミルトニアンでは、 y、 z 成分は 自由電子である。
つまり 波動関数を次のように定義できる。
(Eq.14)
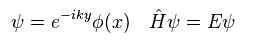
運動量が -iħ∇、 かつ Eq.14 を用いると、 ハミルトニアン (= エネルギー ) は Eq.15 ( x-y 平面上で ) になる。
(Eq.15)
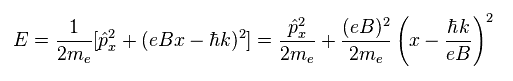
Eq.16 の調和振動子のハミルトニアンを解くと、 このサイトにあるように 量子化されたエネルギー準位が得られる。
( もちろん、量子化は ドブロイ波長に関係する。 )
(Eq.16)
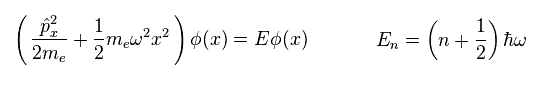
ここでは
(Eq.17)
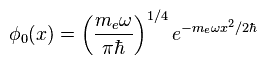
Eq.15 を Eq.16 と比較して、角振動数 ω は、
(Eq.18)
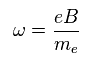
Eq.18 は 古典力学 (= Eq.10 ) の結果と同じである。
(Eq.19) "波" が y 方向に量子化されている。
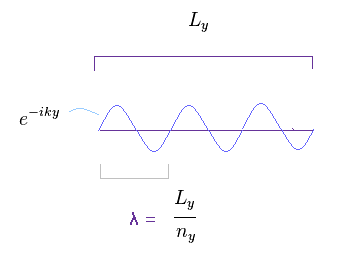
重要な点は 電子の密度 (= Ns ) が 量子化されることによって、 これが ホール伝導度 ( もしくは 抵抗 ) の量子化として現れるということである。
この電子2次元系の面積を Lx × Ly と仮定する。
ドブロイ波の整数倍が 各方向に適用されているとすると、この波長 λ は y 方向に Ly/n となる ( "n" は整数 )。
(Eq.20)
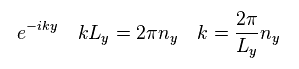
波数 "k" は 2π/λ。
ご覧のとおり、現在の量子力学は 明らかに 量子化されたドブロイ波に依存しているが、この事実を 決して認めようとしない。非常に奇妙である。
Eq.19 から、 Eq.20 を得る。
(Eq.21)
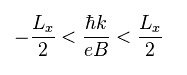
Eq.15 から、この調和振動子の 中心点は ħk/eB である。
x 方向の1辺が Lx とすると、 Eq.21 を得る。
(Eq.22)
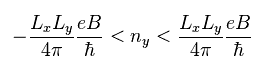
Eq.20 の波数 k ( y 方向 ) を Eq.21 に代入して、 Eq.22 を得る。
つまり 状態密度 (= Ns このサイト p.8 も参照 ) は、
(Eq.23)
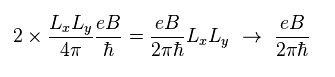
ここで その面積 LxLy で割っている。
Eq.23 を次のように表せる。
(Eq.24)
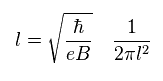
Eq.24 の結果は このサイト p.9、 このサイト p.18-p.20 などにも等しい。
このように 量子力学は 非常に抽象的な概念である 波数 "k" 空間に依存している。
このことが もっと複雑な現実的な系に 理論を素直に発展できない妨げになっている。
(Eq.25)
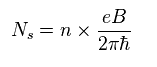
さらに、"n" のランダウ準位の電子密度 (= Ns ) を Eq.25 のように定義する。 .
もちろん、これは 単なる 人為的な定義にすぎない。
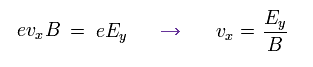
Fig.22 から、 y 方向の速度が Eq.26 になる。
Eq.25 と Eq.26 を用いると、電流密度 (= jy ) は
(Eq.27)
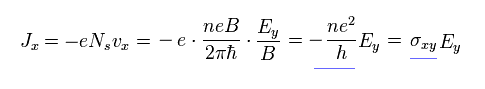
ここでは ħ = h/2π。
結果的に ホール伝導度 (= σxy ) は Eq.28 になる。
( ホール伝導度とは y 方向の外電場と x 方向の電流の比のことである。 )
(Eq.28)
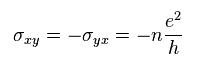
これが 整数量子ホール効果の伝導度である。
( ホール抵抗 ρ は ホール伝導度の逆数である。 ρ = 1/σ )
(Fig.24) 複数の磁束 (= Φ ) が 電子に張り付いている ?
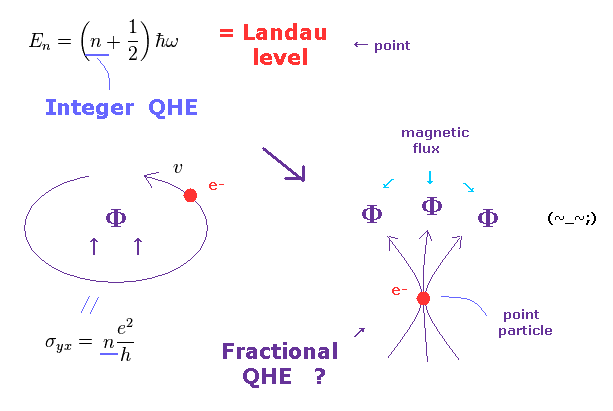
整数量子ホール効果 (= IQHE ) が まず最初に発見されて、Eq.16 のランダウ準位の 整数 (= n ) をそれに割り当てた。
ここまでは言いとして 問題は 後に 分数量子ホール効果 (= FQHE ) が 発見されてしまったことである。
このことが深刻な問題を引き起こした。
なぜなら ランダウ準位の概念を 整数量子ホール効果で すでに使い切ってしまったため、それを今さら修正して利用するということができないからである。
つまり 分数量子ホール効果を説明するための 道具が もう残っていないのである。
この厳しい状況で、物理学者達は 複数の磁束 (= Φ ) が 点状粒子である電子に張り付いているという 非常に奇妙な アイデアに頼るしか道がなかったのである。 Fig.24 右図、 このサイト, このサイト, このサイト (Fig.6) 参照のこと。
(Fig.25) エニオン = 分数電荷は 実在するのか?

これはつまり 分数電荷をもつ 奇妙な準粒子が 分数量子ホール効果において 出現していることになってしまう。 このサイト、 このサイト、 このサイト 参照のこと。
Eq.25 の、2次元系での 電子密度を 次のように表せる。
(Eq.29) 量子化された電子密度。
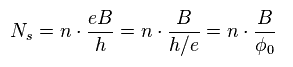
"n" が整数のとき、これは 整数量子ホール効果になる。
Eq.29 では、 "h/e" は 磁束量子である。
注意: 量子ホール効果では 磁束 (= φ0 ) は 元々の 磁束量子 の2倍の奇妙な値を基本にしている。
これは 人為的なルールである。
(Eq.30) 分数量子ホール効果
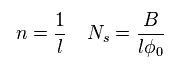
Eq.29 が正しいとすると、分数量子ホール効果で "n" は 分数 (= 1/l ) になれる。
これはつまり、各電子の電荷 (= e ) は Eq.31 に示したように 分数電荷 (= 1/l e ) になれることになる。
(Eq.31)
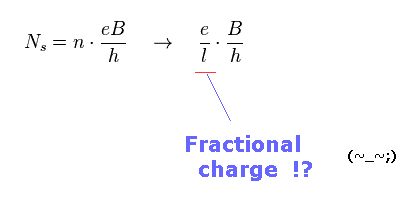
もちろん、この分数電荷というのは フィクション以外何者でもない。
単なる 準粒子という定義上のものだが、問題は 現在の量子力学は こういった曖昧な概念を 野放しにして ( むしろ 新しく増やそうとしている )、かつ 決してこの準粒子が 何かと問おうとしないことである。
理論的な計算に関しては このページを参照のこと。
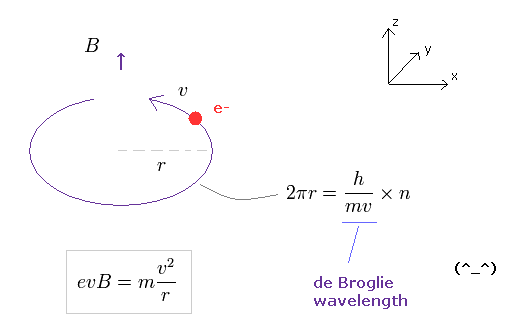
(Fig.26) 整数倍のドブロイ波長。
お気づきのとおり、分数量子ホール効果になって 突然 分数電荷やら、複数の磁束が 電子にくっついているだとか まったく異なる概念を使い始めるのは 不自然極まりない。
このセクションでは、共通のドブロイ波の概念を用いて、整数、分数の両方のホール効果を自然に説明できることを示す。
Fig.26 では、各電子は 外磁場 B のもとで、円形に運動している。
境界条件 (= ドブロイ波の端同士が 互いにフィット ) を考慮すると、軌道長 (= 2π r ) は ドブロイ波長の整数倍となる。
(Eq.32)
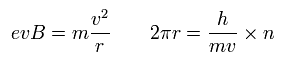
最初の式は 遠心力が ローレンツ力に等しいことを表している。
二番目の式は n × ドブロイ波長 ( λ = h/mv ) である。
実は 量子力学においても 境界条件として ドブロイ波長の整数倍に頼っているのである。例えば このサイト。
Eq.32 を解くと、
(Eq.33)
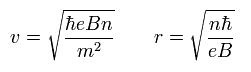
ここでは ħ = h/2π である。
Eq.33 から、円の面積は
(Eq.34)
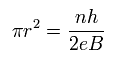
Eq.32 から、角振動数 ω は
(Eq.35)
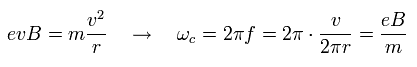
この ω は 量子力学のランダウ準位 (= Eq.16, Eq.18 ) に等しい。
ここで Eq.34 の面積内に k 個の電子が含まれているとする。
(Fig.27) 2次元電子系
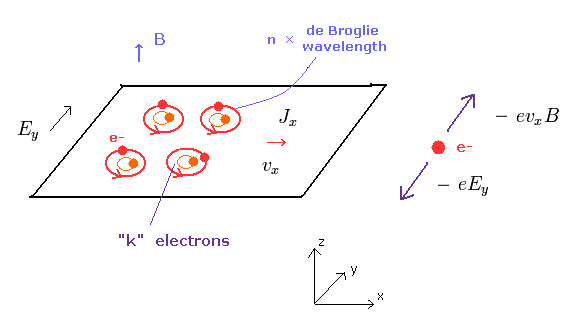
Fig.27 に示したように、速度 vx は、
(Eq.36)
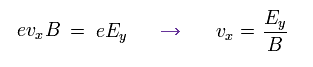
Eq.34 と Eq.36 を用いて、電場 Ey による x 方向の 電流密度 (Jx) は、
(Eq.37)
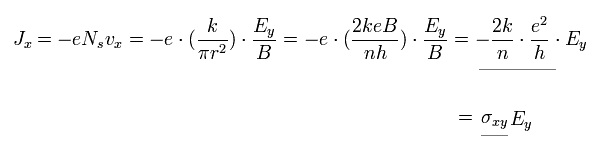
Eq.37 から、ホール伝導度 σxy は
(Eq.38)
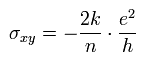
Eq.38 は 整数、分数両方のホール効果を説明できる。
Eq.38 の分母の 因子 "2" のために、その既約分数の分母の数は 奇数になりやすい。
ホール抵抗 ρxy は ホール伝導率の逆数で表される。
(Eq.39)
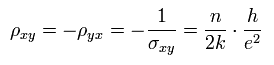
基本的に、対角抵抗 (= ρxx ) が ゼロになるとき、 ホール抵抗は プラトーになり、ホール伝導率 σxy ( もしくは ホール抵抗 ρxy ) は Fig.28 にあるように 分数値も含めて 量子化されることになる。
(Fig.28) 実験結果。
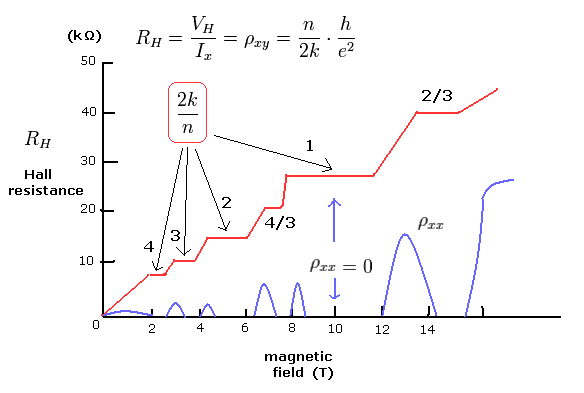
Eq.37、Eq.38 の具体的な状態を考えてみる。
"n" は 軌道1周に含まれる ドブロイ波長の数であり、 k は この軌道円に含まれる 電子の数である。
最初に 2k/n = 1 の場合を考える ( Fig.29 も参照 )。
( このケースは Eq.28 の n=1 の整数ホール効果に該当する。)
例えば、 2 × ドブロイ波長の 1軌道 (n=2) が 1つの電子を含んでいるとき ( k=1, Fig.29 )、
(Fig.29) 2k/n = 1 の一例 ← 整数
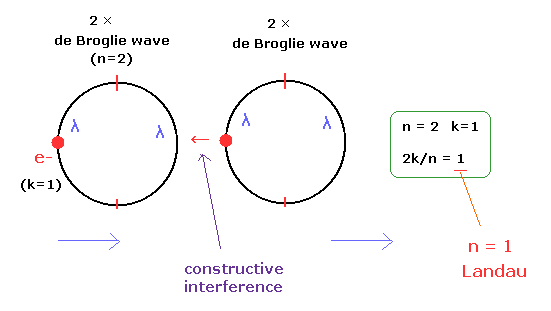
Fig.29 は Fig.28 の n = 1 のプラトーにあたる。
このケースでは 各軌道は 2 × ドブロイ波長のため、それらの波の位相は 同位相の 同調的な干渉作用を起こし安定になり得る
もちろん、2次元系と言えども この層は 有限の 厚さがあることは言うまでもない。
つまり 複数の電子層が この電流に関与し得る。
これらのケースが n = 1, 2, 3, ... × の整数量子ホール効果の一要因となり得る。
(Fig.30) 2k/n = 2/3 の一例。 ← 分数。
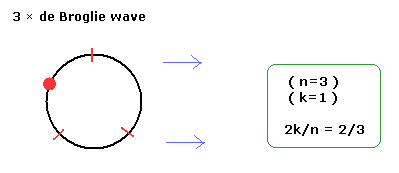
次に 2k/n = 2/3 のケースについて考える。
このケースは Eq.28 と Eq.31 の n= 2/3 のケースにあたる。つまり 分数量子ホール効果である。
例えば、 3 × ドブロイ波長の1軌道 (n=3) が 1つの電子を 含むとする。
( 結果、 k= 1).
Eq.34 に示したように、磁気力 (= B ) が強くなるにつれて、軌道半径が小さく (= 電子間の反発力が強く ) なる。
結果的に 1円内の電子数が相対的に少なくなったことによる 分数ホール効果は 高磁場 B のもとで起きる傾向にある ( Fig.28 )。
(Fig.31) 対角抵抗 = 0 → 各軌道が 互いに 滑らかに "フィット" している。
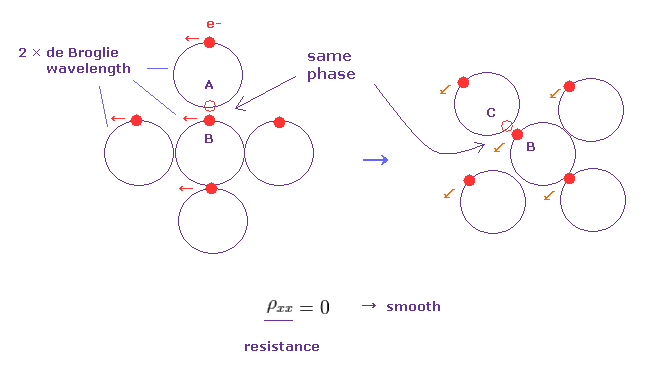
Fig.28 を見て分かるように、対角抵抗がゼロ (= ρxx = 0 ) のとき、ホール効果が見られる。
これはつまり、各電子が 互いに散乱されることなく 滑らかに動いていることを意味している。
Fig.31 を見て分かるように、 2 × ドブロイ波長の 各軌道は 同調した干渉作用で 互いに滑らかに くっついている。
電子 "B" は 回転しながら、"A" 軌道、そして "C" 軌道にくっつく。
この模型は 奇妙な分数電荷などに頼らずに、 共通の概念に基づいているため 非常に自然なものと言える。
(Fig.32) "質量ゼロ" のディラック粒子は 実在するのか?

次に トポロジカル絶縁体やグラフェンにおいて 質量ゼロのディラック電子が どうして 頻繁に登場するのか説明する。
まず結論から言うと、これらの概念は 何の物理的イメージのない数学的な概念にすぎないということである。でも頻繁に論文に登場する。困ったものである。
(Eq.40) 元の ディラック方程式。
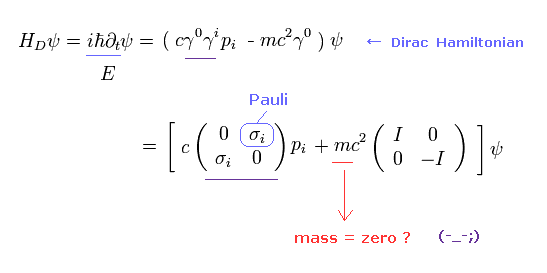
このページに示したように、ディラック方程式 ( ハミルトニアン ) は Eq.40 のようになる。
このディラック電子の質量がゼロのとき、この 4 × 4 の行列は 2 × 2 行列に分離できる。
(Eq.41) ディラックのハミルトニアン ( m = 0 )。
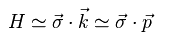
ここで パウリ行列 σ は、
(Eq.42)
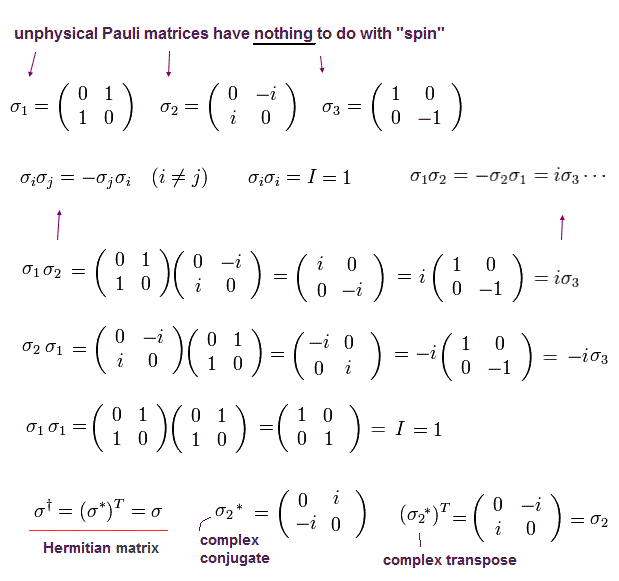
Eq.42 を用いると、 Eq.41 のハミルトニアンは
(Eq.43)
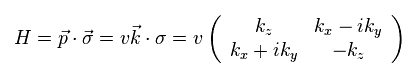
Eq.43 の固有値は 次のようになる。
(Eq.44)
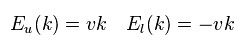
ここで 波数 "k" は、
(Eq.45)
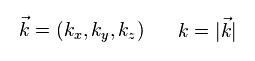
(Fig.33) "質量ゼロ" のディラック電子 ?
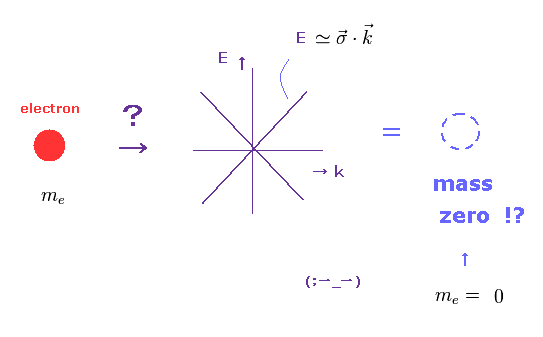
Eq.44 の 波数 k とエネルギーの関係は Fig.33 のようなグラフになる。
そのため これは 光子のエネルギー運動量のような 質量ゼロのディラック電子を意味しているという訳である。
しかし ご存じのとおり、電子が質量ゼロになってしまうことは 絶対に あるはずがない。
Eq.43 の固有関数の1つは
(Eq.46)
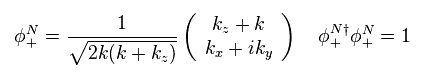
Eq.43 と Eq.46 を Eq.47 の左辺に代入して、エネルギーは 波数 "k" に 線形に比例することを確かめられる (= これが 質量ゼロ !? )
(Eq.47)
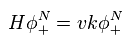
しかし Eq.46 の解には 深刻な問題がある。
kz = -k のとき、この解は 次のように 無限大に発散してしまう。
(Eq.48)
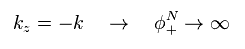
これが 質量ゼロのディラック電子が 数学的にも間違いであることの証である。
また このパターンは Fig.13 の 架空の 磁気モノポールに似ている。
(Eq.49) 同径方向の "k" = 0
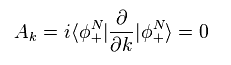
Eq.9 では、任意のパラメーター "R" が 波数 "k" のとき、ベリー接続 "A" は Eq.49 のようになる。
ここで 波数空間上の 赤道線 ( kz = 0 ) 上で、 一定の |k| の値のときの線積分を考える、
そのため Eq.49 のように 動径方向の "k" に対する偏微分は ゼロとする。
(Eq.50) 接線方向 "k"
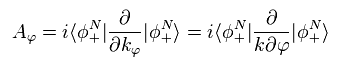
接線方向の kφ の方向のとき、ベリー接続は ゼロでないとする。
赤道上 (= k 空間の x-y 平面 ) では "kz" 成分はゼロになるため、Eq.46 の波動関数は
(Eq.51)
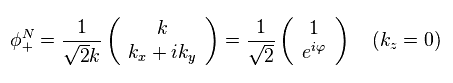
ここでは
(Eq.52)
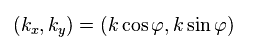
Eq.51 を Eq.50 に代入して、次を得る。
(Eq.53)
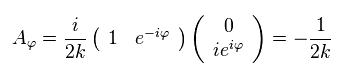
結果的に Eq.52 の線積分 (= ベリー曲率 "B" ) は
(Eq.54)
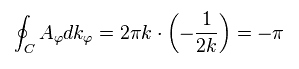
もちろん、これら "A" や "B" は "k" 空間 ( 実空間でなく ) 上における "偽"の磁気ポテンシャルである。
Eq.48 に示したように、この波動関数 φN は kz = -k の点状で 無限大に発散する。
(Eq.55)
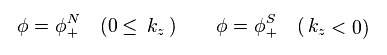
そのため 突然 Eq.55 に示したような 新たな固有関数 φS を導入することになる。
これは 非常に強引な数学である。
なぜなら 波動関数が 赤道上で 不連続に変化しているからである。
(Eq.56)
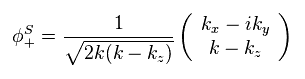
Eq.56 は 南半球用 ( kz < 0 ) の 新たな波動関数である。
見てのとおり、Eq.56 は kz = k で 無限大に発散する。
(Eq.57)
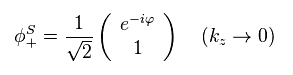
赤道上 ( kz = 0) で、この波動関数は Eq.57 のようになる。
Eq.51 と Eq.57 を比べると分かるが、これらの波動関数は kz = 0 線上で 不連続である。
(Eq.58)
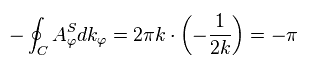
同様に、Eq.57 の線積分は -π になる。
結果的に、 磁荷 (= モノポール ) は Eq.54 と Eq.58 の合計になる。
(Eq.59)
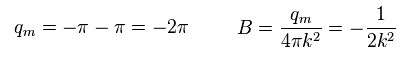
Eq.59 が 質量ゼロのディラック電子における "モノポール" である ( もちろん仮想の )。
(Fig.33)
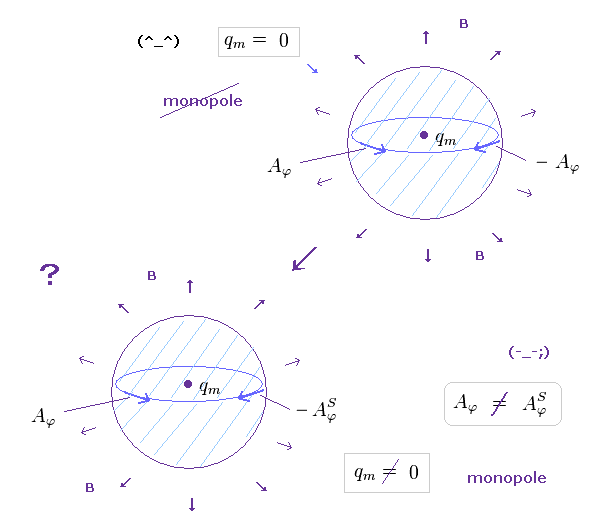
しかし この方法は 数学的にも 非常に 理不尽である。
Fig.33 下図 を見て分かるように、ベクトルポテンシャル "A" が 時計、反時計方向で 突然 変化してしまっている。
(Fig.34) ベリー位相は 単なる数式のトリック。リアリティーなし。

すでに述べたように、ベリー位相は 非常に抽象的な 数学上の概念である。
現在の量子力学は これらの位相が 一体全体何なのかという重要な質問から 逃げてばかりで 単に道具として使っているのである。
(Eq.60)
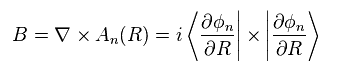
前に述べたが、ベリー曲率 (= B ) は 磁場のように、ベリー接続 (= "A" ) の回転で表される ( Eq.9'参照 )。
ハミルトニアンと固有関数は、
(Eq.61)
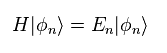
Eq.60 と Eq.61 に基づくと、次を得る。
(Eq.62)
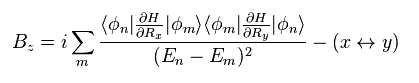
詳細な計算方法に関しては このページを参照のこと。
(Eq.63)
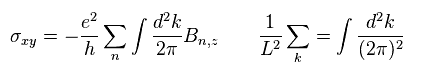
このページでは、Eq.62 のベリー曲率を用いて Eq.63 のホール伝導率を得た。
(Eq.64)
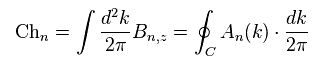
Eq.63 では、 Eq.64 の値を "チャーン数" という。
このチャーン数が 整数のとき、Eq.63 の ホール伝導率は 整数倍に量子化されることになっている。
(Fig.35) 異なったベリー接続の 意図的な定義。
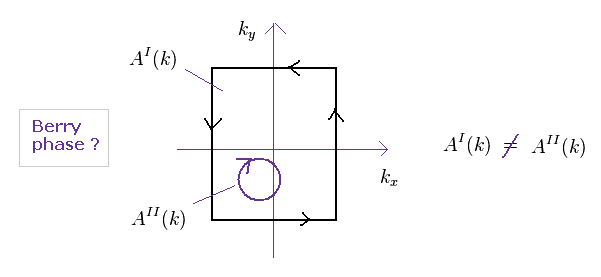
しかし 他の磁気モノポールのときのように、ブリルアンゾーンの "k" 空間すべてを含むように Eq.64 を計算すると、このチャーン数は 必ず ゼロになる。
この打ち消し効果を避けるために、再び Fig.35 のように 不連続な "A" を定義した。
Fig.35 では、ベリー位相 "A" が 突然 AII と AI の境界上で変化してしまう。
これは明らかに 現実的な根拠のない トリックの1つにすぎない。
(Eq.65)
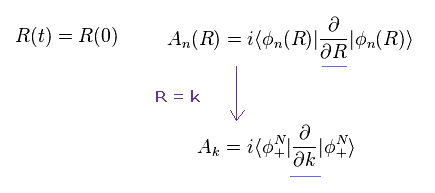
ここで Eq.9 において パラメーター R が k (= 波数 ) のときの ベリー接続を用いる。
さらに 次のような 別の ルールも人工的に定義した。
(Eq.66)
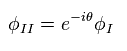
Eq.64、 Eq.65、 Eq.66 から、全チャーン数は
(Eq.67)
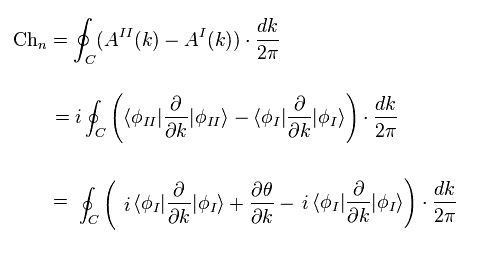
結果的に
(Eq.68)
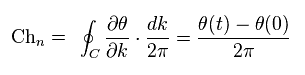
この位相が 1軌道上で 整数 (= n ) × 2π のとき、
(Eq.69)
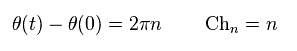
Eq.63 のホール伝導度は
(Eq.70)
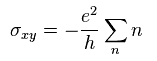
そのため ベリー位相が 整数量子ホール効果を説明できたと主張しているのである。
しかし Eq.65 をみて分かるように、このパラメーター R (= k ) は 時間 "t" の関数である。
結果的に 時間が経過するにつれて、このチャーン数は 無限大まで 増加していってしまうことになる。 ( ← 定数にはならない。 )
(Eq.71)
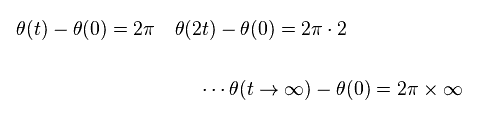
つまりこの論理によれば、 ホール伝導度 σ が 時間と伴に 無限大に増加していってしまうのだろうか? 数学的な技巧のみに走ると こういう 辻褄の合わない現象が生じることになる。
(Eq.72)
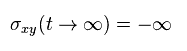
また Eq.66 の定義は 非常に人為的なものである。
なぜなら 波動関数 φII ( θ(t) を使って表わされる ) そのものが、時間 ( t, k ) とともに 変化してしまうからである。
(Fig.36) グラフェンにおける 半整数量子ホール効果。
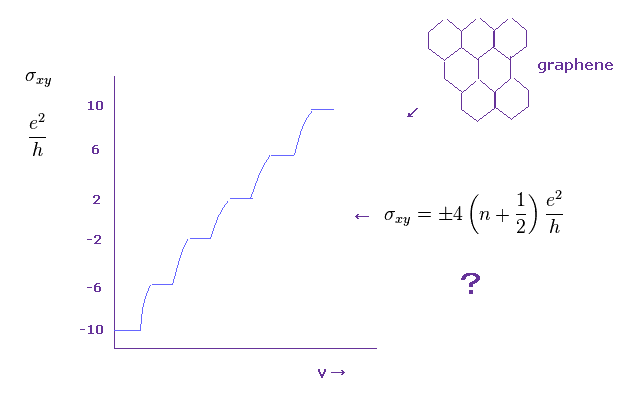
グラフェンの単層 ( 炭素 ) が 特殊な量子ホール効果を示すことが知られている。
Fig.36 や このサイトにあるように、 ホール数の整数の値 (= n ) は ±2, ±6, ±10 ... のようになる。
しかし このグラフェンの詳細なメカニズムは 未知のままである。
しかし後で このサイト、 このサイト にあるように、 0、 ±1、 ±4、や 分数 のホール数も見つかっており、Fig.36 の関係式は 正確ではないことを示している。
(Fig.37) グラフェンにおける 半整数量子ホール効果。
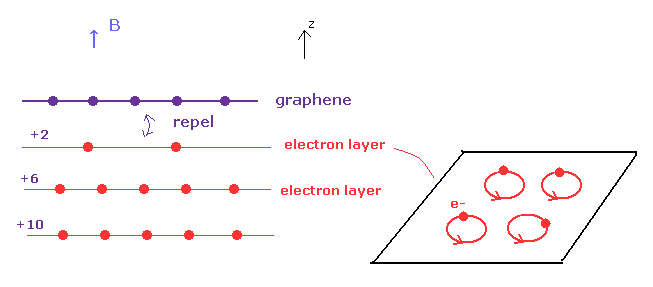
もちろん 2次元電子系といっても 電子層には 何らかの厚さがある。
グラフェンの (電子の) 単層 の影響で 他の電子が グラフェンに近づくのを 妨げられている可能性が十分にある。
このことが 最初のホール数 (= 電子密度と相関 ) が n = ±2 で、それ以降の増え方が n = ±6, ±10 となっている原因と思われる。
(Fig.38) グラフェンにおける 質量ゼロの ディラック粒子?
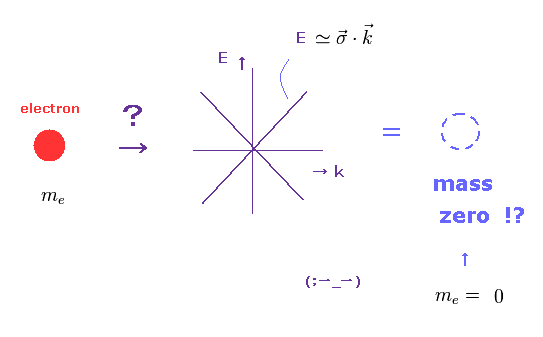
蜂の巣の電子構造を持つ グラフェンにおいても 質量ゼロのディラック電子が出現することが分かっている。 このサイト や このサイト 参照のこと。
またもや 単なる仮想の粒子を 物理現象として誤用していることになる。
ディラックコーンでは、伝導電子と 価電子バンドの間に エネルギーギャップのない状態が 2つある。
詳細な計算に関しては このページを参照のこと。
(Fig.39) 角度分解光電子分光 ( ARPES )
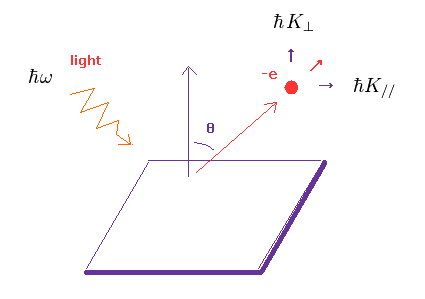
バンド構造と 質量ゼロのディラック電子を測定するためには 角度分解光電子分光 (= ARPES ) に頼る必要がある。
この ARPES の原理は 非常にシンプルである。
ある物質の表面を照射することで 光電子が飛び出してくる。
この電子の エネルギーと運動量を測定することによって、バンド構造や エネルギー分散 (= 波数とエネルギーの関係 ) を決定する。
Fig.39 では、 ħω が この光のエネルギーで、 "K" が 物質から出てきた後の 波数 (= 運動量 ) である。
(Fig.40) ARPES で、物質内の 正確な運動量を知ることは不可能である。
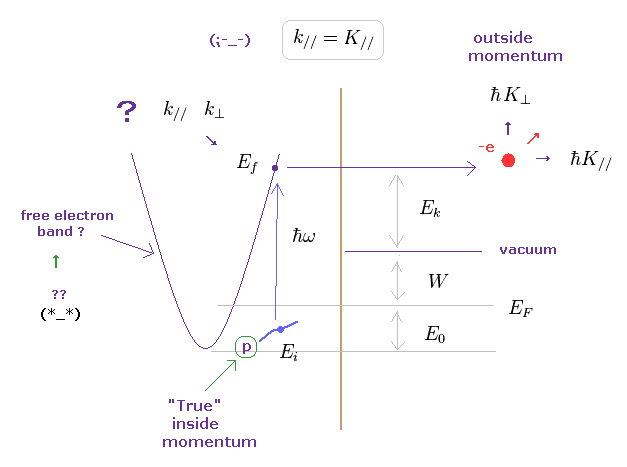
もちろん、私達が知りたいのは 物質内における 運動量 (= 小文字の "k" ) と エネルギー (= Ei ) の関係である。
しかし 基本的に はじき出された光電子のみの情報から 物質内の正確な運動量を知ることは
不可能である。
彼らは 物質外部での 光電子の運動量を 物質内部の運動量と すり替えてしまっているのである。
この甘い仮定こそが ARPES の実験における 致命的な欠陥であり、質量ゼロのディラック電子自体が 準粒子としてさえも 非常に疑わしい理由である。
(Eq.73) 外部での 運動量 (= K ) と エネルギー (= E )。
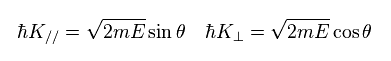
Eq.73 は 物質外部での 光電子の運動量とエネルギーである。
これらの成分は、物質の表面に対して 平行、もしくは 垂直である。
(Eq.74)
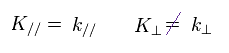
問題はここで、物質外部と内部における 電子の ( 平行成分 ) の運動量が まったく 同じであると 簡単に結論づけてしまったことである。
これは奇妙である。
なぜなら 自由電子と 低いポテンシャルに束縛されている電子の 運動量は まったく 異なる のは常識だからである。
つまり 電子が 光照射によって 外に飛び出したとき、元の運動量の情報は 完全に変わってしまっていることになる。
Eq.73 と Eq.74 から次を得る。
(Eq.75)
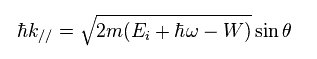
ここでは W は 仕事関数で、実験のみから得るしかない。
(Eq.76)
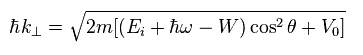
V0 も 未知のパラメーターで、これも実験から得るしかない。
もちろん、Eq.74 の前提条件が理不尽なため、ARPES に基づく 結果はすべて 疑わしいということになる。
実際に、 このサイト (p.49) にあるように 実験結果は 理論値のと 少し 異なっている。
( ex. つまり 正確には ディラックコーンは ギャップレスではない。 )
(Fig.41)

この論文 ( Science 318 766, 2007 ) では、トポロジカル絶縁体 (HgTe) における スピンホール効果が 観測されたと報告されている。
しかし この実験は 通常の スピンホール効果とは 完全に異なるものである。
もちろん、奇妙なスピン自体 直接測定することはできない。
(Eq.77)
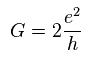
この実験では、彼らは Eq.77 に示すように 通常の整数量子ホール効果を観測したにすぎない。
スピンホールという根拠は 単に 電圧をかけることによって、両方向へ電流が流れたからというだけである。
Eq.77 の "2" が 理論値である。
しかし この論文では、この伝導度は 実は 定数ではない。
非常に特殊な状況の下で、 Eq.77 が得られただけである。
つまり この実験のみから スピンホール効果の証明とは まったく言えない。

2014/3/31 updated This site is link free.