トップページ (2電子原子も含む正確な新ボーア模型)
トポロジカル絶縁体は 本当なのか?
(Fig.1) ベリー位相とは何か ? モノポール ?

このセクションでは、ベリー位相を実際に導出する。
時間に依存するシュレディンガー方程式は
(Eq.1)
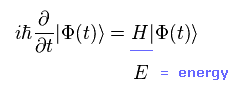
"H" は ハミルトニアンである。
ここで 次のように 新しい位相 θ を定義する。
(Eq.2)
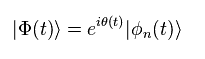
これは 標準模型のゲージ場に似ている。
"ゲージ" とは 数学上の概念で 表に現れることはできない。
しかし ここでは このゲージを最も重要な物理的概念と考えている。奇妙である。
Eq.2 を Eq.3 に代入して、
(Eq.3)
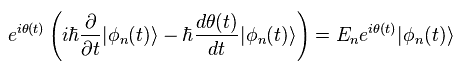
Eq.3 にあるように、 新たな位相 θ のために、この形は 通常のシュレディンガー方程式のものと 違うものになる。
(Eq.3')
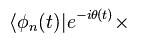
Eq.3 の左側から Eq.3' を掛けて、次を得る。
(Eq.4)
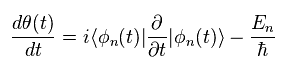
時間 t で Eq.4 の両側を積分すると、
(Eq.5)
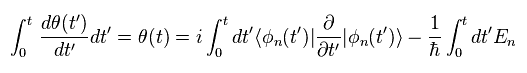
Eq.5 の θ を Eq.2 に代入して、元の波動関数として 次を得る。
(Eq.6)
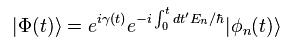
ここでは
(Eq.7)
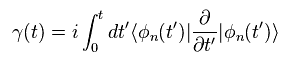
ここでは 新たな 任意のパラメーター R(t) を定義する。
この R(t) が 時間と伴に 周期的に 変化すると仮定して 時間間隔 "t" で 元の値に 戻るとする。
すると "t" の代わりに "R" を用いて この式の積分を表せる。
(Eq.8)
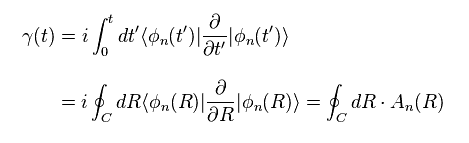
ここでは
(Eq.9)
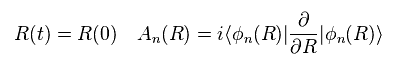
Eq.10 のように定義すると、この関係は 磁場 B と ベクトルポテンシャル A の間の関係に似ていることに気づく。
(Eq.10)
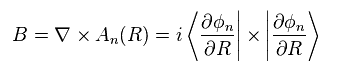
Eq.8 の γ(t) は ベクトルポテンシャルの線積分であり、 磁束 (= Φ ) に該当する。
しかし 見てのとおり これらのベクトルポテンシャル "A" と 磁場 "B" は 単なる"偽り" のものである。
Eq.10 の回転の関係式から、ベリー曲率の z 成分 Bz は、
(Eq.11)
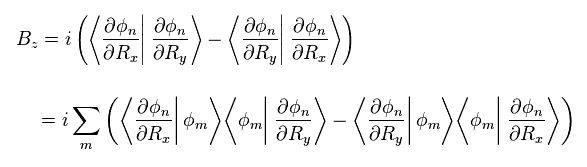
ここで 他の固有関数 φm を挿入している。
(Eq.12)
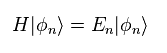
Eq.12 は ハミルトニアンと固有関数である。
パラメーター "R" で Eq.12 を部分積分すると、
(Eq.13)
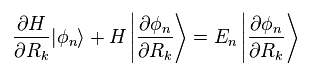
Eq.13 に 別の φm を左側から掛けて 次の関係式を使うと、
(Eq.14)
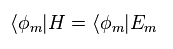
Eq.13 は、
(Eq.15)
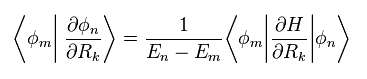
Eq.15 の複素共役は、
(Eq.16)
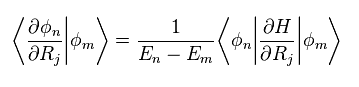
Eq.15 と Eq.16 を Eq.11 に代入すると、次を得る。
(Eq.17)
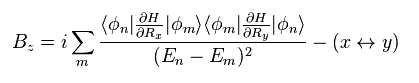
量子ホール効果では、電場 (= Ey ) の下での 二次元電子系を考える。
つまり 付け加えるハミルトニアンは "eEyy" である。
このページに示したように 波動関数の 1次の摂動は
(Eq.18)
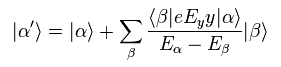
Eq.18 を用いると、 x 方向の 電流密度 (= j = -evxρ ) は
(Eq.19)
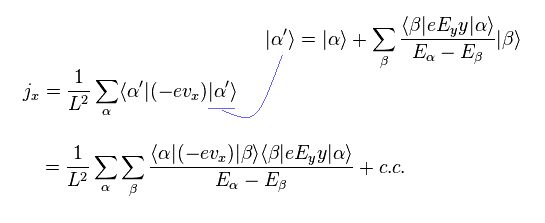
ここで "c.c" は "複素共約" の意味である。
また 二次の摂動は 無視した。
ハイゼンベルグの交換関係から、次を得る。
(Eq.20)
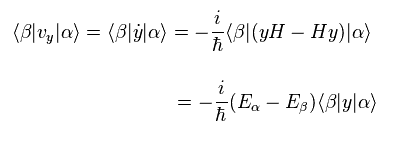
Eq.20 を Eq.19 に代入して、
(Eq.21)
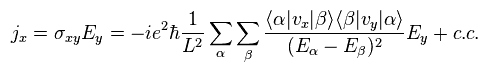
次の関係式を Eq.21 に用いると、
(Eq.22)
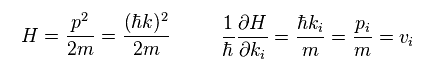
ホール伝導度を得る。
(Eq.23)
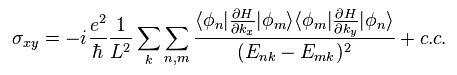
Eq.17 を用いると、
(Eq.17)
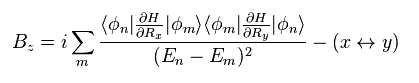
Eq.23 は、
(Eq.24)
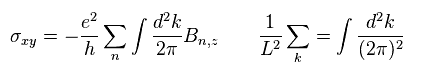
ここでは、
(Eq.25)
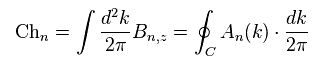
この値 (= "Ch" ) は "チャーン数" と呼ばれるものである。
このチャーン数が 整数のとき、Eq.24 のホール伝導度は 量子化されるとしている。
しかし 見てのとおり、これらのベリー位相は この現実の世界とは 何の関係もない概念である。
(Fig.2) グラフェンにおける 質量ゼロのディラック電子?
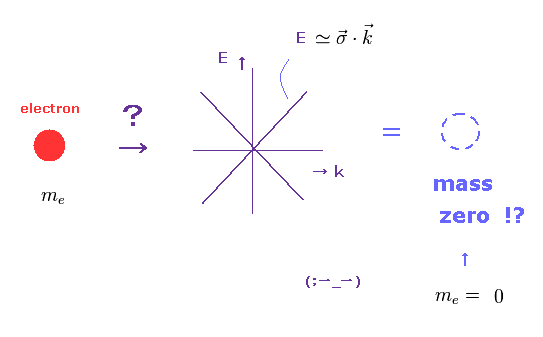
蜂の巣の電子構造を持つ グラフェンにおいても 質量ゼロのディラック電子が出現することが分かっている。 このサイト や このサイト 参照のこと。
またもや 単なる仮想の粒子を 物理現象として誤用していることになる。
このセクションでは、この質量ゼロ粒子について説明する。
(Eq.26) グラフェンのハミルトニアン。
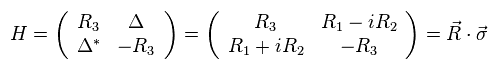
質量なしのディラック方程式のように、グラフェンの質量ゼロのハミルトニアンは Eq.26 のように表せる。
パラメーター "R" は 波数 "k" に比例している。
(Eq.27)
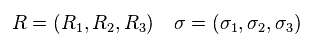
まら σ は パウリ行列である。
Eq.26 のハミルトニアンを用いると、
(Eq.28)
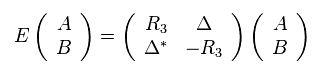
Eq.28 から、
(Eq.29)
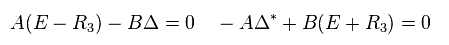
A = B = 0 の無意味な解を避けるには 次の関係式を満たす必要がある。
(Eq.30)
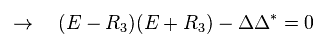
Eq.26 から、 Eq.30 は 次のようになる。
(Eq.31)
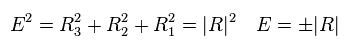
Eq.31 を見て分かるように、 エネルギーは "R" (= ここでは 波数 "k" ) に 線形に比例している。
これが この式が 質量ゼロ (= 光子のような ) のディラック電子と呼ばれる所以である。
このページのように、質量のある 通常のディラック方程式は
(Eq.32)
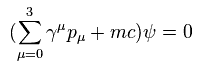
ここでは γ は 4 × 4 行列である。
Eq.32 から、ハミルトニアンは
(Eq.33)
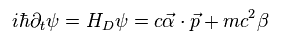
ここでは
(Eq.34)
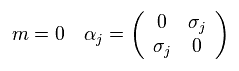
σ は 2×2 のパウリ行列である。
Eq.33 と Eq.34 から、質量が ゼロのとき、ハミルトニアンは 2 × 2 行列に分離できることが分かる。
(Eq.35)
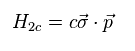
Eq.26 は Eq.35 の質量ゼロのときのディラック方程式に基づいていることが分かる。
2次元系では、 R の z 成分 (= R3 ) は ゼロになる。
(Eq.36)
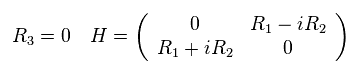
ここで、単位ベクトル ns を用いて 次のベクトルを定義する。
(Eq.37)
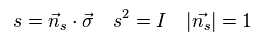
パウリ行列の反対称的な関係を用いて、
(Eq.38)
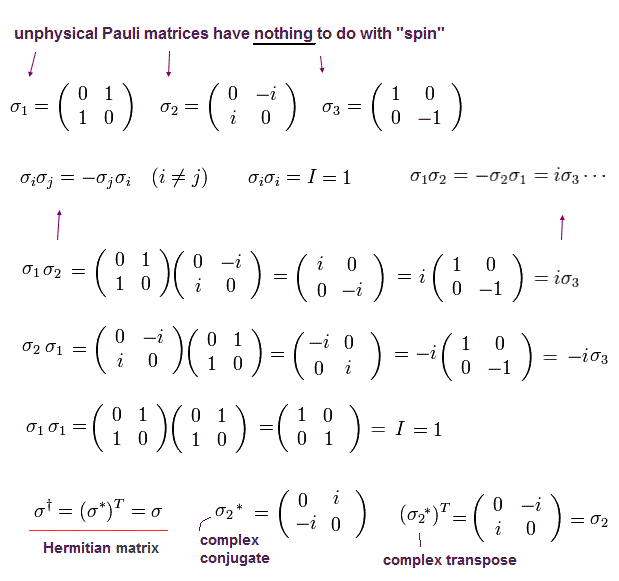
Eq.36 と Eq.37 から、次を得る。
(Eq.39)
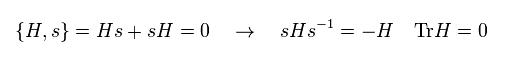
と
(Eq.40)
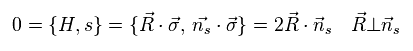
Eq.40 から、ベクトル R と n が 互いに垂直ということが分かる。
これを "カイラル対称性" という。
( もちろん、ここには 物理的なイメージは何もない。 )
Eq.26 のハミルトニアンを微分すると、
(Eq.41)
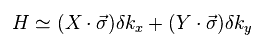
ここでは
(Eq.42)
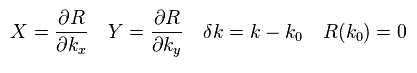
k0 の地点で 波数 R(k) がゼロになると仮定する。
伝導、価電子バンド間の エネルギーギャップがゼロ (= ギャップレス ) になる 2つの±k0 の地点がある。
(Eq.43)
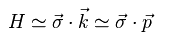
Eq.42 と Eq.43 から、このハミルトニアンは 光子様の 質量ゼロのハミルトニアンの形になる。
(Fig.3) 分数量子ホール効果 = 分数電荷 !?
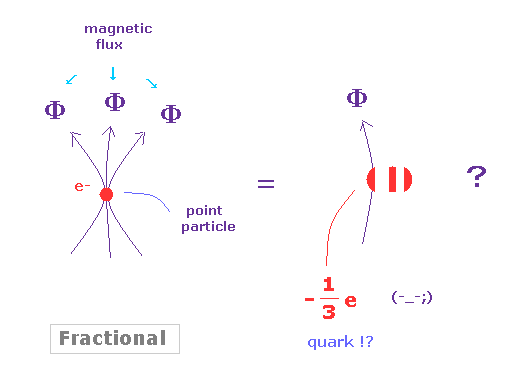
1/3 の分数の 量子ホール効果 (= FQHE ) 発見後、ラフリンが この現象を説明する 最初の理論模型を提唱した。
しかし このサイトに見られるように、この理論も 概して 物理よりも 数式的な模型に 頼りすぎていると言える。
Fig.3 に示したように、分数量子ホール効果では、点状粒子である電子が 複数の磁束を抱え込んでいることになっている。
現実的な観点からして、こんなことは あり得ない。
さらに、ラフリンの理論は 1/2 のような 分母が 偶数である現象を説明できない。
外磁場を z 方向とする。
すると、ベクトルポテンシャル A は
(Eq.44)
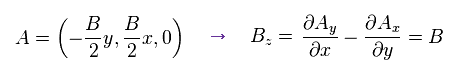
Eq.44 から、ハミルトニアンは
(Eq.45)
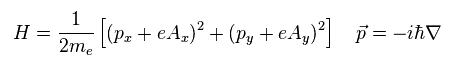
ここでは 次を定義する。
(Eq.46)
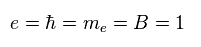
Eq.44 と p = -iħ∇ を Eq.45 に代入すると、ハミルトニアンは
(Eq.47)
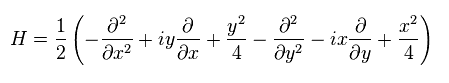
ここで 次を定義する。
(Eq.48)
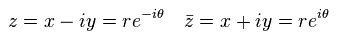
Eq.48 から、
(Eq.49)
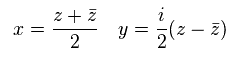
Eq.48 の z を用いて、 Eq.47 のハミルトニアンは、
(Eq.50)
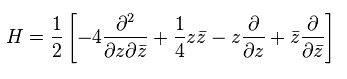
ここでは 次を用いる。
(Eq.51)
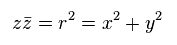
と
(Eq.52)
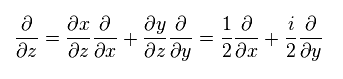
と
(Eq.53)
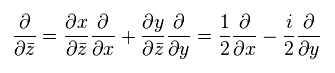
次の新たな生成消滅演算子を導入する。
(Eq.54)
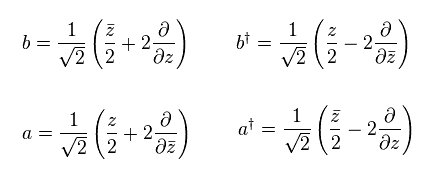
Eq.54 は 次の交換関係を満たす。
(Eq.55)
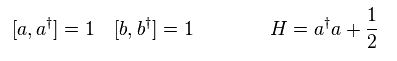
Eq.50 のハミルトニアンは 次の a†a の演算子を用いて表せる。
(Eq.56)
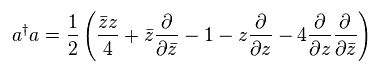
ここでは次を用いる。
(Eq.57)
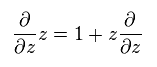
軌道角運動量演算子 (= L ) を次のように定義する。
(Eq.58)
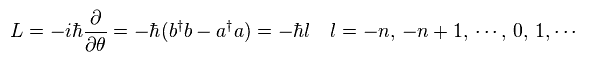
Eq.58 に示したように、 b†b と a†a の数演算子は 逆の増減作用をする。
彼らは このことを利用した。
(Eq.59)
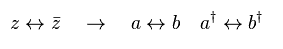
Eq.54 から、 "z" と "bar-z" を入れ替えると "a" と "b" が入れ替わることが分かる。
Eq.56 で z と bar-z を入れ替えると、t b†b を得る。
これらを Eq.58 に代入すると、
(Eq.60)
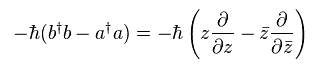
Eq.60 では、2つの項のみが残った。
( 他のすべての項は 差し引かれて キャンセルされる。 )
Eq.48 から、
(Eq.61)
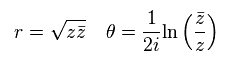
Eq.61 から、
(Eq.62)
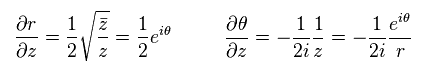
その結果、
(Eq.63)
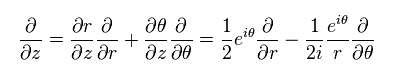
と
(Eq.64)
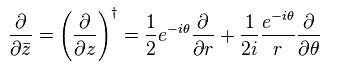
Eq.48、 Eq.63、 Eq.64 を用いると、 Eq.60 は次のようになる。
(Eq.65)
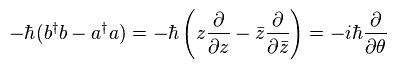
Eq.65 は 角運動量演算子であることが分かる。
固有関数が エネルギー準位 "n" と 軌道角運動量 "l" を持つと、
(Eq.66)
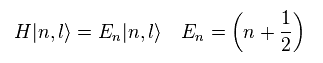
Eq.65 を考慮すると、次を得る。
(Eq.67)
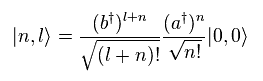
Eq.65 を見て分かるように、 "b†" 演算子は 角運動量のみを増加させる。
一方で、 "a†" 演算子は エネルギーを増加させるが、角運動量を減少させる。
(Eq.68)
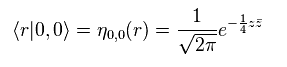
と
(Eq.69)
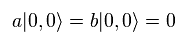
ここで エネルギーゼロ n = 0 なのに 角運動量 l がゼロでない 非常に奇妙な状態を こしらえた。
(Eq.70) エネルギー n = 0 だが、角運動量 l は ゼロでない。
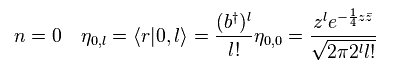
Eq.70 の状態は 完全に 非現実的である。
角運動量 l が増加するにつれ、 エネルギー "n" も増加していくのが 普通だからである。
この理不尽な誤用は Eq.65 の角運動量に対する誤解によって生じたと言っていい。
Eq.65 において、 角運動量を得るには "b†b" のいくらかの項を"a†a" でキャンセルさせなければならない。
そのため "a†a" = 0 (= エネルギーゼロ ) のとき、角運動量演算子自体が 得られないことになる。
よって Eq.70 の状態はあり得ない。
(Eq.71)
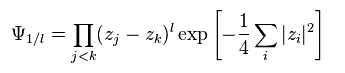
Eq.54 から、真空に作用するとき、生成演算子 b† は "z" になる。
また ここで Eq.71 の 反対称の変分関数を導入した。
奇妙なことに、 Eq.71 は エネルギーゼロ ( n = 0 ) で、かつ 角運動量 l を持つ波動関数である。
この非現実的な波動関数が 次の分数ホール伝導率につながっている。
(Eq.72)
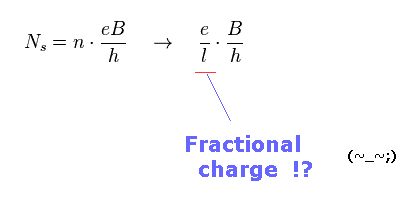
奇妙な 複合準粒子が これらの現象に出現するとしている。 つまり 現在の量子力学は 分数電荷などの仮想の粒子に そのメカニズムを丸投げしてしまっているのである。

2014/3/31 updated This site is link free.