トップページ (2電子原子も含む正確な新ボーア模型)
シュレデンガー方程式は ボーアゾンマーフェルト模型の間違いバージョンである。
電子スピンは存在しない。単なる数学上の産物。
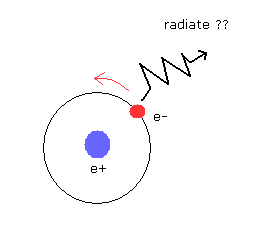
多くの量子力学の教科書は ボーアの古典的な軌道模型においては 電子が原子核の周囲を回っており いわゆる 電荷が加速されている状態のため 電磁波を放射して不安定なので間違いだとよく書かれている。
(Fig.1) ボーア軌道の電子は本当にエネルギーを放射するの ?

しかし、現実をみてみれば 明らかに 地球上の荷電粒子は "加速されて"おり かつ 安定である。
( この現実の世界で すべての荷電粒子が 永久にじっとしたままということは 不可能である。)
また このページに示したように、原子における 換算質量や相対論的な効果を考慮するとき、電子や原子核は 実際に動いており かつ加速されていることになる。
(水素原子のエネルギー準位と換算質量)
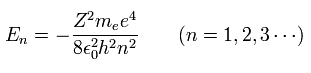
ここでは 正確なエネルギー値を得るには 質量を 換算質量 (μ) に置き換えなければならない。
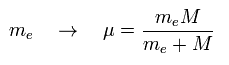
これはすなわち 水素原子の原子核と電子は 実際に 質量中心の周囲を 動いていることを意味する。
また ボーア軌道では 整数倍のド・ブロイ波長が 軌道を安定にさせているといえる。
( もし ド・ブロイ波を考えないと、水素原子の基底状態のエネルギーが いくらでも実験値より低い値をとることが可能になる。)
ところで、古典的なマクスウェルの法則は 加速される電荷が エネルギーを失うことを 本当に証明したのであろうか?
実は、そこには いくつかミスが存在する。
当時の彼の理論は -e や +e などの いわゆる電荷の量子化というものを考慮していないのである。このことが 誤った 古典的な真空のエネルギーの概念を生じさせてしまった。
(もちろん、マクスウェルの理論そのものは 非常にすばらしいもので 今でも有効であることはいうまでもない。)
(M-1) ポインティングベクトル = エネルギーの流れ ??

加速する単一電子が電磁波放射すると主張するためには、 ポインティングベクトル (= E × H ) が エネルギーの流れを意味していなければならない。
ポインティングベクトルがエネルギーの流れになるには、真空の電場エネルギー、磁場エネルギーが "本当のエネルギー" である必要がある (M-1)。
(M-2) 単一電子 -e = -dq -dq -dq -dq ... ?

M-2 に示すように、マクスウェルの世界における真空の電場エネルギー (= M-1 ) は 単一電子の導体球に含まれる
しかし もちろん 単一電子は -e より小さい電荷より構成されているわけでもないし、細かく分解することもできない。
つまり、単一電子 (もしくは 陽子 ) の場合では、真空の電場エネルギーそのものが無意味であり、ポインティングベクトルも無意味ということになる。
( 後で示すが、磁場エネルギー (電流 i × 誘導電位) も 単一電子においては 無意味である。 )
(M-3) ポインティングベクトルは電磁波ではない。
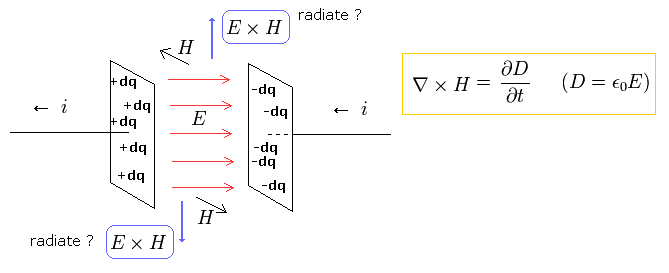
重要な点は、M-1 の 電場と磁場エネルギーは 単なる指標であり、エネルギーそのものではないということだ。
"本当の" エネルギーは 導体中、コンデンサーの板の中、ソレノイドの電線中に蓄えられており、真空中には蓄えられていない。
例えば、M-3 のコンデンサーでは、電板中の微小電荷 (= dq )間の位置エネルギーが "真の"エネルギーである。
M-3 では、電流 i が 蓄えられた電荷 (と 電場 E ) を減らす方向へ流れており、それがその周囲に磁場 H を起こしている。
ポインティングベクトル (= E × H ) の定義により、M-3 のコンデンサーは ポンティングベクトルの方向へエネルギーを放射するのだろうか?
答えは NO である。これらのエネルギーは 電線中を伝わって ソレノイドなどの他のものへ移る。( 電磁波としてではなく。) Fig.7 も参照のこと。
ポインティングベクトルは 単なる指標 であり、”本当の”エネルギーの流れではない。
もちろん、単一電子では、ポインティングベクトルは 指標でも 真のエネルギーの流れでもない。
電場 (もしくは磁場) が 光速cで 伝播することを考慮すると、遅延スカラーポテンシャル (= φ) と ベクトルポテンシャル (= A ) は、
(Eq.1)
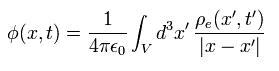
ここで ρe は 電荷密度を意味している。
(Eq.2)
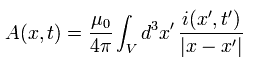
ここで i は 電流密度を意味している。
また、
(Eq.3)

つまり x 地点で 時間 t に 電場を観測したとき、 その電位は 時間 t' に x’地点から放射されたものだということになる。
(Fig.2)

Fig.2 に示したように、距離 R は近似的に
(Eq.4)

ここで x 地点は 原点 0 (= 荷電エリア ) から かなりの距離の地点とする。
(Eq.5)

すると 1/R は
(Eq.6)
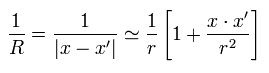
Eq.4 を使って、 x' の 荷電密度 ρe は 次のように表せる。
(Eq.7)
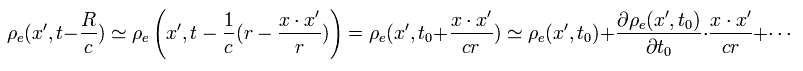
ここで
(Eq.8)
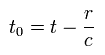
Eq.6 と Eq.7 を Eq.1 に代入して x' の2次以上の項を消すと エネルギーポテンシャルは、
(Eq.9)

Eq.9 の 第1項の 積分部分は V 領域における 全電荷 (= Q ) を意味している。
また 第2項が 次のように電気双極子 (= p(t) ) を表している。
(Eq.10)
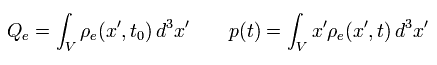
Eq.9 の 第3項の積分部分は、
(Eq.11)
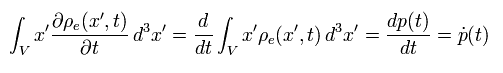
Eq.10 と Eq.11 を使うと、 Eq.9 は、
(Eq.12)
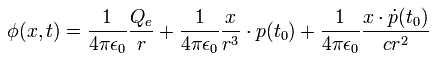
(注意: Eq.12 の x は (x, y, z) の x 成分の意味でなく 位置ベクトルを意味している。)
Eq.2 において R を r に近似的に置き換えると、ベクトルポテンシャル A は、
(Eq.13)

電荷の保存則より Eq.11 は 次のように表せる。
(Eq.14)

ここで 表面エリア S 上の 電流密度 i をゼロとしている。 (= もしくは n ベクトルに垂直 ).
Eq.14 から、 Eq.13 は、
(Eq.15)
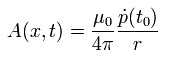
次に Eq.12 を微分することにより、電場 E を求めることにする。
( Eq.12 の第1項は 静的な場であるため 考慮する必要がない。)
Eq.12 の第2項を x (= (x, y, z) の x 成分 ) で微分すると、
(Eq.16)
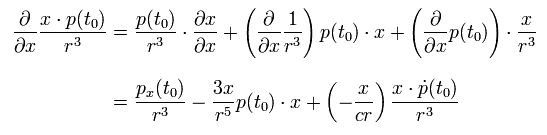
ここで次を使っている。
(Eq.17)
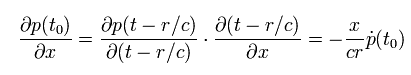
結果、Eq.12 の第2項目 の 勾配ベクトルは、
(Eq.18)

( Eq.18 の x は (x, y, z) の x 成分でなく、ベクトルを意味している。 )
同様に、 Eq.12 の 第3項目を x (= (x, y, z) の x 成分 ) で微分すると、
(Eq.19)
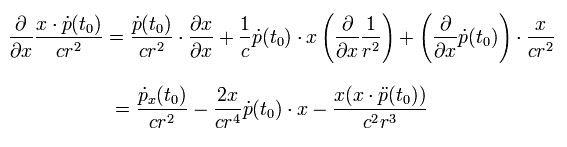
ここで Eq.17を使っている。
つまり Eq.12 の 第3項目の 勾配ベクトルは、
(Eq.20)
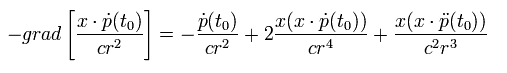
Eq.15, Eq.18, Eq.20 より、 x 地点における 電場 Eは、
(Eq.21)

ここで次を使っている。
(Eq.22)
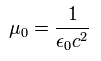
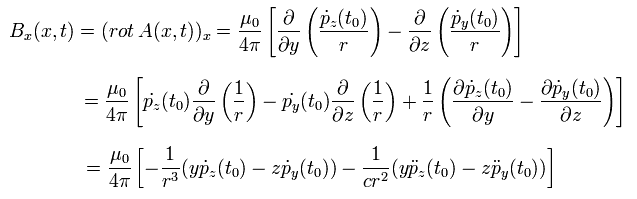
つまり 磁場 B は、
(Eq.24)
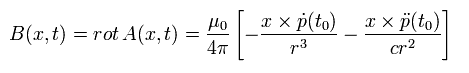
Eq. 21 より、 電気双極子の 1次 (= E1 ) もしくは 2次 (= E2 ) の微分を含んだ 変動する電場 E は、
(Eq.25)

Eq. 24 より、 電気双極子の 1次 (= B1 ) と 2次 (= B2 ) の微分を含んだ磁場は、
(Eq.26)
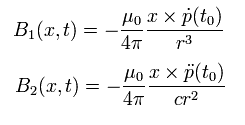
ここで x (= r ) 方向に 単位ベクトル er を定義する。
(Eq.27)
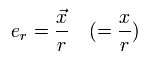
Eq.22, Eq.25, Eq.26, Eq.27 より、
(Eq.28)
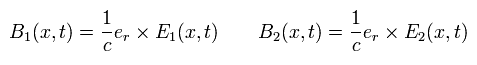
Eq.25 と Eq.26 に示したように、荷電粒子が 定常速度 (= 双極子 p の一次微分) で運動しているときでさえ それらの周囲に 電磁場は生じる。(= E1 と B1 )
しかし ボーア軌道を否定しようとする人たちは この結果を無視して 加速された双極子の部分のみ (= E2 と B2 ) をピックアップしようとしている。
もちろん、r が無限遠に近づくと Eq.25 と Eq.26 に示したように E2 と B2 のみが残る傾向にある。
しかし、現実的に 我々が 無限遠に到達することはできない。
また、運動する荷電粒子に近い部分では E2 と B2 よりも E1 と B1 のほうが 強い傾向にある ( c も考慮して )。
つまり、これらの説明によれば 定常速度で運動する 荷電粒子も 電磁波を放射することになってしまう。
これは非常に奇妙である。
マクスウェル方程式 (エネルギー放射における)によれば、ポインティングベクトル S は 電磁場における 単位時間の単位面積あたりの エネルギーの流れを表している。
Eq.25 と Eq.26 の E2 と B2 を使うと、 S は
(Eq.29)
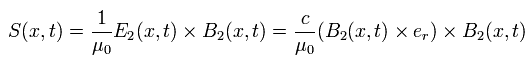
ここで 次の公式を使う。
(Eq.30)
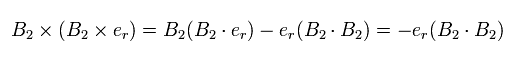
結果、
(Eq.31)
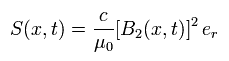
Eq.26 と Eq.31 より、 ”加速された”電気双極子からの ポインティングベクトル S は、
(Eq.32)

Eq.32 を 全球面上で積分すると "ラーモアの公式" を得ることができる。
また ”定常速度”の双極子からの ポインティングベクトル S1 は、
(Eq.33)
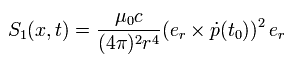
ボーア軌道では 電子は陽子の周囲を運動している。
その軌道の 短い各部分に注目すれば、電子は 自由電子のように等速運動している。
もちろん、rが無限遠の地点では 水素原子は 中性のため、電気双極子自体が ゼロになり 無視することができる。
加速された電荷による 電磁波の放射のケースでは、たくさんの荷電粒子が 同一地点を振動している (もしくは 互いに相互作用している) 必要がある。
つまり、上記の説明だけで ボーア軌道がエネルギー波を放射すると考えることは不自然である。
(もちろん、”安定した”ド・ブロイ波の概念も考慮する必要がある。)
Eq.32 と Eq.33 の ポインティングベクトルは 次の真空の電気エネルギー (= ue ) を元に導いたものである。
(Eq.34)

ところで、Eq.34 の古典的な概念は本当に正しいのだろうか?
(実際、放射される電磁波のエネルギーは その振幅よりも 振動数に関係していることが知られている。)
Eq.34 の関係式を得ようとするとき、我々は 半径 a の 導体球を用いる必要がある。
また、全電荷 Q は その球面上に 等しく分散されている。
(実際、この考え方は 非常に古典的である。なぜなら 電子 (-e) や 陽子 (+e) の電荷は 分離すること自体ができないからである!)
(Fig.3) 導体球 ( 半径 = a , 全電荷 = Q )
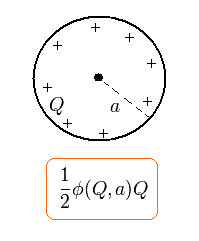
導体球の全電荷が q のとき、 その表面における 位置エネルギー (= φ ) は、
(Eq.35)

そのため その導体球の表面に 電荷 Q を与えるのに必要なエネルギーは、
(Eq.36)
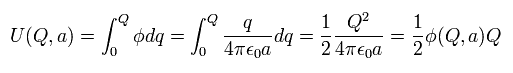
Eq.36 は Eq.34 の関係式を得るのに 欠かすことのできないものである。
しかし この導体球が 1つの電子だとすると、その電子の球に 電荷 -e を与えるのに必要なエネルギーは 無限大になってしまう !
(Eq.37)
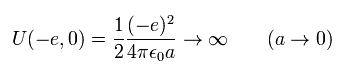
なぜなら 電子は 点粒子であり、その半径がゼロだからである。
(もちろん ご存じのとおり, 電子の電荷 -e は 分離することができない !)
(Fig.4) 単一電子 = 導体球 ??
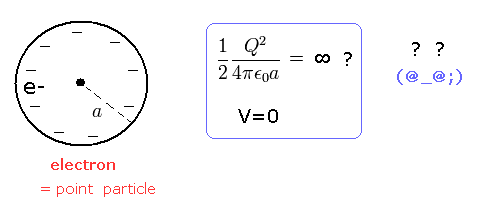
あるエリアに たった1つの電子しか存在しないとき、その相互作用エネルギー (= V ) は当然ゼロである。 なぜなら 1つしか荷電粒子がないところでは クーロン反発(もしくは引力)相互作用自体がないからである。
つまり Eq.36 の考え方は 単一電子(もしくは単一陽子)には通用しないのである!
(Fig.5) 帯電した導体球の表面
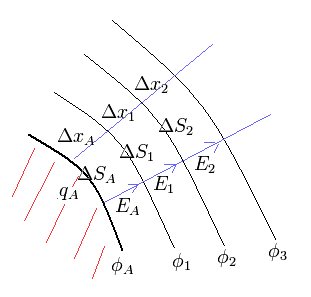
最初に 導体球の表面の ある微小領域 (= ΔSA ) について考える。
その電荷の表面密度 をqAとする。
また球の表面の電位を φA とする。
Eq.36 を使って、静電場のエネルギーは 次のように その微小区域の和になる。
(Eq.38)

ガウスの法則を使って、
(Eq.39)
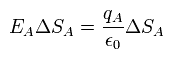
ここで EA は 表面の電場を意味している。
Fig.5 に示すように、
(Eq.40)
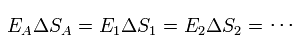
かつ
(Eq.41)
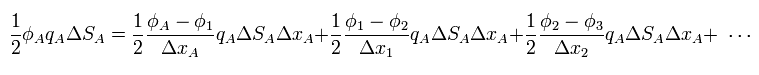
ここで ΔxA = Δx1 = Δx2 ... 、かつ 無限遠の位置エネルギー φ をゼロとする。
電場 E は ポテンシャル φ の勾配ベクトルである。
(Eq.42)
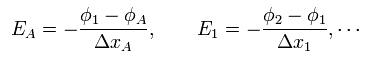
Eq.39, Eq.40, Eq.41, Eq.42 より、次を得る。
(Eq.43)
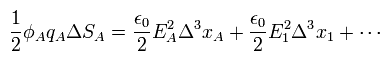
結果として すべてのエリアを足し合わせると、
(Eq.44)
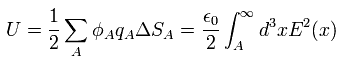
そのため 彼らは ある地点 x における 電場による真空エネルギーが次のようになると主張しているのである。
(Eq.45)

マクスウェル方程式から 次の関係式を導くことができる。
(Eq.46)

Eq.46 の左辺が 真空の全電磁場エネルギー U の時間微分であると考え、また 真空の電流密度をゼロ (i=0) とすると、
(Eq.47)
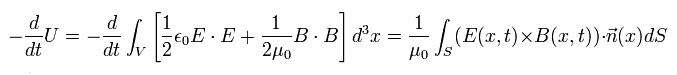
ここで Eq.47 の右辺は Eq.29 の ポインティングベクトル S を表している。
つまり この結果は ボーア軌道の水素原子の単一電子が 電磁波を放射しながら核に落ちていくことを意味しているのだろうか?
答えは NO である。
Eq.36 に示したように、静電エネルギー U は 半径 a の導体球に含まれた 無限の微小電荷 (= dq ) の間の クーロン相互作用エネルギーによって生じている。
ご存じのとおり、単一電子 (電荷 -e ) は 分離することが不可能である。そのため 単一電子(もしくは単一陽子)においては この静電エネルギー U 自体が 最初から無意味なのである。
( Eq.36 の計算方法は 単一電子においては使えないのである。)
単一電子は 電荷が -e より小さい無限の微小電荷から構成されているわけではないのである。
(Fig.6) 単一電子 (もしくは単一陽子 ) の電荷 -e = q1 + q2 + q3 ??

これは Eq.45 (かつ Eq.36) の真空エネルギー U を使うとき、各電荷 dq は 無限小(もちろん e よりも小さい)でなければならないことを意味する。
もし 単一電子もしくは単一陽子を dq として使用したいときは、全電荷 Q が 電荷 e よりもかなり 大きくなければならない。
この場合は 電荷 e をあたかも無限小 ( e → 0 ) のように扱うことができる。
これが ボーア軌道に対する誤解の根源である。
古典的なマクスウェルの法則は 電荷の量子 (= e ) を考慮していないのである。
Eq.32 において 加速された電気双極子からのポインティングベクトルを求めた。
Eq.32 において 双極子の加速方向と er の方向の間の角度を θ とする。
すると Eq.32 の r 方向の S の大きさは
(Eq.48)
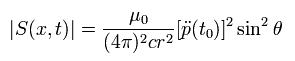
つまり、半径 r の球面上から放射する 全エネルギー流出量は、
(Eq.49)
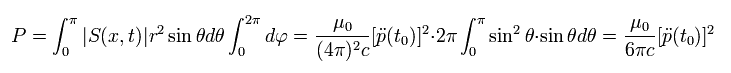
ここで次を使っている。
(Eq.50)
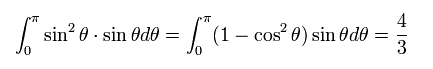
点電荷 (= e ) の 位置関数を z(t) で表すと、 電気双極子 p(t) は、
(Eq.51)
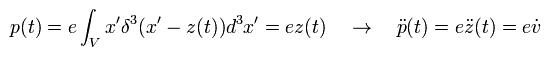
Eq.51 を Eq.49 に代入すると、 次を得る。
(Eq.52)
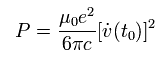
Eq.52 は "加速された" 点電荷から 単位時間あたりに放射されるエネルギーを意味している。
これを "ラーモアの公式" という。
ここでは 普通の SI 単位系を用いた。 これを cgs 単位に変えてみる。
cgs 単位では、 電磁場 ( E', H') と ポインティングベクトル (S') は、
(Eq.53)
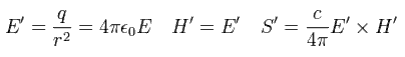
Eq.53 より、
(Eq.54)
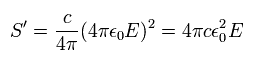
Eq.22, Eq.28, Eq.29 より、 SI 単位系における ポインティングベクトルは、
(Eq.55)

Eq.52, Eq.54, Eq.55 より、 cgs 単位における ラーモアの公式は、
(Eq.56)

Eq.52 (もしくは Eq.56) の結果をもとに、彼らは ボーアの水素原子の電子は エネルギーを放射して 原子核に落ちていくと主張しているのである。
しかし これらのケースでは 彼らは ボーア模型の水素の 通常の位置エネルギーと運動エネルギーを用いている。
( これは最初の定義に明らかに矛盾している。)
Eq.44 で述べたように、真空の電場エネルギーは 導体球に保存された 位置エネルギーに起因している。
(もちろん、この微小電荷間の位置エネルギーは 純粋にマクスウェルの方程式に準拠したものでなければならない。)
しかし 点電荷の電子においては、Eq.37 に示したように この電場エネルギーは 無限大になってしまう!
これは つまり 電子は "無限大"のエネルギーストックをその中に保有しており、エネルギーを永久に放出し続けても 決してエネルギーを失って 原子核に落ちていかないことを意味する。
(もちろん、点電荷の電子を それより小さい無限小の電荷からマクスウェルの方程式に従って作り出すこと自体が不可能だし、また それを分解することも不可能である。)
電子の質量エネルギー ( mc2 ) に等しいと仮定した 古典的電子半径でさえも 陽子ほどの大きさがある。
次に 通常のマクスウェル方程式を使用して Eq.46 における ポインティングベクトルを導出する。
マクスウェル方程式は、
(Eq.57)

ここで E と B は それぞれ 電場と磁束密度をあらわしている。
E と Eq.57 の3番目の式の内積と、 H と Eq.57 の4番目の式の内積は、
(Eq.58)
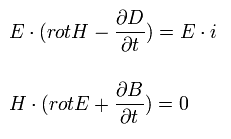
Eq.58 の 上の式から 下の式を引くと、
(Eq.59)
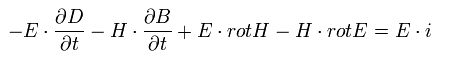
ここで 次の公式を使う。
(Eq.60)
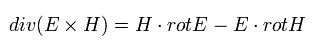
また次の関係式も使う。
(Eq.61)
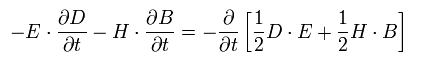
すると Eq.46 の式を得ることができた。
すでに述べたように 点電荷の電子のエネルギーストックは無限大であるため、決してエネルギーを使いきってしまうことはない。
マクスウェルの法則によれば、Eq.61 に含まれている 電磁場エネルギーは 互いに等しい。 (Eq.28 も使って。)
ここで 次の系を使って この関係式を視覚化してみる。
(Fig.7) 1つのコンデンサー + 1つのソレノイド
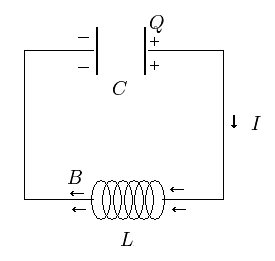
ソレノイドの 磁束 (Φ), 磁束密度 (B) と コンデンサーの2つの導体極板間の位置エネルギー差 (φ) は、
(Eq.62)
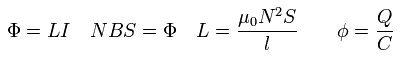
ここで C は 静電容量で、 コンデンサーの電荷 (Q) と そのプレート間の電位 (φ) の比で 定数である。
また L は ソレノイド(コイル)の "誘導係数" で、 "I" は 電流である。
N は ソレノイドのコイルの巻き数で、 l と S は それぞれ ソレノイドの長さと面積である。
(注意: 磁束 (Φ) は 普通は BS に等しい。 しかし この場合 我々が知りたいのは 誘導電圧である。 誘導電圧 (V) は コイルの巻き数に比例する。)
つまり ファラデー(- レンツ)の電磁誘導の法則で知られる 誘導電圧(起電力) (V) は、
(Eq.63)

Fig.7 に示したように、コンデンサーとソレノイドの電位の和はゼロになる。
(Eq.64)

Eq.64 より、 我々は 時間の変化にともなって コンデンサーの電荷 (Q) と 電流 (I) がどう変化するかを知ることができる。
(Eq.65)
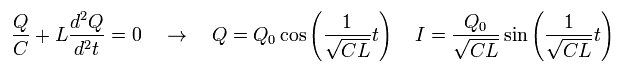
Eq.65 によれば、時間 t=0 における コンデンサーの電荷 Q と 電流 I は、
(Eq.66)

また 次の時間では、
(Eq.67)
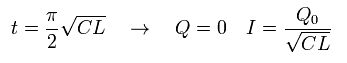
また 次の時間では、
(Eq.68)

Eq.66 と Eq.68 の時間のとき、コンデンサーに蓄えられた電荷は最大になる (= ± Q0 )。
コンデンサーに電荷 Q を蓄えるためには 次の エネルギー が必要になる。
(Eq.69)

ここでは
(Eq.70)

注意: ここの l と S は コンデンサーの長さと面積を意味している。
この結果は Eq.45 の真空の電場エネルギー密度のものと同じである。
重要な点は 我々が Eq.45 や Eq.69 の電場エネルギーを使用したいときは、その電荷が マクスウェル方程式にそって貯められたものである必要がある。
上で述べたように 電子の電荷自体は マクスウェルの方程式にそって 貯められたものではないのである。
それは 最初から存在しており、かつ分解もできない。
つまり 単一電子の周囲の電場は ポインティングベクトルのエネルギーとして使用できないのである。
また 次の関係式が導ける。
(Eq.71)
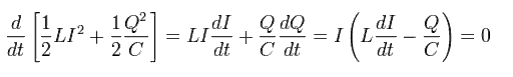
ここでは Eq.64 を使用している。
Eq.71 は (古典的な導体における) 全エネルギーの保存を意味している。
Eq.62 と Eq.57 の マクスウェル方程式を使って、次を得る。
(Eq.72)

ここでは 次の関係式を使っている。
(Eq.73)

長いソレノイドの外は、 磁場 H が近似的にゼロである。そのため NI = Hl とおける。 (Fig.8 も参照のこと。)
(Fig.8)

t=0 (= Eq.66) の時間のとき、 電流 (I) はゼロで、 コンデンサーの電荷 Q は 最大になる。
(Eq.74)
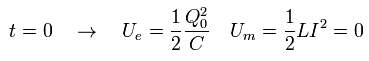
この場合は、 エネルギーはコンデンサーのみに蓄えられる。 (ソレノイドのエネルギーはゼロである。)
一方、 Eq.67のときは、 コンデンサーの電荷はゼロになり、電流は最大になる。
(Eq.75)
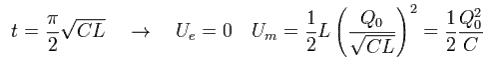
Eq.74 のエネルギーは Eq.75 にちょうど等しくなる。
結果、 Eq.72 の磁気エネルギーは Eq.69 の電場エネルギーと同じになる。
( もちろん Fig.7 の系を選んだことがこの結果につながったことはいうまでもない。 )
このページに示したように、Eq.69 や Eq.72 を 電磁場エネルギーと定義したいときは、少なくとも 2つ以上の電荷が必要である。
電場エネルギーにおいては、少なくとも2つ以上の電荷がないと、その相互作用クーロンエネルギーが生成されない。
なぜなら クーロンエネルギー = 電場 (E) × 電荷 だからである。
( つまり 単一電子では 電場を”エネルギー”と定義できない。)
磁場エネルギーのケースでは、1つの荷電粒子 (分割できないものとする) が ある軌道を回転運動していて そのスピードが変化しているとする。このとき その中に形成される磁場は変化していわゆる 誘導電位がその軌道上に発生する。
磁気エネルギーをためるには、この誘導電圧の中を 別の荷電粒子が 最初の粒子の軌道に沿って進んでいく必要がある。
つまり 磁気エネルギーの場合でも、電場エネルギーのように エネルギーは 電荷 × 電位になるのである。
1つの電子しか存在しないとき、誘導電位のみしか存在しない。エネルギーをためるには もう1つ以上の別の電荷が必要になる。
結果的に、単一電子は たとえ加速度運動していても エネルギーを放射しないのである。
電子と陽子間の位置エネルギー (もちろん運動エネルギーも考慮して) が変化したときはじめて それは エネルギーを放出 (もしくは吸収) するのである。
もちろん この結果は 実験での現象に合致していることはいうまでもない。
(Fig.9) マクスウェルの世界の 電場 (E)
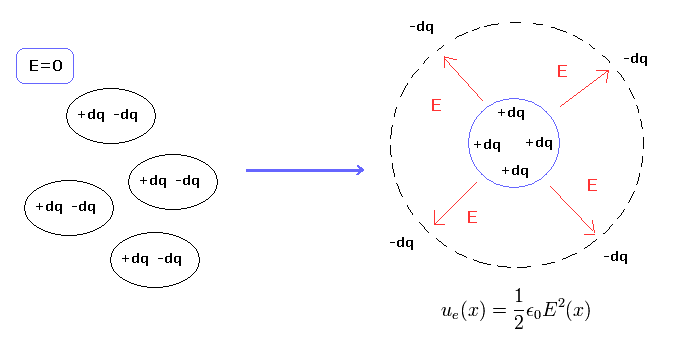
マクスウェルの世界では Eq.57 のマクスウェルの方程式のみが有効である。
(これはつまり すべての現象をマクスウェル方程式のみを用いて表現しなければならないことを意味する。)
また、マクスウェルの世界は "無限小" の電荷 (= dq ) や、電荷密度 (= ρ ) などを用いており、量子化された電荷 (= e ) は用いていない。
そのため、電場 (E) が生成されることは プラスとマイナスの微小電荷が空間上で偏って存在することを意味する (Fig.9 右)。
結果的に、電場自体の生成に Eq.36 の エネルギーが自然に必要になってくる。(これが 電場エネルギーである。Eq.44 も参照のこと。)
(Fig.10) 単一電子の世界。

一方、単一電子の世界では 電荷 (e) は "量子化"されている。
つまり、最初から 電荷 e が存在しており、要するに 最初から 電場(E) も存在することを意味する。
結果的に 単一電子の世界では、”電場”の存在は 真空の電場エネルギーの存在と 等価ではないのである。 ( ue = 0. )
(それにもちろん、我々は 単一電子をさらに小さく壊すことはできないので その中に蓄えられている”無限”のエネルギーを放出させることはできない。)
(Fig.11) マクスウェルの世界の 磁場 (B)

マクスウェルの世界の磁場では、我々は その起源として 電流(密度)i を使用する (Eq.57)。
電流 (= I ) は いわゆる "1次元の線" であり、点状粒子ではない。
つまり マクスウェルの世界では 無限小の電荷 (= dq ) が 1方向から 他方向へ ”自動的に”"安定して"供給されていることになる (Fig.11)。
電流 I が増加したとき、その周囲の磁場は増加し、それは 誘導電圧 (V) を発生させる。その V は増加する磁場を弱めようとするものであり 結果的に電流を増加させないようにはたらく。
つまり 我々が 電流を増加させようとすると "自然に" エネルギーが必要になってくる。(エネルギー = 誘導電圧 × dq )
これが いわゆる Eq.72 の "磁気エネルギー" である。
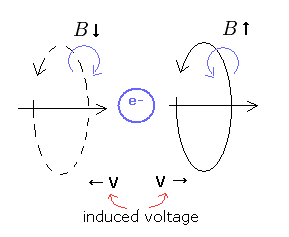
一方、単一電子の世界では 電子が1つしかない。
そのため 電流を生じさせようとしても、”1次元の線の電流 I ” を生じさせることができない。
電子の前方では、電子が近づくため 磁場 (= B ) が 増加する。
結果的に 誘導電圧 V が その磁場 (かつ電流) を弱める方向に生じる。
しかし 電子の後方では、電子が遠ざかっていくために 磁場が減少する。
そのため 磁場 (かつ電流) を強めようとする 誘導電圧が生じる。
これらの誘導電圧は逆であり 互いに打ち消し合う。
結果的に、単一電子の世界では 磁場を生じさせるのに 磁気エネルギーが必要ないのである。
もちろん、磁場自体は 電場によって生成される。そのため Fig.10 のように 電場自体にエネルギーが存在しないとき、磁場にもエネルギーが存在しないことになる。
結果、Eq.61 の 電磁場エネルギー自体が 単一電子の世界では存在しないため、Eq.46 の ポインティングベクトルが意味のないものになってしまう。
"ボーアモデルの水素原子の電子が エネルギーを放射して核に落ちていく" という考えは おそらく ”非常にイメージしやすい”ボーアモデルを 学生たちに あきらめさせようとした人々によって マクスウェルの時代よりも後に 作られたものであろう。
マクスウェルの理論そのものは もちろん 電荷の量子 (= e ) を考慮すれば 今も有効であることはいうまでもない。
Eq.72 の磁気エネルギーは少し思い浮かべるのが難しい。
ここで 単一の剛体球が加速しているとする。
また Fig.13 に示したように その剛体内に 微小電荷 (= dq ) が分布しているとする。
(Fig.13) 単一電子 = 剛体球?

もちろん、単一電子は剛体球ではないので、Eq.61 の電場エネルギーは 単一電子のケースには使えない。
つまり、ポインティングベクトルは 単一電子の世界では エネルギーの流れを意味していないことになる。
誘導された磁場 (= H ) は Eq.57 の三番目の式や Fig.13 の式 を満たしている (アンペールの法則)
Fig.13 のアンペールの法則の式の 1番目と2番目の項は それぞれ独立している。
2番目の項は とても長い 1次元の電流 i を使用している。
このケースでは、たとえトータルの電場 (E) の合計がゼロでも、電流 (= i ) は存在でき、かつ磁場をその周囲に引き起こす。
( 長いソレノイドの場合も同様である。プラスとマイナスの電荷が同数あり、トータルの電荷が中性のときでさえ、電流 i は存在できる。)
単一荷電粒子のケースは Fig.13 の 1番目の項に当たる。
つまり、移動している荷電粒子の周囲の 変動する電場 (= E ) が 磁場を引き起こす。
正確に言うと、我々は 同じ磁場を 2回重複して数えてはならない。よって Fig.13 の 2番目の項の電流 i は 定常な電場を生じる電流に限定しなければならない。
しかし Fig.13 の 剛体球が 導体球だとしたら、その中の電場 (E) は 常にゼロになる。
結果、磁場 (= H ) は電場によって誘導されず、誘導電圧 V も起らない。
また、微小電荷 (= dq ) が 剛体球の内部に固定されて 剛体球とともに常に動いているとすると、剛体球の内部の電場 (= E ) は Fig.13 に示した通り 常に一定になる。
( なぜなら 球内の 微小電荷間の 位置関係 が 変化しないからである。)
つまり 例え 剛体球が加速していても 誘導磁場や 誘導電圧が その内部で生じないことになる。
すでに述べたとおり、磁場エネルギーは 誘導電圧 V × 電荷 (= dq ) もしくは電流 である。
よって 加速している単一電荷は 磁場エネルギーも持っていない。
(磁場エネルギーを持つには 少なくとも2つ以上の分離した荷電粒子が必要である。)
結論からして、”加速している ボーア模型の電子が 電磁波を放射して 核に落ちていく”という考えは 例え ド・ブロイ波長を考慮しなかったとしても、完全に間違った考えなのである。
すでに述べたように、Eq.61 の電場エネルギーは 電子自体を破壊して その中の無限大のエネルギーを放出できないので、単一電子の世界では無意味である。
( つまり ボーアモデルの加速している”壊れない”電子は エネルギーを放出しない。)
また 磁場は 電場によって生じるので 磁場エネルギーもなしということになる。
( 世界には 磁荷は存在せず、電荷しかない。)
(Fig.14) 磁場=電場。
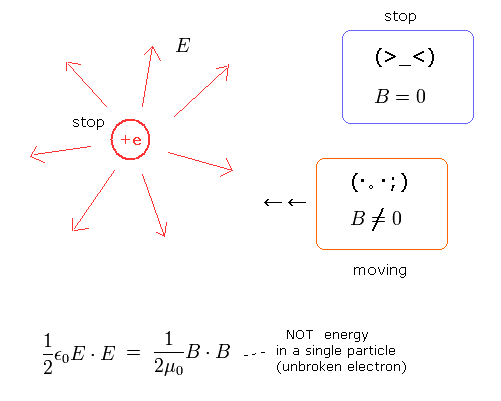
相対論によれば、磁場と電場は 観測者の視点によって 見えたり見えなかったりするもので、基本的に同一の存在と見なしている (= 等価原理 )。
Fig.14 では、電荷 (+e) は 静止している。そのため 静止した 観測者からは 磁場 (B) は観測されず、電場 (E) のみ感じることができる。
しかし、動いている観測者からの視点では 磁場が生じているように見える。
つまり、磁場や電場は 同一のものの違った見え方だということである(観測者の動きに応じた)。
よって、電場にエネルギーがなければ、磁場にもエネルギーがないことになる。
(Fig.15) 磁場=電場。

Fig.15 では、電荷が 速度 v で動いている。
この場合では、じっとしている観測者の視点からは、磁場が見える。
しかし、同じ速度 v で運動している観測者からしたら、磁場を感じることはできない。(彼は電場のみ感じる。)
これは 根本的に 磁荷というものが存在しないという事実に起因する。
磁場は 2つの電場間の 相対速度によって生じると言っていい。
特殊相対論は そもそも最初は これらの電磁気学の現象を基に作られたものである。
しかし、エーテルを否定してしまったために、クーロン相互作用を表すのに 非実在の”仮想光子”なるものに頼らざるを得なくなってしまった。
また、それは”時間の遅れ”のような非常に奇妙な概念も用いている。
これらの点は修正する必要があると私には思う。
もし、エーテルを否定したとしたら、我々は 電磁場を違うもので定義する必要がでてくる。ここで いわゆる "仮想"光子なるものがでてくる。
つまり たとえ 単一電子が 破壊できないもので その中の無限のエネルギーを放出できなかったとしても、我々は その単一電子の周囲の電場に ”エネルギー”を与えなければならない。
なぜなら すべての電場は 単一電子 (もしくは 陽子) の電場の合計で表せるからである。
このページの Eq.64 に示したように、量子電磁力学における電磁場のハミルトニアン (= エネルギー) は、
(Eq.64')
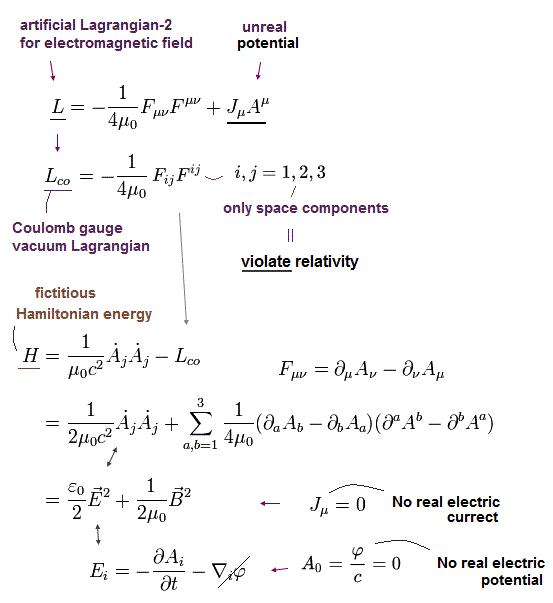
もちろん、クーロンゲージでは ローレンツ不変性が破れている。このことが "非実在の" 仮想光子を クーロン力に使わざるを得ない結果となった。
この矛盾(と 上で述べた 奇妙な電場エネルギー )をやめるには、我々は 電磁場を表すのに ”光子という粒子”を使うことをあきらめなければならない。( これは "量子電磁力学" をあきらめることと等しい。)
このページに示したように、場の量子論にとって マクスウェル方程式、電場 (= E ), 磁場 (= B ) の概念は 欠かすことのできないものである。
そのため Eq.64' の結果がでたことは QED では 自然であるといえる。重要な点は 単一電子の世界でさえも Eq.64' が 電磁場エネルギーを表しているか 判断しなければならないことである。
QED では 源である単一電子からでている その周囲の電磁場を (仮想)光子として切り離して扱っている。
つまり QED では この判断が適切にできないのである。
すべての真空は "仮想"光子でみたされている?
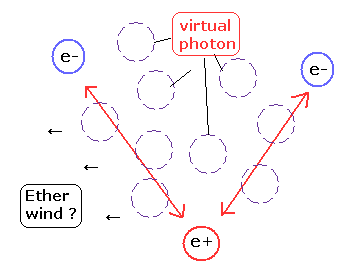
また このページで示したように、もし 真空が (仮想)光子で満たされていたとしたら、それは いわゆる "エーテルの風" を生じさせてしまい、これは 特殊相対論に矛盾することになる。
(なら もし 誰かが”仮想”光子は実在しないので大丈夫だと言ったとしたら、さて じゃあ いったい "実在の"クーロン力は 何によって起きているのだろうか? これは非常に奇妙である。)
Fig.13 では、各微小電荷の視点からは 電場や電流の変化が感じられない。そのため 誘導電位は各電荷の部分で 起こらないことになる。
電流 (= i ) の場合は 他に注意すべき点がある。
(Fig.16) 電流=プラスとマイナスの電荷の相対的な運動。
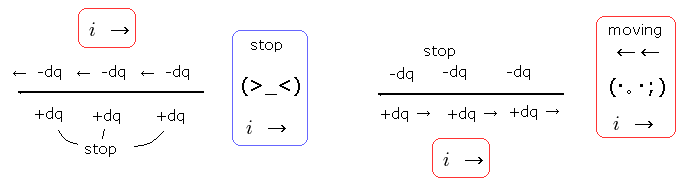
ト―タルの電場がゼロのときでさえ、電流 (= i) によって 磁場を生じることができる。
電流は たくさんの プラスとマイナスの電荷を含み、それらは 互いに逆の方向へ進んでいる。
つまり、電流が増加するにつれて プラスとマイナスの間の 衝突が増加することになる。
これが その周囲の磁場の増加につながる。
結果的に 電流 i の周囲の磁場を増加させるにはエネルギーが必要になってくる。
Fig.16 に示したように、電流 i は 観測者の視点と独立しており、この点は 電場のときとは違う。
なぜなら、観測者の視点に応じて プラスとマイナスの電荷間の 相対運動 = 差は変化しないからである。
点電荷の世界で Fig.13 の 2番目の項を 磁場の源として使いたいときは、点電荷周囲の無限小領域に限定する必要がある。
(この無限小領域では 点粒子が”非常に長い”電流のように見えるからである。)
1つの点電荷しか含まないエリアのほとんどは、磁場は Fig.13 の1番目の項によって生じる。
正確に言うと、マクスウェル方程式において、同じ磁場を2回重複してカウントしてはいけない。
Fig.13 の 2番目の項は 定常な電場を生じる 電流 i に限定する必要がある。
つまり、動いている点状の電子は マクスウェル方程式における 電流 i として使用できないことになる。
(Fig.17) 電流 = 電荷の安定供給

実際には、電流 i は 電場 (= E ) を変化させ、それが 周囲に磁場 (= H ) を起こす原因となる。
プラスの電荷が 右方向へ流れているとき、このプラスの電荷は 右端に溜まっていくことになる ( Fig.17A )。
結果、電場 E が変化していく。
しかし マクスウェル方程式の 電流 i は 両側から 常に プラスとマイナスの電荷を安定供給されている ( Fig.17B )。
つまり 全電場は変化しないのである。これらの時間差が 磁場を起こす原因となる。
もちろん、円形の閉じた電流回路では、2つの 互いに逆方向の電流が 同時に存在する。
結果的に 電流 i においては 全電荷の中心は動かないことになる。
単一電子の世界においては 同時に 正反対の方向の電流を生じさせることは不可能である。
その結果 単一電子の世界では、変動する電場が 磁場を生じさせる 唯一の手段となる。
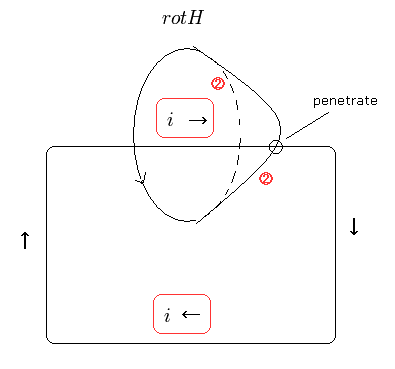
(Fig.18) 単一電子の世界では ポインティングベクトルは 電場 (= D ) の時間変化から得られる。
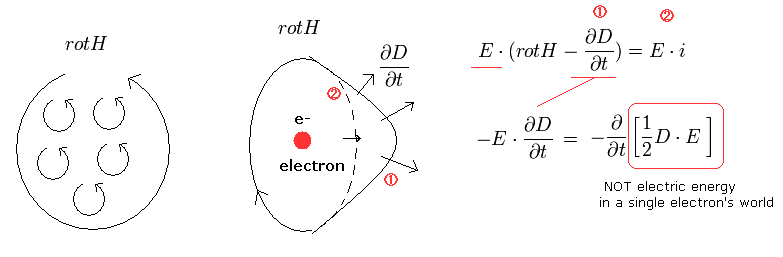
Fig.18 に示したように、rot H は 閉曲線 H に囲まれた任意の曲面上に含まれる 小さな円の総合計として表される。
この曲面は 同じHに囲まれる限りどれを選んでも同じである。
単一電子の世界では 電流 i は 不連続 のため、rot H は 必ず 電場 D の時間変化で表すことができる。これは Fig.18 の 1 番目の項にあたる。
( つまり 単一電子の世界では 電流 i を使用する必要がないのである。 )
上で述べたように、単一電子は 無限小の電荷の集合体でもないし、またそれらに分解することもできない。
よって Eq.45 の電場エネルギーは意味をなさない。
Eq.58, Eq.59, Eq.60 に示したように、ポインティングベクトルの導出には 電場エネルギーを必要とする。
つまり ポインティングベクトルは 単一電子の世界では無意味ということになる。
(Fig.19) "連続の"電流 i における rot H
一方で、連続の電流 i においては、rot H に囲まれた 曲面は必ず 電流 i を含む。
つまり Fig.18 の 2番目の項がこのケースでは有効である。
上で説明したように、磁場を増やすのに必要な (Eq.72 のような) 磁気エネルギーは 電荷 × 誘導電圧 V で表される。
Fig.18 の単一電子の場合は、増加する各磁場 (H) は それによって囲まれる任意の局面上の rot H の小さな円の合計と同じ意味である。
そしてこの局面は Fig.18 に示したように 電荷 (= e-) を含む必要はない。
この局面上では 変動する磁場によって 誘導電圧が生じる。
しかし この局面は 電荷を含まないので 磁気エネルギーが必要ない。
( 磁気エネルギー = 電荷の流れ × 誘導電圧 V )
一方、Fig.19 においては、ゼロでない 任意の rot H によって囲まれた局面は 必ず 電流 i を含む。
そして 磁場を上昇させるために 電流 i を増加させた地点では 誘導電圧 V が生じる。
結果として、Fig.19 において 磁場を増加させるのには 磁気エネルギーが必要となる。
(Fig.20) "連続の"電流 i では、電場エネルギーが有効である。

もし コンデンサーがこの電流回路に含まれるとき、Fig.20 のように このコンデンサーを含むような 曲面 (= 1 ) を選ぶことができる。
この場合では rot H は 電場 D の時間変化として表すことができる。
Eq.69 に示したように、コンデンサーの電場は 電場エネルギーを意味している。
なぜなら Fig.20 の電流回路は 無数の プラスとマイナスの微小電荷から成り立っているからである。
Fig.7 では コンデンサーの電場エネルギーの減少分が ソレノイドの磁場エネルギーの増加分に等しい。
よって Fig.7 においても ポインティングベクトルによるエネルギーロスはゼロとなる。
いずれにしろ、電磁場を正確に説明するためには 単一電子(もしくは 陽子)の周囲のクーロン場を 使わざるを得ない。 なぜなら すべての電磁場はそれらの合計で表せるからである。
クーロン力 や 重力 などの ”逆二乗の法則” を説明するには 我々は 相対論を見直さなければならない。
そして もう一度 ニュートン力学、マクスウェル電磁気学 (+ ド・ブロイ理論 ) に戻って考え直す必要があると私は思う。
相対論は量子力学とそりが合わないという人たちがいる。
しかし実際は、それらは非常に緊密な関係にある。
波動関数における "実在性の消失" は 特殊相対論を意味する。
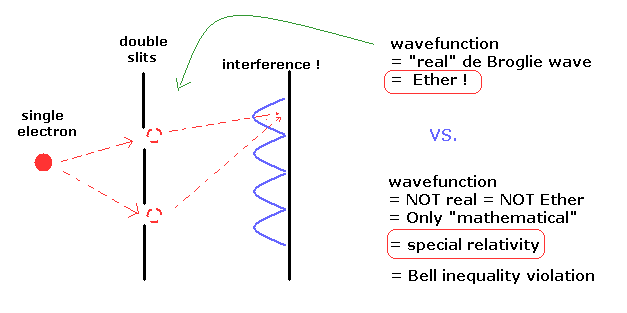
単一電子だけでも 二重スリットにおいて 自分自身と干渉することができる。
一般的な量子力学的解釈によれば、この電子の波動関数は 単なる”数学的な”確率振幅を意味し、非実在性のものと解釈している。
( もし この波動関数を実在性のものと解釈すると、電子は 波動関数が収縮したときに 光速を越えなければならない。)
このページに示したように、量子力学のベルの不等式の破れによれば、彼らは 波動関数は ”非局所的”かつ”非実在的”なものと主張している。
もし、波動関数が "実在性" のものとしたら、この実在の波動関数は 真空中の " エーテル "の中を伝わる 一種のドブロイ波と解釈できる。
つまり、もし 我々が 波動関数のリアリティー (= " エーテル " ) を認めたとしたら、相対論を否定したことになる。
結果的に ベルの不等式の破れに示されるような 波動関数の "非現実" かつ "非局所性" の解釈は " 特殊相対論 " を支持していることになる。
( 奇妙なことに 非局所=特殊相対論 ということになる。)
非常に重い W ボソンは エネルギー保存則を完全に破っている。
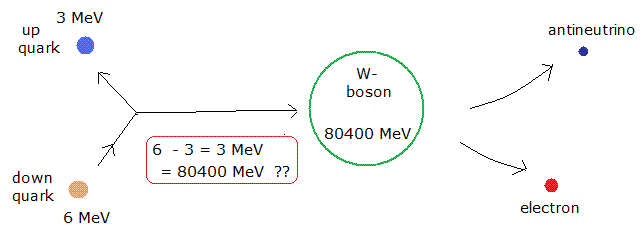
このページに示したように、 陽子の80倍もの重さのある W ボソンを使用する β崩壊は エネルギー保存則を破っている。
ダウンクォークとアップクォークのエネルギー差は たった 6 - 3 = 3 MeV である。 しかし 加速器内の W ボソンは80400 MeV ほども エネルギーがある !
彼らは この奇妙な現象を 時間とエネルギーの不確定性原理 を用いて説明しようとしている。
つまり ボーア・ゾンマーフェルト模型が正しく、シュレディンガー方程式が間違いとすると、不確定性原理も当然 間違いということになる。
( シュレディンガー方程式は ボーア・ゾンマーフェルト模型の間違いバージョンであるも参照のこと。)
結果的に ボーア・ゾンマーフェルト模型が正しいとすると、この重い W ボソンを用いる 標準模型も誤りということになる。
上で述べたように、特殊相対論は エーテルを否定しているので クーロン力を表すのに " 仮想光子 " を使っている。
この仮想光子は 相対論的因果律とエネルギー保存則を破っている。
なぜなら たとえ我々が何のエネルギーも その仮想光子に与えなくとも あるエネルギーを持った仮想光子が真空から出現することができるからである。
( そして 標的の荷電粒子のところで 消える。)
もちろん この過程は 不確定性原理を用いて説明しなければならない。
結果的に 特殊相対論 = 仮想光子 = 不確定性原理 とうことになる。
よって 不確定性原理が間違いだと 特殊相対論も間違いということになる。
クーロン (重力) の関係式は ローレンツ変換で 変わってしまう。

特殊相対論によれば、重要な式はローレンツ変換において 不変でなければならない。
しかし クーロンや重力の関係式は 中心電荷や中心の星を ある意味 特別視しているため ローレンツ変換で 変わってしまう。
そのため クーロン関係を表す クーロンゲージでは ローレンツ不変性は破れている。
( 奇妙なことに 光子のゼロ成分である スカラー光子は ”非実在”のものである。)
我々は 仮想光子を使用して クーロン関係を "近似的なもの" として扱うことになる。しかしこれは一種の”ごまかし”だろう。
しかし、重力においては この ごまかし が通用しない。
なぜなら 一般相対論によれば 重力は 時間と空間を支配する "根本的"なもの だからである。
そのため 一般相対論が正しい限り 我々は重力を表すのに いわゆる "余剰次元" に頼らなければならない。
もし 地球に引っ張られ かつ 一緒に動く エーテルを認めたとすれば、地球によって曲げられる光や 影響をうける GPS などを説明できると考えられる。
( 実際には GPS の時間の補正は かなり複雑である。大気の状況など 様々な要素がからんでいる。)
GPS の時間は ある原子より放射される 光の振動数を利用しているが これは 動くエーテルに影響を受ける可能性がある。
------------------------------------------------------------------------
上で述べたように、エーテルを否定したら 単一電子の周囲の電磁場を (仮想)光子を使って表さなければならない。
もちろん、マクスウェル方程式は 量子電磁力学 (QED) においても 欠かすことのできないものである。
もし マクスウェル方程式に基づいてエネルギーを計算したとしたら、Eq.64' のエネルギーの結果は自然に導ける。
結果として、QED の光子は ポインティングベクトルに見られるように 単一電子の世界を正確に説明することができないといえる。
( また それらは 特殊相対論に矛盾する "エーテルの風"を生じてしまうおそれがある。 )
(Fig.21) 電場は エーテルのゆがみが原因か ?
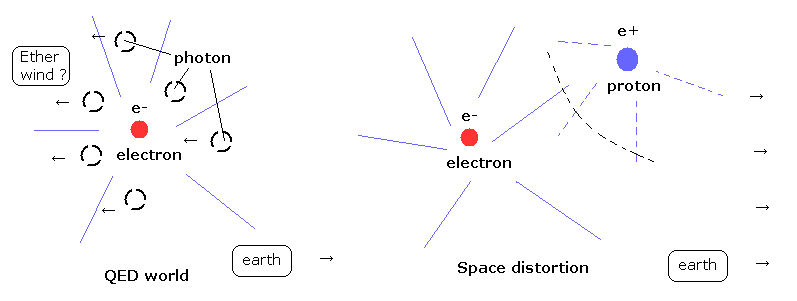
ところで、”エーテル”や”クーロン力”とは一体何かと問いたいところである。
( ここでは "数学上"の世界にのみ有効な 異次元世界のような 非実在性のモデルを忘れることにする。)
空気や水などの媒質は 互いに分離した粒子より成り立っている。
( もちろん、水や空気の各分子は "プラス"の陽子と "マイナス"の電子より構成されているが。)
しかし 固体の媒質の構成成分は 互いに結び付いている。
今のところ、エーテルの各成分が 互いにゆるく結びついているか、離れているか 判断することはできない。
(Fig.22) 電子と陽子 (陽電子でなく) のペアの生成が自然である。
ご存じのとおり、マイナス (-e) と プラス (+e) の電荷の大きさは同じである。
つまり、マイナスの電子とプラスの陽子が同時に生成されたと考えるのが自然だといえる。
このページに示したように、陽電子の存在は エネルギーの生成場所に関して自己矛盾を含んでいる。
また 我々は どうして すべての反粒子のみが消え去ったのか 未だに満足に説明することができない。また どうして 各反粒子が その対の粒子より 少しだけ少ないかも説明できない。
この "現実の"世界では たくさんの "安定な" マイナスの電子とプラスの陽子 (陽電子でなく) が存在し、かつ互いに引き合っている。
つまり 電子の "真の"パートナーは 陽子であると考えるのが自然と言える。
マイナスの電子と プラスの陽子の質量が異なることは 不思議でもなんでもない。
( むしろ 電子と陽電子のように 質量までぴったりしていることの方が不自然である。)
電子と陽子の安定性を説明するには、それらのペアを形成するのに 何らかの エネルギー的な閾値について考える必要がある。
例えば、非常に安定なヘリウム原子は 核融合によって 2つの水素原子より 生成される。
安定なヘリウム原子の生成時には 大きなエネルギーが放出される。
しかし 核融合反応には 非常に高い温度が必要であり、これが この反応の "閾値"にあたる。
おそらく、格融合のように、電子と陽子のペアの生成には 非常に厳しい閾値が必要だろうと推察される。
電子どうしの反発力や 電子と陽子の引力などを考慮すると、マイナスとプラスの電荷は エーテルの密度の違いを生じさせる何かと考えられる。
( 電子と陽子の質量差が このことに関係している可能性もある。)
おそらく、重い陽子が その周囲のエーテルを凝集する傾向にあり、軽い電子が その残りのようなものと考えられる。
( もちろん、エーテルの "偏り" は それらの間に バネのような原理で 引力(もしくは斥力)を生じさせると考えられる。)
( エーテルが十分あったり 各エーテルの方向がそろったりなどの ) ある条件のもとでは、それらは凝集できると思われる。
また 核融合においては ある閾値を越えると 形態変化を少し起こし、凝集傾向の陽子が さらに 他の陽子 (+ 一部の電子) と凝集する。
(Fig.23) 電磁波は エーテルの”偏り”の伝播である、

結果として、電磁波は エーテルの密度の偏りの伝播のようなものと考えられる。
縦方向の伝播は ド・ブロイ波のような 縦波の関係式がからんでいる。
また 横方向は電場を意味しており、これは エーテルの密度の偏り (勾配)と関係していると思われる。
( その周囲になんらかの誘電体が存在するとき、エーテルの勾配が弱められ 伝播スピードに影響すると考えられる。)
もちろん、現在の時点で このモデルはまったくの推測にすぎない。
もし 誰かが もっとすばらしい "実在性の" クーロン場モデルを示してくれたとしたら、非常に喜ばしい。
また いわゆる "重力" は たくさんのプラスとマイナスの電荷の集合体全体による 引きずり効果のようなものと考えられる。

2012/2/17 updated This site is link free.