トップページ (正確な新ボーア模型)
おかしな 超微細構造の解釈
QED の異常磁気能率のトリック (15/1/4)
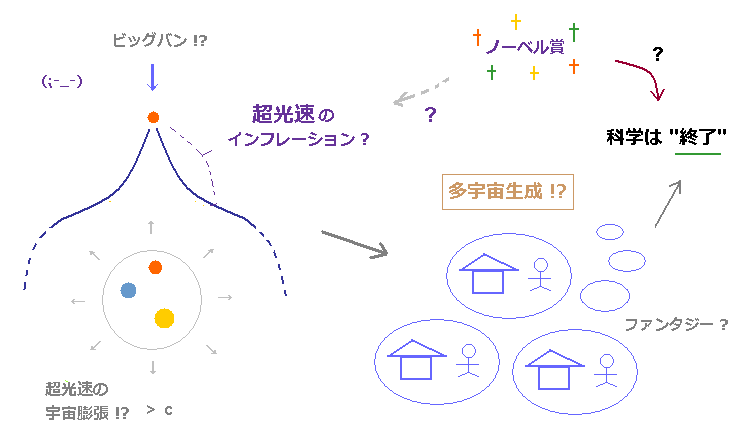
(Fig.1) 超光速 (= あり得ない ) のインフレーション、多宇宙 は 科学の終焉を意味する。

最近 原始宇宙の インフレーションの 証拠が見つかったというニュースが飛び交った。
まだ、確たる証拠とはなっていないが、現在の物理界は この 明らかに、"ファンタジー" と言えるインフレーションを公式見解にしようと必死である。
このインフレーション理論では 私達の宇宙が ビッグバンの時に 光速よりも はるかに速い速度で 急膨張し、 その過程で 因果の破れた 多数の子宇宙 が生成されたとしている。 このサイト や このサイト を参照のこと。
残念ながら、もしこのあまりにも現実離れしたインフレーションが ノーベル賞などをとってしまったとしたら、私達の科学の進展において 致命的な停滞を招くことになってしまう。
またそれによって、物理学者達が 生涯にわたって 非実在的かつ 架空の概念を追い続けるという恐ろしい状況になることは必至である。
(Fig.2) インフレーションのかすかな証拠が 137 億年も その状態を保てた !? 本当 ?
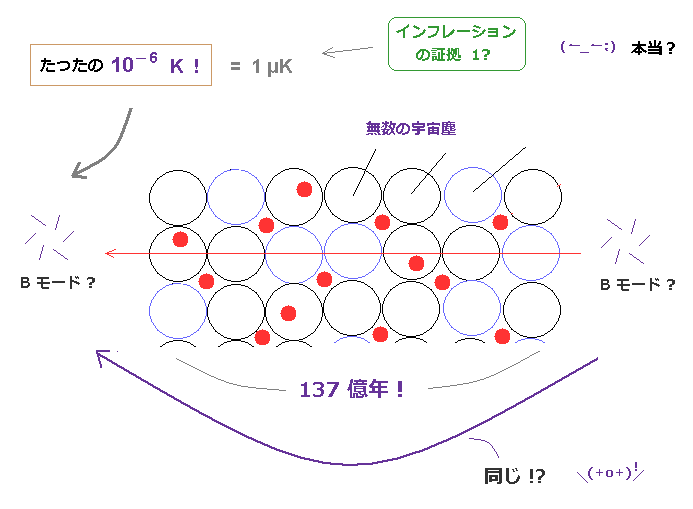
このサイト や このページにあるように、B モード偏光の電磁波は あまりにも弱い (= たったの 0.4 μK しかない )。
常識的に考えれば、 このかすかすぎるマイクロ波が 137 億年もの大昔のインフレーションの跡がそのまま残ったものであろうはずがない。
現在の宇宙論は 一様すぎる宇宙マイクロ波背景放射 (= CMB, 3 K ) と かすかな B モード偏光 (= 0.4 μK ) が 膨張宇宙の結果であるという 歪曲された解釈に頼らざるを得ないのである。
なぜなら 相対論的に 宇宙空間の一様なエーテル様物質の存在を否定してしまったからである。
( じゃあダークマターやダークエネルギーは 何なのかという話になる。)
これほど微弱な B モード偏光のパターンが 137 億年もの気の遠くなるような期間中に 放出された大量の放射線や、宇宙塵などの影響を掻い潜って 現在まで その姿を保てるわけがないことは 誰が見ても明らかである。
(Fig.3) 致命的なパラドックスを無視 → インフレーション、超対称性などの "ファンタジー"理論の温床。
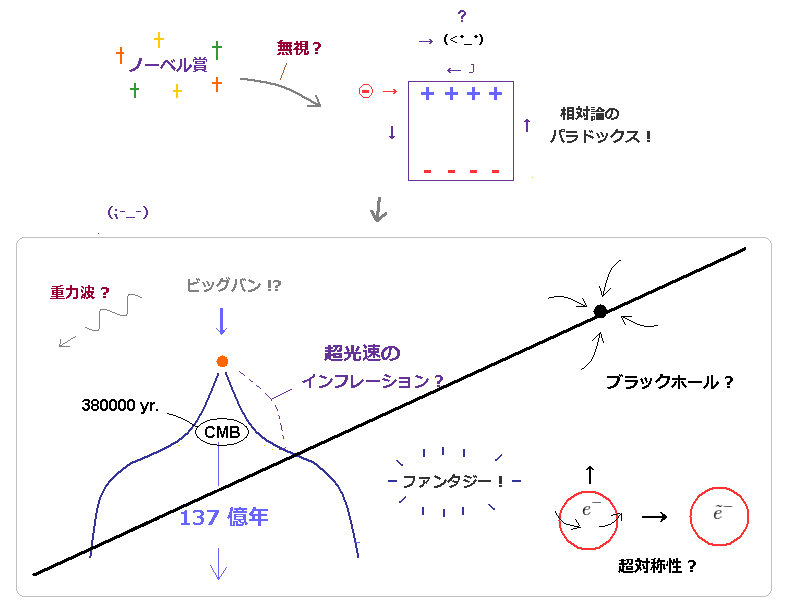
このページ や このページにあるように、特殊相対論は ローレンツ力や 直角レバーの例にあるように、 致命的なパラドックスを抱えている。
じゃあ なぜ皆さんが知らないのかというと、恐ろしいことに ほぼすべての相対論関係の教科書、大学の先生、メディアなどが これらの存在を ひた隠しにしているからである。
もちろん、事実をひた隠した代償は大きい。
新しい学生や 一般人が 騙されて相対論関係の理論の方にすすめば、貴重な人生が台無しになってしまうからである。
10 次元の超弦理論、超対称性、素粒子理論 ( ヒッグス )、インフレーション、 重力波などの理論は すべて 相対性理論が正しいという前提条件のもとに作られた理論である。
つまり、特殊相対論が 致命的なパラドックスを含んでいたら、これらの理論は すべて間違いということになる。
たちが悪いことに、これらの理論に関連して 今まで 多くのノーベル賞が与えられてしまったことである。
世界で一番 影響力のある賞が 間違った理論に与えられたときのその副作用は あまり想像したくないくらい甚大である。
(Fig.4) 一般人からの "重税" を元に 高価な加速器建設。 → 何の恩恵もなし ( メディアを除き )。
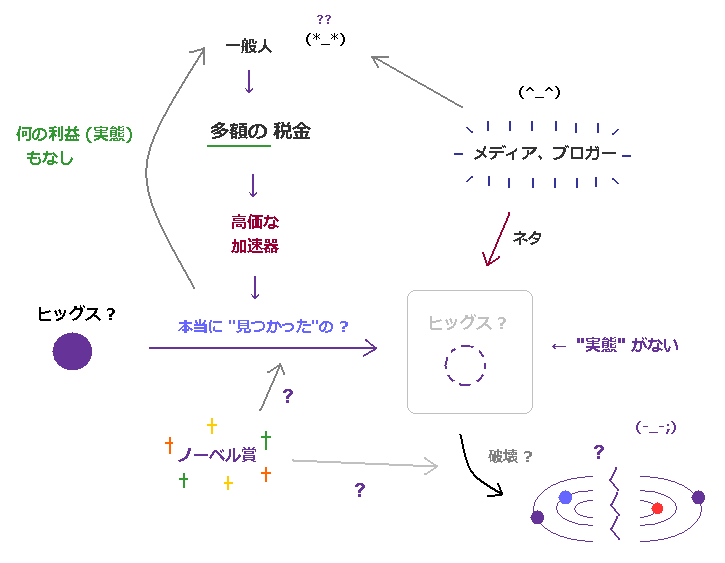
ヒッグス粒子が発見されたというセンセーショナルなニュースが 一斉に流れてから かれこれ数年経つが、実際ヒッグス粒子によって 日常生活が変わったなどの話は とんと聞かないであろう。
残念ながら、 ヒッグス粒子とは この程度の"実態のない"存在なのである。
一般人の多額の税金を元に建設された 高価な加速器によって 発見されたとされるヒッグスは メディアやブロガーが取り上げる ニュースや"ネタ" として生き残っている "架空"の粒子なのである。
それにも関わらず なお 日本などに新型の加速器を 多額の税金を使って 建設しようとしていることは 余りにも無責任な話である。
例えば、ノーベル賞がヒッグス粒子に与えられたために、その影響で 様々な 突拍子もない ヒッグス関連のニュース ( 例えば ヒッグス粒子によって宇宙が崩壊 !? このサイト や このサイト 参照 ) が飛び交うことになってしまった。
例え ヒッグス粒子が 2つ もしくは 何個見つかろうが、何の実態も利益もなく、メディアやブロガーの格好のネタとなるから 騒いでいるだけの状況は 即刻 改めなければならない。
(Fig.5) ヒッグスは あまりにも低頻度 (= 1/1000000000000 ) で リアリティーなし。

このサイト や このサイト にあるように、 1 兆回以上の陽子を衝突させて ようやく 1個のヒッグス粒子ができるぐらい その生成率は 低い。
それはまさに 干し草の中から 針を見つけるかのよう と例えられるぐらいである。
さらに このサイトにあるように、ヒッグス粒子の寿命は たったの 10-22 秒 しかないらしい。余りにも不安定である。
標準模型は ヒッグス粒子は 私達の周囲一面に分布しており、 すべての物に質量を与えていると主張している。
しかし 加速器内で生成されたとされる 非常に稀で かつ不安定なヒッグスが 本当だとすると、それは "安定的に" あらゆる物に質量を与えることができないことになる。
それに もし私達の周囲に "無数"のヒッグス粒子が存在するとしたら、 金食い虫の加速器内だけでなく 日常生活において 簡単に ヒッグス崩壊を検出できるはずである。
(Fig.6) どうして 高価な加速器が必要なのか ← 意味がない。
無数のヒッグスが いたるところに存在して すぐに崩壊するのなら、どこかしこで 高価な加速器に頼らずとも、容易にヒッグス崩壊を検出できるはずである。
それができないということは LHC で発見されたというヒッグスは 元の無数のヒッグスという定義と まったく別物ということになる。
β崩壊は 稀な現象ではなく、その過程で 重い W ボソン (= 陽子の 80 倍 も重い! ) が生成されることになっている。
この W ボソンが生成されるとき、その場に ヒッグスが存在しないと、W ボソンに質量を与えることができない。
つまり、この通常のベータ崩壊の過程で、不安定な W ボソンと ヒッグス粒子の両方の崩壊を 通常の環境下 ( 加速器なしで ) で 容易に検出できることになる。
しかし 実際には β崩壊時にこれらを検出することは 不可能である。
要するに 加速器内で生成崩壊検出したとされる W ボソン や ヒッグス粒子というのは 標準模型が主張する β崩壊や 無数のヒッグスという定義と 完全に矛盾した別物ということになる。
(Fig.7) 現在の物性物理は "架空の" 準粒子を作ることで止まってしまっている。

現在の物性物理学は 1920 〜 1960 年代の 非常に 古い時代に 定式化されたものであるため、当然 現在のコンピューターの使用などを想定した理論ではない。
この極度に制限された状況でも 当時の物理学者達は より良いポストを求めて 彼らの研究を続けなければならなかった。
結果的に、多体効果を扱えない代償として 架空の 準粒子を 作らざるを得なかった。
例えば、 フォノンとは 原子の格子振動を 別名で言い換えただけで、もちろん 本当の 粒子ではない。
これが "準粒子" と呼ばれる理由である。
BCS理論における
ボゴリューボフ準粒子 (= γ† ) は 電子の生成因子と消滅因子の組み合わせで定義される。
つまり 通常の粒子の生成因子の定義と 完全に矛盾した存在であることが分かる。
(Fig.8) つまり 今から 2000 年後も 準粒子は "仮想の" 数式記号のままである。

もちろん、本当の"科学"においては、目の前に分からないことがあれば、"真実"の追及を
継続しなければならない。
つまり 架空の準粒子は すみやかに 本当の粒子を用いて 説明されなければならない。
ところが驚いたことに、現在の量子力学は この科学的精神に逆行して、"意図的"に これら架空の準粒子の種類を増やそうとしているのである ( リスト参照のこと )。
さらに困ったことに 彼らは これら架空の準粒子が何なのか 永遠に問おうとしないことである。
このような 非常に矛盾した量子力学に固執する限り、準粒子は 今から2000 年後も"架空の" 粒子のままということになる。
また 非常に抽象的な 数式記号 (= 生成消滅演算子 ) には 各粒子の 具体的かつ ダイナミックな動きを表現できる能力は まったく ない。
(Fig.9) 質量のある電子が 突然 質量ゼロ !? 分数電荷 エニオン は ファンタジー。

このページに示したように、現在の物理は 質量のある電子を用いて 質量ゼロのディラック粒子を こしらえようとしている。
これは ある1つの実験装置 (= ARPES ) の曖昧な結果から 強引に導いているだけ ( 結果の解釈が強引 ) で、この粒子にリアリティーは何もない。
また、整数量子ホール効果を "仮想の" ベリー位相や モノポールをこしらえて 説明しようとしている。
また このサイト や このサイト にあるように、分数量子ホール効果 を説明するために 何と 分数電荷の エニオン という奇妙な準粒子を導入した。
もし ノーベル賞が これら 架空の準粒子に与えられたとしたら、当然 お墨付きを得た 準粒子は 架空のままで 真理の追求は 大幅に遅れることになる。
(Fig.10) "ファンタジー"の量子力学は 本当のミクロ世界の解明を 阻害している。
量子力学は 1920 年に導入されて以来、超光速の スピン や 多世界 (= シュレディンガーの猫 ) など 余りにも現実離れしていたため 様々な批判を招いた。
基本的に 量子力学は 非常に 曖昧な態度 をとり続け、ミクロの世界を明らかにすることを 意図的に避ける ことによって、生き残ってきたといっていい。
曖昧な波動関数が 多体粒子の具体的な ダイナミックな 動きを表現することが できなかったために、 仮想の準粒子 や 量子コンピューター (= わずか ナノ秒で壊れて非実用的 ) という 仮想の目標をこしらえて アピールしてきた節がある。
人間も含めた 地球上の生物の体は ミクロな微生物ですら 非常に高性能な ナノマシーンであり、今だに 私達の知識で 全然解明できていない部分が多い。
ミクロの世界を明らかにすることから逃げていれば、応用分野 ( 医療など ) で、がん、HIV、ALS、重度のアレルギー、認知症 などの 深刻な病気を 根本的に治療することが 永遠に "できない" ということになる。
(Fig.11) 超光速の量子もつれの本当のメカニズムは? → 永遠に "だんまり" ?
このページにあるように、非常に長年の研究にも関わらず、超伝導量子ビット (= 量子コンピューター !? ) のコヒーレント (= 作動 ) 時間は たったの ナノ秒 〜 μ秒 ほどしかない。
つまり 同じような論理に基づいているかぎり、実用的な量子コンピューターなど できるはずがないのである。
超光速の 量子もつれ のトリックは 仮想の "光子" という粒子の前提条件にあることは明白である。
現在の研究者達は 事あるごとに この便利な "量子もつれ" という ワードを使いたがる傾向にある。
しかし 超光速のリンクは 非常に小さな固体、量子ビット ( 〜μm ) では、証明できていないし、できない。
非常に長きにわたる研究期間にも関わらず、量子コンピューターが まったく 実現されていない 事実を見れば、便利な 量子もつれ や 量子コンピューター という語は 量子力学そのものの無用性を 覆い隠すために 悪用、多用されていることは 一目瞭然である。
もし ノーベル賞が この ( 超光速 ? ) の "量子もつれ" に与えられれば、真のメカニズムの解明は 大幅に 阻害されることになる。
(Fig.12) 光子が電子から放出 → その時の加速度が "無限大" !
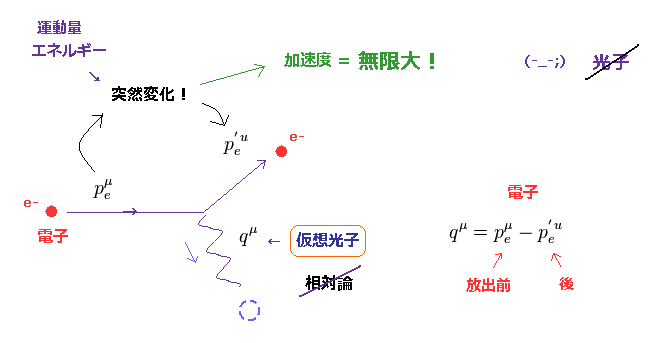
このページにあるように、光子というのは 単なる抽象的な記号にすぎず、 物理的実態がない ( 形や大きさなど )。
こんな曖昧な光子( 関連 ) の研究 ( 例えば "量子情報" ) に ノーベル賞 がお墨付きを与えてしまったら、電磁場の 本当の姿、性質の解明は また先延ばしとなってしまう。
基本的に 場の量子論によれば、光子の現象は ファインマンダイアグラム によって記述されることになる。
驚くことに、放射 ( もしくは吸収 ) された光子と 電子が エネルギー・運動量保存という基本的な法則を満足するとき、この光子は 必ず仮想光子 というものになる。
このページ や このサイト にあるように、この仮想光子は "タキオン" のように 特殊相対論に 従わない。これが "仮想" と呼ばれる所以である。この時点で この理論は終わっているのだが。
さらに 光子が 電子から放出 ( もしくは 吸収 ) されるとき、この電子の運動量とエネルギーは 突然変化する。
これはつまり、この時点での電子の加速度は 無限大 ということになり、あり得ない現象であることが分かる。
私達は この変化の様子を その場、ドブロイ波全体も含めた ダイナミックで具体的かつ現実的なモデルで置き換える必要がある。
(Fig.13) 光子のスピン = ( 左右 ) 円偏光 ? では 直線偏光は?
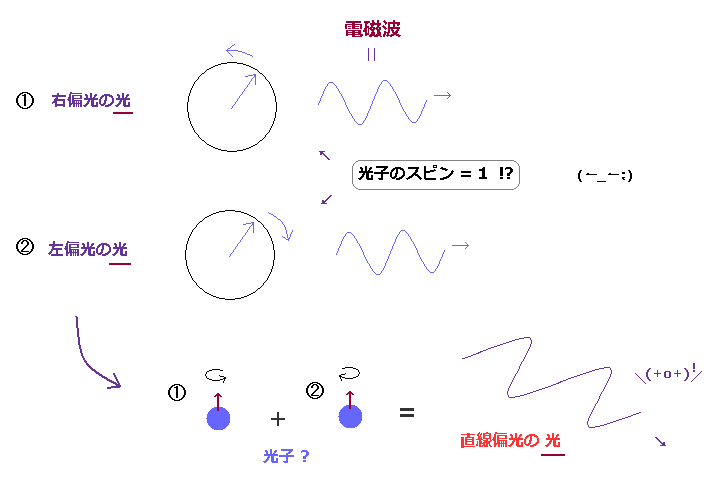
このサイトにあるように、 電磁波が 円形に 偏光しているとき、その方向を 単に "スピン" と呼んでいるにすぎない。
つまり 光子のスピンとは 単に 古典的な 光の偏光方向を指しているだけで、非現実的なスピンとは 何の関係もないのである。
それでは、通常の 直線偏光の光には スピンがないということか?
このサイトにあるように、左右の円偏光の電磁波が 同じ割合で混合したときを 直線偏光と定義している。
ご覧のとおり、光子のスピンとは 非常に 都合よく作られた 実態のない概念であることが分かる。
実際、 この論文では、 偏光した光 (= "polarized lights" ) という用語が 頻繁に 見られる。
(Fig.14) 誰が "スピン" を必要としているのか?
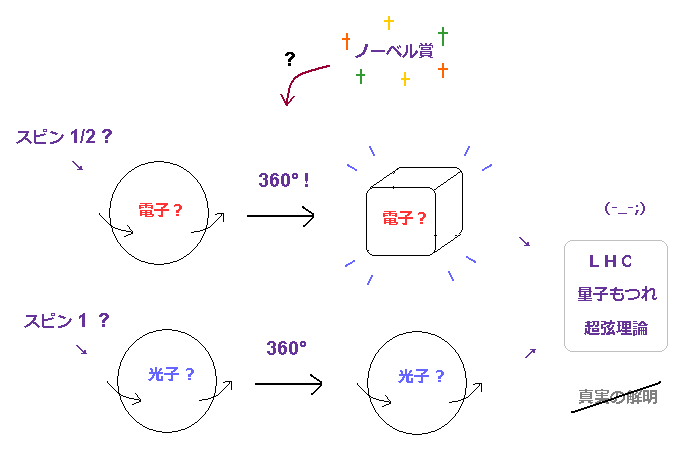
このページに述べたように、電子のスピン 1/2 は 何と 一回転 (= 360°) で 元に戻れないのである。非常に非現実的な概念である。
一方で、光子のスピン1は 一回転で戻れるから リアルかと言えば、そんなことは全然ない。
光子のスピンは 単なる電磁波の偏光状態を 言い換えただけであり、なぜ 彼らは "スピン" という語を 何でもかんでも つけたがるのだろうか?
なぜなら 現在の量子力学は この 架空の "スピン" というものに 完全に拘束されていて、このことが より深い真理の解明を 阻んでいると言える。
例えば、光子 ( 相対論に反する仮想光子も含めて ) や スピン が存在しなければ、現在の標準模型は 根底から 崩れることになる。
現実的に ヒッグス や 超対称性 という語が メディア ( ex. Scientific american ) や ブロガー達の 単なる 格好のニュースアイテム としてのみ姿を表す状況をみれば、この "スピン" が非実在 (= 別物で置き換える ) であるとしても 私達の生活に何の影響も与えないことが分かる。
さらに このページに示したように 光子という粒子を示す 直接的な 実験証拠は まったくない。
この架空の光子は 素粒子物理学、量子もつれ (= 量子コンピューター、量子情報 )、10 次元の 超弦理論 にとって、必須のため 抽象的な概念として 残っているにすぎない。
(Fig.15) スピン・スピン相互作用は たったの 10-6 eV、 これは 0.05 K で壊れてしまう。
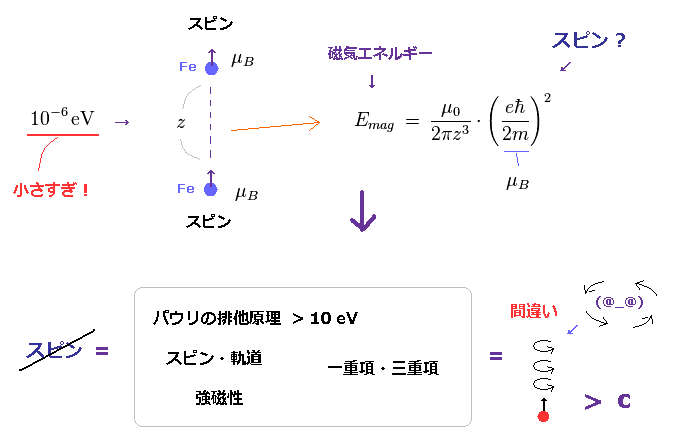
このページ や このサイト (p.7) にあるように、スピン・スピン磁気 (= ボーア磁子 ) 相互作用は 弱すぎて ( 0.05 K 温度換算で ) 実際の強磁性 ( 鉄は 1043 K まで強磁性を保持できる ) をまったく説明できない。
例えば、 Fe-Fe 間の平均的な距離は 約 2.8 Å (= 2.8 × 10-10 meter ) である。 このサイト (p.2) など。
このページ、 このサイト、 このサイト (p.6) などを用いれば、スピン・スピン磁気双極子作用というのが あまりにも 弱すぎることが分かる。 たったの 4.55 × 10-6 eV (= 0.05 K ) ほどである 。
パウリの排他原理も この弱すぎるスピン・スピン相互作用では まったく説明することが できない。
このサイトにあるように、 リチウムの3つの電子がすべて 1s 状態にあるとすると、そのエネルギー
(= 8.46 = -230 eV ) は 実験値 (= -203 eV ) よりも 低くなってしまう。
この大きなエネルギー差 ( 27 eV = 230 - 203 eV ) は パウリの排他原理の反発力が ドブロイ波の干渉などの 他の強力な効果によることを示している。
さらに、ナトリウムの D 線 の分裂幅も スピン軌道相互作用で 説明するには 余りにも弱すぎる。
もしノーベル賞が これら 実験値と根本的に異なる概念 (= スピン ) に与えられれば、量子力学の "問わない" 姿勢が継続されて またもや 真理の解明は 遅れることになる。
(Fig.16) 波動関数の収縮 = 多世界 もしくは "超光速" !?

量子力学の シュレディンガー方程式は "曖昧な" 確率密度を提示することしかできない。
つまり その電子を観測しようとした瞬間に、様々な状態で成り立った
"重ね合わせ" 状態が 1つの電子に 収縮することになる (= 波束の収縮 )。
この波束の収縮の速度は 一瞬なので 超光速である。
この考えが 量子もつれの "源泉" になっている。
標準的な コペンハーゲン解釈では、観測者は 波束の収縮を引き起こす "特殊能力" を持っている。
そのため この解釈は 非常に 不自然と言える。
そのため 非現実的な 多世界解釈が 導入され、現在の量子力学の解釈において 支配的な立場にある。
多世界解釈では、観測者が 電子を観測しようとするとき、彼は 多数の状態 (= 世界 ) のうち 1つの世界 を見るということになり、その収縮速度は 光速 "c" を
超えないということになる。
もちろん、この 多世界解釈 は 非常に強引で "あり得ない" 解釈であることは明白である。
しかし 量子力学では 電子を リアルな 粒子、波で表現することが 不可能なので 消去法で残っているという始末である。 (= ボーム解釈など。 )
(Fig.17) 角運動量 = 0 → 電子が 原子核に "衝突" ? 波がキャンセルされる ?

水素原子のシュレディンガー方程式の解にあるように、量子力学は 角運動量 0 という 非現実的な状態を 常に必要としている。
この状態では 電子は 常に原子核に 衝突したり、それを貫いたりしているということだろうか? あり得ない話である。
すべての波動関数は ドブロイの関係式をベースにしている。
しかし このゼロの角運動量が本当だとすると、電子が線状運動することによって、自身の波で 打ち消し合ってしまうことになる。
つまり、リアルな 電子、波 という考え方が 量子力学では
不可能であることが分かる。
これが ガイド波理論 (= ボーム解釈 ) が 受け入れられてない理由である。
(Fig.18) シュレーディンガーの 2P の"動径" 波動関数 ( 角運動量 = 1 ).
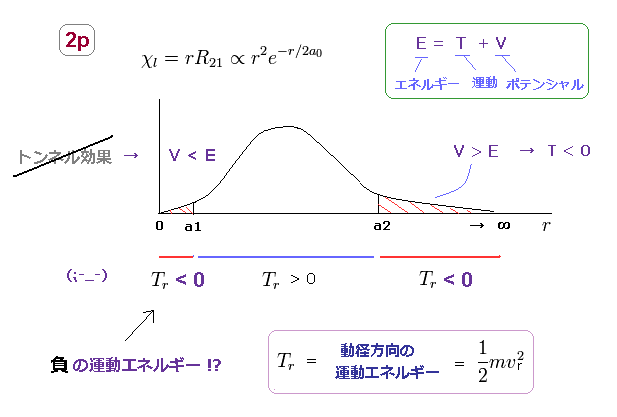
例えば、シュレーディンガーの 2P の状態では、Fig.18 に示すように 動径方向の運動エネルギー ( Tr = 1/2mv2 ) が 両サイドで マイナスになる。
a2 < r の領域では、ポテンシャルエネルギー V は 全エネルギー E よりも 高くなる。
結果的に 運動エネルギーは 負になってしまう ( ← あり得ない話である )。
r < a1 の領域では 今度は 接線方向の運動エネルギー (= Tt ) が 非現実的なくらい大きくなる。
この増加を キャンセルするために、動径方向の運動エネルギー (= Tr ) は 負 にならなければならない ( ← これは V < E のため トンネル効果とは 全然違う。)
つまり シュレーディンガーのモデルは 完全に非現実的な概念に立脚したもので 明らかに 間違いである。( このページも参照のこと。 )
この非現実的な領域も リアルな電子の解釈 (= ボーム解釈 ) を不可能にしている原因の1つである。
(Fig.19) 教科書の ボーア模型に関する説明は 間違い。
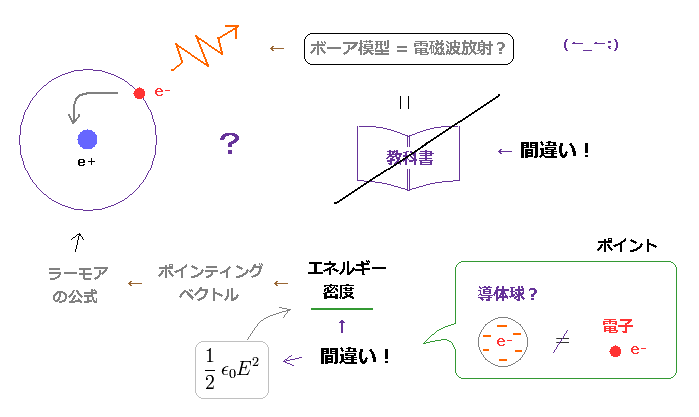
通常の教科書は 古典的なボーア軌道の 加速する電子 は エネルギー放射して 核に落ちて行くと くどいくらいに 述べている。
残念ながら これらの説明は 完全に誤りであり、一般の多くの人達が 通常の教科書や ウェブサイトによって 誤った考えを 安易に吹き込まれていると言える。このページも参照のこと。
この主張は ポインティングベクトル (= E × H ) を エネルギーの流れとして用いている。
この ポインティングベクトルは 真空における 電場、磁場のエネルギーの変化を表している。 このサイトも参照のこと。
この真空における電場エネルギー (= 1/2εE2 ) は 中心の 導体球 に マイナスもしくはプラスの微小電荷を 集めるのに必要な ポテンシャルエネルギーを意味している
(= Fig.20 左、 このサイトも参照のこと )。
(Fig.20) ボーア模型の加速する単一電子が電磁波放射? ← 一種のマインドコンロトール。
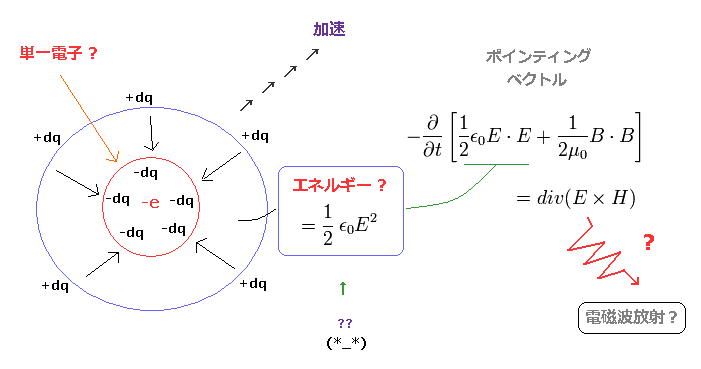
しかし 単一電子は それより 小さな電荷の集まりではない ( 単一電子は 最小の電荷である )。
これはつまり 真空の電場エネルギーというのは 単一電子においては エネルギーを 意味していないことになる。
すなわち ポインティングベクトルは 単一電子の場合は エネルギーの流れではないため、単なる円運動だけで エネルギーを失うことはないということになる。
この当たり前のように教科書で見かける間違った説明は ボーア模型に対する 一種のマインドコントロールとして作用していると言える。 困ったものである。
2つ以上の電荷が 関わっているときのみ、電磁波放射が可能と言える。
(Fig.21) ヘリウムは 2つの水素原子が 重なっただけのものではない。
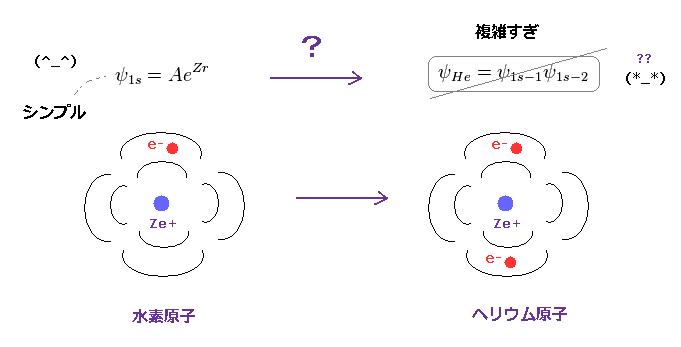
量子力学の ほとんどの教科書は 水素原子の波動関数のみ 扱っている。
しかし 複数電子の原子系を扱えなければ、実際の科学の現場では まったく役に立たない。
実は、単純なヘリウム原子でさえ 解析的に 解くことができない。
ヘリウムは 3体問題であり、その波動関数 (← 決まらない ) は 非現実的なくらい
複雑である。
ヘリウムの2つの電子は 互いに 避け合っている。
この複雑な運動のため、ヘリウムの波動関数は 単純に2つの水素原子を合わせればいいと言う訳にはいかない。
(Fig.22) 2つの電子間の反発が 波動関数を 扱いにくくしている。
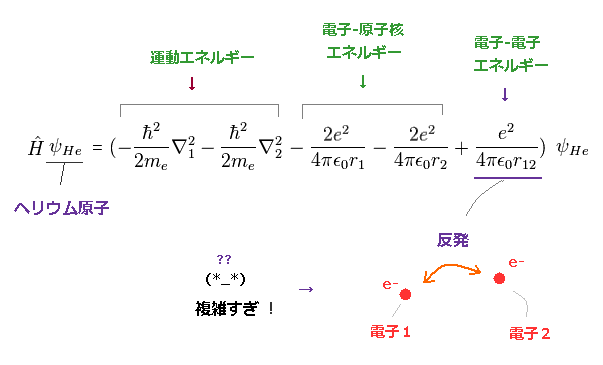
ヘリウムのシュレディンガー方程式は 3つの部分: 運動エネルギー、位置エネルギー、2つの電子間の反発エネルギー、から成る。
(Fig.23) 2つの電子間の距離。

ここでは r12 は 2つの電子間の距離である。
この変数の存在が ヘリウムの式を 非常に複雑にしている要因である。
(Fig.24) ヘリウム = 水素原子 1s + 水素原子 1s ?
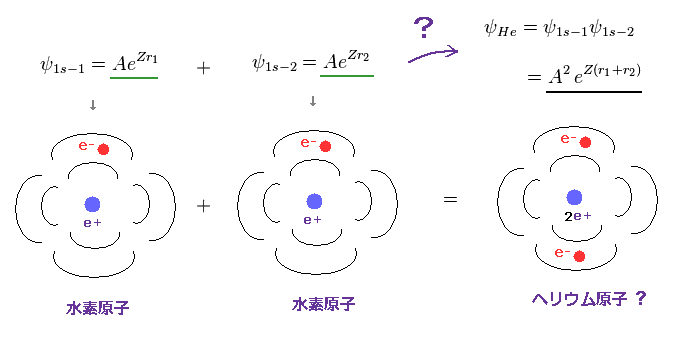
量子力学では ヘリウム原子の2つの電子とも 1s 状態 ( 角運動量が ゼロ ! ) にあることになっている。
最初に、ヘリウムの波動関数が 2つの 1s の水素原子の波動関数でできているとする
( 2 × ψ = A eZr ).
ここで 指数関数部のパラメーター (= "Z" ) は 有効電荷 を表す変分パラメーターである ( 水素では Z = 1 )。
Fig.24 を Fig.22 に代入すると、
(Fig.25) 計算結果 (= -77.49 eV ) は 基底状態のエネルギーより 高い。

このサイト や このページにあるように、 全エネルギー E を最低にするように、パラメーター Z を変分法によって変化させて 計算値 -77.49 eV の値を得ることができる。
この値は 実験値の基底状態エネルギー (= -79.005 eV ) よりも 高い。
なぜなら Fig.24 の波動関数は 2つの電子間の 反発運動を 考慮していないからである。
(Fig.26) ヘリウム原子の 有効電荷は 1.6875 ?
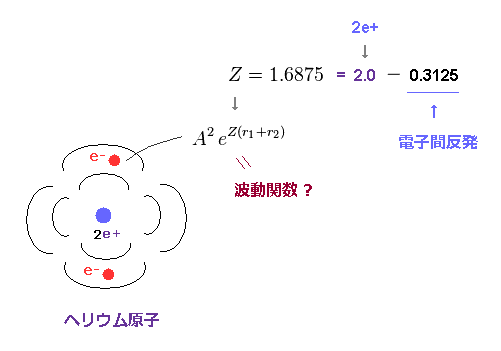
Fig.25 に示したように、有効電荷 Z が 1.6875 のとき、全エネルギー E は 最も低くなる。
2.0 (= ヘリウム原子核電荷 ) と 1.6875 の 差 (= 0.3125 ) は 他の電子との 反発効果による影響である。
(Fig.27) 2つの電子は "実際に" 避け合っている。
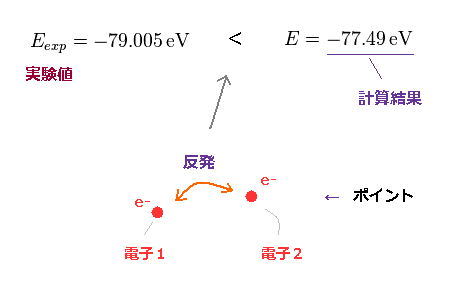
この結果に見られるように、ヘリウムの2つの電子は 現実的に 互いに 反発し 避け合っており、この エネルギー差につながったことが分かる。
(Fig.28) 2つの"広がった"確率密度波が 互いに避け合えるの?
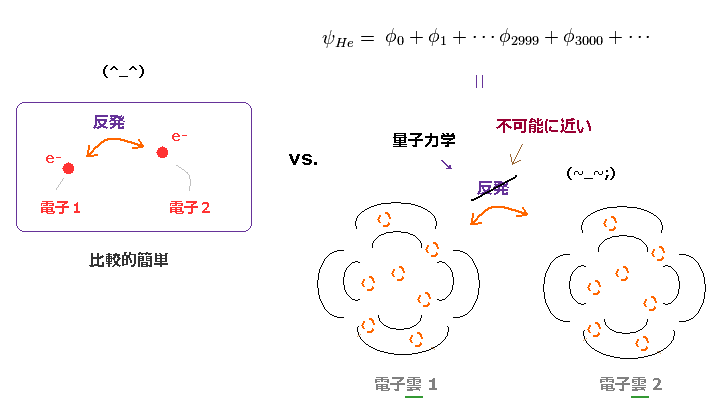
量子力学によれば、シュレディンガーの波動関数は 全空間に広がった "確率密度波" を意味している。
通常の電磁気学と 異なり、これら 空間中に広がった電子同士が 互いに避け合うのを表現することは 非現実的なくらい難しい。
そのため 単純なヘリウム原子でさえ、量子力学的計算では3000 以上もの "複雑な" 項 を必要とする (← 非実用的である ) 。 この論文など参照のこと。
(Fig.29) あらゆる種類の変分関数を試して 真のエネルギー値を知ることは不可能。

Fig.24 に示したように、シュレディンガーの波動関数は 電子間の反発効果を 考慮していない。
そのため 計算結果のエネルギーは 必ず 真の基底状態よりも 高くなる。
このエネルギーを下げるために 変分法と ヒレラス (= Hylleraas ) 関数や 配置間相互作用 (= CI ) などの 複雑な関数を使用する。
すでに述べたように、これらの波動関数は 単純なヘリウム原子ですら 3000 以上にもわたる 項 が必要になってくる。あまりにも 非現実的である。
この変分法によって 正確な基底状態のエネルギーが得られると言われているが、この解釈は 非常に 疑わしい。
なぜなら そもそも すべての種類の変分関数を試すことが 不可能だからである。
つまり すべての関数を試して、一番低い計算値を知ること自体が不可能ということである。
実際に この論文 (p.3)では 正確な値を得るのに 変分でなく k = 2.0 という値に固定して計算している。
基本的に 指数関数パラメーターの数を増やして それぞれを独立に変化させれば、より低いエネルギー値を得ることができるが この論文では 1つのパラメーターのみである。
また この論文では、この指数パラメーターを 変分法でなく、別の方法で選んで 正確な値を出したとしている。非常に奇妙としか言いようがない。
(Fig.29') ヘリウムの波動関数は あらゆる地点で エネルギー保存則を満たさない。
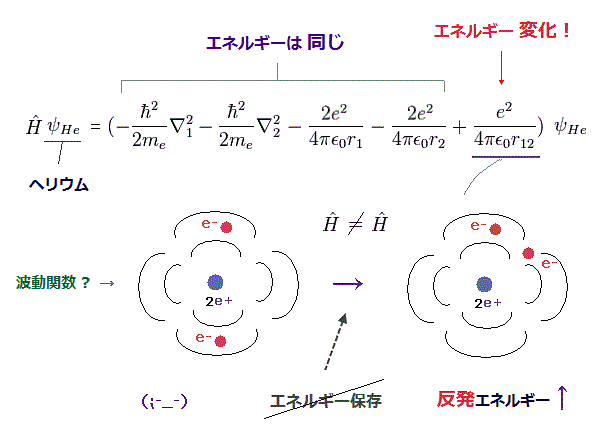
ヘリウム原子は 2つの電子を含んでいるため、その式を解くことは できない。
そのため、最初に 何らかの近似的な 波動関数を選択することから始めなければならない。
重要な点は 量子力学においては 定常な波動関数を使用すると、水素原子を除き すべての原子、分子において エネルギー保存則という基本原理を満足していないことである。
定常な波動関数では、運動エネルギーと 各電子と原子核間のポテンシャルエネルギーは 決まった定常値になる。 しかし 2電子間の反発エネルギーの部分は 電子間距離 (= r12 ) に応じて 変化してしまう。
すなわち、電子間距離が ゼロ に近づいた時は、ポテンシャルエネルギーが 無限大まで 増大してしまうことになる。
2電子の位置関係に応じて ヘリウムの全エネルギーが 変わってしまうということは エネルギー保存則という基本原理が破れていることを意味している。
解くことができる水素原子においては、当然 電子の全地点において 全エネルギーは保存され 定数になる。
要するに 波動関数に基づく量子力学は 多電子原子を扱えないことになる。
この模型のみ 特定の軌道上のすべての地点で エネルギー保存則が 満たされる ことになる。
(Fig.30) 複雑なシュレディンガー方程式 + 行列式は 分子などで 使い物にならない。
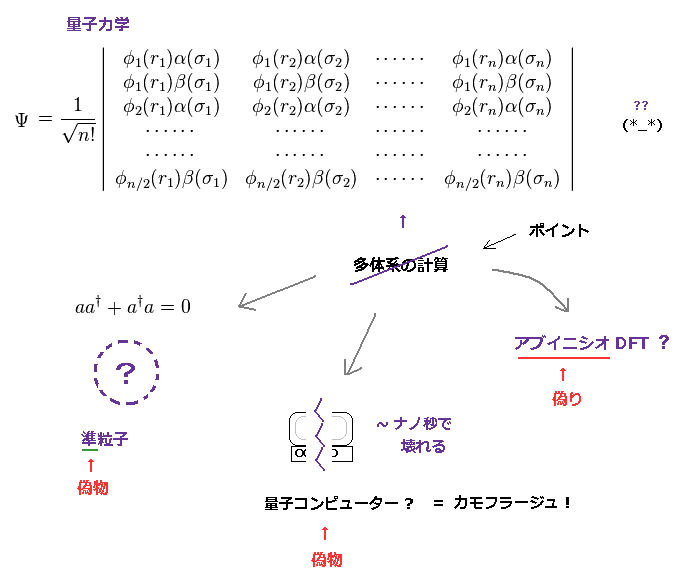
例えば、単純なヘリウム原子でさえ 電子が 互いに避け合うのに 量子力学では 3000 項以上もの項 ( ← 非現実的 ) を必要とする。 このサイト参照のこと。
つまり 現在の量子力学では 大きな分子などを 扱うこと自体が不可能なのである。
次の 非常に興味深い論文 には こう書いてある。
----------------------------------------
p.5. "第一原理" という語を 密度汎関数法 ( DFT )
の研究者が 好んで使用したがるが、この方法が
準経験的 (= 第一原理でない ) な要素を含んでいることは明白である。
p.6. 現在の アブ・イニシオ計算に関して言えば 実は色んな 実験値のパラメーターに依存しており、アブ・イニシオ (= 第一原理 ) とは呼べない。
------------------------------------------
これら 架空の準粒子、"偽の" アブイニシオ DFT、カモフラージュの量子コンピューターは すべて 量子力学の不都合な真実を 隠すために導入されたと言っていい。
(Eq.1) 密度汎関数法は 第一原理ではない。
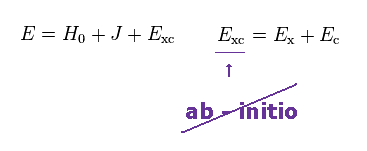
密度汎関数法では 電子間相互作用などを表す
交換相関汎関数の部分が まったく未定であり、 私達の都合に合わせて 自由に変えることが可能である。
つまり この分野の物理学者達が 好んで "アブイニジオ (= 第一原理 ) DFT 計算" という語句を使用したがる傾向と裏腹に、DFT 自体 まったく アブイニジオ計算では ないのである。
このサイトや このサイトが指摘するように、本来は無理なのに、第一原理と呼びたがる傾向が強かったために 歪曲された名称がついたと言っていい。
(Eq.2) LDA - VWN 相関汎関数。

このサイト p.4に、LDA の相関エネルギーの表現には いくつか候補があり、モンテカルロシミュレーションなどの計算結果などに パラメーターをフィットさせて得られると書いてある。
LDA の もっともポピュラーな 相関汎関数が Eq.2 に示したVWN-LDA である。.
Eq.17 の ε は このサイト (p.9) にある。
この LDA の相関汎関数は 12 もの フィッティングパラメーターを含んでいる。
つまり まったく第一原理ではないのである。
(Fig.31) 異なった電荷 Z を持つ 2つの H の波動関数の重ね合わせ。
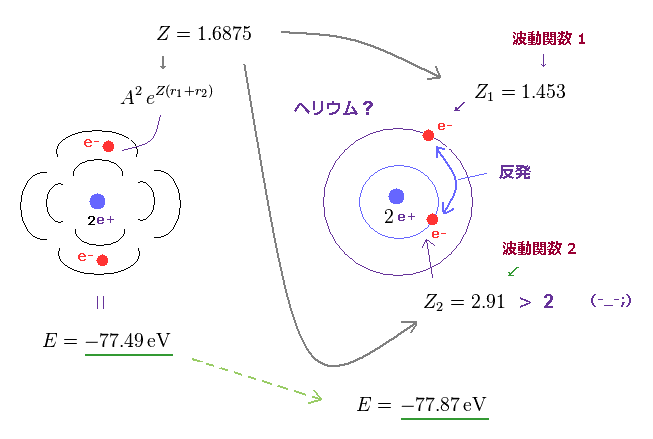
すでに述べたように "広がった"波動関数を用いて 2つの互いに避け合う電子を説明することは 非常に 難しい。
方法の1つに 配置間相互作用法
(= CI ) がある。
Fig.31 にあるように、ヘリウム原子が 異なった 有効電荷 Z ( ex. Z1 =1.453, と Z2 = 2.91 ) を持つとき、これら2つの波動関数は 互いに わずかに避け合うことができる。
(Fig.32) "重ね合わせ状態" で 2つの電子が 互いに避け合える?

このサイトを用いると 様々な Z を入力して ヘリウムのエネルギーを計算することができる。
2つの有効電荷 Z が 1.45 と 2.90 のとき、計算値は 最も低くなる (= -77.87 eV ).
もちろん、この値は 真の値 (= -79.005 eV ) には まだまだ届いていないため、ここに 膨大な項 ( ~ 3000 以上 ) を付け足して、強引に実験値に持っていくわけである。
お気づきのとおり、電荷 Z = 2.91 というのはあり得ない状況である。それは ヘリウムの核の電荷 Z = 2 を 越えているからである。
つまり ヘリウムの波動関数は "非実在" の部分を含んでおり、 物理的意味を 何も持ち合わせていないことになる。
このページ (p.4251) に次のようにある。
-------------------------------------------
エネルギーの最も低いときは k の値が Z よりも大きくなる。
つまり このパラメーターが "有効核電荷" であるという解釈は まったく成り立たない。
-----------------------------------------
(Fig.33) 2つの電子間のクーロン反発作用が 小さくなる?

Fig.33 を見て分かるように、この波動関数の重ね合わせ状態は 電子間反発相互作用を 弱くしている。
なぜなら これら2つの Z のパラメーターが 異なるため、2つの波動関数の重なり部分が 小さくなったからである。
(Fig.34) 波動関数が収縮 (= Z が大きく ) すると、ポテンシャルエネルギーは どう変化する?
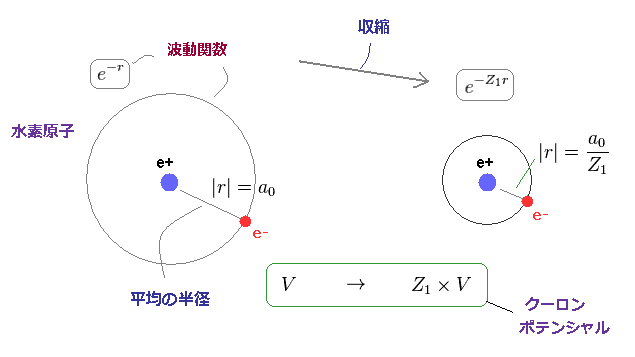
しかし この "重ね合わせ" の波動関数は 現実的な視点から見て、 理不尽であり得ないことが分かる。
Fig.34 にあるように、有効電荷 Z が大きく ( 1 → Z1 ) なると、この波動関数は 収縮する。
すると 平均の半径は × 1/Z1 に比例して短くなる。
その比率で ポテンシャルエネルギー (= V ) も 低くなる。
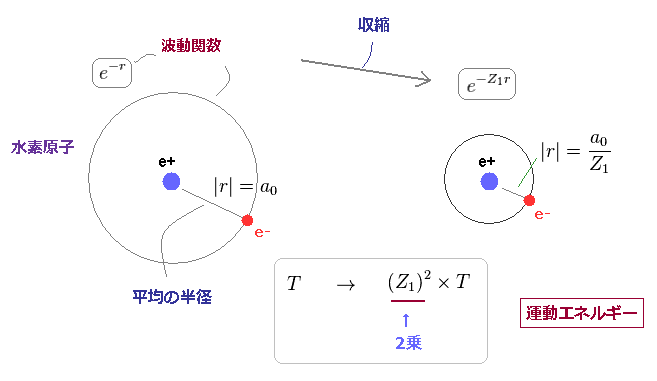
(Fig.35) 運動エネルギーは 増加しすぎる。

電子の運動エネルギーに関する情報は 波動関数に含まれている。
Fig.35 を見て分かるように、この運動エネルギーは Z1 の
2乗に伴って 大きく なりすぎてしまう。
(Fig.36) 波動関数が収縮 → 運動エネルギー (= T ) が Z2 に比例して増加。
このページにあるように、これが 変分法の メカニズムであり、 ビリアル定理を満たす平衡地点が 最も 低いエネルギーとなる。
(Fig.37) 全エネルギーが 上がりすぎる ( 1/2 V → ゼロ !? ).
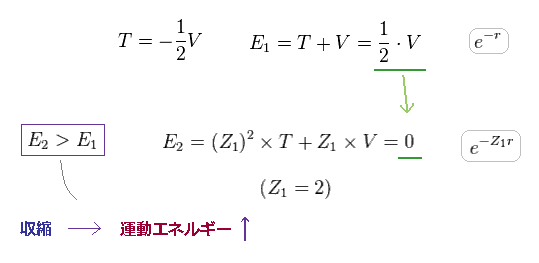
ここで Z = 1 のとき この波動関数が ビリアル定理 ( T = -1/2V ) を満たすと仮定する。
Fig.34 と Fig.36 から、全エネルギー E2 は 元の E1 よりも はるかに高くなることが分かる。
例えば、波動関数が 1 → Z1 = 2 に従って収縮すると、全エネルギーは ゼロ まで上がる (← 負ではないので あり得ない状況である )。
つまり、指数パラメーター Z を変えていくという考えは 本当の電子の動きと
矛盾しているのである。
なぜなら この重ね合わせの波動関数は
異なった Z 間で エネルギー保存則を満足していないからである。
(Fig.38) r12 = 2つの電子間の距離。

2つの互いに避け合う電子を表現するのに 別の方法がある。
ヒレラスの施行関数は 2つの電子間の距離 (= r12 ) の変数を含んでいる。
この方法は 計算が 非常に難解であるため、ヘリウム、リチウムなどの 非常に 小さな原子のみにしか 適用できない。
リチウムのケースを見れば、この方法が まったく 非実用的で、大きな原子に使えないことが すぐに理解されることと思われる。
(Fig.39) 電子 1 の位置が同じでも 相手の位置関係で ヘリウムの関数が変化?
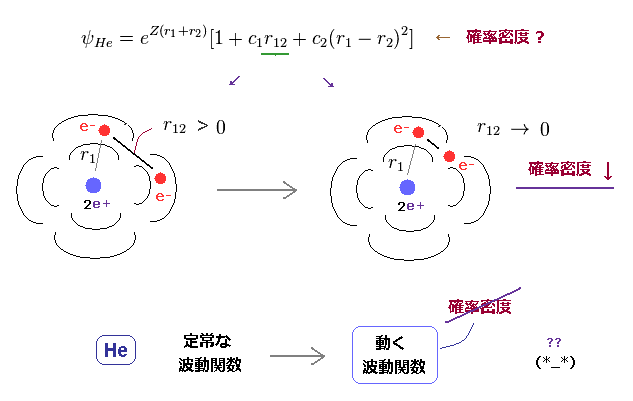
電子1が 同じ位置にいても、他の電子の位置に応じて 全体の確率密度が変化してしまう。
なぜなら この関数は 電子間距離 (= r12 ) を含んでいるからである。
つまり 電子間の反発を表そうとすると、 定常な確率密度波 という概念を "諦めな"ければならない。
(Fig.40) ヒレラス関数 + 変分法は 非現実的なくらい 複雑である。

すでに述べたように、単純なヘリウム原子でさえ 3000 以上もの項が 必要になる。
この関数は "s"、 "u"、 "t" などの変数を含む。
2つの電子間距離が 短く なるにつれて、全体の確率が 小さくなるため 避け合う電子を表現できたというわけである。
しかし これは 現実の電子の運動としては 不自然である。
例えば、 r12 が 短くなっても、2つの電子が 原子核の反対側にいれば、そのエネルギーは むしろ下がるはずである。
つまり、現実的な視点からすると、2つの電子だけでなく 原子核も考慮した位置関係で エネルギーの良し悪しを判断すべきなのだが、もちろん この関数でそこまで判断することは 不可能である。
(Fig.41) 計算結果が 実験値よりも低い? ← 換算質量 ?

このサイトにあるように、ヘリウムの計算結果は -79.013 eV で、この値は 実験値 (= -79.005 eV ) よりも低い。
この差は 原子核の運動、いわゆる換算質量の効果によると 言われている。
しかし 問題は 量子力学的な波動関数は 正確な換算質量を 予測できないということである。
(Fig.42) ヘリウムには 多くの異なった換算質量 (= μ ) が存在する。
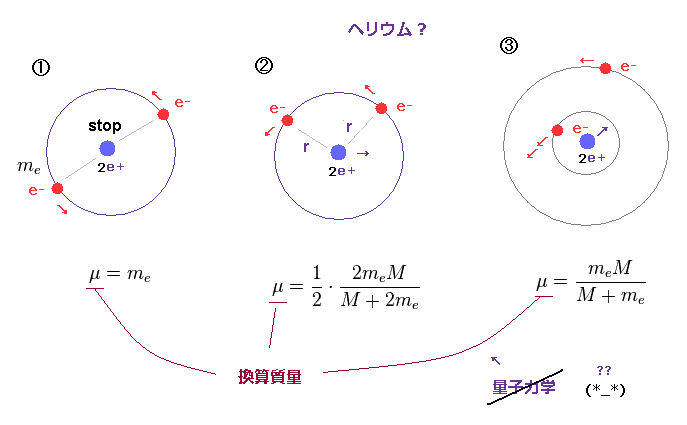
例えば、 Fig.42 左では、2つの電子が 原子核のちょうど正反対の位置で 動いている。
このケースでは、ヘリウムの原子核は 静止しているため、換算質量は 元の電子質量のまま ということになる。
Fig.42 真ん中では、各電子と原子核との距離が 共通の "r" である。
この場合では、換算質量を得るには "2m." (= m + m ) を使わなければならない。
Fig.42 右では、1つの電子のみが 原子核に近づいている。
このケースでは、他の電子は 遠く離れているため、原子核の動きに ほとんど影響を 与えない。
最後のケースでは 換算質量は "2m" ではなく "m" を使ってだす必要がある。
残念ながら、量子力学のヘリウムで これら異なる複数の換算質量を 正確に区別することは
不可能である。
つまり、計算結果自体の正当性が 疑わしいことになる。
(Fig.43) 2つの確率密度波が互いに避け合うのは非現実的なくらい難解である。

基本的に 波動関数は もともと"曖昧"な確率密度を表すためのものである。
つまり 単一電子の水素原子ですら、それは空間全体に 常に広がっている。
Fig.43 に示したように、これら 広がった波動関数 (= 電子雲 ) が 互いに避け合うことは 非常に不自然で不合理的である。
このことが 多体電子でのシュレディンガーの波動関数が 非現実的なくらい
複雑怪奇になってしまう要因である。
通常の 古典的な電子のほうが 至極 自然かつ 容易に 互いに反発する状態を 表わすのが可能なことは 明白である。
(Fig.44) 指数関数パラメーター "k" を 2.0 に固定 ? → 本当に変分法 !?

もちろんのことだが、 すべての種類の試行関数を試すことは 不可能である。
そのため 変分法による 最も低い値を知ることも 当然 不可能である。
例えば この論文 (p.3) では、指数関数部分のパラメーター K を 2.0 に 固定してしまって 正確な値を出したとしている。
"固定した" パラメーターは 当然 変分計算では ない。
Fig.28 のように このパラメーター "k" の種類を増やして 変分させるほど 計算結果は より低くなれる。
つまり このヘリウムの計算結果は 変分法の観点からして 疑わしいと言える。
この場合では、有効電荷 Z が "1" で 非現実的なヘリウム原子である。 .
( Fig.26 の Z = 1.6875 の場合と比較するように )。
(Fig.45)

この論文では、違う施行関数を使った時、指数関数のパラメーターを 5.0 < k < 8.2 の範囲に 人為的に制限している。
k = 2.0 の場合と k > 5.0 の場合の 値の開きは 非常に 不自然と 言わざるを得ない。
このケースでも、有効電荷 Z ( > 2.5 ) は 通常のヘリウム原子核 "2" のときよりも 大きくなっている。
またもや 非現実的な ヘリウム原子と言える。
(Fig.46) スレーター型の波動関数。
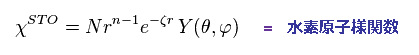
アブイニシオ ハートリー・フォック法、 CI 法は 基底関数の 選択 から始まる。
スレーター型の波動関数は 水素型の関数を用いている。 このサイト参照のこと。
シュレディンガーと ボーア模型では、すべてのエネルギー準位が 等しい。
このことが、現在の量子化学が 実験値とほぼ同じ値を与える 理由である。
(Fig.47) 指数関数のパラメーター = 有効電荷は リアルなもの ?
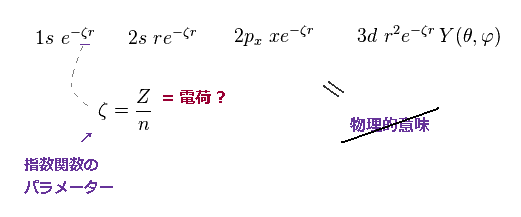
基本的に 指数関数部のパラメーター (= ζ ) は 有効電荷 Z を表す。
しかし Fig.32 や Fig.45 では、この有効電荷は 実際の原子核電荷を 越えてしまっている。
つまり 多体電子の波動関数には 物理的な意味というものは
存在しない と言っていい。
単なる ”数学的”なツールと 化している。
(Fig.48) ガウス型の波動関数。

スレータ型の波動関数は 正確なエネルギーを与える傾向にあるが、大きな原子では 使えない。
そのため ガウス型の関数 (= GTO ) が導入された。
(Fig.49)
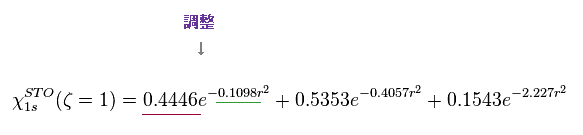
ガウス型関数で スレーター関数に似せるために 係数部 と 指数部 のパラメーターを調整する。
このサイト (p.6) や このサイト (p.18) にあるように、これらすべてのパラメーターは 分子計算のときに 固定して 用いる。
このことも、"アブ・イニシオ" 量子化学という名が 正しくない理由の1つである。
(Fig.50) 水素原子の指数パラメーターは 元の値から変更する。
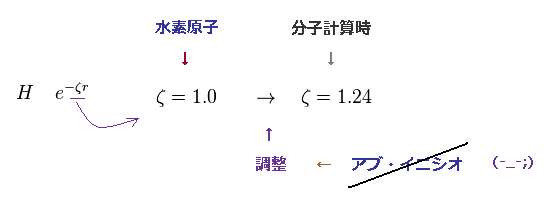
元の水素原子の指数パラメーターは もちろん "1" である。
しかし ほとんどの基底関数系では このパラメーターを 分子結合などに合わせるために
人為的に 1.24 に 変更している。
この 前もっての変更も アブイニシオとは 言えない。
(Fig.51) 固定 (= 収縮 ) した 基底関数は アブイニシオ ではない。
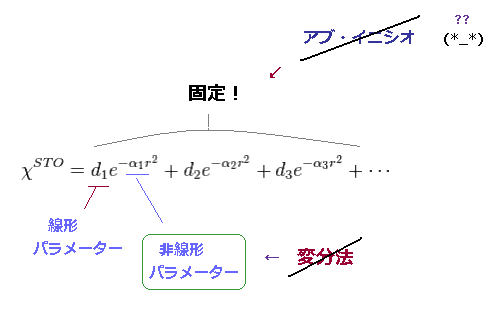
このサイト (p.6) や このサイトにあるように、 "アブ・イニシオ" 量子化学は ”本当の”アブ・イニシオ とは 呼べない。
ただ 各原子、分子に応じて それに合う基底状態を 選択しているだけにすぎない。
基本的に 指数関数部のパラメーター ( α = 非線形 ) は 非常に変分計算が難しく、複数あるときは ほぼ不可能である。 ( このサイト (p.19) ) 参照のこと。
係数部の いわゆる線形パラメーターのみ 変分計算ができる。
もちろんのこと、指数関数部分の変数の種類を増やして 独立に変化させて 最小値を探せば よりエネルギーを下げられる.
しかし 計算上の制限により、あらゆる試行関数を試せないので 変分法が本当に正しいのかどうかは 判断できない。
(Fig.52) 6-31G、ダブルゼータ型も アブイニシオではない。
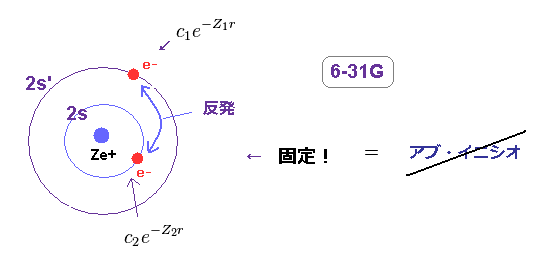
例えば、 6-31G 基底関数系では 2s の波動関数に 2つの異なる指数パラメーターの軌道を用意している。
なぜなら Fig.31 で述べたように、 異なる指数パラメーターを使用したほうが、反発エネルギーを低くできるからである。
あらかじめ用意した基底関数を用いることは 本当の アブ・イニシオでは ない。
(Fig.53)

基本的に 元の原子のみの関数を用いただけでは、正確なエネルギーに 到達
できない。
つまり 状況に応じて、分極関数や diffuse 関数などの 特殊な関数を付け加えていく。( 例えば、非実在の "1p" とか。 )
都合に合わせて 新たな関数を付け加えていく手法は 当然 アブイニシオとは呼べない。
さらに 基底関数重ね合わせ誤差という エネルギーの過大評価なども 人為的に取り除かない限り 必ず起きうるエラーである。
このサイト (p.4) など参照のこと。

2014/9/21 updated This site is link free.