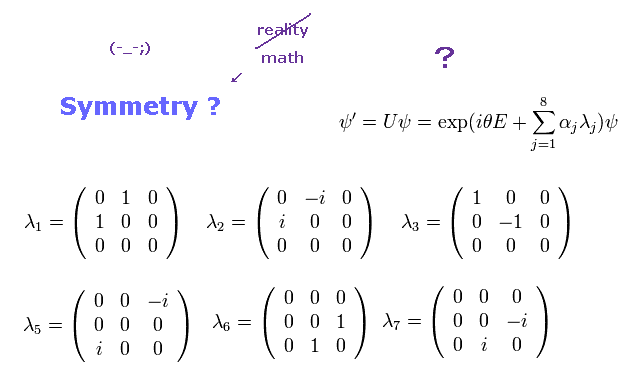
トップページ (2電子原子も含む正確な新ボーア模型)
相対性理論は間違っている。
素粒子物理学は本当なのか ?
QCDは 人為的なトリックに依存している。
(Fig.1) "対称性" とは 単なる数学的記号で物理ではない。
私達は しばしば 神の粒子、ヒッグス粒子が見つかり パズルの最後のピースがそろったというニュースを見聞きする。
よって 標準模型か完成し、正しいことが証明されたと。
しかし この標準模型が正しいとすると 物理と他の分野すべての発展はストップしてしまい 状況は かなり悪化してしまう。
このページに示したように、現在の標準模型は 完全に "数学上" の 対称性に依存している。
残念ながら これらの対称性は 単なる 数学的記号 であり、物理的実態が何もないのである。
彼らは 単に 抽象的な数式と遊んでいるだけで 永遠に リアリティーを目指そうとはしていない。
(Fig.2) 標準模型が正しい → 非現実的な ”ひも理論”と ”多世界”しか残らない。
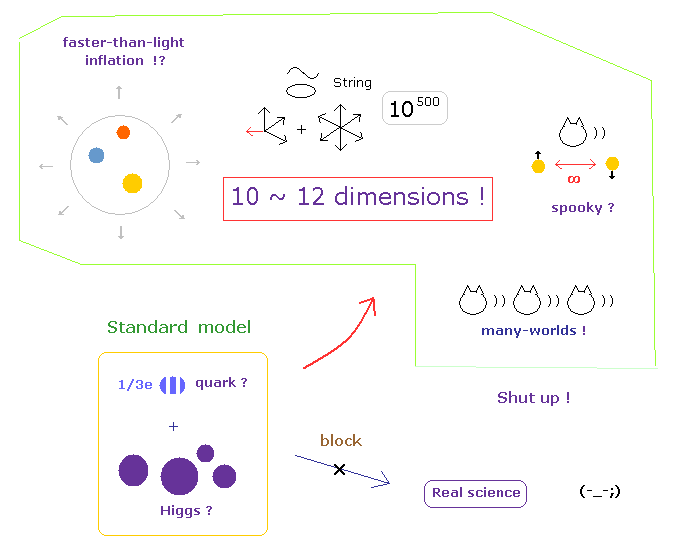
このページに示したように、40 年以上もの長い年月がたって、リアリティーのまったくない 10 次元の ひも理論だけが 統一理論として残ってしまった。
( ループ量子重力理論は 空間に対する非現実的な概念のために 統一理論として 完全に 失敗している。 )
つまり この標準模型を受け入れるとなると、明らかに 単なるフィクションといえる
余剰次元 を信じる必要が生じてくる。
これらのフィクションといえる余剰次元に加え、非常に抽象的な数学記号の羅列である ひも理論は 明らかに 他の科学分野の発展の足を引っ張り、かつ 多くの若くて優秀な才能を潰し続けている存在と言える。
さらに もし標準模型が正しいとすると、非現実的な 多世界様の重ね合わせ、超光速のインフレーション、不気味なリンクといった奇妙な概念を いやがうえでも 受け入れるしか 他に道は残っていない。
これは 非常に深刻な事態である。
この混沌とした状態で これらの奇妙な概念の実態を問おうとしても 彼らはただ口をつぐんで 明確な回答ができない (= Shut up and calculate ! の状態 )。
(Fig.3) すべての解釈は 理不尽である。 → 問うこと自体に意味がない?
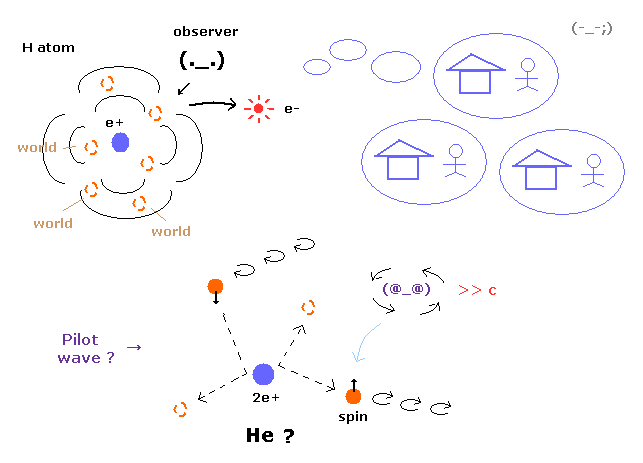
このページに示したように、1920 年代に コンピューターが なかったために 3体問題であるヘリウム原子を 現実的な模型を用いて説明することができなかった。
例えば、( 現実的な ? ) ガイド波理論を用いて ヘリウムを表そうとすると、2つの電子が 角運動量ゼロの s 軌道のために 頻繁に原子核にぶつかり続けて 現実とは大きく異なる 非常に不安定なヘリウム原子になってしまう。
そのため 彼らは 波動関数は 確率密度を示す 単なる数学的なツールにすぎないという 非実在的な考えを受け入れるしかなかった。
つまり "Shut up and calculate !" 解釈、別名 コペンハーゲン解釈と言える状態である。
もし この波動関数の一瞬の収縮を "局所的"な理論で示そうとすると、
非現実的な多世界解釈しか残ってしないのである。
つまり 標準模型が正しいとすると、量子解釈に関する 何の進展もない議論が 永遠に続くことになってしまう。
(Fig.4) エーテルが否定された → 仮想粒子、 暗黒物質、エネルギー、 ヒッグス.. = エーテル ??
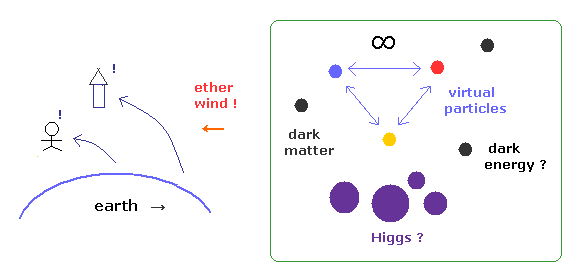
彼らは エーテルを否定したはずなのに 相対論的な場の量子論は 無限の仮想粒子、暗黒物質、暗黒エネルギー、ヒッグスなどの 多数のエーテル様の物質が 空間を埋め尽くしていることを必要とする。
一見して分かるとおり、この考え方は 明らかに エーテルを否定した 特殊相対論に
矛盾していると言える。
エーテルを否定したはずの 相対論的な場の量子論で このエーテルの種類が 逆に
増加してしまったからである。
ちなみに ヒッグス粒子は その対称性で弱い力を起こしたり、理論が繰りこみ可能な状態を保つために常に必須のため 現在の宇宙にも無限に空間に敷き詰められていることになる。奇妙である。
このページに示したように、特殊相対論には 致命的なパラドックス (= エーレンフェスト、 四角い電流回路, 直角レバー ) が存在する。
彼らが標準模型が正しいと認めるということは これらの致命的なパラドックスを 教科書から
永遠に隠し続けることを意味する。
結果的に 夢を持った 多くの新しい学生や 一般の人々が騙されて、彼らの人生が 狂わされてしまうことになる。
(Fig.5) 1/3 クォークは 絶対に単離できない → "クォーク" は 実在しない。
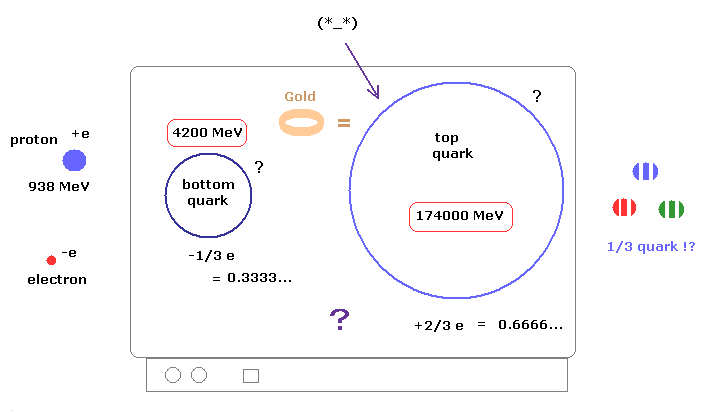
分数電荷 (= 2/3e, -1/3e ) は 今まで 観測されたことはない。 なぜなら クォーク や グルーオン は 単離することが絶対にできないからである。
それなのに どうして彼らは クォークが実際に見つかったと主張するのだろうか? これは 非常に奇妙である。
現在の標準模型には 素粒子の数が はっきり言って 多すぎる。
( つまり "素粒子" というワードは 不適切と言える。 )
クォーク (= 2 × 3 = 6 ) と レプトン (= 2 × 3 = 6 ) には 各3種類の世代というものがある。
驚くべきことに トップクォークは 素粒子にも関わらず 金原子 ほどの重さがある。ただし その電荷は 小さな分数電荷 2/3e なのにである。
陽子や中性子内などで 第一世代の素粒子しか安定にいられないことを考慮すれば、第二、第三世代の 不安定で役に立っていない世代は 加速器内でのみ現れる 素粒子の幻想の一種と言える。
(Fig.6) 電子と陽子 (= クォーク ? ) の深非弾性散乱。
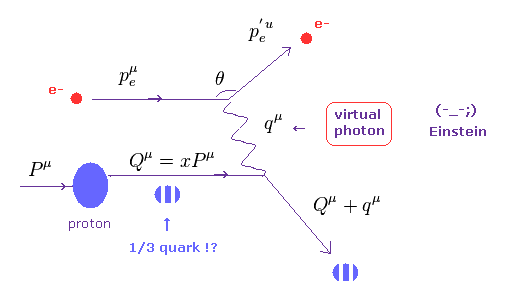
彼らは 高エネルギーの電子と陽子の 深非弾性散乱によって クォークの実在を確かめられたと主張している。
しかし 残念ながら これらの実験は 2/3e や -1/3e の分数電荷の証明には まったく
なっていないことを ここで説明する。
私達は 素粒子物理学のすべての反応経路を表すのに ファインマンダイグラムに必ず頼らなければならない。
しかし このセクションに示したように、ファインマンダイアグラムは 特殊相対論と矛盾する仮想粒子を 必ず含まなければならない。
Fig.6 では、 電子 (= e- ) が クーロン力で 陽子 (= P ) から散乱されている。
彼らは この過程で 電子が 陽子内のクォークに向けて 仮想光子 (= q ) を放出していると主張している。
(Fig.7) クォークが (= Q ) 陽子の "x" 倍の運動量を持っている。
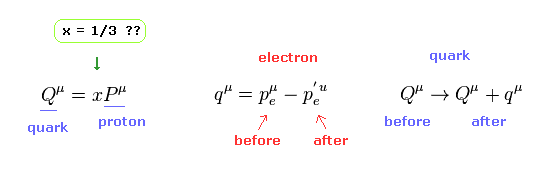
ここで 各クォークが 陽子の x 倍の 運動量 (= エネルギー ) を持つと仮定する。
この "x" が 1/3 のとき、 各クォークの運動量は 陽子の運動量全体の 1/3 倍になる。
Fig.7 は クォーク (= Q )、 電子 ( p, p' = 散乱の前と後 )、仮想光子 (= q ) の 4元運動量である。
これらの粒子は エネルギー・運動量保存則を満たす必要がある。
そのため エネルギー "q" (= 光子 ) が 電子から放出されて、クォーク (= Q ) に吸収されることになる。
(Fig.8) アインシュタインのエネルギー・運動量の関係式。
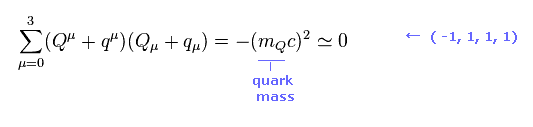
このページに示したように、各粒子は アインシュタインのエネルギー運動量の関係式を満足する。
ここでは ( -1, 1, 1, 1 ) バージョンの計量テンソルを使用する ( このページも参照するように )。
mQ は 各クォークの質量である。
ここでは クォークの小さな質量 ( mQ = 0 ) を無視する。 つまり Fig.8 は
(Fig.9)
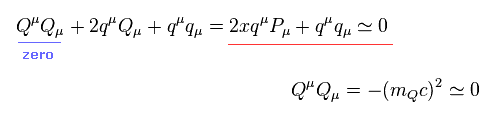
ここでは Fig.7 の Qμ = xPμ を用いた。
結果的に、
(Fig.10)
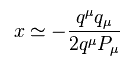
Fig.10 は ローレンツスカラー値であるため 計算値を同じに保ったまま 陽子 (= P ) に関して静止系を選ぶことができる。
(Fig.11)
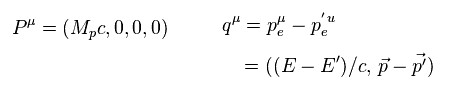
Fig.11 を Fig.10 に代入して 次を得る。
( 高エネルギーの電子の質量を ゼロと見なして。)
(Fig.12)
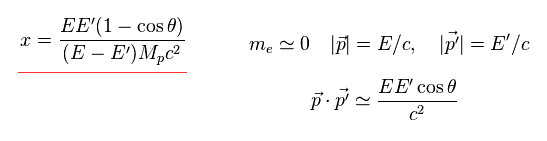
Fig.12 から、電子のエネルギー (= E, E' )、 陽子質量 (= Mp )、散乱角度 (= θ )を測定したとき、 "x" の値を知ることができる。
"x" に対する 電子分布の実験結果は、
(Fig.13) 各クォークは 陽子の 1/3 ではない。
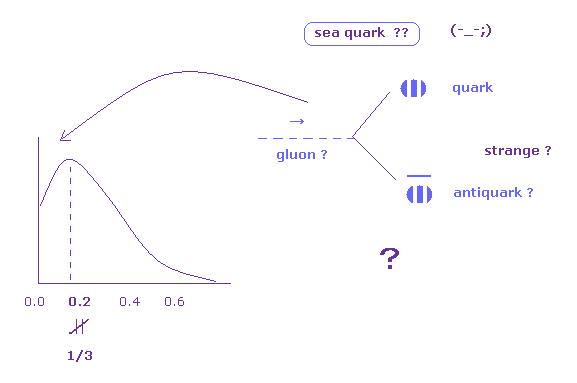
Fig.13 に示すように、各クォークのエネルギー ( 運動量 ) は 陽子全体の 1/3 未満である。
つまり これらの散乱実験は -1/3e、2/3e の分数電荷を まったく証明していないのである。
彼らは この問題を解決するために 非常に人為的な "海クォーク" なるものを導入した。
"海クォーク" とは 陽子内のグルーオンが 新しいクォークと反クォーク対を生成して それらは小さな運動量を持ち得るとしたものである。
これら 海クォークのために 各クォークの運動量は 1/3 未満になる。
しかし もちろん この海クォーク自体は直接観測できず、単なる想像上の産物にすぎない。
( このページも参照のこと。 )
(Fig.14) クォーク間の "カラー"ひもが切れる。 → 新しいクォーク対が出現 ?
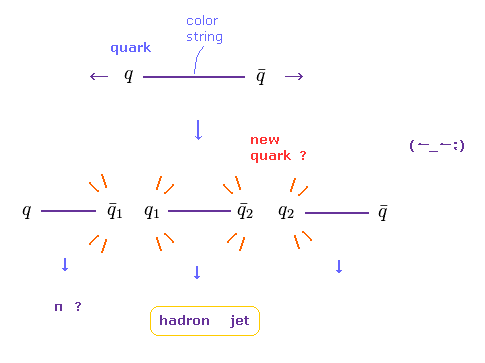
分数電荷のクォークは 決して 単離することができない。
彼らは いわゆる粒子跡の集まりである "ジェット" が 想像上のクォーク生成を意味していると主張している。
もちろん、この考えは 単なる憶測にすぎず、もし このジェットが クォークを意味していなかったとしたら、この時点で 標準模型は崩壊する。
QCD ( 量子色力学 ) によれば、2つのクォークを結合している カラーひもが切れても 新しいクォーク・反クォーク対が生成されて それらがハドロンジェットになると 主張している。
つまり 単一のクォーク自体は 絶対に分離して見ることができないというわけである。この理屈があまりにも出来すぎだと思われないだろうか?
もちろん、π 中間子などの ハドロンは 非常に不安定であるため、電子 ( 陽子 )、光子などの最終生成物から それらの実在を推定しているだけである。
( 非常に重要な "ニュートリノ"は 加速器では 観測できないのである。 )
(Fig.15) クォーク、 "グルーオン" の実験的証拠? それともフィクション?
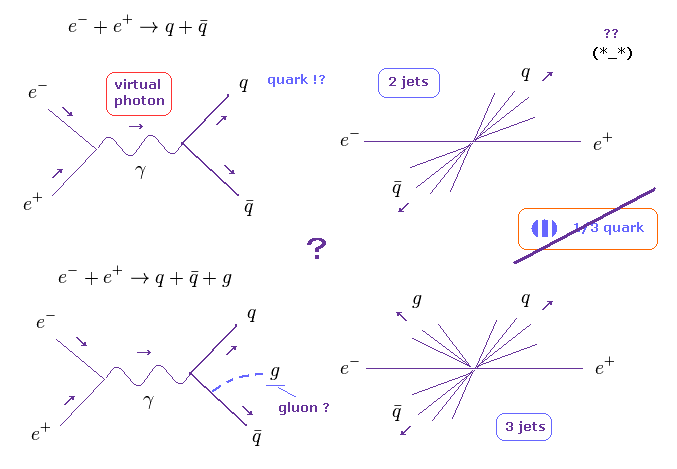
Fig.15 上では、電子と陽電子のペアが 仮想光子 (= γ ) に変化して その後 クォーク・反クォーク対 (= 2ジェット ) が生成されている。
もちろん、この解釈は単なる憶測にすぎず、そもそも この仮想光子自体 特殊相対論と矛盾しているのである ( このセクションも参照のこと )。
3つのジェットが観測されたとき、彼らは そのうちの1つは "グルーオン" に違いないを結論づけた。
この 非常に強引な解釈のみを信用して、彼らは クオーク・グルーオンの結合定数
(= gs ) を定義した。
( つまり この強い力の結合定数は フリーパラメーターであり、標準模型の予測とはまったく 関係がない のである。 )
(Fig.16) パウリの排他原理 = 絶対的な力を持った "神様" 的存在なのか?
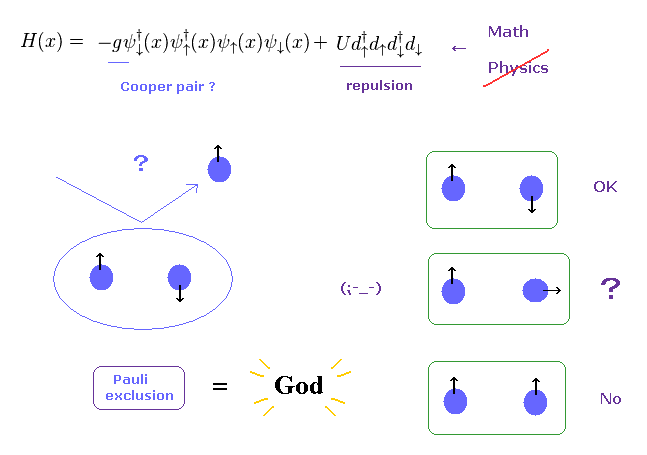
加速器内では、彼らは "スピン" の種類 ( 0、1、1/2 など ) を測定しようとしている。
もちろん、非現実的な スピン自体は 実際の回転とは 何の関係もなく、直接見ることもできない。
彼らは これらのスピンを 最終産物の崩壊パターンの偏りなどから推定しているの過ぎない。
( 光子のスピン1というのは 古典的な電磁波の偏光に相当する。 )
しかし この考えは 完全に 非現実的で リアリティーがないと言わざるを得ない。
このページに示したように、スピンの磁気モーメント (= 微細構造レベル ) は 弱すぎて、とてもじゃないが 超高エネルギーの加速器内では 完全に無視できる値である。
それなのに どうして彼らは このスピンを好んで使いたがるのだろうか?
主な理由は 彼らが パウリの排他原理を 絶対的な力を持った まさに 神 のように扱い、信じているからである。
(Fig.17) 単なる抽象的な 演算子では バライティーに富む 実際の現象を説明できない。
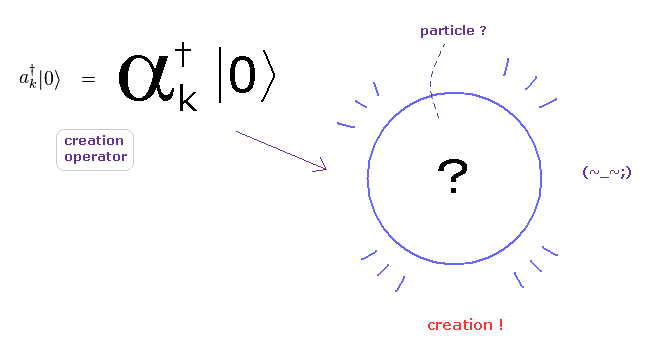
非現実的なスピンと 絶対的なパウリの排他原理のために、彼らは 必ず 抽象的な 数学上の演算子 ( スピンつきの ) に頼る必要がある。
現在の物性物理学、標準模型、ひも理論などの量子論では 様々な物理現象を記述するのに この非常に抽象的な演算子に 完全に頼っている。
このページに見られるように、これらの生成消滅演算子では 実世界の 様々なダイナミックに変化する現象を記述するには どう転んでも 限界がある。
なぜなら これらの生成 (消滅) 演算子では ただ漠然と 空間上に 粒子が生成 (消滅) したことのみを示せるだけで、具体的な変化に富む 時間、場所、位置関係を指定できないからである。
また 想像上の粒子 "光子" は これらの生成消滅演算子に 相互作用で 歩調を合わせるために 意図的に導入された存在といっていい。
(Fig.18) 全断面積 ( σ ) = 標的の的の大きさ。
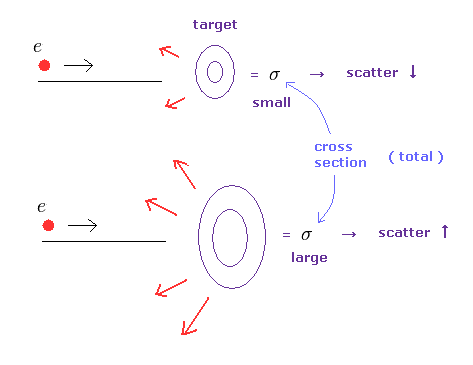
散乱団面積は 標的の面積の大きさを意味している。
つまり この断面積が大きいということは 標的の面積が大きく、すなわち より多くの散乱が観測されたという意味である。
(Fig.19) 散乱断面積 ( σ ) は "電荷" に関係しているが、クォークの電荷には関係ない。
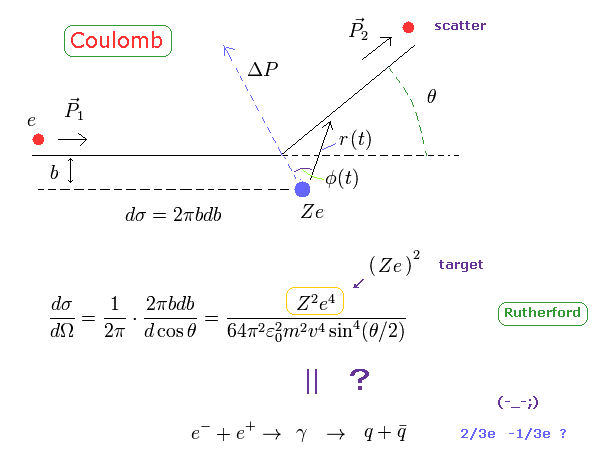
このページに示したように、古典的なラザフォードの クーロン散乱では、散乱断面積は 各電荷に 比例している。
Fig.19 では、電子 (= e ) が 正の原子核 (= Ze ) に散乱されている。
実際に 各粒子 ( 散乱の前後 2 × 2 = 4 ) の電荷が この断面積に関係している。
( 微分散乱断面積 (= dσ) とは 各散乱角度 θ に対する 無限小の断面積の意味である。 )
この古典的なラザフォード散乱は クーロン力によるため、各粒子の電荷の大きさが 散乱(角度) に影響を与えていることは普通のことである。
問題は e- + e+ → 仮想光子 → クォーク・反クォーク という生成反応においてさえ、 各粒子 ( クォーク ) の電荷が 本当に影響を与えているのかということである。
(Fig.20) ローレンツ力 → ファインマンダイアグラム → "電荷" = 散乱 ?
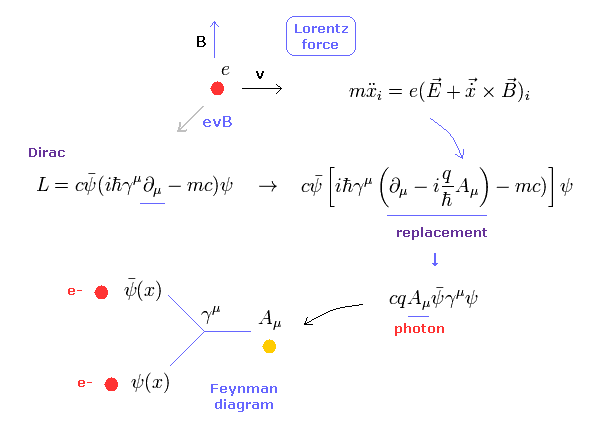
このページに示したように、QED における 電子と光子間の相互作用は 古典的なローレンツ力に起因している。
QED では、光子は 磁気と電気ポテンシャル (= A, φ ) で表される。
ディラックのラグランジアンで 演算子の置きかえをすれば、ファインマンダイアグラムを与える 相互作用項を得ることができる。
また この相互作用の形式が QED における 電子と光子の 唯一の相互作用となる。
つまり "数学上の" QED には 何の物理的なイメージがないことを覚えておく必要がある。
唯一の形式のために クォーク・反クォーク対の生成においても この相互作用項が使用される。
結果として、結合定数である 電荷 "q" (= Ze ) が すべての種類の散乱振幅に関係していると 彼らは主張している。
(Fig.21) しかし 電子・陽電子対消滅は クーロン散乱とは まったく異なるものである。
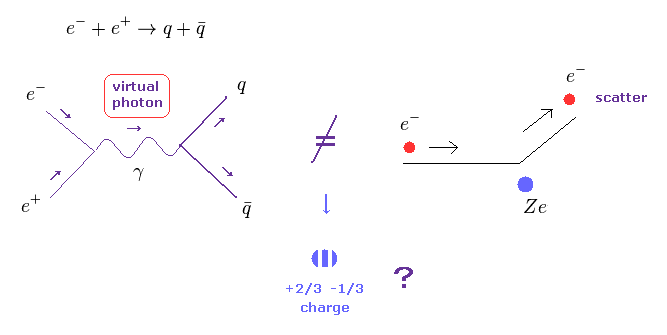
Fig.21 を見てのとおり、電子・陽電子対消滅は 通常のクーロン散乱とは 完全に異なるものである。
なぜなら、通常のクーロン散乱 ( ex. 電子が陽子に散乱される ) では、各荷電粒子は まったく消失することなく それらは単に お互いを散乱するだけだからである。
Fig.21 左では、電子と陽電子が 消滅して 仮想光子に変化し、 新たなクォーク・反クォーク対が生成されている。
つまり これらの過程は 根本的に性質の異なるものなのである。
よって 想像上のクォーク対が新たに生成されて その分数電荷の大きさが この生成 (散乱) 頻度に関係しているという考えは 非常に不合理であり 強引な解釈といえる。
(Fig.22) 分数電荷の実験的証拠 ??
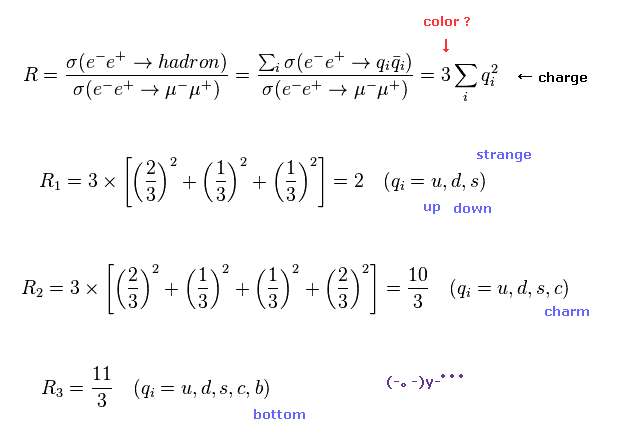
そのため 全断面積は 新たに生成されたクォークの各電荷の2乗に 比例していると 彼らは主張している。
( 各クォークは 絶対に 単離できないのにである。 )
各クォークには 3種類の色 (= 赤、 緑、 青 ) があり、このそれぞれに まったく同じ確率で 生成されると 彼らは主張しているのである。
( もちろん この主張は 直接確かめられない。単なる憶測にすぎない。 )
さらに アップ、ダウン、ストレンジ、チャーム、ボトム クオークなどは それぞれ 全く質量が異なるのに それらの生成確率は 完全に等しいと仮定しているのである。
( 例えば ボトムクォークは アップクォークの 1000 倍以上もの重さである。 )
(Fig.23) 分数電荷の実験的証拠 ??
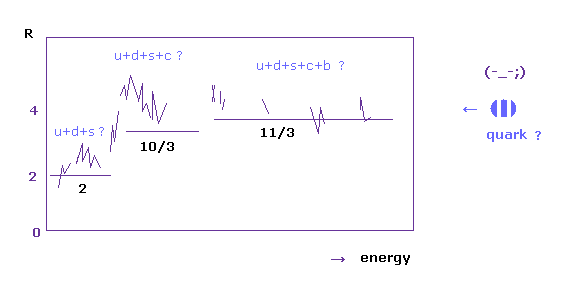
Fig.23 は ミューオンとクォーク生成比であると 彼らは主張している。
Fig.23 を見て分かるとおり、散乱結果の値は 上下に非常に揺れていて まったく1つに定まっていないのである。
つまり Fig.22 の結論づけは 非常に強引であると言える。
各ジェットが クォークを実際に示しているという 確たる証拠も まったくない。
つまり クォークの存在は 完全に標準模型の 仮定に仮定を重ねたものに依存しているといっていい。
(Fig.24) "up"、 "down"、 "bottom" クォークの生成確率はまったく同じ?
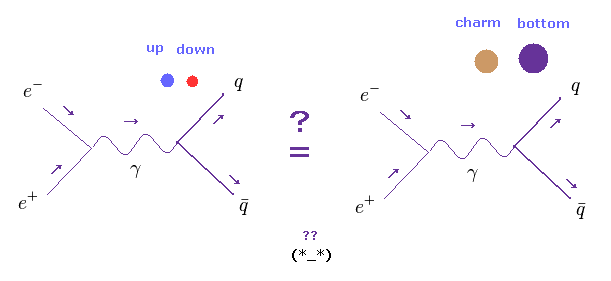
ご存じのとおり、宇宙には 水素やヘリウムなどの 非常に軽い原子の数が 他の重い原子に比べて 非常に多い。
つまり 軽い粒子 (= up, down クォーク ) が 重いクォーク (= charm, bottom ) よりも より多く生成されるのが 自然なことと言える。
つまり Fig.22 解釈は 非常に 不自然と言える。
(Fig.25) 漸近的自由の実験の証拠 ??
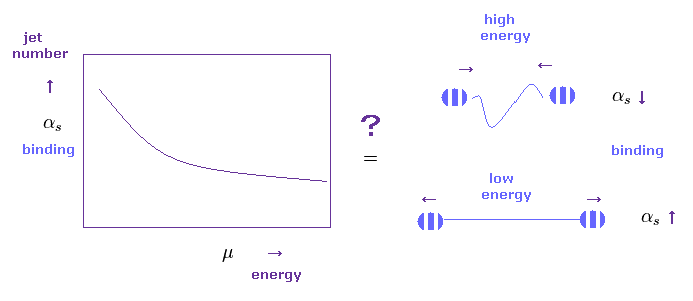
彼らの主張によれば、クォーク間のカラーひもが短く (= 高エネルギー ) になるほど このひもの力が
弱くなるらしい。
一方で、この距離が長くなると (= 低エネルギー )、このひもの力が強くなる。
( もちろん これらの考えは 単なる想像上の産物にすぎない。 )
ファインマンダイアグラムの相互作用によれば、結合の強さ (= 結合定数 ) が大きくなれば 散乱される数 (= ジェット ) が多くなる。
よって Fig.25 のデータは クォークの漸近性自由の証拠だと結論づけた。
しかし 残念ながら これらの非間接的なデータのみから この奇妙な性質を確定することは はっきり言って できない。 .
(Fig.26) 強い力の結合定数 ?
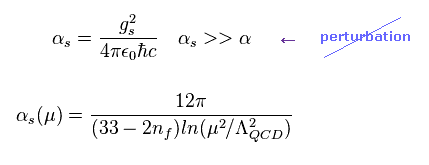
彼らは 強い力の 結合定数 (= 力 ) が Fig.26 のように変化すると仮定した。
もちろん この定数 gs は フリーパラメーターの1つで 標準模型そのものから 予測することは できない。
Fig.26 では、 エネルギー (= μ ) が 大きくなるにつれ、 結合力 (= α ) は 弱くなる。
この 漸近的自由の奇妙な性質のために 結合定数は 低いエネルギーエリアで 強くなりすぎてしまう。
そのため 量子色力学 (QCD) は 量子電磁力学 (QED) のような摂動計算をして 何かを予測することができない。
( 近似的な数値計算をするしかない。 )
(Fig.27) Fig.25 の結果の自然な解釈。
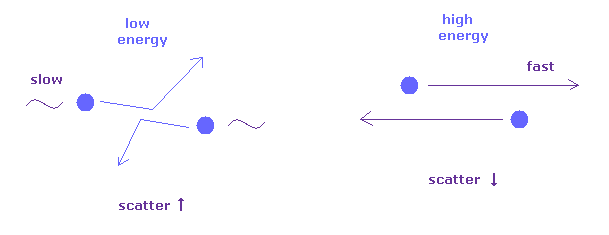
常識的な視点に立てば、高エネルギーの 非常に速い粒子は お互いに通りすぎる際に
そのハイスピードのせいで 散乱されることなく通り過ぎてしまうといえる。
低エネルギーで遅くなれば、通り過ぎる際に 相互作用によって散乱される確率が高くなる。
この解釈のほうが 想像上のクォークや 奇妙な自由性の考えよりも 現実的で自然である。
このカラーひもが真実だとしたら、このひもの起源や どのように生成されるのかを具体的に答える必要がある。 "Shut up and calculate !" と言うだけで 明確な回答を避けてばかりでは これらの概念が 嘘であると言っているに等しい。
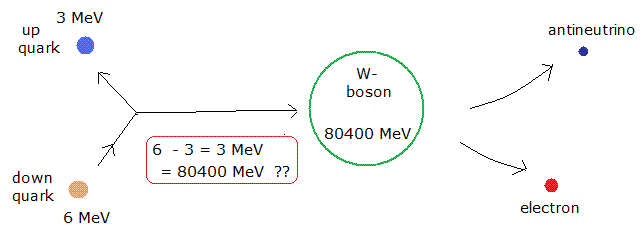
(Fig.28) 非常に重い W ボソン (= 陽子の 80 倍 ) は 実在するのか?
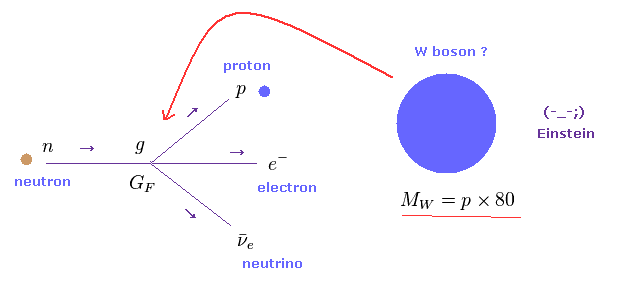
ベータ崩壊では 中性子が 電子と反ニュートリノを放出して 陽子に変化する。
中性子と陽子の質量エネルギーの差は 非常に小さい。
そのため 陽子の 80 倍もの重さの 非常に重い W ボソン が この過程で突然生成されるという考えは 非常に 無理がある。
この反応過程は 明らかにエネルギー保存則を破っている。
そのため この大きな食い違いを説明するために 彼らは 非常に "便利な" 時間とエネルギーの不確定性原理に頼ることにした。。
しかし この 非現実的な標準模型の解釈が 真実だと思われるだろうか?
(Fig.29) 弱い力の結合定数 ?
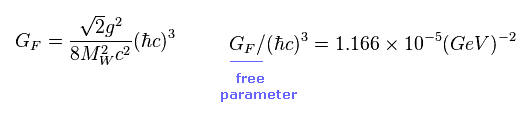
GF は 弱い力の結合に関与する フリーのパラメーターである。
この値は 標準模型自体から 予測することができず、ベータ崩壊の平均寿命などから推定するしかない。
(Fig.30) W ボソンの質量 ?
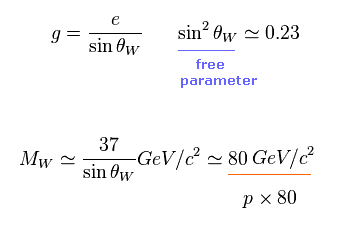
結合定数 "g" も フリーのパラメーターで 標準模型自体から 予測することが できない。
このページに示したように、 この "g" は ワインバーグ角 θW を用いて表される。
この角度も フリーのパラメーターである。
( これらの片方が決まると もう片方も決まる。)
Fig.29 と Fig.30 から、 W ボソンの質量が決まる。
もちろん Fig.29 の GF 内の MW が 本当に W ボソンの質量を表すのかは 単なる仮定にすぎない。
すでに述べたように、この W ボソンの質量が本当だとしたら、エネルギー保存則が完全に破れていることになる。
(Fig.31) Z ボソンの質量 ?
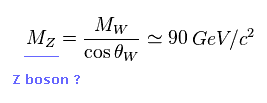
もし 角度 θW が 何かの実験で決まると Z ボソンの質量も決まる。 .
もちろん、この "Z ボソン" 自体は 電弱統一のために導入された 人為的な中性の粒子である。
彼らが sin, cos θW を定義した瞬間に この新しい Z 粒子も 導入することになる。 .
(Fig.32) β - 崩壊 ( 中性子 → 陽子 + 電子 + 反ニュートリノ。 )
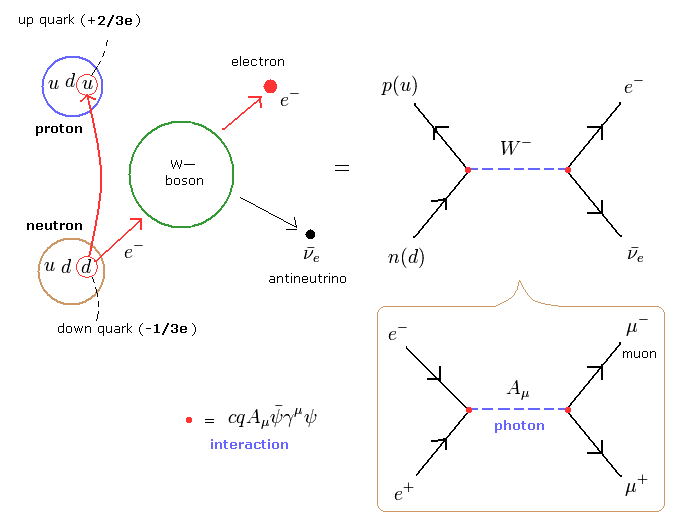
すべての反応経路は ファインマンダイアグラムに従わなければならない。
この過程では、中性子内の down クォーク が 重い W ボソンを放出して 陽子内の up クォークに変化する。
そして この W ボソンが 電子、反ニュートリノに変化すると 彼らは主張している。
このセクションに示したように この W ボソン (= 中間の線 ) は 特殊相対論に 反する仮想粒子である。
つまり 標準模型は 最初から 自己矛盾を含んでいることになる。
(Fig.33) W ボソンの崩壊確率。
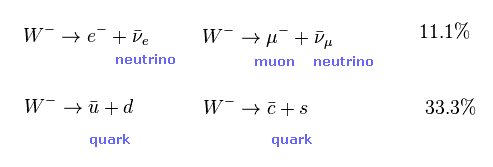
W ボソンは 電子やニュートリノよりも クォークに より多く崩壊すると 彼らは主張している。
しかし 彼らは Fig.33 の下の クォークの崩壊モードを用いようとしない。
なぜなら クォークやグルオーンは 強い力で ランダムに散乱されることがあり、かつ その確率が W, Z ボソンの生成確率よりも大きいからである。
(Fig.34) W ボソンの実験的証拠 ?
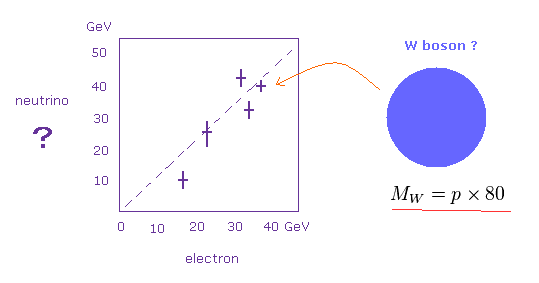
重要な点は 私達は 地球でさえ簡単に貫ける ニュートリノを 測定できないということである。
生成されたニュートリノの数を知るには、彼らは 生成されたであろう すべての粒子を測定する必要がある ( はっきり言って 不可能である。 )
このときに 何らかのエネルギーの偏り (= 消失 ) があれば これが 見えないニュートリノの証拠だと 彼らは主張している。
しかし この仮定は 単なる推測にすぎず かなり無理があると言える。
なぜなら 非常に稀な W ボソンに生成に比べて ほぼ無数の 関係ない 雑音粒子が存在するからである。
つまり この見えないニュートリノの過程は 非常に疑わしいと言える。
Fig.34 に示したように、 約 80 GeV 付近 (= 電子 + 見えないニュートリノ ) に 何らかの共鳴ポイントがでる。
( しかし 80 GeV 以外にも この共鳴ポイントが存在する。)
(Fig.35) Z ボソンの崩壊モード。
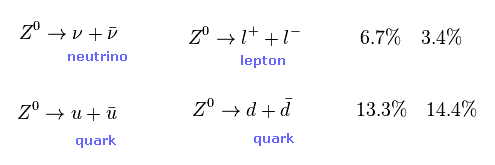
Z ボソンのケースでも 彼らは Z ボソンの質量を 最終産物の散乱イベント (= 断面積 ) から推定しているだけである。
つまり 不安定な W、 Z ボソン自体 直接観測することができない。
( これらの非常に不安定な粒子は 霧箱内ですら見ることができない。 )
(Fig.36) 加速度内の W ボソンは β崩壊のとは まったく異なるものである。
W と Z ボソンの比は Fig.31 の比で予測できる。
そのため この関係式と一致させるような 共鳴ポイント (= フリーパラメーター ) を探したといっていい。
この共鳴ポイント ( もしくは ワンバーグ角 θW ) は フリーパラメーターで 標準模型では 予測できないものである。
結果的に この共鳴ポイントは 非現実的に重い W ボソン を与え、これは 見事にエネルギー保存則を破っているのである ( Fig.36 )
あなた方は この極端に重く 加速器内でしか出現しないであろう W ボソンが 本当に 通常のβ崩壊に関係していると思われるだろうか?
標準模型に合わせるために 彼らは この非現実的に重い W ボソンを受け入れるしかなかったのである。
( このページも参照のこと。 )
(Fig.37) 平均寿命と崩壊幅 = 不確定性原理は リアルなのか?
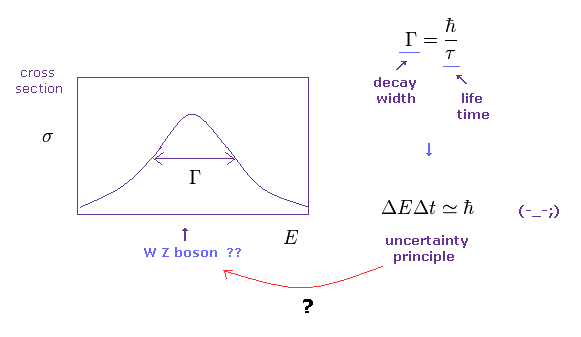
高エネルギーの加速器内で起きる事象の解釈において 彼らは 完全に
時間と空間の不確定性原理に頼っている。
つまり この前提条件が間違っているとすると、現在の標準模型の解釈も間違いということになる。
Fig.37 の エネルギー (= 質量 ) の不確定性 (= 幅 ) が 広くなるほど、時間の不確定性が 小さくなる (= 寿命が短くなる ) と 彼らは主張している。
そのため 彼らは 線の広がり幅は 崩壊幅を表し、つまり どれだけ容易に粒子が崩壊するかを意味していると主張している。
もちろん これらの解釈は単なる憶測にすぎず まったくその根拠がない。
Fig.37 データは ある散乱粒子の分布の1つを示しているだけで はっきり言って 新粒子の生成だとか寿命だとかには 何の関係もないと思われる。
(Fig.38) ニュートリノの "3つ"の世代の実験的根拠?
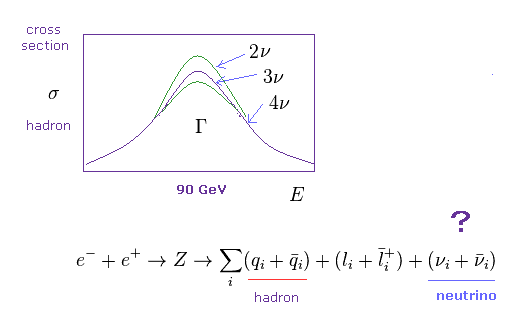
上で述べたとおり、見えないニュートリノは 非常に重要にも関わらず 直接観測することが
できない。
彼らは Fig.37 の崩壊幅が これらの見えないニュートリノも含んだ トータルの崩壊確率だと主張している。
( もちろん、この仮定は まったくの "想像上" の産物にすぎない。 )
つまり 他のハドロンの散乱事象をすべて測定できれば、残りのニュートリノの崩壊確率を推定できると 彼らは主張している。
この差が大きいとき、見えないニュートリノの世代の数が大きいということになる。
この根拠のない仮定をもとに、彼らは この実験 (= Z ボソンの崩壊 ) が ニュートリノが
3世代あることを示し、正しさが証明されたと主張しているのである。
しかし 最近の LSND や MiniBooNE などの結果では 4世代目のニュートリノを示唆するデータがでている。
そもそも ニュートリノ振動 (= ニュートリノの質量 ) 自体 標準模型とまったく
矛盾した結果である。
彼らは 従来の標準模型と 矛盾した結果がでたとしても 決して 標準模型自体を否定しようとはしない。
( こういうときは 非常に 便利に 標準模型を"超えた"現象と 言葉を刷り変えてしまう。 )
(Fig.39) 中性の Z ボソンの実験的証拠?
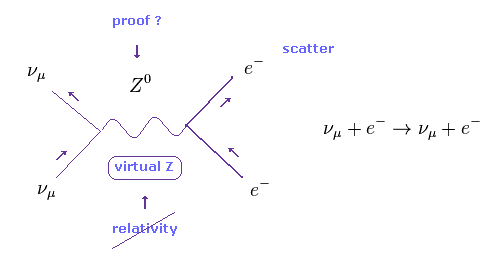
彼らは ニュートリノが 電子の運動に影響を与えているのを発見したとき、この現象は Z ボソンの存在の証拠だと結論づけた。
しかし もちろん 非常に重い Z ボソン自体見ることはできない。
単純な解釈をすれば、ドブロイ波 (= ニュートリノ ) が 電子を少し散乱させただけの現象である。
つまり 非現実的な Z ボソンは まったく不要な産物なのである。
あなたがたは 陽子の 90 倍もの重さの Z ボソンが 突然現れて この反応仮定に本当に関与していると思われるだろうか?
(Fig.40) カイラル対称性の自発的な破れ = 核の質量の 98 %。

実は 原子核の質量の 98 % は カイラル対称性の破れによって起きるとされ 質量のたったの 2 % が ヒッグス機構によって生じると言われている。
それでは このカイラル対称性の破れとは いったい何なのだろうか?
残念ながら Fig.40 に示しすように このカイラル対称性の破れ (= QCD ) には 何の具体的な
イメージがないと言っていい。
( 見てお分かりのとおり、単なる”数学上の記号”である。 )
Fig.40 では、彼らは 近似的にに クォークの質量をゼロとし、左巻き (= L )と 右巻き (= R ) クォークを分離させた。
他の力のように このラグラジアンは 対称性、いわゆる L と R それぞれ独立に 位相変換の下で不変である。
これを "カイラル対称性" という ( SUL(2) × SUR(2), SU(2) は 2 × 2 行列の意味である )。
(Fig.41) 対称性の破れ = クォーク・グルーオン凝縮 ?

真空が L と R の場の混合したものを含んでいるとき、それは 位相変換のもとで 不変ではなくなる(= カイラル対称性の破れ )。
この状況で、彼らは クォークと反クォークの多くのペアが 小さな陽子の内部に 充満していると主張している。
この QCD の機構によって 陽子の 98 % の質量を説明できるとしている。
この強い力は 結合定数が大きいために QED のような 通常の摂動計算が使えない。
そのため 彼らは 何らかの近似的な数値計算に頼るしかない。
残念ながら この理論には まったく 現実的な物理的根拠がないといっていい。
( このページも参照のこと。 )
(Fig.42) 大統一理論 (= GUT ) ?
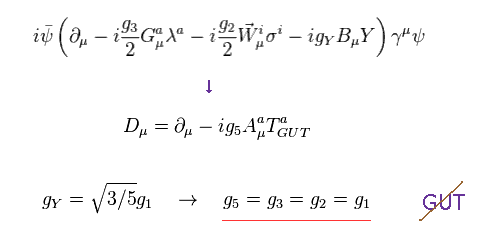
実は 現在の理論は 電磁気力、弱い力、強い力 の3つの基本的な力の統合をできていないのである ( 重力を除いても )。
これらの力をすべて統合するには ある高エネルギー領域で 3つの力の結合定数が 1点に交わる必要がある。
SUSY-GUT (= GUT + 超対称性 ) は この問題を 新たなパラメーターを導入して解決することができる。
つまり 超対称性は 統一理論に必要不可欠と言える。
(Fig.43) ヒッグスの質量の階層性問題?
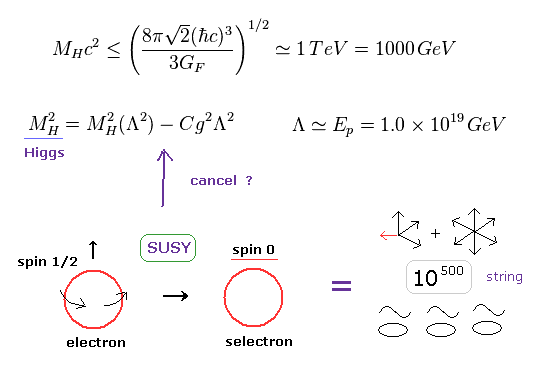
現在の標準模型は ヒッグス粒子の質量を まったく予測することができない。
さらに このヒッグスの質量が ある臨界点 (= 1 TeV ) を越えると、標準模型は崩壊してしまう。
( つまり 126 GeV の ヒッグスは 範囲内にあることになる。 )
ヒッグス・クォーク・ゲージ粒子の自己相互作用により、ヒッグスの質量は プランクエネルギー
(= 1019 GeV ) レベルほどに発散してしまう。
現実的な ヒッグスの質量 (= 126 GeV ) を得るには、この補正項を オリジナルのヒッグスの質量 (= これもプランクエネルギーぐらい ) でキャンセルさせる必要がある。
超対称性は このキャンセルを行える 唯一の手法である。
つまり 超対称性は この数学的な ( 物理ではなく ) 理由で 必要不可欠な存在といえる。
このキャンセルは ほとんど 無限大 マイナス 無限大の規模であり、はっきりいって まったく現実性がなく 不自然な 数学上のトリックと言える。
さらに 超対称性は ひも理論で 26 次元から 10 次元に変えるのに必要不可欠である。
( はっきり言って どっちの次元でも 非現実的ではあるが・・ )
(Ap-1) クーロン散乱 → 仮想光子 → アインシュタインは間違い ?
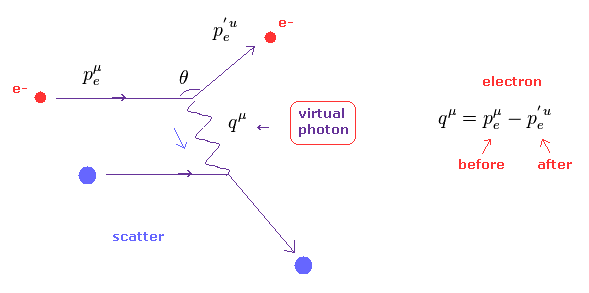
ご存じの通り、QED、 標準模型、ひも理論などの 相対論的な場の量子論は 特殊相対論を満たす必要がある。
しかし 実際は これらの相対論的な理論は すべての反応において 特殊相対論を 破っているのである。
Ap-1 は 電子 (= e-, 赤 ) が ある荷電粒子 (= 青 ) によって散乱される過程を示している。
これらの過程では、彼らは 標的の粒子と 光子を "交換"すると主張している。
この光子が "仮想光子" と呼ばれ、特殊相対論を 満たさないのである。
(Ap-2) 散乱の前後の 4元運動量。
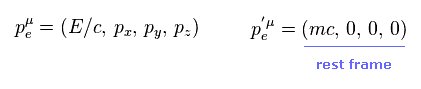
Ap-2 は 電子の 散乱前 (= p ) と 後 (= p' ) の 4元運動量 を表している ( このページも参照のこと )。
ここでは 散乱後の電子 (= p' ) に対して静止した系を考える。
"E" は 相対論的なエネルギー、 "p" は 電子の運動量の各成分を示している。
(Ap-3) 4元運動量の関係式。
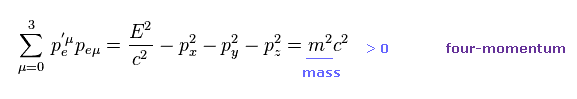
これらの 4元運動量は すべての慣性系で Ap-3 の式を満たすことが知られている。
このセクションでのみ ( 1, -1, -1, -1 ) バージョンの計量テンソルを使用する ( このページを参照のこと )。
Ap-3 を見て分かるとおり、この式は 必ず 正の値になる。なぜなら質量の2乗が 正の値だからである。
しかし 仮想光子の場合は この値は 必ず 負 の値になる (= いわゆる タキオンである )。
この事実は 明らかに 相対論的な標準模型が 自己矛盾を含んでいることを示している。
(Ap-4) エネルギーの保存。
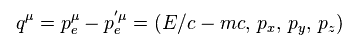
Ap-1 では、 電子 "p" が 光子 q を放って p' になっている。
そのため エネルギーと 運動量の各成分が 保存されなければならない。
結果 光子 q の運動量は Ap-4 のようになる。
(Ap-5) 光子 "q" の エネルギー・運動量の関係式
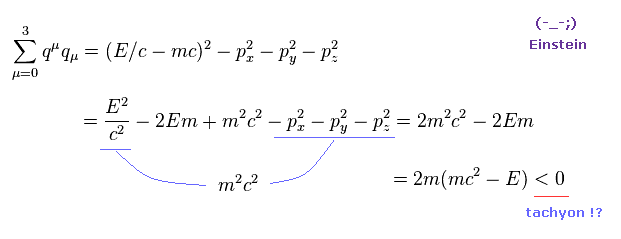
この光子 q の エネルギー・運動量の式 ( Ap-3 を参照 ) は Ap-5 のようになる。
Ap-3 を用いて、この光子 q の スカラー値である質量が負 の値になることを示せる。
これはつまり この光子は アインシュタインが 決して認めなかった "タキオン" ということになる。
qμqμ は スカラー定数であるため、 すべての慣性系で この値は 必ず 負の値になってしまう。
重要な点は 現在の素粒子物理学は この奇妙なタキオンに 完全に 依存しているのである。
これは つまり 標準模型は 間違いであることを意味している。
(Ap-6) 電子 + 陽電子 → 仮想粒子 → クォーク ?
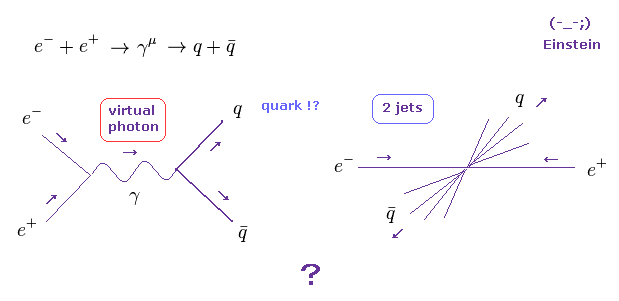
加速器内では 電子 ( e- ) と 陽電子 ( e+ ) の消滅過程が クォーク、W、 Z ボソンなどの新しい粒子の生成に しばしば用いられる。
しかし実は これらの過程は 必ず 特殊相対論に矛盾しており、すなわち これらの新しい粒子は 非実在のものであることを示している。
( W、 Z 粒子自体は 非実在の仮想粒子である。 )
Ap-6 では、電子と陽電子が消滅し、仮想光子 (= γ ) に変わり、クォーク・反クォーク対が生成される。
( もちろん これらのクォークは決して単離できないため、単なる 想像上の粒子にすぎない。 )
(Ap-7) 重心系における エネルギー・運動量。
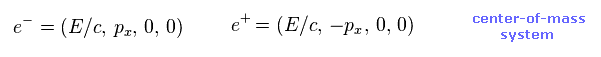
Ap-7 は 電子と陽電子が ちょうど逆方向から飛んできて 衝突する系である ( Ap-6 右を参照 )。
この 重心系では、エネルギー E は 完全に同じで 運動量の方向が ちょうど逆である。
( "px" と "-px" は それぞれ 電子と陽電子である。)
(Ap-8) 仮想光子 γ のエネルギーと運動量。
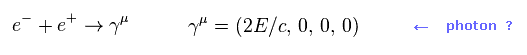
結果的に Ap-7 の各成分を足して、Ap-8 の光子のエネルギーと運動量を得ることができる。
( ここでは "γ" は γ 行列ではなく γ 線の意味である。 )
一目見て Ap-8 のこの光子が 実在のものでないことが分かる。
(Ap-9) なぜなら この光子の質量はゼロでないからである。
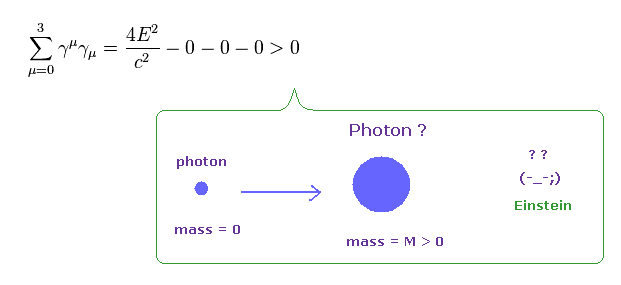
この光子 γ のエネルギー・運動量の式は 正の質量を与える。
この 質量を持つ光子は 明らかに 特殊相対論に矛盾している。
つまり 現在の標準模型のすべての新しい粒子や反応過程は 特殊相対論と 矛盾しているのである。
再び、この事実は 現在の標準模型l (+QED、超弦理論 ) が 間違いであることを意味している。
(Ap-10) 陽電子 (positron) は 実在の粒子もしくは "空孔 (hole)" なのか ??
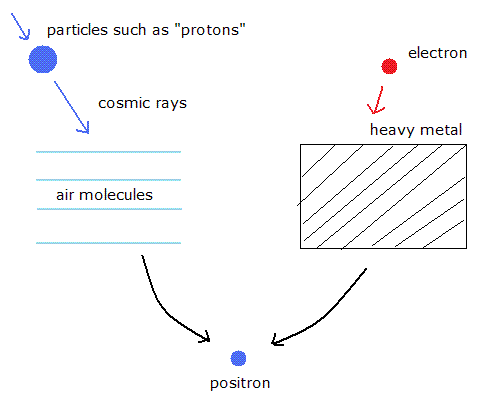
陽電子は 1936 年に アンダーソンによって発見された。
その実験の後でさえ、彼の先生であった ミリカン や ディラックはその存在を疑っていた。
実際に ほんのわずかしか陽電子様の粒子は 霧箱の中で発見されなかった。
陽電子は 量子論によれば 真空から生じるとされている。
しかし実際には、陽電子を発生させるとき、電子を 重金属などのものにぶつけなければならない。(真空でなく。)
また、宇宙線の中の陽電子は 陽子などの粒子が 大気の分子 (真空でなく)などにぶつかることによって発生される。
(Ap-11) どうして 重金属の原子核が 陽電子発生に必要なのか?
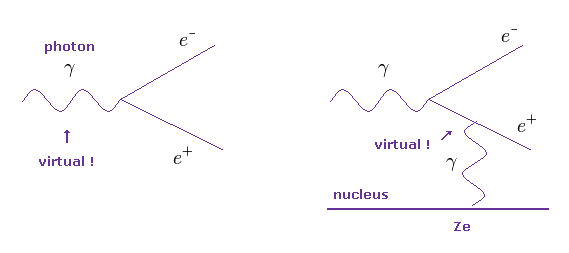
Ap-11 左 と Ap-6 に示したように、 もし原子核がないと、電子陽電子対を生成する光子が 特殊相対論に反する 仮想光子になってしまう。
一方で ある原子核が この過程に絡んでいると、仮想粒子は 中間の線として隠すことが可能になる (= Ap-11 右 )。
だから 重金属の原子核が必要だと 彼らは主張しているのである。
しかし あなた方も感じられたように、理不尽な仮想粒子そのものの存在が 中線、外線に関係なく まったく 実在性のないものであることは言うまでもない。
(Ap-12) どっちが起きる ?
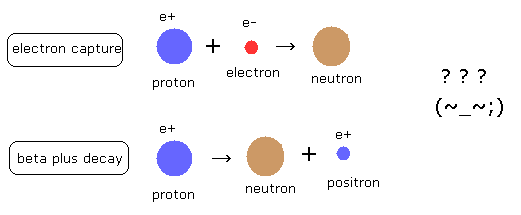
ベータプラス崩壊 (beta plus decay) と 電子捕獲 (electron capture) は 同じ原子核を生じさせる。
それらの両方とも、原子核内の 1つの陽子を 中性子に変化させる。
もちろん これらの反応は 原子核において 最終生成物が エネルギー的になりやすいときにのみ起こる。
結果、両反応とも エネルギーを放出する。
しかし ご存じのとおり、中性子は陽子よりも少し重い。
つまり 陽子が陽電子を放出する反応は エネルギー保存に違反している。
彼らは 他の粒子との相互作用を考慮すれば解決できるとしているが ファインマンダイアグラム自体 単独の反応を許しているので この奇妙な反応が許されることになる。
(Ap-13) "どこで" エネルギーが放出されるのか ?
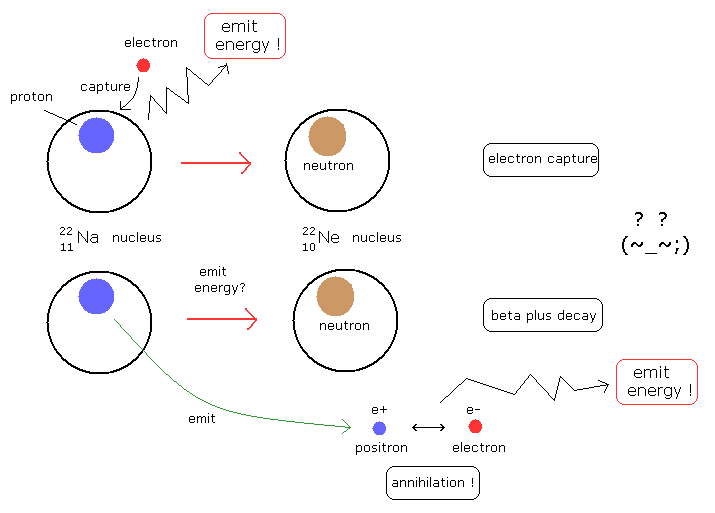
Na (22 11) は 電子捕獲と β+崩壊の両方が起きうるとされている。
電子捕獲では、原子核が 1つの電子を捕獲して 安定な原子核に変化したときに、エネルギーを放出する。
しかし、ベータプラス崩壊においては、原子核が 安定なものに変化しても まだエネルギーを放出しない。そのかわり 陽電子を放出する。
そして、陽電子が どこか別の場所で 電子に出会うと 両者は消滅して エネルギーを放出する。
( つまり β+ 崩壊では 核のエネルギーの一部が 外部の電子に "テレポート"してしまったのか? )
よって これら2つの反応は 同じ原子核を生成するにも関わらず、エネルギーが放出される場所に関して 自己矛盾を含んでいることになる。
陽電子のβ+崩壊は 実は 電子捕獲であると解釈すれば この矛盾を解決できる。
例えば、陽子が多い原子核で、最終産物と最初の産物のエネルギー差が 2mec2 以下だと β+崩壊は起こらず、電子捕獲のみ起こるとされる。
これらの反応は実は同じものなんじゃないだろうか?
( 陽電子と電子は 運動量をもつため、消滅エネルギーは 2mec2 より大きくなるのが普通である。)
もちろん、これらの原子核は 陽電子を放出した時点で、どこか別のところから飛んでくる電子の質量エネルギー のことまで あらかじめ予期しているわけではない。
(Ap-14) 正のポテンシャルエネルギー (= mc2 ) は 非常に不安定な電子。
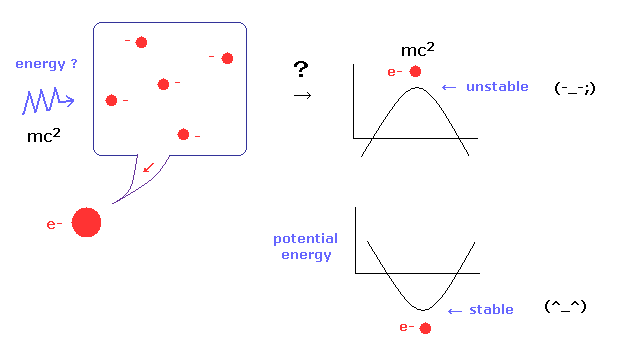
ご存じとおり、電子は 最も安定な素粒子の1つである。
しかし 単一電子のエネルギーが mc2 のように 正 だとすると、電子は 非常に不安定になって 簡単に壊れてしまうことになる。
なぜなら 安定な状態は そのポテンシャルエネルギーが 負 であることが自然だからである。
そのため 大きな 正 のポテンシャルエネルギー mc2 は 非常に不自然なのである。
たとえ、何らかの球殻状の壁で 電子内部にこの大きなエネルギーを閉じ込めているとしても 状況は同じである。
この球殻は 内部の巨大な力に持ちこたえるため 互いに強固につながっている必要がある。
この強固に繋がった状態が いわゆる安定な負のエネルギー状態であり、結果として 電子全体の トータルのエネルギーが 負のポテンシャルのとき、内部の質量エネルギーを安定に保持できることになる。
よって 安定な電子が存在できる条件が そのエネルギーが負である必要があり、正の値はおかしいといえる。
(Ap-15) 陽電子もしくは 陽子 ?
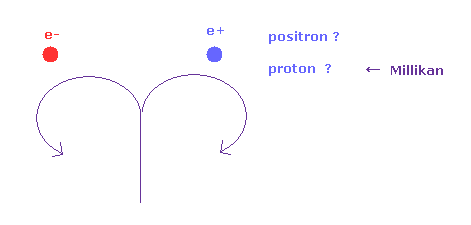
正と負の荷電粒子は 磁場 B の中で 逆方向に回転する。
そのため 彼らは 霧箱内の Ap-15 のケースは 1つは電子で もう1つが陽電子であると主張している。
しかし アンダーソンの師匠であるミリカンは 生涯 この陽電子の存在を 認めなかった。
ミリカンは この陽電子は 単に 陽子か何かであると考えていた。
陽子と電子 (陽電子) が 同じ運動量を持っていても 陽子の質量が重いため 運動量が小さくなる。
そのため 陽子の霧箱内の軌跡は 短く太くなるに違いないと 彼らは主張している。
しかし この解釈は あくまで 陽子の 平均的な行動の話であり、すべての陽子が そうなるとは限らない。
霧箱内には 無限の陽子があるため、そのうちのいくつかは 期待値よりも長い軌跡になってもおかしくない。特に高エネルギー状態の陽子では。
そもそも 粒子同士の衝突の確率は ランダムである。
高エネルギーのミューオン (= 電子 )や 陽子は なかなか 他の荷電粒子と 相互作用しにくいという可能性もある。
(Ap-16) 回転半径。
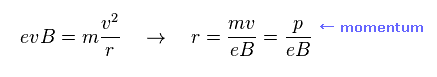
Ap-16 に示したように、荷電粒子の回転半径は その質量でなく 運動量で決まる。
( つまり 電子に容易に崩壊する 役に立たない "ミューオン" は 高エネルギー状態の 電子 の一種と考えると しっくりくる。 )
また 通常の加速器では 陽子と陽電子を見分けることが できず、かつ その速度 ( c 近い ) を測ることもできない。
彼らは あるシャワー崩壊パターンで それらの存在を見分けようとしているにすぎない。
(Ap-17) 反粒子は どのように粒子を区別して くっつくのか?
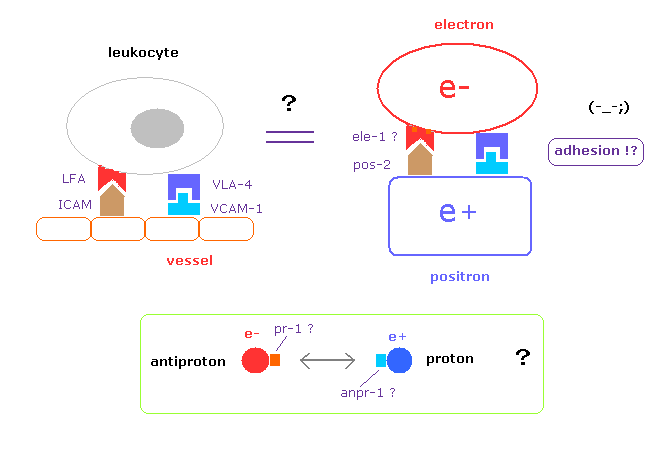
本当の科学の分野においては、例えば 白血球が血管に くっつき得ると分かった瞬間に どのような接着因子 ( LFA, ICAM-1 ) が そこに関わっているか調べるのが 自然の成り行きである。
しかし 彼らは 電子-陽電子間 もしくは 陽子-反陽子間 の 特異的な接着因子に関して 決して調べようとしない。
陽電子が発見されてから すでに 80 年もの歳月が経過しているにも関わらずだ。
このページに示したように、不安定な反粒子は 電子、陽子、中性子捕獲に自然に置き換えることが可能である。
また 非常に安定な電子のエネルギーが マイナスでなく プラス (= mc2 ) であることは不自然である。
これほど長期間にわたって 基本的な"質問をしない" ことは 彼らが これらの概念が 単なる 数学上の産物であると認めていることに等しい。

2013/10/9 updated This site is link free.