トップページ (正確な新ボーア模型)
電子スピンは実在しない。
特殊相対論は間違っている。
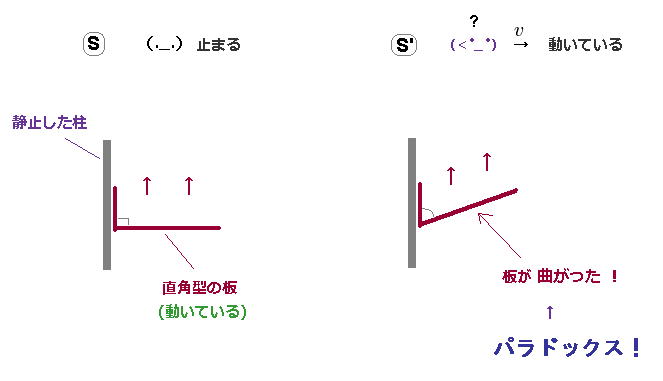
(Fig.1) 直角型の板が 観測者の運動のみで曲がってしまう? ← パラドックス!

Fig.1 では、 直角型の板 (= 茶色 ) が 静止した柱に沿って 一定の速度で 上方向へ動いている。
これらの板と柱は 剛体のため、観測者の運動のみで 折り曲がることはない。
S 慣性系において、観測者は 柱に対して静止している。
S' 系では、観測者は S 系に対して 右方向へ運動している。
驚くことに、S' 系でのみ この直角型の板は 剛体にも関わらず 折れ曲がっているのである。
これは 明らかに 特殊相対論におけるパラドックスである。
(Fig.2) ローレンツ変換。

このページ や このサイトにあるように 特殊相対論においては 観測者の単純移動のみで Fig.2 のように 時間と空間の座標が変換する。
S' 系における 時間 (= t' ) は S 系における時間 (= t ) と x 座標 (= x ) に応じて変化することになる。
この相対論における奇妙な定義によって これから説明する 致命的なパラドックスが 引き起こされることになる。
(Fig.3) S 系における 同時刻の事象は S'系では 異なった時刻に起こる。
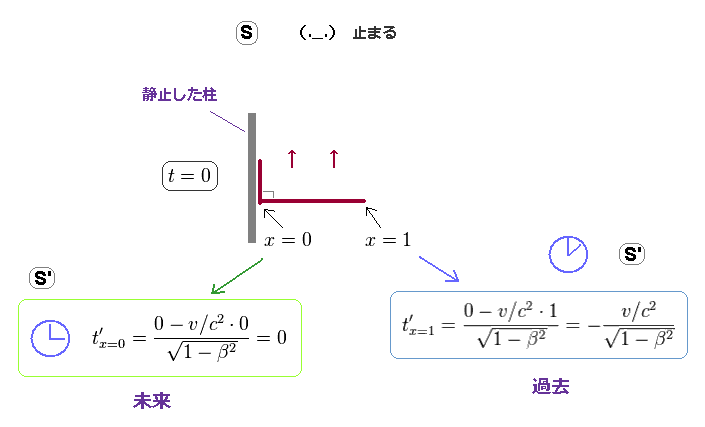
S 系における 時間 t = 0 と 各 x-座標を Fig.2 の式に代入すると、異なった x 座標における時間が S' 系においては 異なったものになることが分かる。
Fig.3 に示したように x = 1 における時間 (= t' ) は x = 0 の地点における時間よりも 早くなってしまう。S 系においては それらの時間は 同時である ( t = 0 ) にも関わらずだ。
この 奇妙な世界こそが 特殊相対論の正体である。
(Fig.4) "剛体の"板が S' 系でのみ曲がってしまう! ← パラドックス。
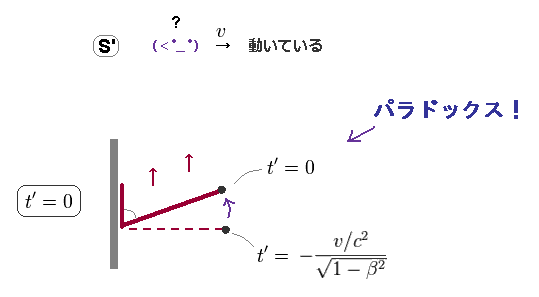
Fig.4 は S' 系の 時刻 t' = 0 において この剛体の板が どう見えるかを示したものである。
上で述べたように、Fig.3 の状態は S' 系のおける異なった時刻のイベントの集合体と言える。
そのため、それらの時刻を 同時刻 ( 例えば t' = 0 ) に揃える必要がでてくる。
時間が経過するほど、この板は 上方向へ進むことを考慮する。
結果的に S' 系では、この直角型の板は 折れ曲がってしまい、直角では なくなってしまう。
この板が 剛体であることを考慮すれば、この "曲がった"状態は 明らかに パラドックスである。
(Fig.5) "V 字型" ( 直角でない ) プレートが この板にフィットする?

ここに "V 字型" の 剛体のプレートがあり、この 曲がった板に ちょうど形がフィットすると仮定する。
時刻 t'=0 に、この V 字型プレートが 折り曲がった板にはめ込まれるとする。
もちろん、この "V 字型" のプレートは 直角型ではない。
(Fig.6) しかし この V 字型プレートは S 系では 直角型の板にフィットしない。

Fig.5 の状態は S 系ではどのように見えるのだろうか?
S 系では、Fig.6 左に示すように、この V 字型のプレートの 左サイドのみが 最初に 直角型の板に はめこまれる。
すこし時間がたって ( t > 0 ), プレートの 右サイドが 板にはめこまれることになる。
しかし この板とプレートは 両方とも 剛体であるため、S 系では 互いに フィットしないことになってしまう。
Fig.6 の右下に示すように、このプレートが 直角型の板にぴったり接するには 板が 壊れる必要がある。
もちろん、そんなことは 不可能である。
(Fig.7) "V 字型" は 両慣性系で 直角にはなれない。

もちろん、このプレートが ある1つの慣性系で V 字型だとしたら、他の慣性系においても 直角型に変化することは 不可能である。
結果的に 特殊相対論の 同時性に関して 致命的なパラドックスが 発生することになる。
(Fig.8) 長い針金のついた箱が ベルトコンベヤーに沿って動いている。
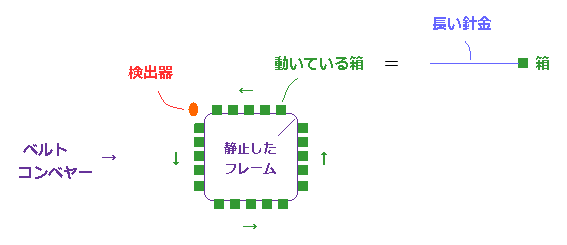
ここで ベルトコンベヤーにおける 致命的なパラドックスについて説明する。
Fig.8 では、内側にある 金属製のフレームは静止している。
この金属製のフレームの周囲に沿って 箱 (= 緑 ) を載せたベルトコンベヤーが 反時計方向へ
動いている。
各箱は 水平方向に 長い剛体性の針金 (= 青 ) を伸ばしている。
この機械の左上部に それを貫く針金の数をカウントする 検出器 (= 赤 ) が設置されている。
(Fig.9) 検出器と各箱についた針金の関係。

各針金は 必ず水平方向を向いているとする。
Fig.9 に示したように、各箱が 機械の上部分に沿って進んでいるとき のみ、検出器が それを貫く針金を検出できるとする。
(Fig.10) K 慣性系は この装置に対して 静止している。
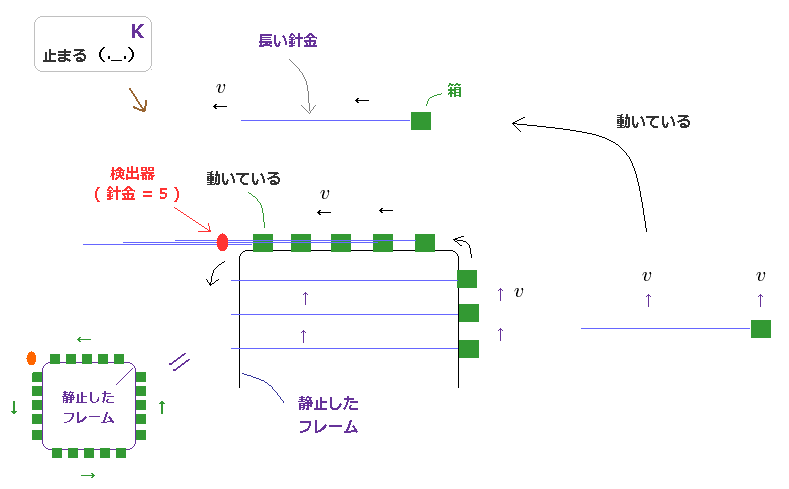
K 慣性系における観測者は この装置に対して 静止している。
K 系では、ベルトコンベヤーが 速度 "v" で 内側のフレームに沿って 反時計方向に動いている。
この装置の各サイドは 必ず 5つのボックスを含んでいるとする。
つまり 検出される針金の数は 必ず K 系では "5つ" になる。
(Fig.11) 動く観測者 (= K' ) から見ると 検出される針金は "3つ" !? ← パラドックス!

K' 系における観測者は この装置に対して 左方向へ 速度 "v" で運動している。
この K' 系では、検出される針金は "5" から "3" へ 減少してしまう。
これは 明らかに特殊相対論における 致命的なパラドックスである。
なぜなら 単純な観測者の移動によって 検出数が "5" から "3" に 減少してしまうからである。
(Fig.12) K と K' 系では 各物体の長さの収縮状態は 異なる。
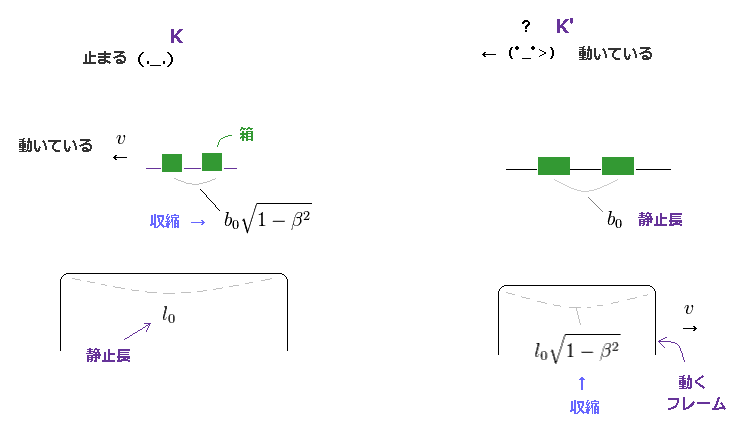
ローレンツ収縮によれば、動いている物体は その進行方向に 収縮する。
K 系では、箱を乗せているベルトは 動いているため、それらは 水平方向に ローレンツ収縮 ( < b0 ) する。
一方で K' 系では、内側のフレームが 右方向へ 動いており、上部にある 箱を載せたベルトが 静止していることになる。
そのため、 K' では、箱付きの各ベルトが その静止長 (= b0 ) に戻る ことになる。
また 内側の金属製のフレームが K' 系において 収縮 ( < l0 ) することになる。
結果的に この装置の K' 系で収縮した上部分には たった"3つ" の箱しか含まれないことになる。K には "5つ" 含まれているにも関わらずである。
(Fig.13) K と K' 慣性系におけるローレンツ変換。

K' 系は 速度 v で K 系に対して左方向へ 動いている。
そのため K と K' 系間のローレンツ変換は Fig.13 のようになる。
( t, x, y, z ) は K 系における 時間と空間座標であり、 ( t', x', y', z' ) は K' 系における 時間と空間座標である。
Fig.2 のローレンツ変換の "v" を "-v" に変えたものである。
(Fig.14) K 系で "5つ" の箱、K' 系で "3つ" の箱 ← パラドックス!

ここで Fgi.13 のローレンツ変換を用いて 各時間と空間の値を 実際に計算してみる。
Fig.14 左には、t = 0 の時間における 各 x 座標 ( x = 0, 3, 5 ) を 示している。
Fig.3 で述べたように、Fig.14 左の状態は、K' 系における 異なった時間のシーンを 集合させたものである。
そのため K' の状態を再現するには K' の中でのある同じ時刻 ( 例えば、 t' = 0 ) を 選ぶ必要がある。
(Fig.15) K' 系での 各時間と空間の計算。
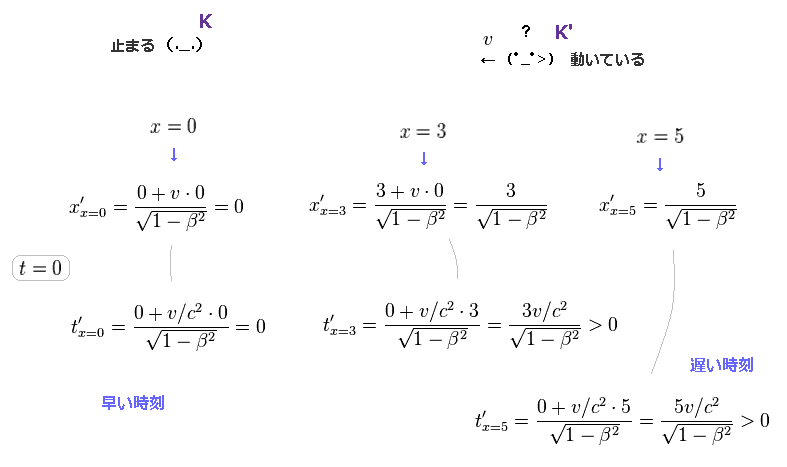
各 x 座標 x = 0, 3, 5 と t = 0 を Fig.13 のローレンツ変換の式に代入して、 K' 系での それに相当する各時間と場所の値が得られる。
Fig.15 と Fig.16 に示したように、 左サイド ( x = 0 ) における時刻 (= t' ) は 右サイド ( x = 5 ) よりも早い時刻を指し示すことになる。
(Fig.16) x = 0 における t' は x = 5 での t' よりも早い。

つまり K 系での Fig.14 左の状態は K' 系での異なった時刻における 集合状態と言える。
K' の観測者から どう見えるのかを知るには 各 t' の時間を 同じもの ( 例えば、 t' = 0 ) に 揃える必要がでてくる。
(Fig.17) K' 系の t' = 0 に ベルトコンベヤーを見ると・・・。
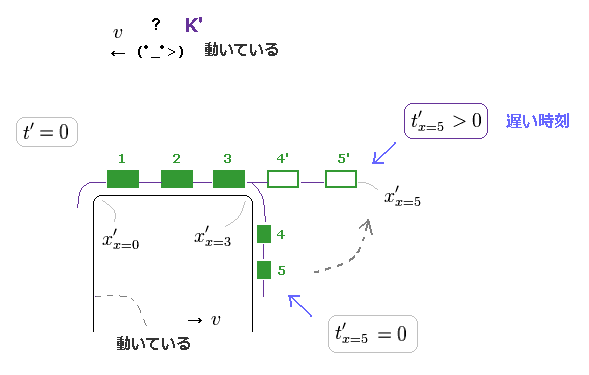
Fig.12 で述べたように、K' 系では 内側の金属のフレームはローレンツ収縮しており ( < l0 )、一方 各ベルトは その元の静止長 (= b0 ) に戻る。
つまり "3つ" の箱のみしか この装置の収縮した上部分に載せることができない。
t' > 0 では、 "4" と "5" の箱は Fig.17 に示すように 装置の上部に位置している。
つまり これよりも早い時刻 ( t' = 0 ) には、これら2つの余分の箱は 内側の装置の右横サイドに 垂直に配列していることになる。
(Fig.18) 剛体性の針金が K' 系 でのみで 曲がる !?
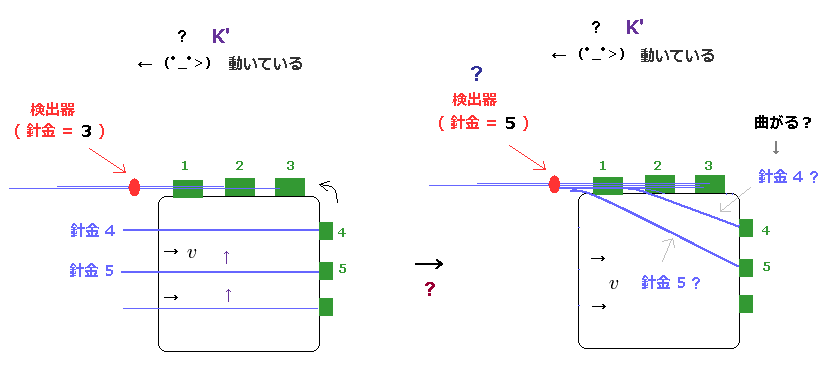
もし特殊相対論が正しいとすると、Fig.18 右のような あり得ない状況を受け入れる必要性がでてくる。
Fig.16 で述べたように、異なった x 座標の地点での K' における時刻は バラバラである。
すべての箱と針金の 同時刻 ( t' = 0 ) における状態を再現しようとすると、どうしても 長い針金が 不自然に 折れ曲がってしまうことになる。
この長い針金の 左部分 (= 4 もしくは 5 ) は 水平方向に沿って 真っ直ぐに伸びている。
しかし 同じ針金における右サイド部分は Fig.18 右に示したように 複雑に 折れ曲がることになってしまう。
(Fig.19) 検出数におけるパラドックス回避のために 剛体性の針金が曲がる?
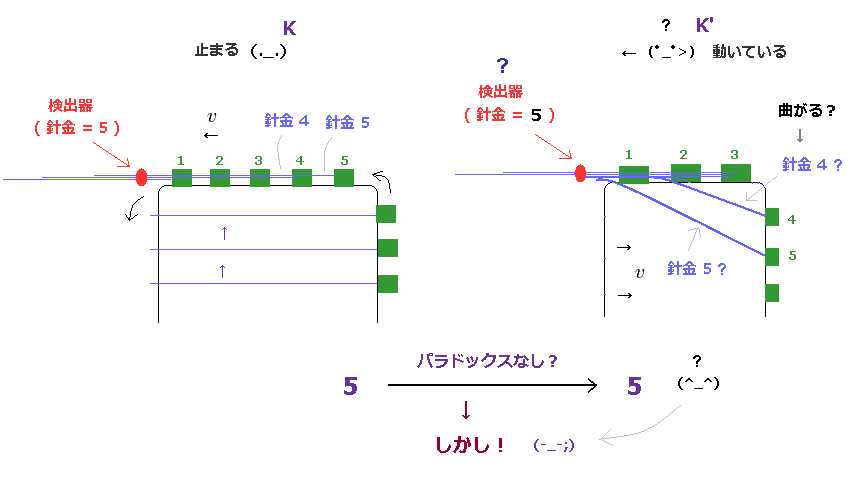
もし この 剛体性の長い針金が 相対論の時間 t' の法則に純粋に従って 折れ曲がることができるとしたら、この系は 異なった検出数 ( 5 ← 3 ) における パラドックスを回避することができる。
しかしもちろんのこと、針金と箱は 剛体性であるため 常に一様に同じ状態を保つ必要があるため、こんなことは不可能である。
よって 特殊相対論による この折れ曲がった針金の現象は 非常に不自然で 現実的には起こり得ないものであることが分かる。
(Fig.20) 剛体性の長い針金が 便利に折れ曲がる? すなわち 相対論は間違い。
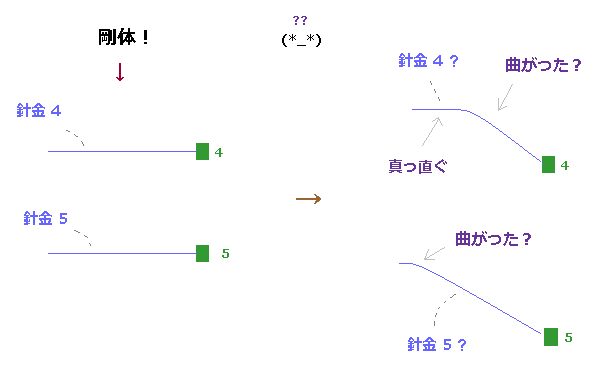
もし 特殊相対論が正しいとすると、この針金の 左部分は 水平方向に 真っ直ぐになり、同一の針金の 中ほどの部分のみ、複雑に 折れ曲がることになる。
同一の針金のすべての部分は 運動の方向などの点で 同一の種類のものであるため、このように 場所に応じて 便利に折れ曲がることは あり得ないことであることが分かる。
これはつまり 特殊相対論は 間違いであることを示している。
(F-1) K 系における 針金つきの箱 4 の運動。

ここで 特殊相対論によって生じる 不合理な現象について説明する。
F-1 では、 K 系の観測者が 箱 4 と その針金の動きを見ている。
(F-2) 剛体性の針金が 観測者の単純移動のみで "折れ曲がる" !?

Fig.19 で述べたように、 この 剛体性の針金は K' の観測者からの視点では 折り曲がってしまう。
もちろん、この現実の世界では こんなことは 起きるはずもないため、特殊相対論は その中に 致命的な欠陥を含んでいることになる。
K' 系での同時刻で起こったイベントの中で、左方向の場所が K 系での 未来の事象を映していることになる。
そして 右方向に行くほど 過去の事象を映している。
(F-3) 触れずして 針金の "未来の"状態を 変更できる !? ← パラドックス!
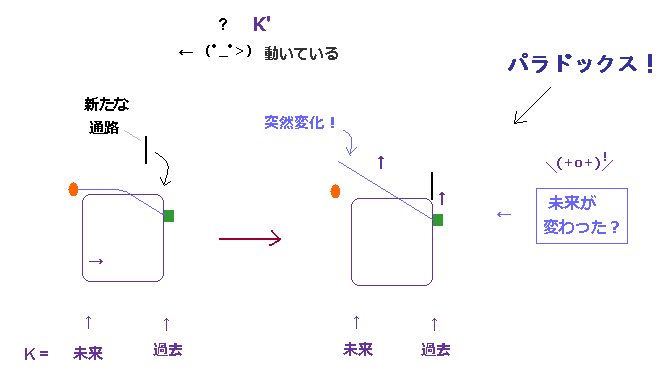
驚くことに、もし自然界が特殊相対論に従っているとしたら、触れずして 針金の未来の状態を変更できることになってしまう。
F-3 では、急きょ 新たな通路を 挿入して これにより 箱がその後 上方向 ( 検出器の方向でなく ) へ移動するようにした。
この箱は 新たな通路には まだ到達していないため、もちろん この通路の行先も 知らないはずである。
これにも関わらず この針金の 左サイドの部分は この通路による未来の影響を察知して 左上方向へ 真っ直ぐになってしまうことになる。
なぜなら この新たな通路を入れたことにより、この箱は後々 検出器の方向へ曲がることなく、上方向へそのまま進むことになるからである。
これはつまり、私達は この針金に触れずして その左サイドの部分 (= K 系での未来 ) の状態を変えてしまう超能力を保持していることになる。
もちろんそのようなことは不可能なため、相対論的な世界が 非実在的で間違いであることが分かる。
------------------------------------------------------------------------
(F-4) 異なった場所に同時に力を加えると 長い剛体が 同時に動きだす。
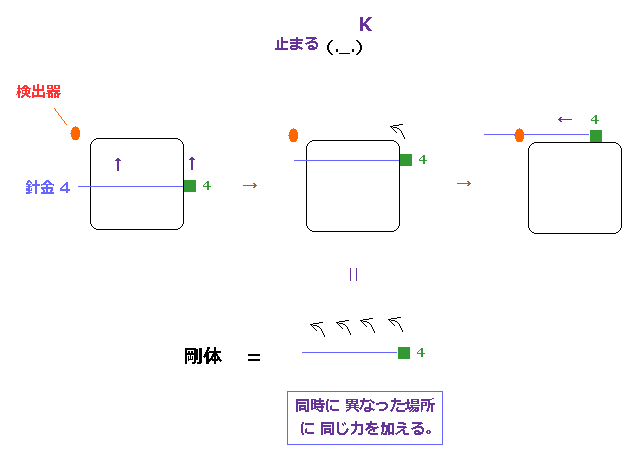
基本的に 力の伝達速度は 最高速度の光速 c を 順守する必要がある。 ( "超光速" は 不可能である。 )
すなわち、何か 剛体性の長い物体全体を 同時に 加速させようとしたとき、
F-4 に示したように、同じ力を この物体の異なった場所に 同時に加える必要がある。
もし 物体中の ある1点のみに力を加えた場合、剛体全体が加速し始めるまでに いくらか時間 (= 全長 / 光速 ) がかかることになる。
異なった場所に加える力の数を増やせば増やすほど、それだけ 加速し始めるのに要する時間が 減少することになる。
すべてが同時に動きだせば、もちろん、この物体の長さや形は いかなる地点においても 変化することがないため、剛体であることのルールが守られる。
(F-5) 剛体性の通路を挿入すると、他の小さな力は無効になり、針金全体が上方向へ進む。
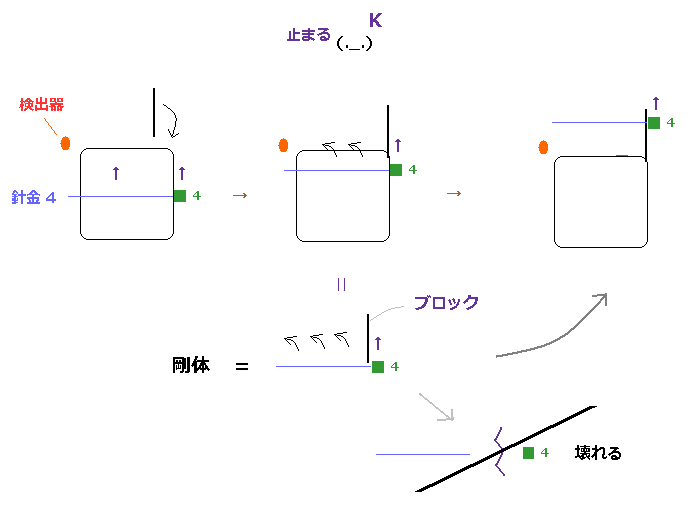
剛体の内部では 長い針金のすべての部分が 局所のポテンシャルエネルギーを介して 隣の部分と 強力にくっついている。
そのため 剛体内部では いかなる部分のおいても 伸ばしたり、壊れたりすることができない。
そのため、F-3 や F-5 のように 突如として 新たな通路を挿入すると、この剛体性の針金を 左方向へ 加速することができなくなる。
つまり たった1つでも 強力な障害物 ( この通路など ) があれば、これによって この剛体性の針金全体の 進行方向に 影響を与えることになる。
例えば、この針金の左部分のみ 左方向へ進み、残りが上方向に進むと この境界部分が 伸びてしまい、剛体だとしたら、この伸びには 局所の強力なポテンシャルエネルギーを打ち破るくらいの力を両側に加えなければ不可能である。
ようするに 剛体をある方向へ加速させようとするとき、いかなる障害物も取り除く必要がある。
もし 何らかの強力な抵抗物が1つでも残ると、他のすべての小さな力は無効になる。
結果的に、特殊相対論が正しいとすると、F-3 のような 新たな通路の挿入によって、未来が変化するといった奇妙な現象が起きるため、間違いであることが証明できる。
------------------------------------------------------------------------
(Fig.21) 電荷と電流のパラドックスも同じパターンである。
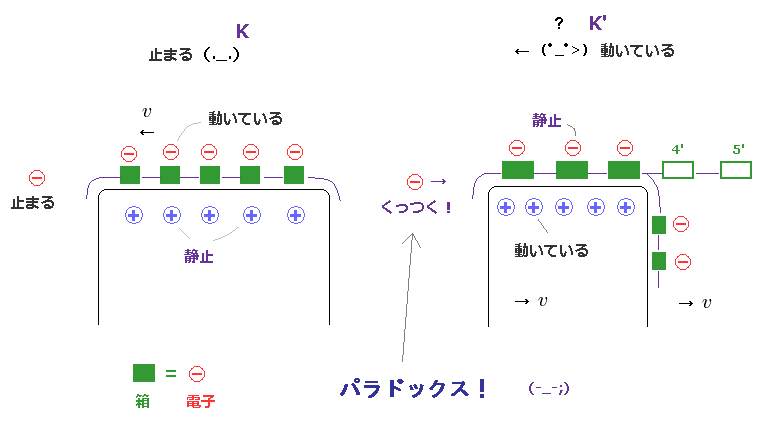
このページ や このページにあるように、特殊相対論は 電磁気学で 破綻している。
この電磁気におけるパラドックスも 上記のベルトコンベヤーと長い針金のパターンと
同じ である。
運動する箱を 負電荷の電流と見なすことができる。
そして フレームの各サイドには それと同じ量の正電荷を含んでいる。
(Fig.22) 負電荷が "5" から "3" に減少する。 ← パラドックス。
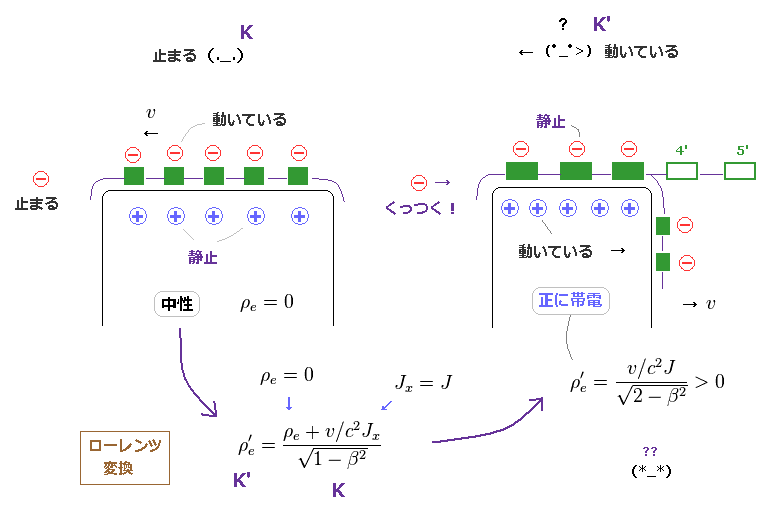
このページに示したように、 電荷密度 (= ρ ) と 電流 (= J ) を用いて、 上サイドの電流が K 系での中性から K' 系での 正電荷に変わってしまうことが分かる。
電流のループは 2つの方向 (= 水平と垂直方向 ) を含んでいる。
相対論的な電磁気学では 2つの異なる方向を コントロールできない。
Fig.22 左では、外部の負電荷が K 系では 静止しているが、K' 系では 電流方向へ引きよせられてしまうことになる。
なぜなら K 系では 電線は中性だが、K' 系では 正電荷を帯びてしまうからである。
これは 明らかに 致命的なパラドックスであり、すなわち 特殊相対論が間違いであることの証拠である。
(Fig.23) 特殊相対論が間違い → 一般相対論も間違い。架空の理論だらけ。
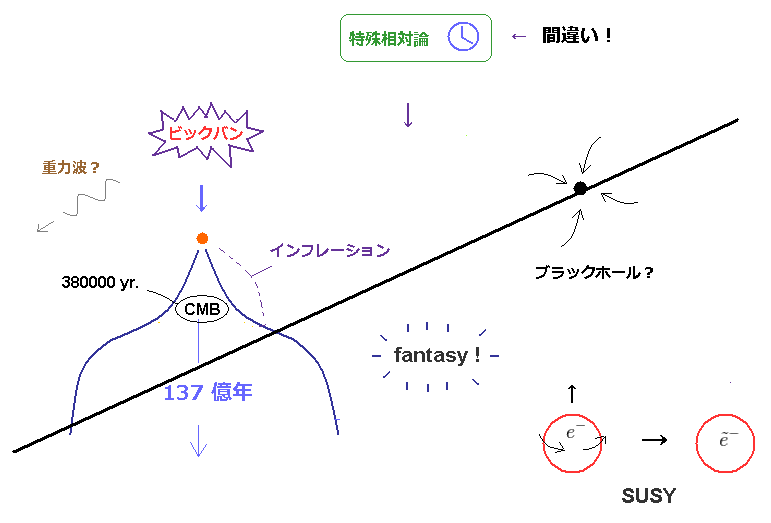
一般相対論は その一部として 特殊相対論の慣性系も内包しているため。特殊相対論が 間違いだと、当然、一般相対論も 間違いということになる。
結果的に 宇宙インフレーション、 ブラックホール、 超対称性理論などは すべて 間違いということになる。
なぜなら これらの理論はすべて 相対論を基にしているからである。
実際のところ、初期宇宙や ブラックホールなどの 架空の概念の研究を 私達が いくら続けたとしても、科学、社会生活の発展や進化などに 何の貢献も なされないことが分かる。
要するに 現在 世界中の科学者達が これらのフィクションのために 多大な貴重な時間を無駄に浪費し続けているのである。
これら 超対称性粒子や 10 次元の超弦理論などは 直接観測することも不可能であり、永久に 私達の生活に 役立つことがないことは誰もが認めるところである。
要するに これらの理論は まったく非実在的な概念であると言っても何の代わりもないのである。
(Fig.24) 2つの力 Fy が 釣り合っている。

このページでは、ニュートン力学上の力のローレンツ変換によって 致命的なパラドックスが生じることを示した。
上記の電磁気学や ベルトコンベヤーのパラドックスは ローレンツ変換そのものに起因するものである。
一方、この力の変換におけるパラドックスは 相対論的な運動量とエネルギーという概念を新たに導入したことによって 生じるため、上記のパラドックスとは原理的に 独立している。
Fig.24 では、2つの等しい力 Fy が K 系 (= 観測者は静止 ) において 静止したレバーに加えられている。
このレバーは 支点の両側に等しい長さの腕を持ち、K 系においては ちょうど釣り合って動かない。
これらの力の1つ (= Fig.24 左 ) は 静止しており、もう1つの力は x 方向へ 速度 "v" で 動いている。
(Fig.25) レバーは 動く観測者の視点 (= K' ) でのみ 回転する?
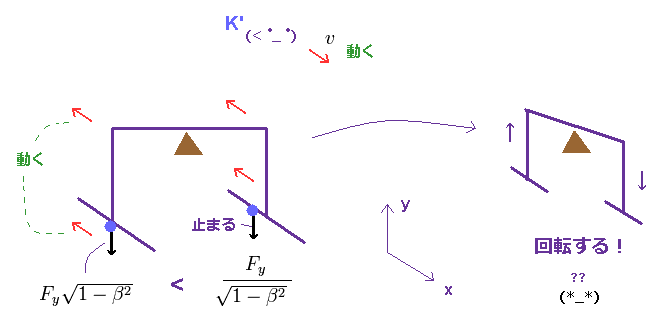
観測者が x 方向へ 速度 "v" で動きだすと、このレバーと左側の力は 逆方向へ
動きだすことになる。
結果、この力 (= Fig.25 左 ) は 特殊相対論によれば 減少することになる。
一方で、右の力は K' 系においては 逆に 静止しているため、観測者の動きによって 増加してしまう。
結果、このレバーは K' 系でのみ 時計方向に 回転してしまうことになる。
この理不尽な 力 Fy の変換は 直角レバーのパラドックスの原因の1つである。
もちろん、このパラドックスには 解決策は 何もなく、よって 相対論的なエネルギー、運動量の概念が 間違いであることを示している。
(Fig.26) 2つの人工衛星における ふたごのパラドックス。

ローレンツ変換に示されたように、1つの慣性系における各時間と空間は 違う慣性系のそれと 1 : 1 で独立に対応している。
そのため、同じ場所で 異なった時間というような 双子のパラドックスを 特殊相対論のみで証明することは 不可能であることが分かる。
双子のパラドックスを証明するには 一般相対論の力を借りなければできない。
なぜなら 一般相対論は 中心方向への重力などという 異なる種類の概念を採用しているからである。
このページに示したように、2つの同一の衛星が 地球周囲の同じ軌道上を反対方向へ周回しているとき、これらの時計は 双子のパラドックスを示すことになる。
1つの人工衛星 (= A ) から見ると、他の人工衛星 (= B ) の時計は ゆっくり動いている。
しかし "B" の人工衛星から見ると、 "A" の人工衛星の時計のほうが ゆっくり動いていることになる。
ではいったい どっちの時計がゆっくり動いているのだろうか?
一般相対論では これら2つの人工衛星を 重力の力を用いて 互いに再会させることが可能である。
つまり 双子のパラドックスは 一般相対論の助けを借りて 初めて 表に露呈することになる。
(Fig.27) S' 系でのみ 負電荷が 引き付けられる?
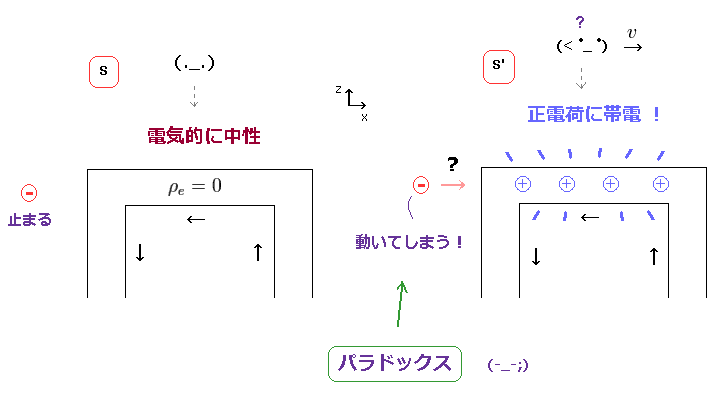
このページで、上部 (下部) の電線に含まれる 電荷密度が 観測者の単純移動のみで変化することを示した。
このセクションでは、異なった慣性系における電荷と電場の変換について振り返って補足することにする。
(Eq.1) 電荷密度 (= ρ ) と 電流 (= J ) の間の普遍的な関係。
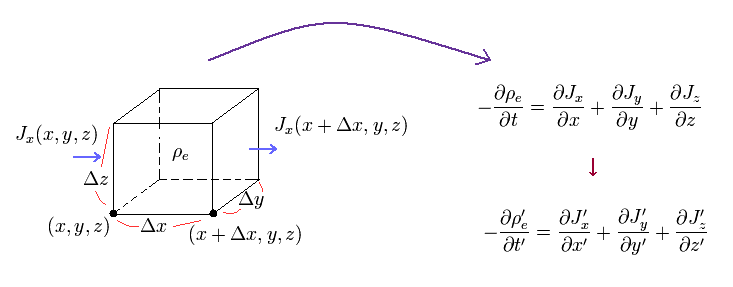
このページに示したように すべての慣性系において、電荷密度 (= ρ ) の増減は 電流密度 (= J ) の変化と等しくなる必要がある。
なぜなら "電荷" が 突如として どこかで消失するなどということは どの慣性系でも
あり得ないからである。
(Eq.2) 電荷密度 (= ρ ) と 電流 (= J ) のローレンツ変換。

Eq.1 の関係を満たすには、電荷密度 (= ρ ) と 電流密度 (= J ) は ローレンツ変換の元で Eq.2 のように変換しなければならない。
コンマ ' は S' 系の意味であり、この系は S 系に対して 速度 v で x 方向へ動いている。
(Fig.28) S と S' 系で Q = Q' を満たす。
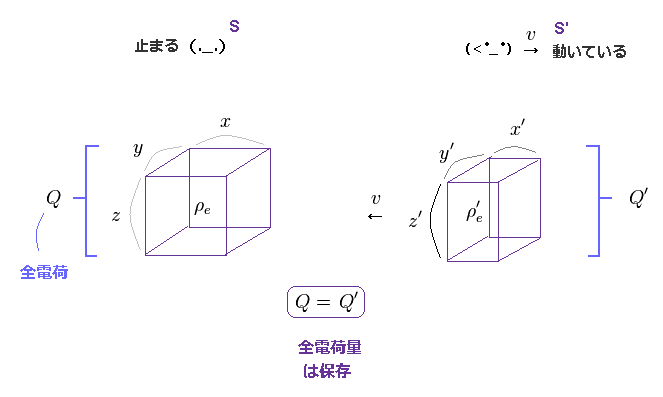
Eq.2 のローレンツ変換を用いて、全電荷量 Q は 異なった慣性系においても 保存することが分かる。
Fig.28 左では、電荷密度 (= ρ ) の立方体が S 系で静止している。
この立方体の 縦、横、高さは x, y, z とする。
(Fig.29)
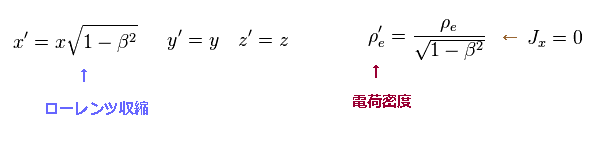
観測者が 速度 v で x 方向へ動いている S' 系から見ると、
移動方向の長さ (= x' ) のみが ローレンツ収縮している。
Eq.2 を用いると、Fig.29 に示すように、 電荷密度 (= ρ' ) は 増加する。
(Fig.30) 全電荷量 Q は 変化しない。

全電荷量 Q は 電荷密度 (= ρ ) × 体積 (= xyz ) で与えられる。
Fig.29 から、この Q の値は S' 系でも変化しない ( Q = Q' ) ことが分かる。
つまり 電子や陽子の全電荷 "e" も観測者の運動によらない定数になる。
(Fig.31) ガウスの法則と 電場 Ex の変換。

ある電荷が 面 S で囲まれているとき、この全電荷量は S 全体を貫く電場の面積分に等しい。
特殊相対論によれば、電場 E と 力 F の移動方向の成分
( この場合 Ex ) は ローレンツ変換によって 変化しない。
Fig.31 では、外電荷 (= + ) に作用する電場と力の間に矛盾はない。
これらは 異なった慣性系においても変化しないからである。
Fig.30 と Fig.31 から、電荷が動いているときも ガウスの法則が有効であることが分かる。
(Eq.3) 電磁場のローレンツ変換。

このサイト や このサイト (p.91) にあるように E, B 場のローレンツ変換は Eq.3 のようになる。
この変換は 相対論とマクスウェル方程式の融合に必須である。
(Fig.32) ローレンツ変換。

Fig.32 のローレンツ変換を用いて、y と z 方向でも ガウスの法則が有効であることを示せる。
Fig.33 に示したように、x-y 平面における 電荷密度 (= ρ ) は S' 系で増加する。
(Fig.33) ガウスの法則は S、 S' 系で有効である。
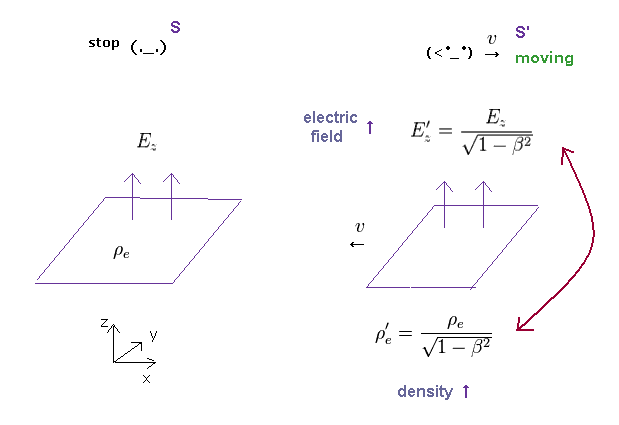
電荷密度における増加に 比例して、電場 Ez ( もしくは Ey ) も増加する。
結果的に 電場の面積分は いかなる慣性系においても内包する電荷量に等しくなる (= ガウスの法則 )。
(Fig.34) 異なった面積分においても 同じ電荷量 Q を与える。
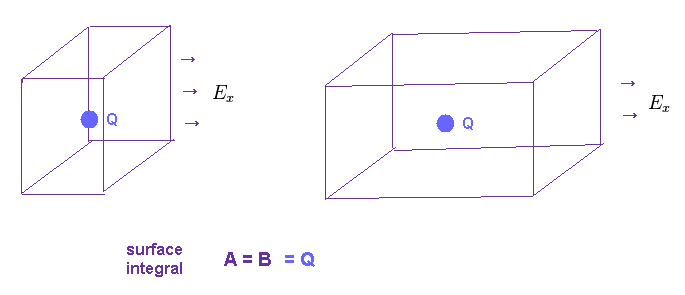
もちろん、全電荷量が等しいとき、それを囲む 異なった形の面を貫く電場の面積分においても 同じ電荷量を与える必要がある。
もし 同じ電荷を囲んでいるにも関わらず Ex や Ey の変化量が異なると、面積分の値も 違ってきてしまう。
( Fig.34 の左右の異なる形の直方体の面積分で 異なった値を与えてしまうことになる。 )
(Fig.35)
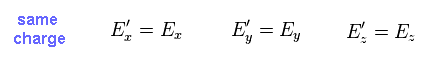
そのため 包み込む電荷量が同じとき、すべての方向の電場も ローレンツ変換によって変化してはいけないことになる。
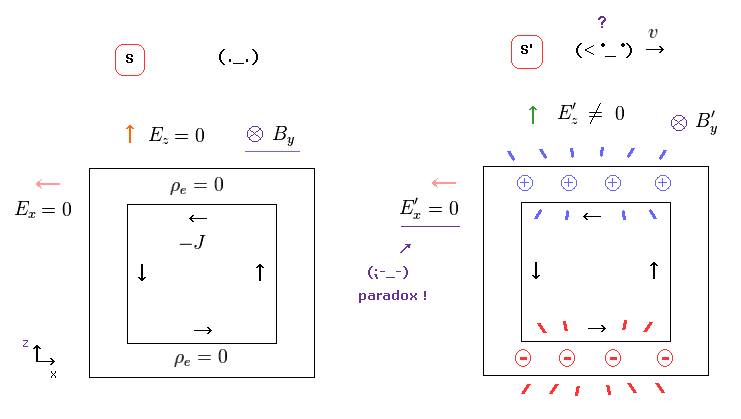
そして Fig.27 や Fig.36 のような 致命的なパラドックスが出現してしまう。
(Fig.36) 電場 E'x はゼロだが、 E'z は ゼロでない。 ← パラドックス ! おかしな電荷達。

2014/7/23 updated This site is link free.