
トップページ ( 正確な新ボーア模型 )
電子スピンは存在しない。
QED ラムシフトは 非常に 疑わしい。
(Fig.1) 電子スピンと原子核スピン間の 相互作用?

水素原子の 超微細構造 は このサイトにあるように 電子スピン (= 1s ) と 原子核スピンとの相互作用によって生じるとされていて 非常に小さい。
しかし 量子力学による説明は あまりにも 現実離れしすぎている と言わざるを得ない。
量子力学によれば、シュレディンガーの水素原子の 1s 軌道にある電子は 常に 陽子 (= 原子核 ) を貫通していることになっている。
なぜなら "s" 軌道の角運動量は ゼロ ( L = 0 ) だからである。
驚くことに、この電子が 小さな陽子の内部に 存在するときのみ 超微細構造の磁気相互作用 (= 5.9 × 10-6 eV ) が 起きる ということになっている。
常識的に考えて、これほど 小さな磁気相互作用が 陽子の内部という強力な力が働く状況下でも、 正確さを 常に保てること自体 あり得ないことである。
(Fig.2) QED は 実験結果と矛盾する。

このサイトにあるように、最近の実験結果では 量子電磁気学 ( QED ) による予測値が 実験結果と 違うことが 明らかになった。 ( 陽子の半径 QED -- 0.877 fm, vs. 実験結果 -- 0.841 fm. )
基本的に 原子核 (= 陽子 ) の 電気的、磁気的分布の詳細を 理論のみから 知ることはできない。
実験結果によるデータが 必要不可欠である。 つまり QED 自体 第一原理ではないのである。
QED は ラムシフト ( ? ) の実験データ と その予測値間の食い違いから 陽子の大きさを 推定しているにすぎない。
つまり、 様々な ニュースサイトは 量子電磁気学に関して 大幅に "誇張" して 宣伝しているということになる。
さらに、原子核の磁気分布は Bohr-Weisskopf 補正にあるように、まったく予測不能で QED などに不確定性を与える要因となっている。 このサイトなど参照のこと。
(Fig.3) フェルミ接触相互作用が 微細構造の主要要因。

超微細構造を引き起こす主要な要因が フェルミ接触相互作用 と言われている。
重要な点は このフェルミ接触の値には 何の正当な物理的理由が 存在しない ということである。
Fig.3 では、 μe と μp は それぞれ 電子 と 陽子の 磁気モーメントである。
確率密度波 ψ(0) は 水素の 1s 軌道電子が 陽子の内部に存在するときのみ 陽子と相互作用することを意味している。
この主要なフェルミ項を 実験値に合わせるように 人為的に微調整するときに、 QED をここに追加するにすぎない。 このサイト (p.26) 参照のこと。
つまり、 便利な QED は ごく微量の調整のために利用されていると言える。無限大に発散してしまうのだが・・。
問題は この係数の 8/3 π という値を どのように得たのかと言う点である。
後で説明するが、残念ながら、この値には 何の 納得のいく根拠が
存在しないのである。
(Fig.4) 量子力学は 磁場が 陽子内部にしか 生じないと主張している。

Fig.3 によれば、 彼らは 原点 (= 原子核の位置、 r = 0 ) における電子の確率密度のみ使用している。
これはつまり 磁場は 陽子の内部のみに生成されることを意味している。
もちろん、これは かなり強引な仮定に基づいており、物理的なリアリティーは まったくないと言っていい。
しかし この ψ(0) という係数に頼らない限り、超微細構造の値を得ることができないので 仕方なく採用しているにすぎない。
常識的に考えれば、非常に弱い超微細構造 (= 5.9 × 10-6 eV ) は 陽子内部の 巨大なクーロン力やら 他の強い力などによって 攪乱され 容易に消失してしまうことは 明らかである。
(Fig.5) 電子スピンが陽子内部に入る → スピン速度が 光速を超える。

量子力学によれば、電子全体が 陽子内部に しっかり入り、かつ 陽子の磁場 (= B ) と相互作用することになっている。
しかし このページによれば、電子のスピンの回転速度は 陽子内部では 1644 × 108 m/s (= 光速の 500 倍 ! ) にも達することになる。
つまり、陽子内部の電子によって 超微細構造が引き起こされるという考え自体が 非現実的で あり得ない ことが分かる。
(Fig.6) 原点 (= 原子核 ) における 電子の確率密度は ゼロ。

電子の確率密度は 波動関数 × 半径 (= r ) で 与えられる。
これはつまり 電子の 原点 (= 原子核 ) における確率密度はゼロ になってしまうことになる。
ということは、超微細構造自体 起こり得ないことになってしまう。
( QED の ラムシフトも 不可能である。 )
(Fig.7) 原点 (= 陽子 ) 付近の 磁場が 無限大に発散。

このサイト (p.8) や このページによれば、磁気モーメント (= μp ) によって生じる磁場は r (= 距離 ) の 3乗に 反比例する。
電子が 陽子の近くに近づくと、距離もゼロになっていく ( r → 0 )。
結果的に、磁場 ( エネルギー ) も ± 無限大 に発散することになる。
(Fig.8) 超微細構造における 非現実的な磁場。

このサイト (p.2) にあるように、超微細構造における磁場は ディラックのデルタ関数 (= δ(r) ) を使って表わされている。
つまり、磁場は 原点 (= 原子核 ) で 無限大 に発散することになる。
彼らのロジックによれば、この 無限大の磁場 B が Fig.6 に示した 原点での確率密度ゼロ を ちょうどキャンセルしてくれるということらしい。
なぜなら 原点において、 ∞ (= B ) × 0 (= 確率密度 ) が "有限" の値を与えるからである。
ご覧のとおり、量子力学による超微細構造の考え方は 非常に 強引で 受け入れ難いものである。
(Fig.9) 磁気エネルギーが 原点でのみ ±∞ に発散する !?

デルタ関数に基づく磁場 (= B ) を用いて、超微細構造における 磁気エネルギー分布を知ることができる。
驚くことに、この磁気エネルギーは 原点において ±∞ に発散してしまう。
原点以外のすべての地点では、磁気エネルギーは 必ずゼロ になってしまう。
果たして この電子は 自身の場所に応じて どのように 高エネルギーの光子の吸収、放出を制御しているのだろうか? あり得ない設定である。
(Fig.10) 磁気双極子エネルギーは 陽子内部で 3 × 108 eV にも達する!

陽子の半径 (= 0.8 fm = 0.8 × 10-15 m ) のデータを用いると、陽子内部では 磁気双極子エネルギー ( Fig.7 参照 ) は 3 × 108 eV という 非現実的なくらい巨大な値になる。
非常に小さな超微細構造 (= 5.9 × 10-6 eV ) のエネルギー範囲内で、これほど巨大な磁気エネルギー (= 3 × 108 eV ) が 突如として出現して 電子に吸収、放出されていることは どう考えても無理がある。
(Fig.11) 水素の 1s の波動関数は ボーア半径 (= a0 ) を含む。

このサイト (p.3) にあるように、水素の 1s の波動関数は ボーア半径の3乗の逆数 (= 1/a03 ) の値を含んでいる。
つまり、原点における確率密度の値の中に、このページの古典力学的な模型のような 電子と原子核間の平均距離の情報が 含まれているのである。
これも 量子力学による超微細構造の導出の 重要なトリック である。
(Fig.12) ボーア磁子 (= 電子 ) と 核スピン間の 磁気相互作用。

最初に 原子核スピン (= μp ) と 電子の磁気モーメント (= ボーア磁子 ) 間の 磁気エネルギーを計算してみる。
ボーア磁子 は 元々は ボーアの古典的な原子軌道から導出された。
しかし 偶然にも、電子スピンの磁気モーメントの大きさが このボーア磁子の大きさに 一致してしまったのである。
陽子の磁気モーメントの大きさは 電子スピンと比較して 格段に小さい。
( 陽子の磁気モーメント = 電子の磁気モーメントの 約 1/1000 倍。 このサイト も参照のこと。 )
陽子の有限の半径 (= 0.8 fm ) や 非常に重い質量を考慮すれば、陽子のスピン速度は このページにあるように 光速を 超えない。
(Fig.13)

このページに示したように、古典的な磁気モーメント (= Iπa2 ) によって生じた磁場 (= B ) は Fig.13 のようになる。 磁気モーメントは 面積 × 電流 I で与えられる。
ここでは 電子 (= e- ) は 円形軌道上を運動しており、これによって 電流 I が生じている。
"B" は "p" 地点 における磁場である。
(Fig.14) 電流 I によって生じた磁場。

Fig.13 で z = 0 のとき、原子核 (= e+ ) の地点における磁場 B は Fig.14 のようになる。
すでに述べたように、この磁場の大きさは 距離 (= a0 ) の
3乗 の逆数に比例する。
(Fig.15) ボーア磁子 = 電子の磁気モーメント

"μe" は ボーア磁子で、電子 ( スピン ) の 磁気モーメントに 等しい。
(Fig.16) ボーア半径。
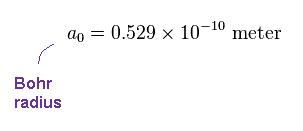
"a0" は ボーア半径 (= 0.529 Å ) であり、水素の基底状態における 平均の半径 である。
(Fig.17) 陽子のスピン磁気モーメント (= μp ) は はるかに小さい。

陽子の磁気モーメント (= μp ) は その非常に重い質量のため 電子に比べて 非常に 小さい (= 1/700 )。
重要な点は 陽子のg因子 (= 5.58 ) の値は 実験値 であり、QED などから得られたものではない。
また ディラック方程式の値 "2" とも異なる。
(Fig.18) 単純な模型による 電子・原子核スピン 相互作用。

Fig.14 - Fig.17 を用いると、 "up" と "down" の原子核スピンと電子間のエネルギー差を知ることができる。
このエネルギー差は 計算すれば 2.2 × 10-6 eV になる。
(Fig.19) 超微細構造。

超微細構造の実験値は 5.9 × 10-6 eV である。
そのため これらの値は ほぼ 同じ次数 ( 〜 10-6 eV ) をもつが、若干違いがある。
(Fig.20) 非常に弱い超微細構造は 他の小さな影響を被りやすい。

陽子の磁気モーメントは 非常に小さい ( 電子の磁気モーメントの 約 1/700 倍 しかない )。
そのため 非常に小さな超微細構造は 原子核の 小さなサイクロトロン運動や 振動などの影響によっても 容易に 変化してしまう。
もともと、陽子自体 電子のクーロン力によって 常に 回転運動していることが知られている (= 換算質量効果 )。
つまり、陽子の回転方向の違いによって 所謂 "マグヌス" 効果などで 小さな エネルギー差が生じても不思議ではない。
(Fig.21) 電子が 陽子内部にあるときのみ、陽子と相互作用できる?

一方で、量子力学による超微細構造は 完全に狂っているとしか言いようがない。
彼らが主張するには、電子は 陽子の内部に 存在するときのみ、陽子と 磁気的に 相互作用できることになっている。
(Fig.22) フェルミ接触項が 主要な要因。

量子力学 や このサイトによれば、フェルミ接触相互作用 (= デルタ関数の部分 ) が 1s の超微細構造を引き起こす 主要な要因 になっているらしい。
(Fig.23) 電流 I によって生じる 磁場 (= B )。

重要な点は このフェルミ接触項 (= 8/3π ) には 何の明確な物理的な意味 というのが
存在しない ということである。
例えば、相対論的な ディラック方程式は すべてのフェルミ粒子に対して g因子 = 2 ( ← 陽子の値と違う) を与えるだけである。
驚くことに、 "電磁気学 ( 上 )" ( J.D. ジャクソン ) によれば、このフェルミ接触定数は 純粋な 古典的電磁気学 によって得られると主張しているのである。 このサイト 参照のこと。 つまり 量子力学的な "スピン" 自体が 幻想だったということか?
このサイトにあるように 円形電流 I の中心に生じる磁場 B は Fig.23 のようになる。
(Fig.24) 陽子の球内に含まれる 全磁場?

次に、Fig.23 の磁場を 陽子の球内 (= 4/3πa3 ) で積分し 全磁場を得る。
この球に関係した "4/3" という値が キーポントである。
結果的に 陽子という球の内部の全磁場が Fig.22 のフェルミ接触項を与えると主張しているわけである。
見てのとおり、この計算は 量子力学でなく 完全に 古典的電磁気学に基づいたものである。
(Fig.25) 他の部分の磁場は すべて打ち消し合う?

基本的に 磁場は "閉殻系" である。
つまり、上方向と下方向の磁場のの大きさは 全空間で同じになる。
もし この陽子球の外部で 全磁場を積分して計算すると、この値は ゼロになることが分かる。
これはつまり、このロジックによれば、"スピン・スピン" 磁気相互作用 ( ex. 三重項、一重項 ) というものが 起こり得ない ことになる。
(Fig.26) ディラックのデルタ関数 (= δ )。

さらに、この全磁場のすべてを 原点 ( r = 0 ) の1点のみに 集中させてしまったことである。
つまり 原点での磁場 (= B ) が 無限大 に発散してしまうことになる。
他の地点では 磁場は存在しないとしている。
もちろん、この状況が実際に起きているとは 到底考えられない。
(Fig.27) 磁場 B は ベクトルポテンシャル A の回転 で与えられる。

このサイトにあるように 磁場 B は ベクトルポテンシャル A の回転 で与えられる。
このベクトルポテンシャルは 古典的な アンペール ( ビオ・サバール ) の法則と一致する。
そして 磁場 B を 陽子の球内で積分する (← トリック )
"R" は 陽子球の 半径 である。
(Fig.28)
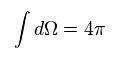
"Ω" は 球座標での 立体角 (= 4π ) である。
(Fig.29) ビオ・サヴァールの法則 = "古典的な" 電磁気学 !?

ここでは 純粋な古典的電磁気学 に基づく ベクトルポテンシャル "A" を用いる。
Fig.29 の関係式から ビオ・サヴァールの法則が導かれる。 このサイト (p.11) も参照のこと。
(Fig.30) 全磁場。

Fig.27 - Fig.29 を用いて 複雑な計算をした後、Fig.30 の関係式を得る。
重要な点は この方法は 陽子が 純粋な球 であるという前提条件に依存している ということである。
(Fig.31) 陽子の 磁気モーメント μp

磁気モーメント μ は 面積 × 電流 で与えられる。
Fig.31 の積分は 陽子内部の 全磁気モーメント を与える。
(Fig.32) 全磁場 → フェルミ接触相互作用?

Fig.30 と Fig.31 から、Fig.32 の全磁場を得ることができる。
そして、この得た全磁場 B を ディラックのデルタ関数を用いて r = 0 の原点に 一極
集中させてしまう。
これも 人為的な トリック の1つである。
結果的に Fig.22 のフェルミ接触項を得ることができた。
(Fig.33) 小さな電子のスピン速度は 光速を はるかに超える !?

このように フェルミ接触項を 純粋な 古典電磁気学 (= 円形電流 + ビオ・サヴァール ) によって得た。
もし 古典的な電磁気学が 陽子の内部においても 成り立っているのなら、電子のスピン磁気モーメントも 古典力学に従う必要がある。
しかし このページにあるように、電子のスピン速度は その回転半径が陽子と等しいとき 光速よりも はるかに速くなってしまう ( > c )。
( もちろん、電子は これよりもはるかに小さいため、これよりも さらに速くなる。)
(Fig.34) 陽子外部磁場は キャンセルされる。

すでに述べたように 磁気モーメントの外部の空間全体 (= 球状 ) における 磁場の積分はゼロになる。
なぜなら "上方向" と "下方向" の磁場の大きさは ちょうど同じ だからである。
つまり 全空間における 全磁場は Fig.32 のようになる。
もちろん、電流の形が 円形以外 ( 楕円形とか ) のときは、この値は 変わる。
こういう意味では "モデル依存" の値である。
(Fig.35) 磁場のエリアは 任意に指定できる。
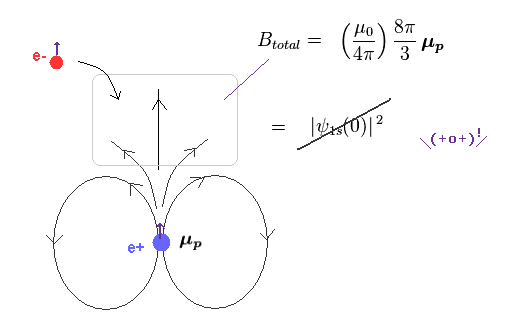
Fig.34 では 陽子外部の 全磁場の積分は キャンセルされると言ったが、もちろん、各エリアの磁場は ゼロではない。
そのため、原点以外のエリアを Fig.32 の全磁場に寄与する部位として選択したとしたら、 電子波動関数の確率密度 (= ψ ) の値が 変わってしまう。 (= ψ(0) でない。 )
結果的に、超微細構造の値は 選択した場所に応じて 変化することになる。
これはつまり、この方法では 超微細構造の値を 指定した場所に応じて 任意に変化することができるため、意味がないのである。
(Fig.36) 計算結果は まだ違う。

超微細構造は "上方向" と "下方向" の原子核スピン間の エネルギー差を表す。
Fig.36 に示したように、 この 古典的なビオ・サヴァールの法則に立脚した方法では まだ 正確な超微細構造の値には ならない。
この古典的な計算手法の後に 別の人為的なトリック を使用する必要がある。
(Fig.37) 電子 (= S ) と 原子核 (= I ) のスピン。

ここでは "S" は 電子のスピン角運動量 (= 1/2 )、 "I" は 原子核スピン (= 1/2 ) である。
磁気モーメントと 角運動量 (= 1/2 ) の比を "量子力学的な" g因子 と呼ぶ。 このサイト参照のこと。
(Fig.38)

そのため S と I の積は 1/2 × 1/2 = 1/4 になる。
このケースでは、 ±1/4 の差は 1/2 になる。
(Fig.39)

ここで、全スピン (= F ) を定義する。
(Fig.40) ↓ 量子力学的な効果 ?

量子力学によれば、F = 1 のときでさえ、F の二乗は "2" になる。
(Fig.41)
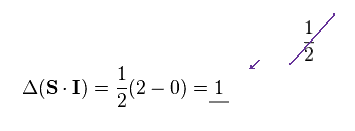
結果、 ±"SI" のおける差は 古典的な場合の 2倍 (= 1 ) になる。
( Fig.41 の "1" と、Fig.38 の "1/2" を比較するといい。これが最後のトリックである。 )
(Fig.42) 人為的なトリック。

結果的に、実験値に近い超微細構造の値を得ることができた。
しかし この方法は はっきり言って かなり強引で かつ
一貫性がない。
Fig.29 に示したように、彼らは まず 純粋な 古典電磁気学の ビオー・サバールの法則を用いて 磁場を計算した。
しかし この最初の定義を すっかり忘れて、量子力学的なトリックの名の元で、この磁場の量を 2倍に倍増してしまったのである。
常識的に考えれば、量子力学に基づく最後の操作が正しいとしたら、最初の 純古典力学的手法は 最初から適用できず、使うことができないことになる。

2014/10/15 updated This site is link free.