
トップページ (2電子原子も含む正確な新ボーア模型)
シュレディンガー方程式は ボーア・ゾンマーフェルト模型の一部である。
シュレディンガー方程式がゾンマーフェルト模型の一部である厳密な証明。
1913 年のボーア理論以降、ゾンマーフェルト、クラマース、パウリ、ハイゼンベルク、ランデ、ラングミュア などの物理学者達が 正確なボーア模型のヘリウムの構造を得ようと研究していた。
通常の物理学の教科書は ボーアの原子は 加速する電荷の影響で エネルギーを放射しながら核に落ちていくと よく説明しているが、この説明は間違いである。
なぜなら 単一電荷の周囲の 真空の電場 (磁場) エネルギーは 古典的な電磁気理論で説明することができないからである。
古典的な電磁気によれば、真空の電場エネルギーは 単一電荷の内部の無限小電荷間の位置エネルギーの総和を意味することになる。
しかし、単一電子は それより小さな電荷からできているわけでもないし 小さく壊すこともできない。( このページも参照のこと。)
つまり、ポインティングベクトルや 真空の電場エネルギーそのものが 単一電子のケースにあてはまらないことになる。
実際に 1920 年代、多くの名だたる物理学者達が より良いボーア模型のヘリウムの構造を得ようと努力していた。
(Fig.1) 観測者の超能力?

相対性理論によれば、 すべての現象は 観測者の動きに関わらず 同じに見えなければならない。
(しかし この非常に厳しい制限が 相対論的な場の量子論や 超ひも理論から リアリティーを排除してしまった。 )
Fig.1 の上のパネルでは、単一の荷電粒子が 等速直線運動している。
そして 観測者は静止しているため この荷電粒子は 電磁波を放射してエネルギーを失わないということになる。
しかし Fig.1 の下のパネルでは 観測者が 加速し始めた。
相対論によれば、観測者の視点からは 荷電粒子が 観測者の代わりに加速していることになる。
つまり、荷電粒子自体の動きは Fig.1 の上下で変わりがないにも関わらず、下のパネルでは 電磁波を放射して運動エネルギーを失っていくことになってしまう。
これは 観測者の超能力を意味しているのだろうか? 非常に奇妙である。
(Fig.2) 古いボーアのヘリウム原子。
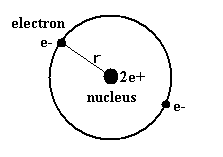
ボーアが最初に思いついた ヘリウム原子では、2つの電子は 同一軌道上の核を挟んだちょうど正反対の位置を運動している。 (Fig.2)
しかし このページによれば、この古いボーアのヘリウム模型の基底状態のエネルギーは -83.33 eV で、これは 実験値 -79.005 eV と 約 5.5 % ほども違う。
また この単純なヘリウム模型は 磁気モーメントを持ち、ボーア磁子の整数倍を常に与える。
もちろん この古いヘリウム模型では ダビッソン・ジャーマーの電子の干渉実験を考慮すれば、2つの電子の互いに反対の位相どうしが打ち消しあって 片方をはじき出してしまう。
( ボーア模型のパウリの排他原理は役に立つ も参照のこと。)
(Fig.3) 2つの電子のドブロイ波が互いに干渉し合っている。
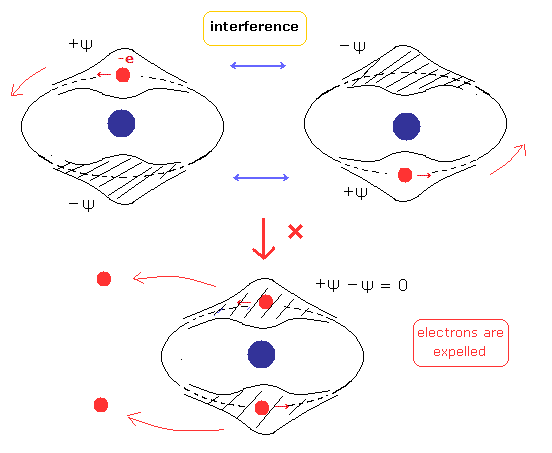
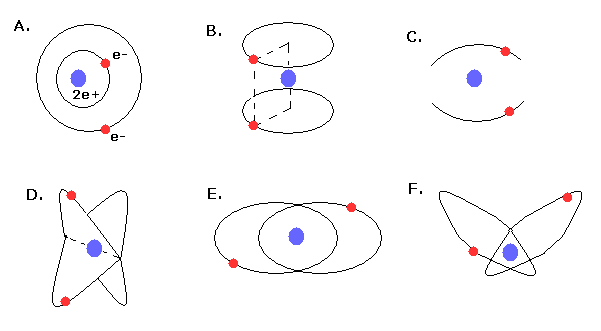
1910 から 1920 年代、ランデ (= 外側と内側の軌道、Fig.4A )、ラングミュア (= 2つの平行な円軌道 - Fig.4B、2つの振動する線状の軌道 - Fig.4C )、クラマース (= 互いに 120°の角度で交わる軌道 - Fig.4D )、ハイゼンベルク (= 同一平面、もしくは 傾いた軌道 - Fig.4E,F ) 達は より良いボーア模型のヘリウムを得ようと努力していた。
しかし コンピューターのなかったこの時代に これらの古いヘリウム模型は どれも正確な基底状態のエネルギーを得ることができず、また ヘリウムの 強固な安定性 や 閉殻性 も説明することができなかった。
(Fig.4) 様々な古いボーアのヘリウム模型。
1980 年代以降も 様々なボーアのヘリウム模型が考案された。( arxiv 0705.4321v2 も参照のこと。)
例えば、2つの電子が 同一軌道上を運動しているが それらの互いの角度は変動できる。
( Fig.5A, J Phys.B, At.Mol.Phys. 16, 2647-2657, 1983, Bohr orbit theory revisited. ).
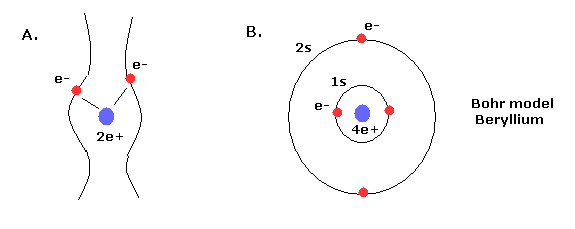
また、Fig.5B は 同一平面上の ボーアのベリリウム原子を表している。 ( http://www.users.csbsju.edu/~frioux/stability/BohrAtoms.pdf )
しかし これらは 計算結果において 量子力学的な変分法にとって代わることができなかった。
準古典的な "WKB" 近似は 量子力学的手法の一つであり、オリジナルのボーア模型とは異なる。
( Theoretical and Mathematical Physics, 151, 659-680, 2007, semiclassical quantization of Bohr orbits in the helium atom ) も参照のこと。
この結果は 基底状態のエネルギーの実験値と 6 % ほど違う。
(Fig.5) ボーアのヘリウム原子模型のいくつかの例
コンピューターを使用すると、電子間の反発力を含む3体問題では 初期条件のちょっとした変化で すぐに電子運動が カオス状態になりやすく 1つの電子が無限遠に飛ばされる オートイオナイゼーション という現象に陥る。
( Phys. Rev. Lett. vol.70, 13, 1928, 1993, Helium atom as a classical Three-Body Problems も参照のこと。)
これはつまり ほぼすべてのケースで高確率で ヘリウムが不安定になり 自然なイオン化が起きてしまうことを意味している。
(Fig.6) 古典的ヘリウム模型における自然なイオン化。

計算の結果、3パターン (トーラス状の) のみ 安定した電子運動状態になることがわかった。
そのうちの1つは 外側と内側に分かれた 2つのリング軌道の模型である (Fig.7)。
2つの電子軌道が互いに離れているときは それらは楕円状になる。
2つの電子が近づくときは トーラス状の軌道は反発力でゆがみ、互いにまた離れていく。
(Fig.7) 古典的ヘリウム原子。

2番目のパターンは 1つの電子が内側で2回 回転する間に もう片方の電子が外側で1回転し その後互いの位置関係を交換するというものである。
3番目のパターンは 内側と外側の電子が 非対称的に振動している模型である。
もちろん これらの模型に 何かクーロン力などの外力を少し加えると 容易に運動がカオスになり 自然イオン化が起きてしまう。
また これらの複雑かつ非対称な模型で 軌道がド・ブロイ波長の整数倍になるという概念を使用することは不可能である。
(Fig.8) 量子力学のヘリウム原子も不安定である。
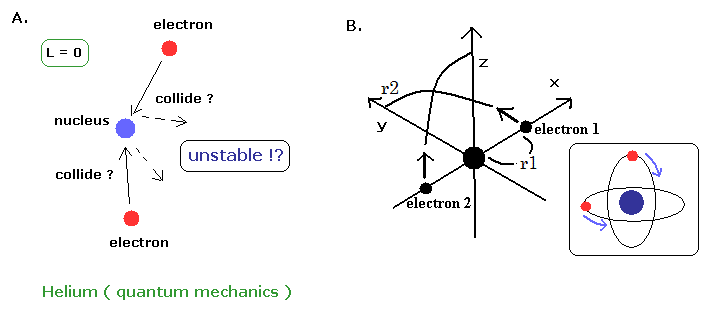
もし Fig.7 の古典的ヘリウム原子が不安定だとすると、Fig.8A の量子力学的なヘリウムも同様に不安定ということになる。
なぜなら 2つの電子の角運動量ともゼロ (L=0) であるため いつも原子核に衝突して はね返ることを繰り返しているからである。
この状態では 2つの電子の波動の位相が カオス的に無秩序になって非常に不安定になると思われる。
一方で 新しいボーア模型のヘリウムでは 2つの電子の波の位相は安定 しており、かつ互いに打ち消しあったりはしない (ダビッソン・ジャーマーの電子干渉実験とも矛盾しない)。
また この新しい模型では 水素原子のように 軌道が ちょうど1 ド・ブロイ波長 になる。
( 基底状態の計算結果も -79.005 eV で この値は 量子力学の最新の計算結果よりも正確である。)
このページに示したように、2つの電子が 安定かつ 決まった軌道を持つことは非常に重要なことである。
もし 2つの電子軌道が クーロン力などのわずかな外力で 容易に変化することがあるならば、それらの電子波の位相は すぐにカオス的状態になって 互いに打ち消しあってしまう。
( なぜなら 2つの電子は ほぼ原子核を挟んだ逆の位置に存在しているからである。)
しかし ご存じのとおり、ヘリウム原子は すべての原子の中でも とりわけ安定して かつ不活性である。
よって Fig.8B のヘリウムは 妥当な模型といえる。
(Fig.9) 新しいボーアのヘリウム原子 (= A.) は 分極しない。.
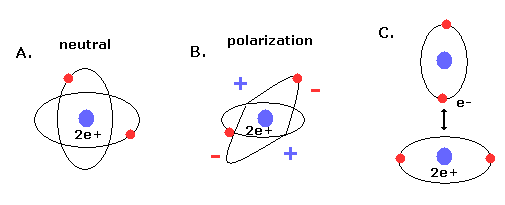
さらに 2つの電子軌道が ちょうど対称的でかつ 互いに垂直に交わっていると、原子核の周囲で 電子のマイナス電荷が 均等に分布し 電荷の分極が起こらない (= Fig.9A, neutral )。
もし 2つの電子軌道が不均等だと 原子核周囲で マイナス電荷の不均等分布が起きて分極がおこる (= Fig.9B )。
電気分極した原子などは 他の原子と相互作用して弱い結合を形成しやすい ( 例えば Fig.9C )。
つまり これらの場合では ヘリウムが容易に 液体の状態に凝集しやすくなり これは事実とは異なる。
1920 年代、ボーアやゾンマーフェルトは ”量子化された角運動量”が最も重要な概念だと考えていた。
なぜなら 1923 年の ド・ブロイの学術論文以前に ド・ブロイ波長の整数倍という概念がなかったからである。
しかし この量子化された角運動量という概念は ある意味 厳しすぎると言える。
例えば、Fig.8B の新しいボーアのヘリウム模型は 2つの電子が同一平面上にないので 必ずしもある視点からみれば 総合的な角運動量は量子化されていない。
この非常に厳しい条件のために、彼らはついに 半整数倍の奇妙な電子スピンという概念を導入することになった。
しかし このページに示したように 量子力学によれば 軌道もしくはスピン角運動量は 正確には 整数 もしくは 半整数ではない。
(Fig.10) 本当の角運動量は 複雑?

量子力学によれば、本当の角運動量は l(l+1) の平方根 ( スピンの場合は s(s+1) の平方根 ) である。
彼らは 歳差運動のせいで 整数もしくは 半整数に”見える”と主張している。
ちょっとできすぎた話だと思わないだろうか?
(Fig.11) ボーアの水素分子イオン (H2+) ?
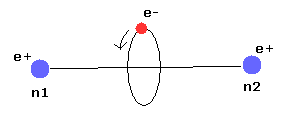
1920 年代、ボーアは 水素分子イオンでは その 1つの電子軌道面が 2つの原子核のちょうど中間にあり かつ2つの核をつなぐ線と垂直に交わっていると考えていた。
また パウリは博士論文のテーマに このボーアの水素分子イオンを取り上げようとしていた。
しかし Fig.11 の模型は 非常に不安定な構造で これは実験結果と異なる。
(Fig.12) 水素分子イオン (H2+)
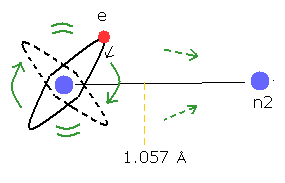
Fig.11 の不安定で非現実的な模型の代わりに、Fig.12 の水素分子イオンは 安定である。( このページも参照のこと。 )
もちろん より正確な値を得ようとするなら コンピューターに頼るしかなく 1920 年代では不可能である。
H2+ の非常に長い原子核間距離を考慮すれば、電子はおもに 2つの原子核のどちらか一方に属していると考えるのが極めて自然である。
( "中間地点" は非現実的である。 )
量子力学は正確な水素分子イオン模型を計算できたとされている。
しかし ご存じのとおり、量子力学の水素分子イオンは はっきりとした具体的な構造を示してくれないので、他の分子などにこのモデルを応用することができない。
( 現在の量子化学は ナノテクノロジーで役に立たない。も参照のこと。)
また ヘリウムを含めた他の原子と同じく、量子力学の波動関数の確率分布は 常に無限遠まで広がっており 非現実的である。
現在の量子化学では、密度汎関数法 (DFT) が支配的な手法になっている。
しかし DFT は 波動関数全体を1つのものに統合してしまったために パウリの排他原理 (= いわゆる交換エネルギー ) を正確に扱えなくなってしまった。
結果的に DFT は 完全に人為的な近似に依存せざるを得ない。
また このページに示したように 私たちの世界の非常に重要な臨界次元を決定するさいに 果たして 単なる数学上の定義である "ゴースト" や "グラスマン数" に全面的に頼ってよいものだろうか?

2012/8/29 updated This site is link free.