トップページ (正確な新ボーア模型)
特殊相対論は間違っている。
直角レバー と 電線の回転。
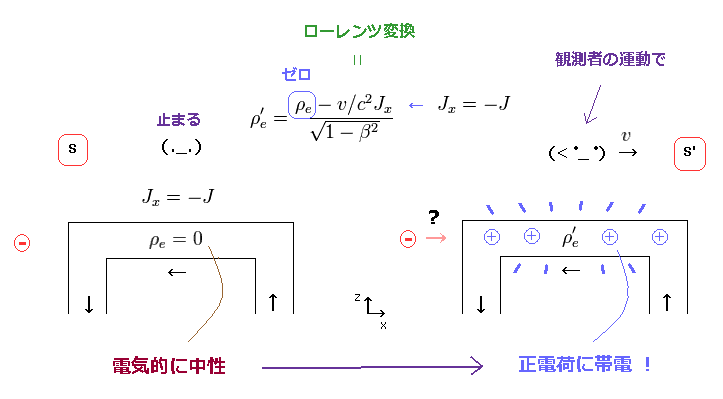
(Fig.1) ローレンツ変換 → 新たな電荷 (= ρ'e ) が 発生する ↓

相対論によれば、 電荷 (= ρe ) と 電流 (= J ) は 固定した概念ではない。
これらは ローレンツ変換の下では、時空間変数 (= ct, x, y, z ) と同じように変換する。
ここ (p.16)、
ここ (p.3)、 ここ (p.9) などのサイトを 参照のこと。
相対論の基礎に関しては まず このページを参照のこと。
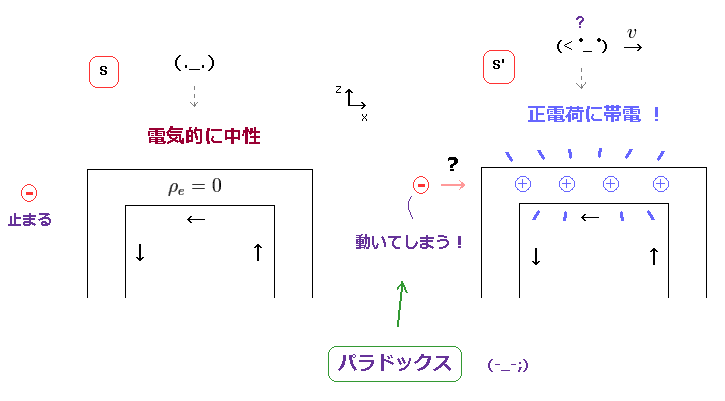
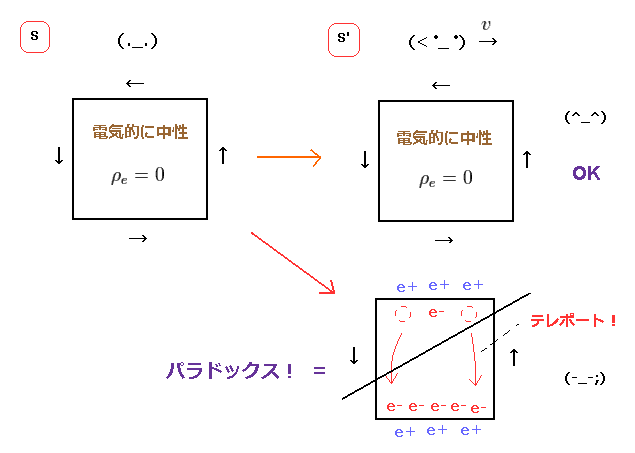
Fig.1 左 (= S' ) では、中性の電線に電流が流れている。
しかし 観測者が 動きだした瞬間に、新たな "正電荷" が 電線内に 生じてしまうことになる (= Fig.1 右、 S' )。
(Fig.2) 電荷 (= ρ ) と 電流密度 (= J ) のローレンツ変換。
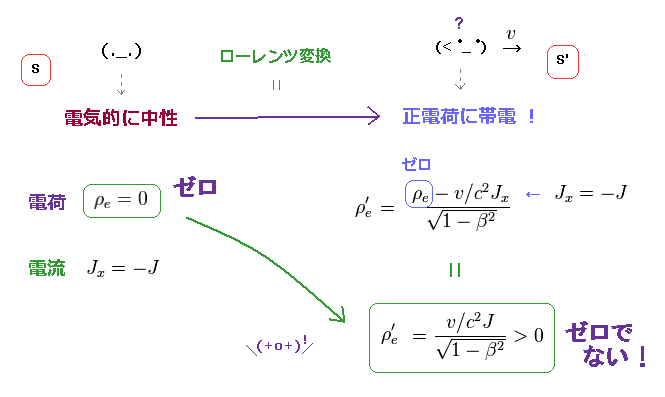
ローレンツ変換によって、電荷密度 (= ρe ) と 電流密度 (= Jx ) は 混ざることになる ( Fig.2 右上図 )。
結果的に、元の電荷が ゼロだとしても ( ρe = 0 )、 中性の電流 (= Jx ) が S' 慣性系のみに 新たな電荷 (= ρ'e ) を発生させてしまうことになる。
(Fig.3) 電荷 (= ρ ) と 電流 (= J ) のローレンツ変換。
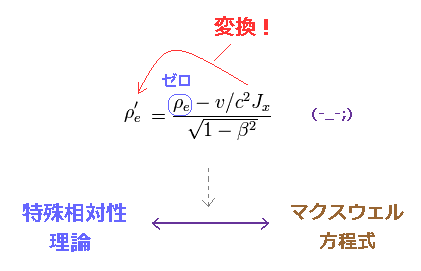
この非現実的な変換は 特殊相対論が マクスウェル方程式と 融合するのに 必要不可欠なものである。
要するに、上記の変換式が成り立つと マクスウェル方程式が ローレンツ変換によっても その形を保てることになる。
光速 "c" は マクスウェル方程式によって 導出される。
つまり マクスウェル方程式が あらゆる慣性系で成り立つことが
一定の光速 "c" を説明するのに必須になってくる。
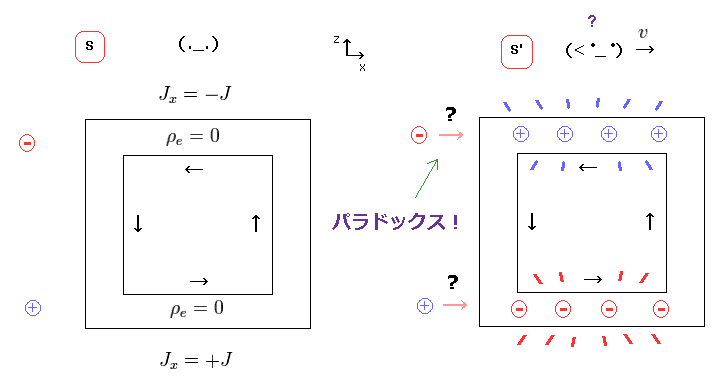
(Fig.4) 負電荷が S' 系でのみ 電流方向に引かれる?
もし 上記の電荷と電流の変換が正しいとしたら、致命的なパラドックスが出現してしまう。
Fig.4 では、電線の外で 負電荷の粒子が 静止している (= S 慣性系 )。
しかし、観測者が動きだした瞬間に、奇妙な正電荷が 電線内に生じてしまうことになる。
結果的に 負電荷が S' 系でのみ 電線方向へ 引き付けられることになる。
これは明らかにパラドックスであり、もちろん解決されていない。
残念ながら、この種の 本当のパラドックスは 一般の方々から 完全に 隠されてしまっている。
(Fig.5) ローレンツ力には 新たな電荷の発生が必要。
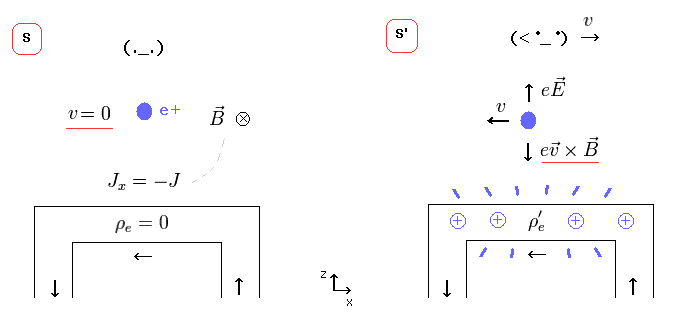
それでは、どうして 奇妙な正電荷が 中性の電線から 発生するのだろうか?
Fig.5 左 (= S ) では、静止した観測者が 電流 J が流れている中性の電線を見ている。
つまり、S 慣性系では、電場 E は ゼロであり、磁場 B が y 方向に発生している。
正電荷粒子 (= e+ ) は S 系では静止しているため、それは 磁気力を受けていない。
しかし 観測者が x 方向へ動きだすと、その視点 (= S' ) からは 正電荷粒子が反対方向へ 動いている。
これはつまり、この電荷は速度を持つことになり ローレンツ力を受けて S' 系でのみ 電線方向へ 曲がってしまうことになる。
もちろん、これは 明らかにパラドックスである。
この問題を解決するために、新たな電荷が 発生して この磁気力を
キャンセルする必要がでてくるわけである。
このサイト
や このサイト 参照のこと。
(Fig.6) 磁気力は 粒子の速度 (= v ) に依存する。
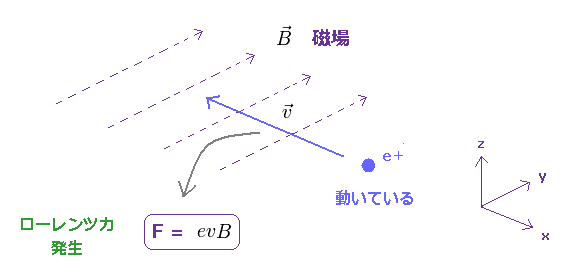
ある荷電粒子が 速度 "v" で 磁場 B の中を運動しているとき、それは ローレンツ磁気力 ( F = evB ) を受ける。
この磁気力は その速度と磁場の両方向に 垂直な向きに発生する。
このサイトに向きの関係が載っている。
(Fig.7) 粒子が静止しているとき、ローレンツ力は ゼロになる。
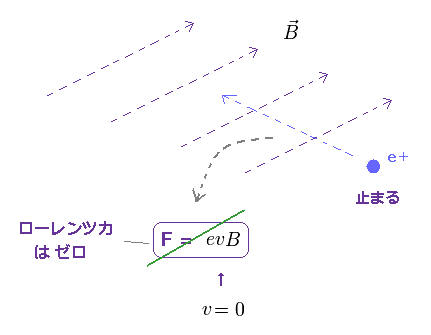
ローレンツ磁気力は F = ev×B. ( "×" は 外積. ) の関係式で与えられる。
つまり、荷電粒子の速度が ゼロ ( v = 0 ) のとき、それは 磁気力を 何も 受けないことになる。
(Fig.8) 観測者と 電荷が S 系で静止している。
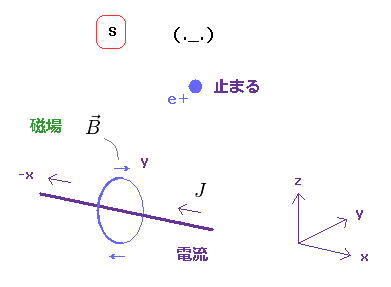
Fig.8 の S 系では、観測者と 電荷 (= e+ ) が静止している。
また 電流 J が流れている 中性の電線がある。
電荷の速度は ゼロのため、それは 磁気ローレンツ力を 何も 受けず、 静止したままとなる。
(Fig.9) 動く観測者 (= S' ) からは、電荷が動き、磁気力が発生?
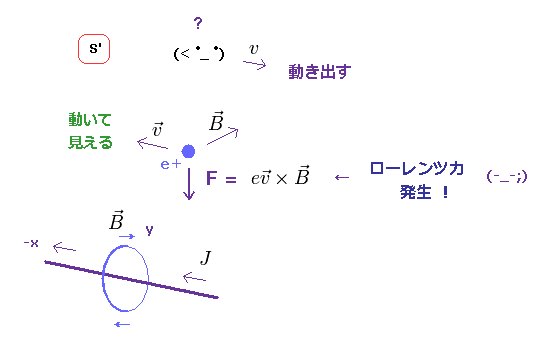
もし この観測者が 動きだすと (= S' )、その視点からは 荷電粒子が 逆方向へ動いて見えることになる。
結果的に、S' 系では、この電荷は 電流から ローレンツ力を受けて 電線方向へ
引き付けられてしまうことになる。
これは 明らかに パラドックスである。
なぜなら Fig.10 に示したように この電荷は S 系では 静止しているが、S' 系では 電線方向へ 動いてしまうからである。
(Fig.10) 観測者が動くと (= S' )、電荷が 電線に近づく !?
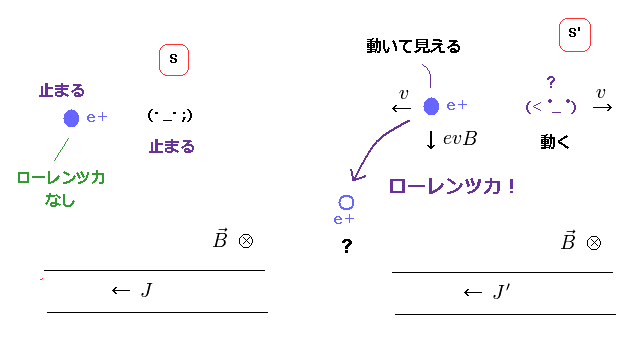
ローレンツ力は 荷電粒子の速度に応じて変化する。
この速度は 観測者が 静止しているか 動いているかで 違って見える。
そのため、ローレンツ力と 特殊相対論が正しいとしたら、観測者は 触れずして 粒子を動かせる 超能力を 持っていることになってしまう。
( S' 系でのみ 荷電粒子が 電線方向へ動く。)
(Fig.11) 観測者の運動のみで 中性の電線が 正電荷に変わる?
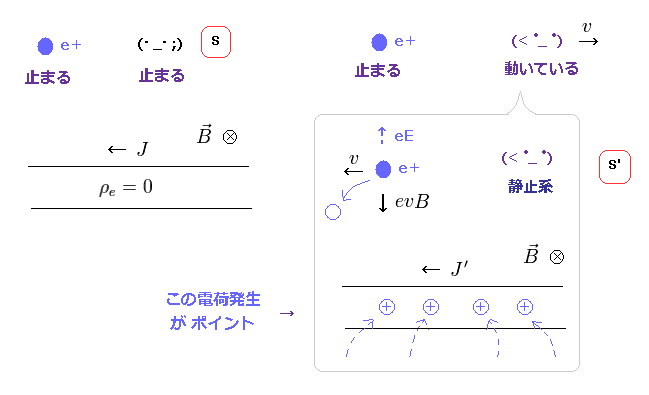
Fig.10 のパラドックスの状況を回避するには Fig.11 右に示したように、この 中性の電線が S' 系でのみ 新たな 正電荷 を発生させなければならない。
(Fig.12)
もし 電線が 正に帯電しているとしたら、新たに発生した電場 (= E ) が 磁気力を キャンセルできることになる ( eE = evB、Fig.12 右 )。
つまり、Fig.10 のパラドックスが解決されるとしている。 ここ や ここ (p.4) なども参照のこと。
しかし この変換は 別の 致命的なパラドックスを生じさせてしまう (= Fig.13 )。
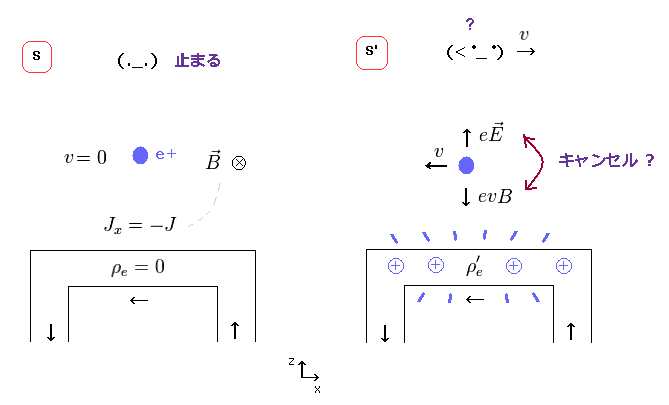
(Fig.13) 特殊相対論の弱点。
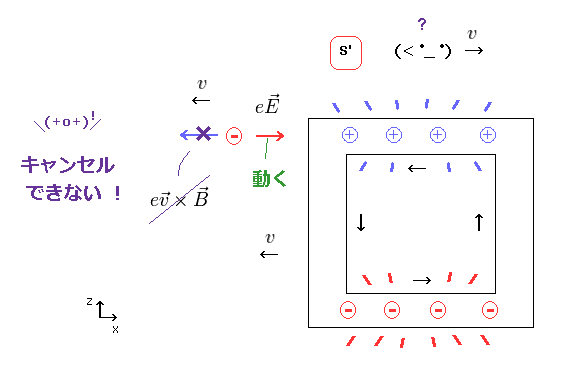
荷電粒子 (= 負電荷 ) が Fig.13 の位置にあるとき、この粒子は S' 系でのみ 電線方向へ 引き付けられてしまう。
なぜなら この粒子に作用する電気力は 磁気力によって キャンセルできないからである。
観測者の動きに応じて、この荷電粒子が 電線方向へ 動くかどうかが決まってしまうわけである。
これは明らかに パラドックスであり、特殊相対論が 間違いであることの証拠である。
(Fig.14) 磁気力 (= evB ) が 電気力 (= eE ) をキャンセルできない。
観測者が x 方向へ動いているとき、電線と粒子は マイナス x 方向へ動いている。
磁気力は 粒子の速度に 垂直な方向に発生する。
つまり この磁気力 (= evB ) は x 方向にはなれないことになり、x 方向の電気力 (= eE ) をキャンセルできないことになる。
結果的に、この荷電粒子は S 系では静止しているが、S' 系では 電線方向へ
加速されることになり、 "パラドックス" ということになる。
ビオ・サバールの法則によれば、この電流は x 方向に磁場を生じることができない。
つまり この荷電粒子の地点には 磁場の影響がないことになる。
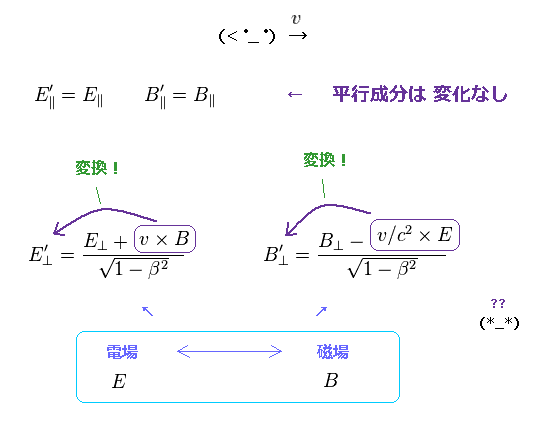
(Fig.15) 電場のローレンツ変換。
上のセクションでは、電荷と電流の視点から どうして致命的なパラドックスが生じるのか説明した。
もし 電荷と電流の変換が 矛盾しているとすると、当然 電磁場の変換も おかしくなっていることになる。
ここ (p.4)、ここ (p.8)、ここ、 ここ (p.91) のサイトにあるように、E, B 電磁場のローレンツ変換は Fig.15 のようになる。
観測者の運動方向に 平行な E, B 電磁場は 変化 しない。
それに垂直な E, B 電磁場のみが 変換して 混合することになる。
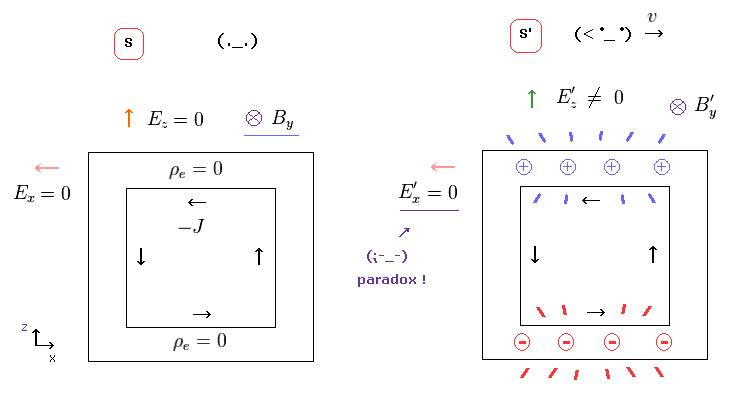
(Fig.16) 電場 E'x はゼロ、 しかし E'z は ゼロでない。 ← Paradox !
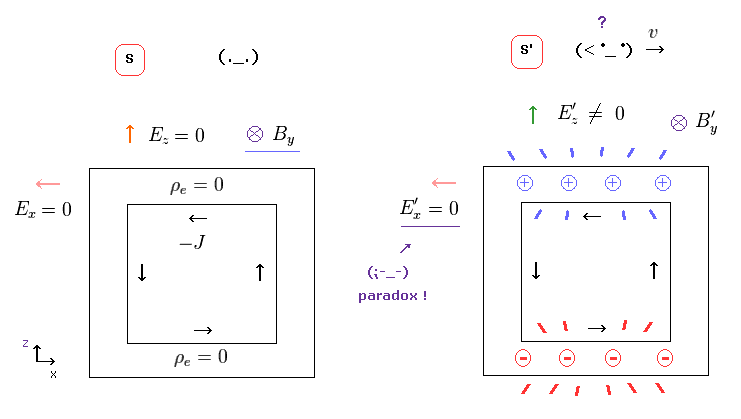
もし Fig.15 のローレンツ変換が正しいとすると、非常におかしな状況が発生してしまう。
Fig.16 左 (= S ) では、すべての方向の電場は ゼロであり、 磁場 B のみが存在する。
Fig.16 右 (= S' ) では、 平行成分である E'x の電場のみ ゼロのままである。
しかし、 E'z は ローレンツ変換で ゼロでなくなってしまう。
(Fig.17) ↓ こういう電荷は 実在するの ?
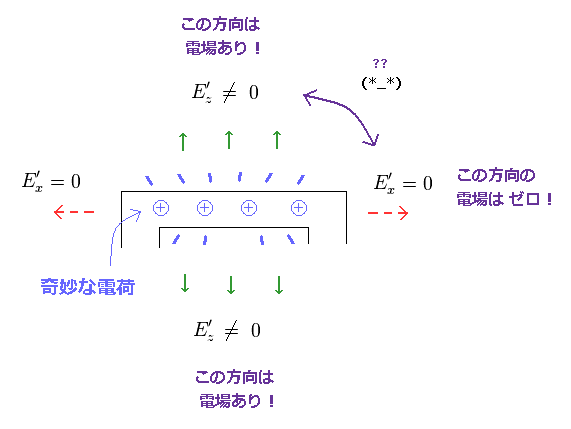
お気づきのとおり、この状況は パラドックス以外何者でもない。
電線内の正電荷は E'z ( と E'y ) の方向の電場のみ 発生させることができ、 E'x は 発生できないことになる。
この現実の世界では このような 非現実的な電荷が 存在するはずがない。
(Fig.18) 相対論では S' 系でのみ 負電荷が取り除かれる?
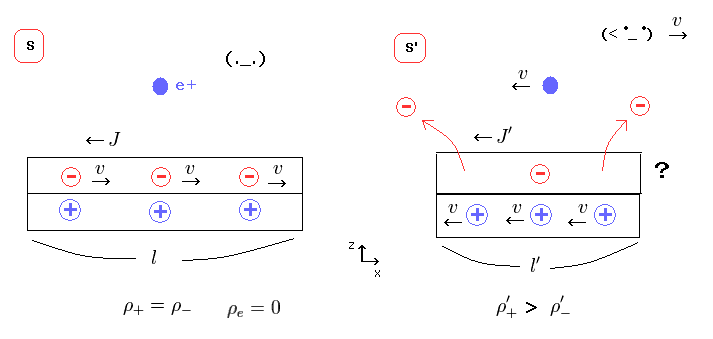
中性の電線が 正に帯電するということは、負の電荷が 電線から
取り除かれるということを意味する。
観測者が 触れずして、これらの負電荷を取り除くことは はっきり言って あり得ない事実であるが、相対論は それを強制しているのである。
(Fig.19) 相対論では、観測者が 負電荷を "テレポート" できる?
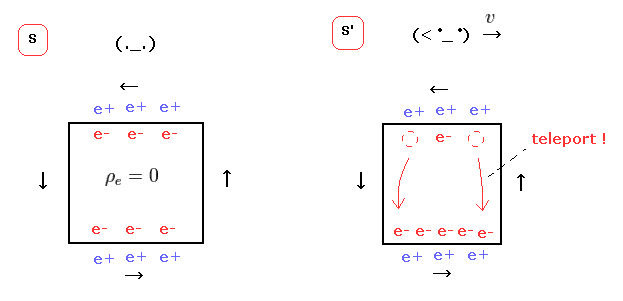
上下の電線には 互いに逆方向の電流が流れている。
つまり、S' 系では、上部の電線が 正に帯電し、下部の電線が 負 に帯電することになる。
結果、この回路の全電荷量は保存されると 物理学者達は主張しているわけである。
しかし もし この考えが本当だとすると、観測者が 自身の動きのみによって 電荷をテレポートできる "超能力" を持てることになってしまう 奇妙としかいいようがない。
(Fig.20) 電子が下部の電線にテレポートする → 反発力 ?
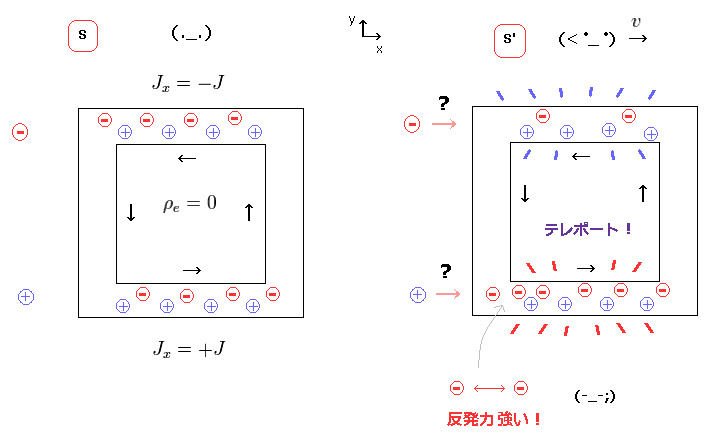
相対論の 4元電流密度の定義によれば、上部の電線内の 負電荷が 観測者の単純移動のみで 下部の電線にテレポートしてしまうことになる。
この場合、Fig.13 に示したように 致命的なパラドックスが生じてしまう。
お気づきのとおり、Fig.20 の状態は 非常に不自然である。
なぜなら、下部電線内に負電荷優位になれば、クーロン反発力が強くなってしまうため、そもそも このテレポート自体が 起きるはずがないからである。
もちろん、クーロン力は すべての慣性系で 働かなければならないことは言うまでもない。
結果的に、相対論は 自然界の 基礎的な法則に 反していることになる。
(Fig.21) リアルな世界では、観測者は テレポートさせる特殊能力を 持ってはいない。
あなた方も感じられたように、電気的に中性な電線は 観測者の運動に
関係なく 中性のままなのは 当たり前の話である。
そうなるには、Fig.8,9 のような 観測者の速度によって ローレンツ力が変化するという考えを
改める必要がでてくる。
(Fig.22) "地球" に対して、観測者が 動く もしくは 静止?
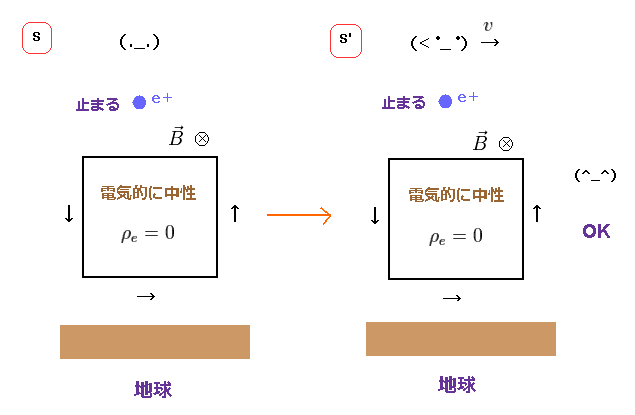
もし 観測者が 対象のローレンツ力と 何の関係もないとしたら、磁気力が生じる生じないかを決める 別のファクターが存在しなければならない。
私達の周囲を見渡せば、空気も含めたすべての物質が 地球と共に動いている。
あなたが 速い速度で走り出せば、向かい風を感じることができる。
このように、荷電粒子が 地球 (エーテル) に対して動いているとき、 それは ドブロイ波を生じさせ、周囲に磁場を作り出すと考えると すべてがしっくりくる。
この場合は、ローレンツ力の致命的なパラドックスは 起きず、観測者も "不自然"な力を 持つ必要がなくなる。
(Fig.23) 1つの電線が 2つに "分離" してしまう?
標準的な相対論では、これらの奇妙な現象を 電荷間の距離で説明しようとしている。 ここ、 ここ、 ここ など参照のこと。
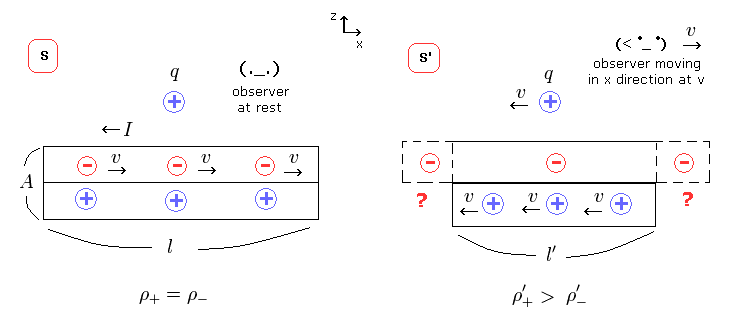
Fig.24 左では、この中性の電線には 同じ数の 負電荷と正電荷が含まれている。
S 系では、負電荷のみが 速度 "v" で x 方向へ 動いている。
観測者が x 方向へ 速度 "v" で動きだしたとき (= S' 系 ) 、その視点からは 負電荷は 静止しており、代わりに 正電荷が -x 方向へ動きだすことになる。
(Fig.24) 電荷間が ローレンツ収縮 もしくは 静止長?
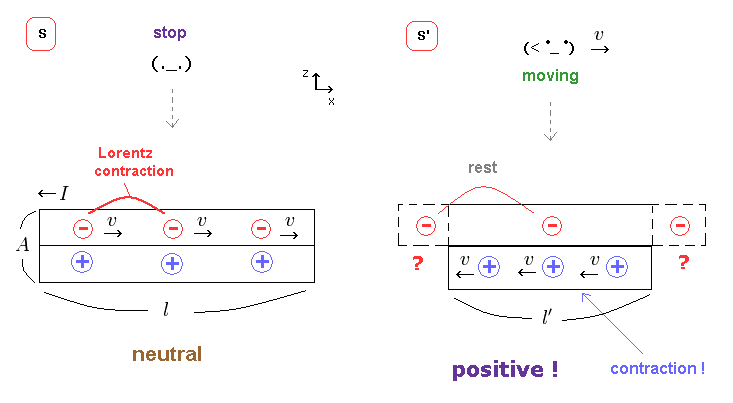
ローレンツ収縮によれば、 Fig.24 左では、負電荷は動いているため、その電荷間距離は 収縮していることになる。
この電線は 中性であるため、負電荷と正電荷間の距離は 同じである。
S' 系では、負電荷間の距離は 元の静止長に戻ることになる。
一方で、正電荷間の距離は ローレンツ収縮する。
(Fig.25) 電荷間距離が短くなる → 密度が増加。
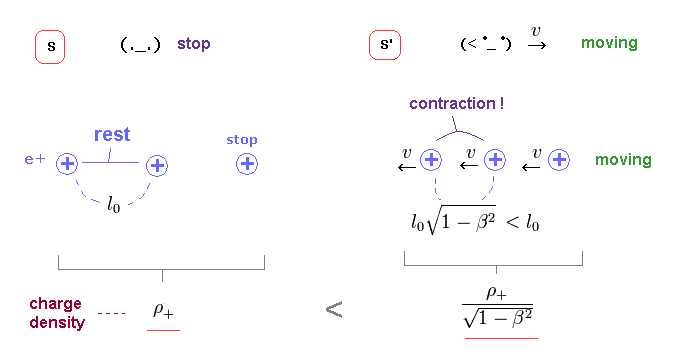
S 系では、正電荷間の静止長は l0 であり、電荷密度は ρ+ である。
一方、 S' 系では、それらの間の距離は ローレンツ収縮しており、Fig.25 右のように 電荷密度が増加することになる。
(Fig.26) 電荷間が長くなる → 負電荷密度は減少する。
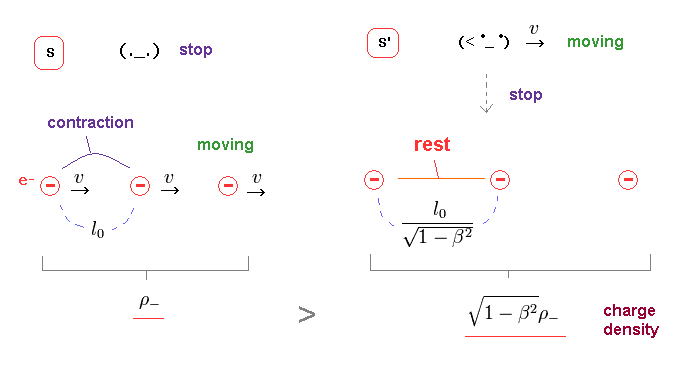
一方で、負電荷間の距離は S 系の状態で 元から ローレンツ収縮している。
S' 系で 観測者が これら負電荷と同じ速度で動きだしたとすると、その距離は 元の静止長に戻り、すなわち 伸びることになる。
なぜなら、S' 系の観測者からは 負電荷が静止して見えるからである。
結果的に S' 系では 負電荷の密度が 減少することになる。
(Fig.27) 電線は S' 系では 収縮する。
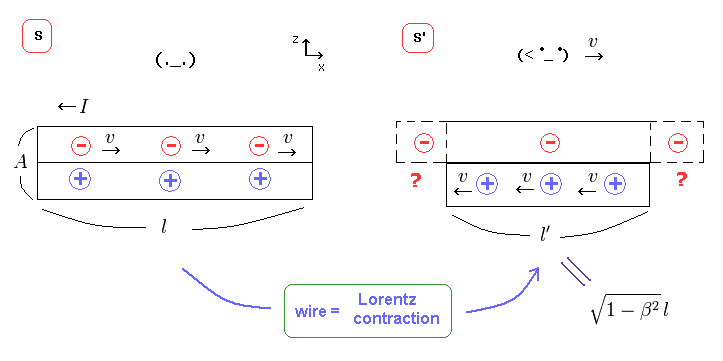
電線自体は S 系で 静止している。
つまり S' 系では 動いているため 電線の長さは ローレンツ収縮 ( l → l' ) することになる。
(Fig.28) 全電荷量 = 電荷密度 × 電線の長さ。
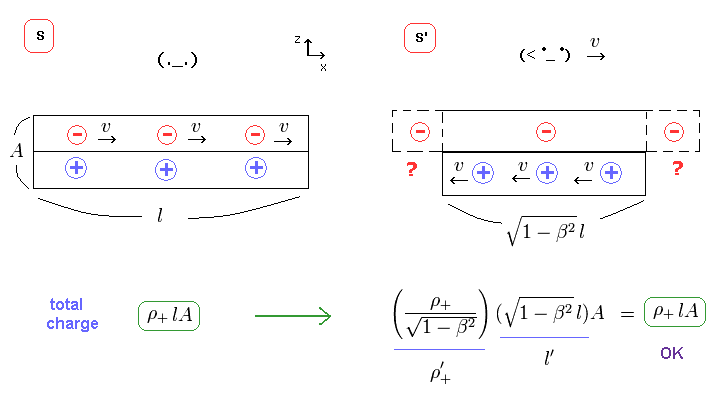
全電荷量は 電荷密度 (= ρ ) × 電線の体積で与えられる。
Fig.25 と Fig.27 から、 全正電荷量は S と S' 系で 同じになる。
(Fig.29) 全負電荷量は 減少する。
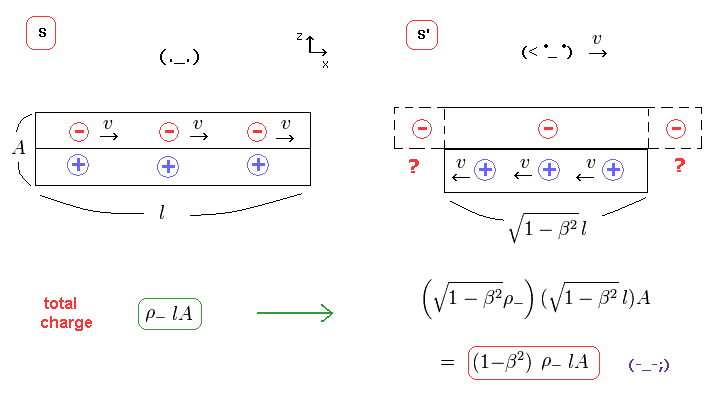
Fig.26 と Fig.27 から、負電荷量のみが 保存しないことが分かる。
なぜなら 負電荷密度の減少分を 電線の長さで キャンセルできないからである。
(Fig.30) S 系での 中性の電線。
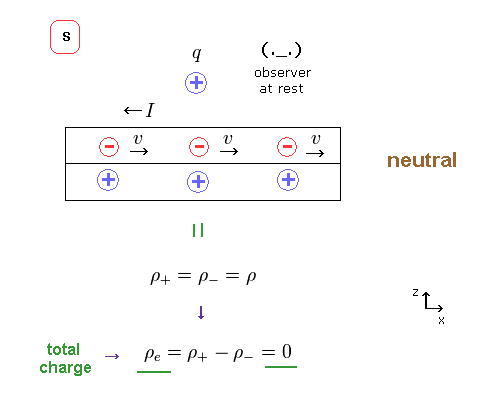
S 系では、正電荷と負電荷量は同じである。
( ρ+ = ρ- = ρ )
(Fig.31) S' 系では 全電荷は 正になる。
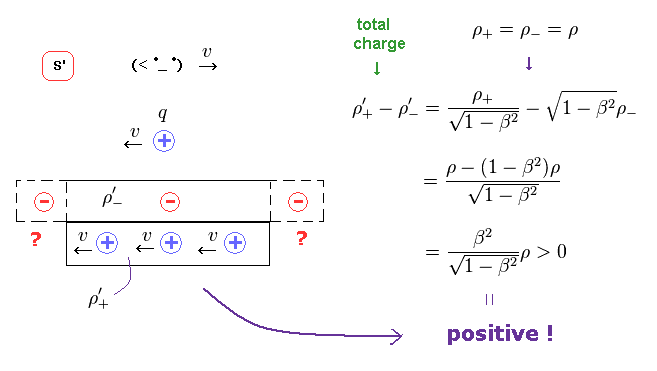
正電荷 (= Fig.25 ) と 負電荷 (= Fig.26 ) を足して、この電線の全体の電荷 ( 密度 ) は Fig.31 に示したように S' 系で 正になる。
(Fig..32) 電荷と電流のローレンツ変換。
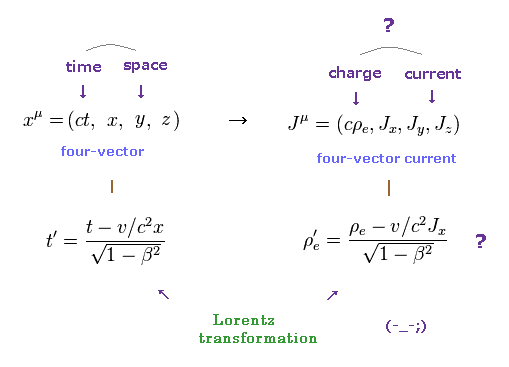
特殊相対論によれば、 電荷密度 (= ρ ) と 電流密度 (= J ) は ローレンツ変換の下で 時空間座標 (= t, x, y, z ) と同じように変換する。Eq.1 参照。
そのため これらを 4元電流密度 と呼ぶ。
(Eq.1) 電荷 (= ρ ) と 電流 (= J ) のローレンツ変換。
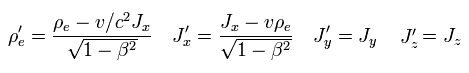
(Fig.33) S' 系における 電流 J'x。
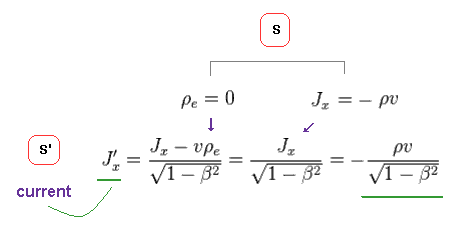
S 系では、全電荷量は ρe = 0 ( 中性 ) で、電流は Jx = -ρv である。
Eq.1 を用いると、電流密度 J'x は Fig.33 で与えられる。
(Fig.34) S' 系における 電場 (= E' ) と 磁場 (= B' )。
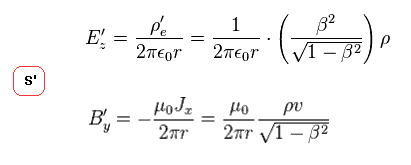
線電荷が作る電場 (= E ) は このサイトに載っている。
磁場 (= B ) は このサイトに 載っている。
Fig.31 と Fig.33 の結果を これらの式に代入すると、電線周囲の 電磁場は Fig.34 のようになる。
(Fig.35) S' 系においても、運動の z 方向は ゼロである。
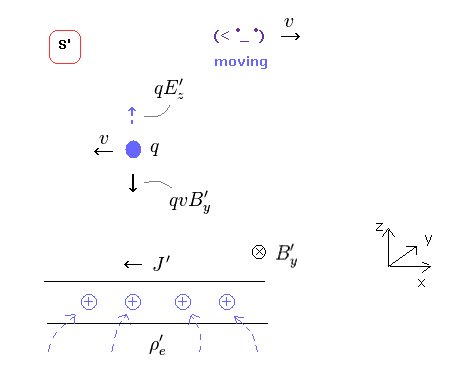
S 系で 粒子の速度の z 成分が ゼロのとき、S' 系でも 当然 ゼロのままでなければならない。
つまり、z 方向では 新たに発生した電気力は 磁気力によって キャンセルされなければならない。
( qE - qvB = 0 )
Fig.34 を用いて、荷電粒子に作用する z 方向の力は Fig.36 に示すように キャンセルされて ゼロになることが分かる。
(Fig.36) S'系においても z 方向の 力の総量は ゼロになる。
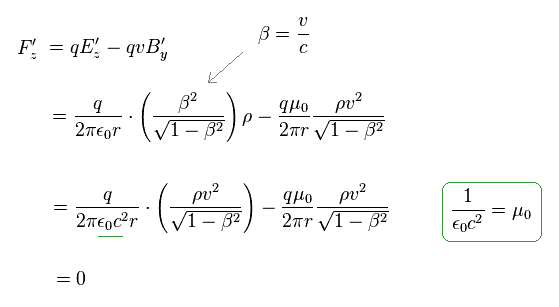
結果的に、 S と S' 系の両方で、粒子に作用する z 方向の力の総量は ゼロになる。
そのため パラドックスは キャンセルされると 彼らは主張しているわけである。
Fig.13 と Fig.14 に示したように、新たに生じた x 方向の電場は ローレンツ磁気力で キャンセルすることができない。
この方向が 相対論の弱点であり、すなわち 相対論が間違いであることの証拠である。
(Fig.37) 電子の電荷 (e-) は ローレンツ変換で不変な定数。
量子電磁力学 (QED) によれば、素電荷 (e-) は ローレンツ変換で不変な定数である (= スカラー量 )
実際、電荷 e は 微細構造定数や磁気能率に定数として使われている。
( 正確には 電荷 e と 真空の誘電率の組み合わせが不変。)
ここでは この不変性を 古典電磁気学と特殊相対論の視点から説明してみることにする。
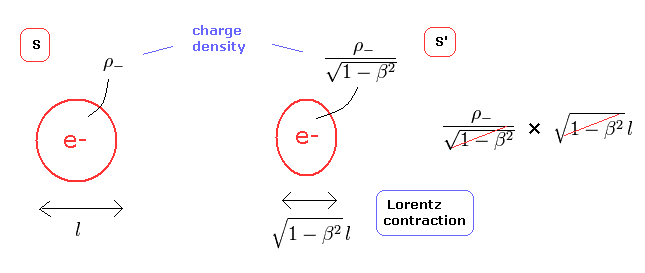
電子は 点電荷だが、その長さが "l" であると仮定する (Fig.37 左)。
Eq.7 と ローレンツ収縮より、1つの電子の全電荷 e- は ローレンツ変換で変化しない (= Fig.37 右)。
なぜなら たとえ 長さ "l" が収縮したとしても、電荷密度 ρ は増加して (= Eq.1)、キャンセルしあって、トータルの電荷量は変化しないからである。
(Fig.38) 全電荷は すべての慣性系で保存する。
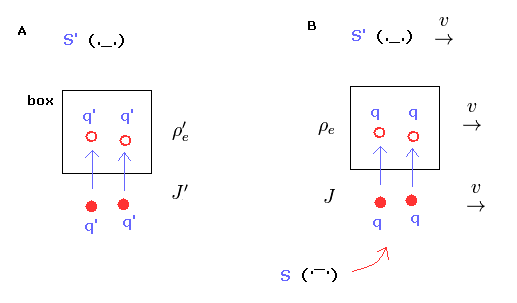
Fig.38 では、電荷と箱が S' 慣性系とともに 速度 v で S 系に対して 動いている。
S' 系で、2つの電荷 (= 2 × q' ) が 時間 dt' の間に 箱に中に入ったとする。つまり 時間 dt' の間に 箱の中の電荷量が 2q' 増えたことになる (= Fig.38A )。
S 系からの視点では 電荷 q' が q になるとする ( 実際には 単位電荷 "e" は 変化しない )。
S 系においても、2つの電荷 (= 2 × q ) が 時間 dt の間に 箱の中に入り、すなわち 時間 dt の間に 2q の電荷量が 箱に中に増えたことになる。
つまり、あらゆる慣性系において 電荷密度 ρe と 電流密度 J の関係式が 成り立たなければならない。
( つまり 毎秒 Q の電荷が ある場所に入っていけば、毎秒 Q の電荷がそこに増えるという当たり前の話である。)
(Fig.39) 電荷密度と電流密度の関係。
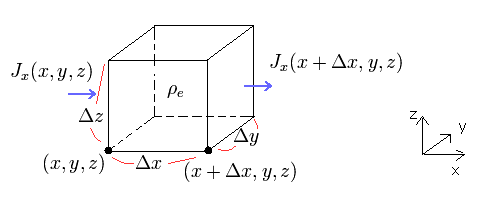
Fig.39 では、 電荷密度 ρe は 単位体積あたりに含まれる電荷を意味している。また 電流密度 J は、単位断面積を通過する電流を意味している。
つまり、電荷の動きを考慮すると、無限小の箱 ( V = Δx Δy Δz ) における 電荷、電流密度の関係式は
(Eq.2)
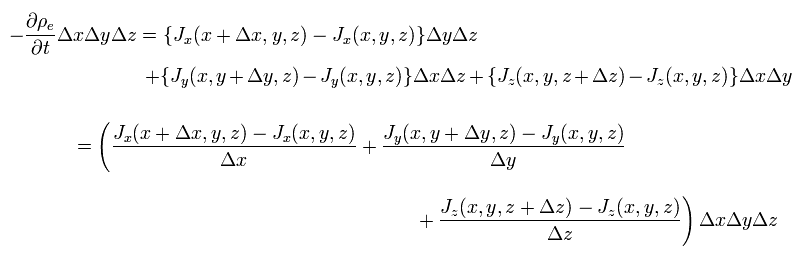
電流 (= J ) の x, y, z 全方向の変化の総量は 箱内部の 電荷密度 (= ρ ) の変化を引き起こす。
電荷密度 ρe = C / m3 (= 単位体積あたりのクーロン量 )、 電流 I = C / s (= 毎秒通過するクーロン量 )、電流密度 J = C / s m2 (= 単位面積を毎秒通過するクーロン量 ) である。
Eq.2 から 次を得る。
(Eq.3)
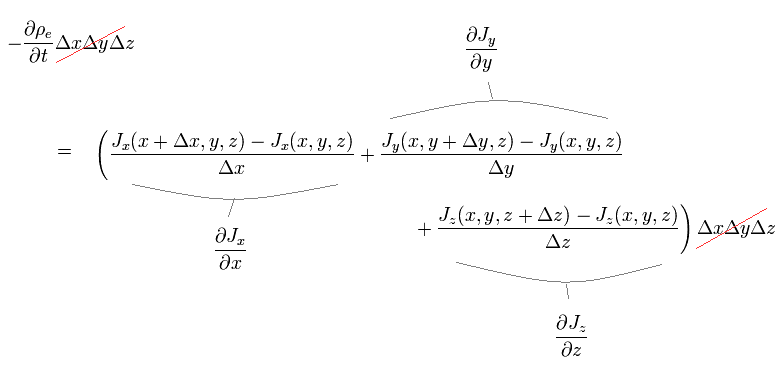
結果的に、
(Eq.4)
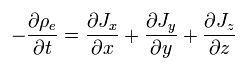
Eq.4 の電荷密度と電流密度間の関係式は すべての慣性系で それぞれ 全電荷量が保存するため、満たされなければならない。
もし あなたがたが特殊相対論を信用しているとしたら、時間 (= ct ) と 空間 (= x, y, z ) の座標は ローレンツ変換で 4元ベクトルとして変化しなければならない。
( もちろん 特殊相対論のかわりに "地球のエーテル" を認めたら この奇妙なローレンツ変換を 使用する必要がなくなる。 )
(Eq.5)
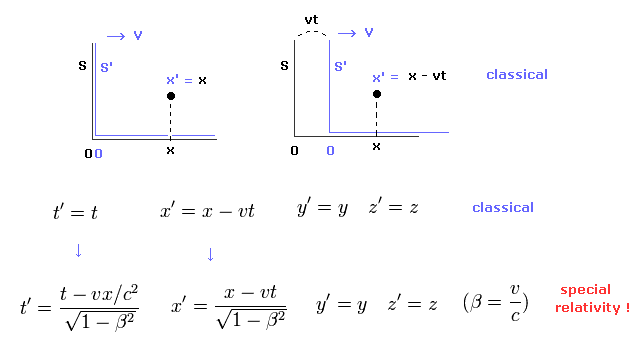
ここでは S' 慣性系 (= x', y', z', t' ) が S 系 (= x, y, z, t ) に対して 速度 v で x 方向へ運動している。
Eq.5 は 次に等しい。
(Eq.6)
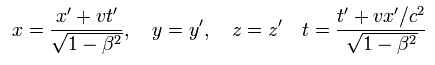
すべての慣性系において、Fig.38 の 電流、電荷密度の関係式が満たされる必要がある。
(Eq.7)
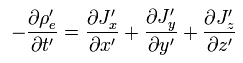
Eq.7 を満足するためには、電荷密度と電流密度が 時間と空間の座標のように 4元ベクトルとして変化しなければならない。これが 奇妙な現象を引き起こす。
そして このことによって 電磁気学における特殊相対論が破綻することになる。
(Fig.40)
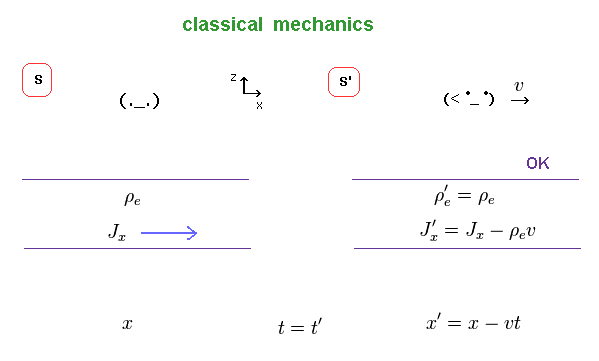
最初に Eq.5 上の 古典力学バージョンについて考える。
古典力学では、時間、空間、電荷などの奇妙な変換は もちろん 起きない。
ごく 自然な変換だけを考えればいい。
S' 系が x 方向に 速度 v で動いているため、 S' 系では 電流 Jx に - ρe v (= 電荷密度 × 速度 ) を つける必要がある。
(Eq.8) 古典力学。
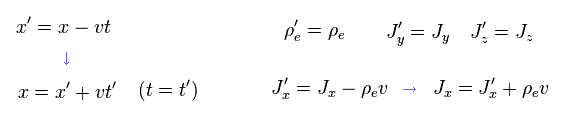
次の関係式を用いると
(Eq.9)
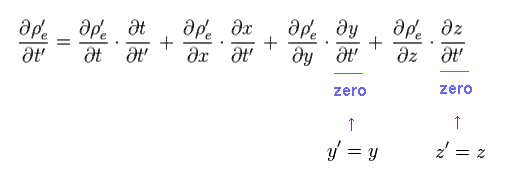
Eq.8 と Eq.9 から、次を得る。
(Eq.10)
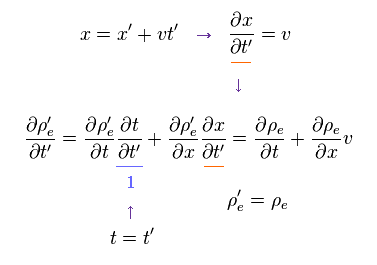
Eq.7 の右辺の最初の式は
(Eq.11)
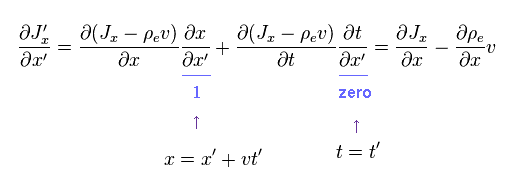
Eq.10 と Eq.11 を Eq.7 に代入して、次を得る。
(Eq.12) 古典力学 = OK.
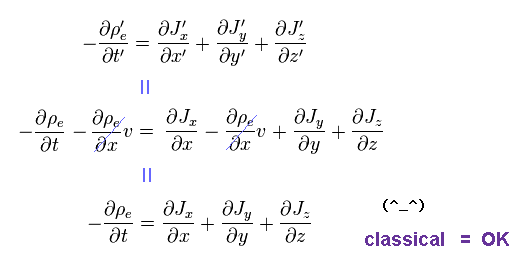
結果的に、 古典力学の あらゆる慣性系において、電荷と電流間の 正常な関係式が 保たれることが分かる。
重要な点は 次のような項が 最終の式に含まれてはならないということである。
(Eq.13)
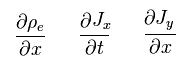
なぜなら Eq.13 に示した項は 他の項と 独立して 色んな値をとれるからである。
つまり Eq.13 の項が Eq.7 に含まれると この式自体が壊れてしまうことになる。
(Eq.7)
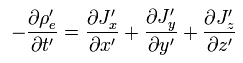
次に 相対論のケースについて考える。
(Eq.14)
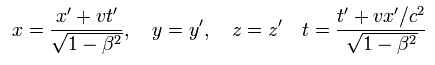
Eq.14 の関係式 (= ローレンツ変換 ) を用いると、 Eq.7 の左辺は 次のように表せる。
(Eq.15)
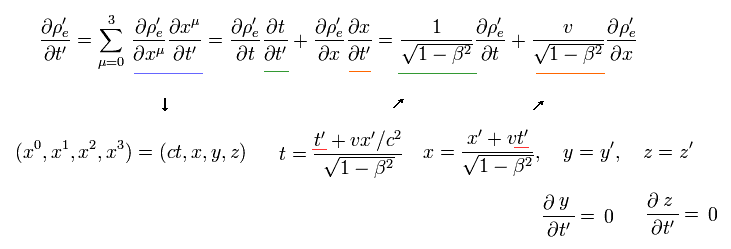
位置座標 ( x', y', z' ) は S' 系のある特定の地点を指定したもので 時間変数 t' とは独立なものである。
そのため t と x の変数のみ t' を含んでいるのでゼロにならない。
同じように、 Eq.7 の右辺の最初の項は、
(Eq.16)
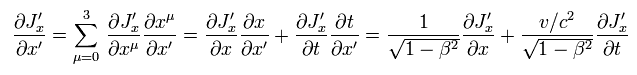
Eq.7 の関係式を ローレンツ変換で不変にするには、電荷と電流密度を 4元ベクトルとして定義する必要がある。
(Eq.17)
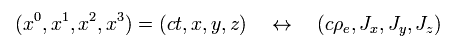
つまり ローレンツ変換のもとで、電荷と電流密度は 次のように変換する。
(Eq.18) ローレンツ変換。
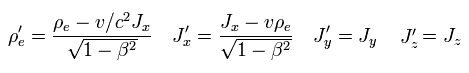
Eq.18 を Eq.15、Eq.16、 Eq.7 に代入すると、次を得る。
(Eq.19)
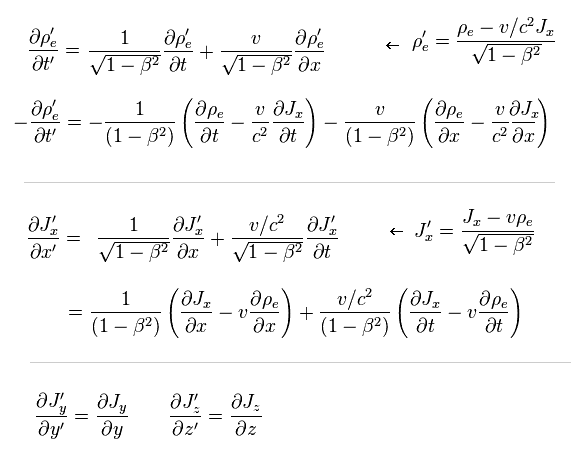
つまり、
(Eq.20)
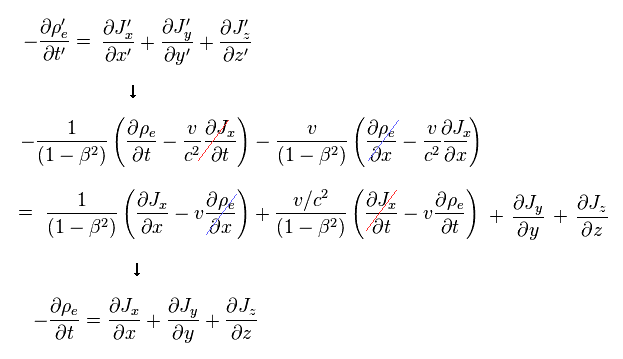
Eq.4 の式を得ることができた。
結果的に、特殊相対論は 電磁気学において Eq.18 のローレンツ変換を必要としていることになる。
Eq.18 は もとの電荷密度がゼロ ( ρe = 0 ) のときでさえ、ローレンツ変換によって 新しい奇妙な電荷 ( ρ'e ) が 中性の 電流 ( Jx ) から生成される (= Eq.21 ) ことを意味している。
(Eq.21)

結果的に この変換は Fig.41 のような 致命的なパラドックスを引き起こすことになる。
(Fig.41) 特殊相対論における パラドックス。

(Eq.22) ローレンツ変換。
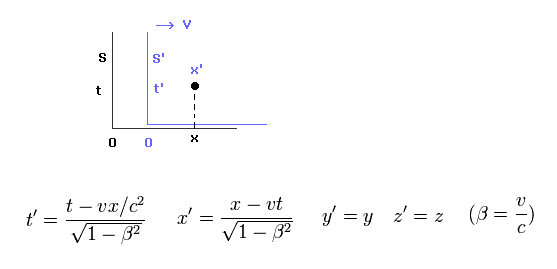
上のセクションのように S' 慣性系が 速度 "v" で x 方向へ動いている。
時間と空間のローレンツ変換を Eq.22 に示す。
(Eq.23) 電場 (= E ) と 磁場 (= B ) のローレンツ変換。
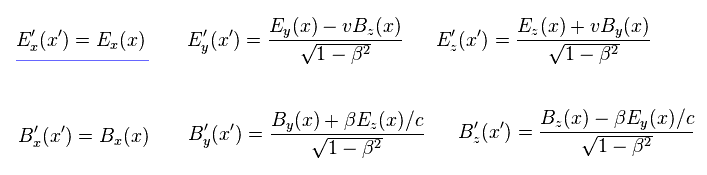
あるウェブサイトか何かで 電磁場のローレンツ変換を探してみるとお分かりになると思うが、Eq.23 のようになる。
重要な点は 青線で示したように 移動方向の電場 (= Ex ) は ローレンツ変換で 変化しないしないということである。電線内に 新たな電荷が発生してもである。( ← ここがおかしい。 )
これは 明らかに致命的なパラドックスである。
最初の Ex がゼロだと、ローレンツ変換後の E'x はゼロのままということになってしまう。
ここでは この変換を ベクトル (= A )、スカラー (= φ ) ポテンシャルから導出する。
(Eq.24) ベクトル・スカラーポテンシャル。

電磁気学では、電磁場は 電気 (= スカラー )、磁気 (= ベクトル ) ポテンシャルで表される。
もちろん このページに示したように、これらのポテンシャルは 相対論と電磁気学の融合のためだけに 人為的に導入されたものである。
マクスウェル方程式が 特殊相対論を満足するには、これらの A や φ は ローレンツ変換の下で 次のような変換式に従う必要がある。
(Eq.25) ベクトル (= A ) と スカラー (= φ ) ポテンシャルのおける ローレンツ変換。
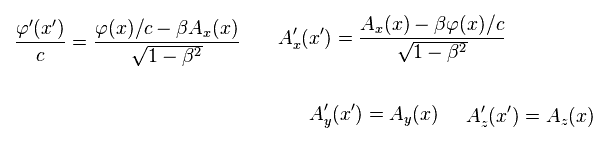
Eq.25 と ローレンツ変換の基本式を用いて、Eq.23 の関係式が得られる。
(Eq.26) 定常な電流 J → 磁場 B。
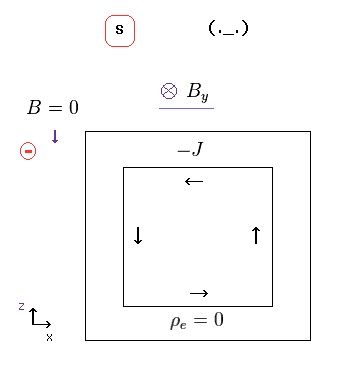
Eq.26 の S 系 (= 静止系 ) では、電流 J は 定常であり、それは 定常な (= 静的な ) 磁場 B を発生する。
重要な点は Eq.28 のビオ・サバールの法則により、上部の電線内の 電流 J は 外部の負電荷の位置に磁場を起こさないということである ( 外積の関係でゼロになる )。
(Eq.27)
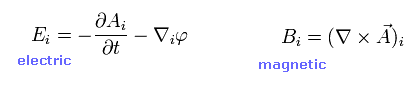
電磁場は Eq.27 に示したように、ベクトル、スカラーポテンシャルを用いて表される。
また 電流 J と 磁場 B (= ベクトルポテンシャル A ) の間の関係式は
(Eq.28)
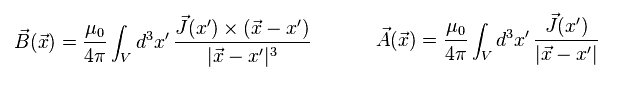
ビオ・サバールの法則によれば、磁場 B は 電流 J を用いて表される。
Eq.28 に示したように、電流方向の延長にある位置での 磁場は 外積の式により ゼロになる。
つまり Eq.26 の負電荷の位置では 上部の電線からの 磁場 B は 必ず ゼロになる。
(Eq.29)
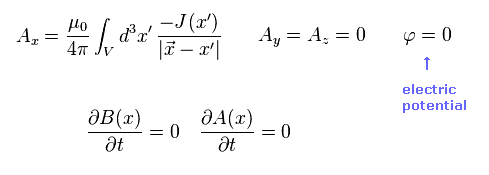
Eq.26 から、静止系 (= S ) における ベクトル、スカラーポテンシャルは Eq.29 のようになる。
Jx のために ベクトルポテンシャル Ax のみ ゼロでない。
(Eq.30)
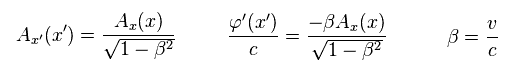
Eq.29 を Eq.25 のローレンツ変換に代入して Eq.30 を得る。
ここで 次のローレンツ逆変換を用いる。
(Eq.31)
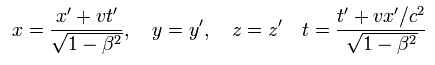
Eq.27、 Eq.30、Eq.31 から、 ローレンツ変換後の E'x は Eq.32 に示したように ゼロのままであることが分かる。
(Eq.32) ローレンツ変換の下で Ex = 0 → E'x = 0。
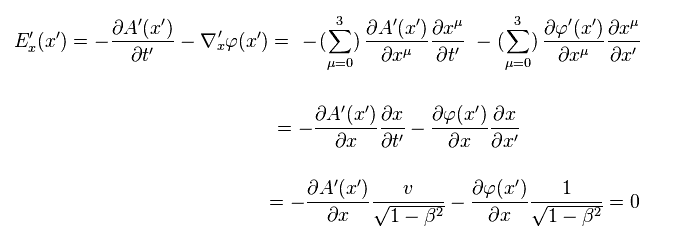
結果的に Fig.41 と Fig.42 のパラドックスが起きてしまう。
Fig.42では、上部の電線内で 新たな電荷が発生し、奇妙なことに その x 方向のみの電場が ゼロになってしまう。
( y、z 方向の電場は ゼロでないのにである。 )
これは 完全にパラドックスであり、これらが非常におかしな電荷達であることを示している。
電線内の これら新たに発生した電荷が z と y 方向のみ電場を起こす
( しかし x 方向には 電場は 起こさない )。
つまり この z 方向の電場は Eq.33 と Eq.34 に示したように 磁気ローレンツ力をキャンセルできる。
( S' 系では 外電荷が 速度 "v" で 動き始めるため 磁気ローレンツ力が発生する。)
(Eq.33)
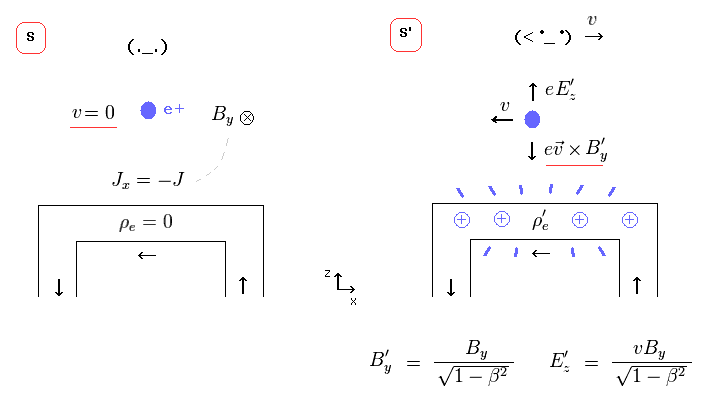
(Eq.34)
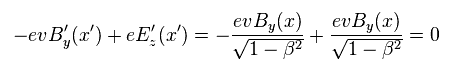
ご覧の通り、相対論的な電磁気学 ( ローレンツ力 ) は 電流 J に垂直な方向のみ 有効な理論なのである。
平行な方向では 特殊相対論は 完全に破綻している。
Fig.41 で 何らかの磁気力が 電気力をキャンセルできるかもしれないと考えている人がいるが、それはできない。
Eq.28 の ビオ・サバールの法則によれば 上の電線からの磁場は 外電荷の位置ではゼロになるからである。
たとえ 何らかの磁場があったとしても その外電荷が 非常にゆっくり動けば S' 系でのみ 新たにできた電荷を有する電線方向へ移動できてしまう。
これは 明らかにパラドックスである。

2014/5/22 updated This site is link free.