トップページ (2電子原子も含む正確な新ボーア模型)
電子スピンは幻想である。
このページで、我々は シュレディンガー方程式が ボーア・ゾンマーフェルト模型に属し、かつ シュレディンガーの水素原子が 間違った 非現実のものであることを証明した。
ここでは、シュレディンガーの水素原子を もっと厳密に評価することにする。
最初に、シュレデインガー自身は マックス・ボルンが提唱した シュレディンガー方程式における確率密度の概念に反対していた。
シュレディンガーは コペンハーゲン解釈をベースにした量子力学に強い不快感を持っていたアインシュタインに似た考えの持ち主だった。
そのため シュレディンガーは "ジグザグ運動する電子" のような新しいモデルを考案しようとしていたが成功しなかった。
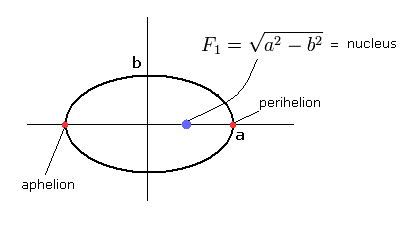
(Fig.1) ボーア・ゾンマーフェルトの”楕円形”の水素原子。

ボーア・ゾンマーフェルトの水素モデルでは、運動エネルギー (T), クーロンエネルギー (V), 全エネルギー (E) の関係は、
(Eq.1)

(もちろん、この関係式は シュレディンガーの水素原子と同じである。)
ボーア・ゾンマーフェルトの量子化条件の”動径”部分は、
(Eq.2)

もし、運動量 (pr) を次のように仮定すると、
(Eq.3)

(ここでは、 λr は、”動径方向の”ド・ブロイ波長である。)
Eq.2 は次のように表せる。
(Eq.4)

Eq.4 は 軌道1周に含まれる 動径部分の長さが ド・ブロイ波長の整数倍 (nr) であることを意味している。
ここで、運動量 (pr) を次の演算子で置き換える。
(Eq.5)

次の波動関数 (ur) を用いると、
(Eq.6)

次を得ることができる。
(Eq.7)
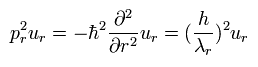
Eq.7 は Eq.3 に等しい。
Eq.6 は 波長が λr の波動関数を意味している。
普通は、運動量 (pr) や λ は 各 r で変化する。つまり 波長 λr は r の関数である。
微小区間内では、Eq.6 の 波長 λ が 定数であると見なすことができる。
そのため、Eq.4 は 次のように 微小区間に分割できる。
(Eq.8)
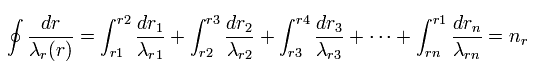
Eq.1 の関係より、水素原子の電子は 1平面のみに属している (例えば、x-y 平面) ことが分かる。
(Fig.2) 水素の電子は 1平面のみに属している。

もし、x-y 平面を ある地点における 電子の運動量ベクトルと 原子核を含む面に設定すると、運動量のz成分 pz はゼロになる。
( 全地点において、このような x-y 平面を定義できる。)
(Eq.9)

Fig.2 では、クーロン位置エネルギー (V) は、
(Eq.10)

そのため 次のように 位置エネルギーの z方向の傾きがゼロになる。
(Eq.11)
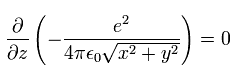
これは 運動エネルギーの z成分が保存する ことを意味する。
運動量のz成分の初期値がゼロであるため、水素原子の電子は必ず x-y 平面に属することになる。
(シュレディンガーの水素原子は この基本的なルールを少し破っている。このことは後で説明する。)
1平面における x と y 方向は "動径方向" と "接線方向" に置き換えることができる。
(もちろん、3次元の系においても、動径方向と接線方向の部分に分離できる。)
残りの量子化条件は
(Eq.12)

もし、”接線方向”の運動量を "接線方向"の波長に置き換えると、Eq.12は 次のようになる。
(Eq.13)

ここでは、次の接線方向の波動関数を使用する。
(Eq.14)

Eq.14 は 接線方向の軌道1周が 1波長であることを意味している。
つまり、半径 r の軌道において、接線方向の軌道1周は 次の波長1つ分となる。
(Eq.15)
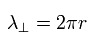
Eq.14 の波動関数と 接線方向の運動量演算子を使うと、次を得る。
(Eq.16)

よって Eq.15 が成り立っている。
結果として、"古典的な" ボーア・ゾンマーフェルトの関係式 Eq.1 は 波動関数と 運動量演算子を用いて 次のように表すことができる。
(Eq.17)

Eq.17 の形は シュレディンガー方程式と同じである。
ボーア・ゾンマーフェルトとシュレディンガー方程式の両方において、波動関数は 互いに垂直な "動径方向" と "接線方向" の部分に分離できる。
上の3つの条件 (Eq.1, Eq.4, Eq.13) を満足する 全エネルギー値 (E) は 1つのみしかない。
(詳細な計算方法については、このページ を参照のこと。)
(Eq.18)
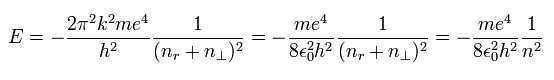
ここで、
(Eq.19)

Eq.18 のエネルギー解は シュレディンガーの水素とちょうど同じである。
次に 上の3つの条件 (Eq.1, Eq.4, Eq.13) を満足する エネルギー値がどうして1つしかないのか説明する。
Eq.1 より、動径方向の運動エネルギーは
(Eq.20)

つまり 動径方向の運動量 (pr) は、
(Eq.21)

全角運動量の平方値 (L2) は、ボーア・ゾンマーフェルトとシュレディンガーの水素原子の両方において 保存する。
ボーア・ゾンマーフェルト模型では、L2 の値は Eq.12 (もしくは Eq.13) の量子化条件から得ることができる。
シュレディンガー方程式においても、”定常な”L(L+1) の 全角運動量 L は Eq.12 の条件から 決定される。これについては後で説明する。
また、Eq.21 は すべての r における動径方向の条件を含んでいる。
未知の定常値 E は、Eq.21 を 残りの量子化条件である Eq.2 (もしくは Eq.4) に代入することによって 決定できる。
よって、3つの式 (Eq.1, Eq.4, Eq.13) を基に、我々は Eq.18 のエネルギー値を1つ得ることができる。
Eq.21 から、各 r における 動径方向の運動量 ( pr ) は E と L2 が保存されるとき、決定することができる。
(これは ボーア・ゾンマーフェルトとシュレディンガーの両方の水素において、”動径方向”の波動関数が 決定されることを意味する。)
また、運動量 (もしくは 波動関数)は 連続している。
もちろん、接線方向の運動量も次のように決定される。
(Eq.22)

Eq.21 と Eq.22 より、各 r における 運動量ベクトルが決まることになる。
束縛状態では、原子核から離れていった電子は、また戻ってくる必要がある。
これらの事実より、水素原子の軌道は Fig.3 に示すように "閉じている" ことになる。
(Fig.3)

水素原子のシュレディンガー方程式は、
(Eq.23)

これは Eq.17 と同じである。
シュレディンガー方程式では、次の 極座標を使う。
(Eq.24)
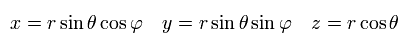
例えば、x による偏微分は次のように表せる。
(Eq.25)
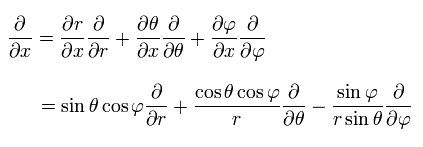
Eq.23 は 次に等しい。
(Eq.26)
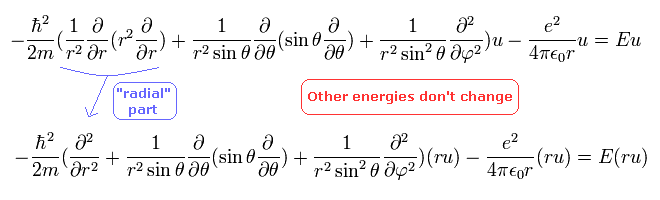
2行めは、"u" の代わりに "ru" 用いることで、動径部分がより簡潔な形になっている。
波動関数 "ru" は、次のように "動径方向" と "線線方向" に分離できる。
(Eq.27)

Eq.27 を Eq.26 の2行目に代入して、Eq.26 を次で割ると、
(Eq.28)

次の式が得られる。
(Eq.29)

ここで α は 定数である。
Eq.29 から、Eq.26 を 次のような "動径方向" と "接線方向" の式に分離することができる。
(Eq.30)

と、
(Eq.31)

Eq.26 から 次の 接線方向の運動エネルギーをピックアウトする。
(Eq.32)
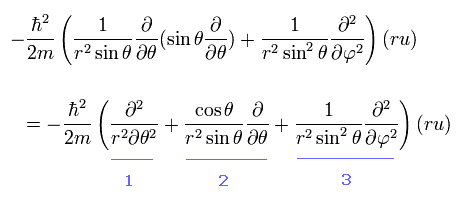
Eq.32 の ”1”番目の項が θ 方向の 運動エネルギーであることは 容易に理解できる。
また Eq,32 の "3"番目の項は θ が 90°に固定されているとき φ 方向の運動エネルギーを表す。
(Eq.33)
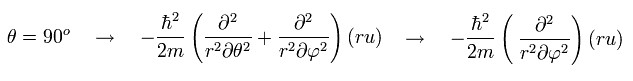
θ が 90°に固定されているとき、 Eq.32 の 奇妙な "2" 番目の項は消える。 ( cos 90o = 0)
ボーア・ゾンマーフェルト模型と比較するには、Eq.17 と Eq.23 において、1つの面のみを選ぶのが適切である。
Eq.32 に示すように 変数 θ は この目的には 不適切である。
変数 φ が適している。しかし θ を 90°に固定する必要がある。(Eq.33)
(Fig.4)
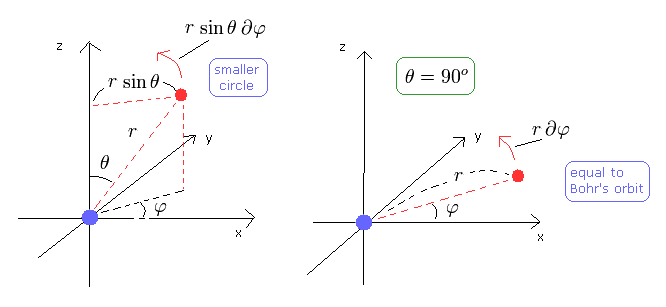
Fig.4 の左の図は、θ が 90°以外のときである。
この場合は φ 方向の円は ボーア軌道より小さくなり、よって φ 方向の運動エネルギーも小さくなる。
その不足部分を補うために、θ が 90°以外のとき、Eq.32 の "2"番目の項が重要になる。
そのため、各 l において、z 方向の角運動量が 最大になる場合を考える。(例えば、l=2, m=2 )
(Eq.34) ( l=1, m=1 ) ( l=2, m=2 ) ( l=3, m=3 ) などの場合。

Eq.34 の場合では、水素原子の軌道は x-y 平面に属してなければならない。
つまり、基本的には これらの球面超調和関数には 変数 θ が含まれていてはいけないのである。
しかし、シュレディンガー方程式は この事実を 無視しているため、全角運動量が少し大きくなっている。 (= L(L+1) )
( Lの 2乗が ボーア・ゾンマーフェルト模型のように L2 になるのは しごくあたりまえの話ではあるが・・。)
Eq.34 では、シュレディンガー方程式の解に θ = 90°を代入した。
もちろん、解を得る前に シュレディンガー方程式の Eq.31 に θ = 90°を代入しても、次のように同じ結果にたどりつく。
(Eq.35)

(Eq.36) Eq.35 の解

Eq.34 もしくは Eq.36 と同じ結果は x-y 平面に属しているとした ボーア・ゾンマーフェルト模型からも得ることができる。
(この場合は、Eq.17 の解 u は x と y の関数 (z でなく) となる。)
結果として、Eq.34 の量子化条件が満足されているとき、ボーア・ゾンマーフェルトの量子化条件も満たされていることを意味している。
(よって、エネルギー値を決定する 重要な3つの条件のうち1つが シュレディンガーとボーアの水素原子で 共通であることが証明された。)
角運動量ベクトルが他の方向を向いているときも、同じ l のときは "接線方向"の運動エネルギーは共通の値となる。
つまり、それらの状態のうち1つが、ボーア・ゾンマーフェルトの量子化条件と等しいとき、それは 他の状態にもあてはまることになる。
ボーア・ゾンマーフェルトの水素においても、角運動量ベクトルが 様々な方向を向いた いろんなパターンがあることはいうまでもない。
もちろん、それらは 共通のエネルギー値をもつ。
そのなかで、代表として x-y 平面に属した軌道を考えるのが もっとも簡単な方法である。
例えば、l=2 の場合、球面調和関数は 必ず sin2θ や cos2θ などの θ 方向に 2 ド・ブロイ波長 のものを含む。
しかし すでに述べたように、θ 変数は φ 方向と違って 少し やっかいである。
Eq.32 の ”1”番目の項は θ 方向の”本来の”角運動量(と接線方向の運動エネルギー)を与える。
しかし、Eq.32 は 水素原子解が φ の変数を含んでいないとき (m=0) のときでさえ、いわゆる "アーチファクト" (2番目の項)を含んでいる。
このことは、全角運動量の2乗の値が L2 でなく L(L+1) であるという 奇妙な現象を起こす原因である。
本来なら、m=0 のときは、Eq.32 の "2"番目の項を消去する必要がある。 (しかし、またここでもシュレディンガー方程式は本来の事実を無視している。)
シュレディンガーの解 χ (= rR ) は Eq.30 もしくは Eq.37 に示すように "動径方向"の運動エネルギーを含んでいる。
(Eq.37)

これらの シュレディンガーの解は
(Eq.38)

ここで r0 は "ボーア半径" である。
例えば、nr = 1 のとき、”動径方向”の運動エネルギーの大きさが "1" を意味し、動径方向の軌道1周が次のように 1ド・ブロイ波長である。
(Eq.39)

これらはいわゆる "波の位相" で、 ド・ブロイの関係式を満足する。
nr = 2 のとき、これは ”動径方向”の運動エネルギーの量が "2" であることを意味しており、動径方向の軌道1周が 次のように 2ド・ブロイ波長である。
(Eq.40)

nr = 3 のとき、これは "動径方向"の運動エネルギーの量が "3" を意味し、次のように ”動径方向”の軌道1周が 3ド・ブロイ波長である。
(Eq.41)

Eq.34 と Eq.38 から、Eq.18 のボーア・ゾンマーフェルト模型と同じ エネルギー準位を得ることができる。
例えば、n=1 のエネルギー準位では、シュレディンガーの解は 角運動量を持たない (l=0)。しかし "動径方向" の運動エネルギーを持つ。( nr= 1, ).
一方で、n=1 のボーア・ゾンマーフェルト模型では、角運動量が1 (l=1) で、動径方向の運動エネルギーがゼロである。( nr = 0 ).
結果として、それらの合計は Eq.18 と Eq.19 によれば 両方のケースで 1 となる。( n = 1 + 0 = 0 + 1 = 1 )
(Eq.18)
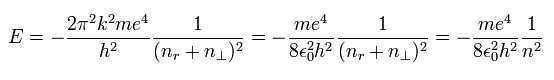
ここでは
(Eq.19)

そのため、同じ n において、シュレディンガーとボーア・ゾンマーフェルトの水素は同じになる。(Eq.42)
(Eq.42) シュレディンガー = ボーア・ゾンマーフェルト。

次に シュレディンガーとボーア模型において、動径方向の量子化条件が同じであることを証明することにする。
(Fig.5) "動径方向の" ド・ブロイ波 (= 位相)。
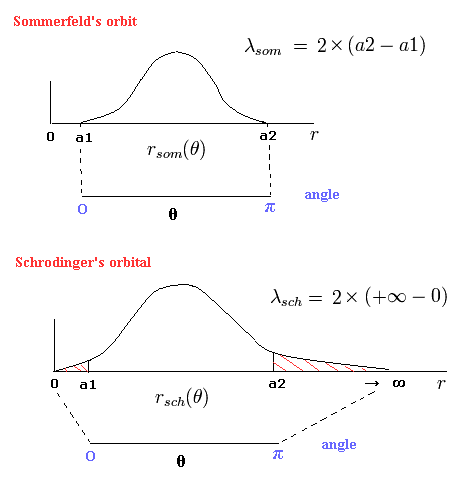
Fig.5 の 上の図は ボーア・ゾンマーフェルト模型における 半周軌道が 0.5の”動径方向の” ド・ブロイ波を含んでいる。
(そのため、軌道1周には 1 × ”動径”の ド・ブロイ波を含んでいる。(= 動径方向に 1ド・ブロイ波長。))
Fig.6 に示すように a1 と a2 は それぞれ 近位点と遠位点である。
(Fig.6) ゾンマーフェルトの 2S "楕円形"軌道 ( Fig.5の上図 ).
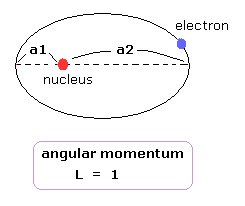
そのため、Fig.5 の上図は 次のように表せる。
(Eq.43)

Fig.6 に示すように 近位点と遠位点において、
そのため、Fig.5 の上図の両端では、傾きがゼロ (= λ が無限大。) になる。
実は、変数変換によって、Fig.5 の上図 (= ゾンマーフェルト模型)が Fig.5 の下図 (= シュレディンガーの解)に等しいことを証明することができる。
ここで これについて説明することにする、
Eq.43 で、次のように変数 r を r' に変換する。
(Eq.44)
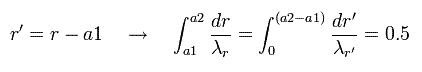
Eq.44 は Eq.43 の "平行移動" である。
さらに 変数を次のように変化させる。
(Eq.45)

また r'' を r 表記に戻す。
(Eq.46)
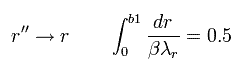
ここで β は "任意" の値である。
Eq.45 は 図そのものの 拡大 もしくは 縮小 を意味している。
次のように β が無限大のとき、
(Eq.47)

Eq.47 は Fig.5 の下図 (= シュレディンガーの”動径方向”の解。) となる。
このことは ボーア・ゾンマーフェルトの”動径方向”の量子化条件は Fig.5 の シュレディンガーの解とちょうど同じことを意味する。
正確には、ゾンマーフェルトの動径方向の軌道を微小区間に分割して、各区間をそれぞれ 適切に 平行移動と拡大する必要がある。
この方法 (= 変数変換, Fig.7 も参照) によって、我々は ボーア・ゾンマーフェルトの量子化条件が シュレディンガー方程式の条件と同じであることを証明することができた。 (Fig.7)
(Fig.7) 変数変換。

しかし、1つ注意しなければならないことがある。
Fig.5 の ゾンマーフェルトの動径方向の波の位相の 端においてのみ、波長は 無限大である。
これは 両端において 動径方向の運動量がゼロであることを意味する。
(Eq.48 もしくは Fig.7 の "境界の"状態 (boundary state) を参照のこと。)
我々は 上記の平行移動や拡大 (もしくは縮小) などの方法で これらの”無限大”の波長を ”有限の”波長に変化させることはできない。 (Eq.49 参照)
(Eq.48) 両端で 波長は無限大である。
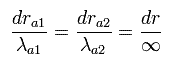
(Eq.49) 境界の状態を変えることができない。

そのため、同じエネルギー値を得るには、ゾンマーフェルトとシュレディンガーの波動関数の両方における境界状態が同じである必要がある。
幸運なことに、シュレディンガーの動径方向の波動関数の全部の境界の状態は Eq.39 や Eq.40 に示すように 無限大の波長を持つ。
例外は 1S (rR10), 2S (rR20), 3S (rR30) などである。
これらの状態では、角運動量がゼロ (l=0) であるため、原点において 動径方向の運動量が無限大になる。
(運動量は r の 平方根に反比例する、そのため その傾きは ゼロでない 有限値となる。)
もし、ボーア・ゾンマーフェルト模型が この ゼロ角運動量の軌道をもつとしたら (これはつまり 回転のかわりに 振動を意味する)、これらの状態は シュレディンガーの "S" の波動関数とまったく同じになるだろう。
なぜなら これらの両方とも同じエネルギーの関係式を満たすからだ。
(もちろん、角運動量がゼロの状態は "非実在"であることはいうまでもない。なぜなら電子が原子核にぶつかってしまうからだ。)
結果として、シュレディンガーの波動関数は 同じエネルギーを与える ボーア・ゾンマーフェルト軌道と同じ 3つの条件 (Eq.1, Eq.2, Eq.12) を満足する。
-----------------------------------------------------------------------
ところで、Fig.5 の ゾンマーフェルトの動径方向のド・ブロイ波の位相を別の図で表現することは可能だろうか? (Fig.8 の赤い線)
(Fig.8) ゾンマーフェルトの波の位相。
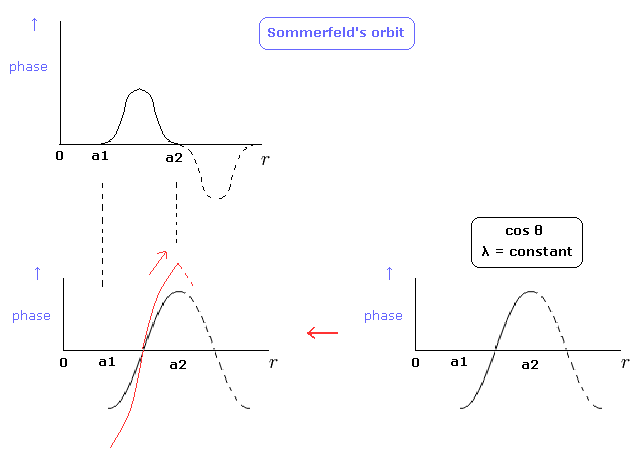
Fig.8 の下図は、a1 と a2 地点における傾きが ゼロではない。
"本来の" コサインカーブが ゼロの傾きを持つため、これらの地点の λ を無限大にするには 傾きはゼロになってはいけない。
そのため、これらの地点での傾きは 不連続になり、これは位相の変化が無限大になることを意味する。
結果として Fig.8 の下図を ゾンマーフェルトの動径方向の波の位相として選ぶのは不適切である。
-----------------------------------------------------------------------
このページで どうして シュレディンガー方程式が間違っているかを説明した。
もう一度、これらの理由をまとめることにする。
(Fig. 9) シュレディンガーの 2P 動径波動関数 (角運動量 = 1).
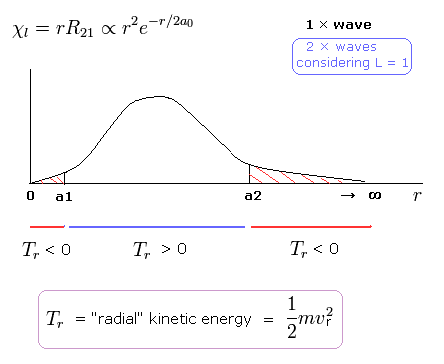
Fig.9 に示すように 2P の動径波動関数 ( χ = rR21 ) は マイナスの運動エネルギーの部分を含んでいる。 ( r < a1, a2 < r ).
そのため、”実在する”ボーア・ゾンマーフェルト模型では、電子の軌道半径 (r) は ある”下限値”( a1 ) よりも 短くなることはできない (Fig.6)。
ただ、これはもちろん角運動量がゼロでないときの話である。
(角運動量が非現実的にゼロのときは、電子は振動しているため ”理論的には”半径 r はゼロに近づくことができる。)
しかし、上で述べたように、シュレディンガー方程式の確率密度は ゼロから無限大にならなければならない。
奇妙なことに、r < a1 の範囲では、シュレディンガーの動径方向の運動エネルギーは マイナスになってしまうのである。( 1/2 mv2 < 0 ! )
シュレディンガー方程式 においても、ケプラーの法則(面積速度一定の法則)を満たし、これはすなわち 各軌道で 角運動量 (L) は定数になることを意味する ( L = 0, 1, 2, ... )。
つまり、”接線方向”の運動エネルギーはマイナスになることはできず、かわりに ”動径方向”の運動エネルギー ( Tr ) が わりを食って マイナスになってしまうのである (Fig.9)。
(なぜなら r がゼロに近づくにつれて、”接線方向”の運動エネルギーが 無限大に近づいていくからである。)
半径 r が a2 よりも大きいとき、クーロン位置エネルギーは ある上限値よりも 高くなる。
この領域では、全エネルギー (E < 0) を一定に保つためには、動径方向の運動エネルギーがマイナスにならなければならない。
これらの理不尽で非現実な状態が シュレディンガー方程式が間違っていることを示している。
しかし、どうして シュレディンガーの原子の確率密度の範囲は ゼロから無限大にしなければならないのであろうか?
例えば、ヘリウム原子においては、シュレディンガー方程式の変分法は 具体的な軌道イメージを与えることはできない。
そのため もちろん境界状態がどうなっているかも分からない。
よって、便宜上 確率密度の範囲を ゼロから無限大にするしか方法がないのである。
このことは、1S, 2S, 3S などのゼロの角運動量を持つ "非現実"な状態を生じさせる原因となる。
もし、動径波動関数が定数だとすると、全空間で積分したとき 発散するのを防ぐには、その定数は ゼロにならなければならない。
そのため シュレディンガーの波動関数は必ず 定数でない 動径波動関数を含んでいる必要がある。
結果として、n=1 のエネルギー状態では 角運動量のかわりに nr が 1 になる必要がある。
シュレディンガーの水素原子で、”実際の”電子の運動範囲を 上記のゼロから無限大よりも小さくすることはできない。
この場合は、電子の運動の途中で ”動径方向”の波の位相が 不連続になってしまう。
そのため シュレディンガーの電子は ゼロから無限大へ移動し、そしてまた 向きをかえて戻る必要があるのである。

2011/7/12 updated This site is link free.