Home page
EInstein relativity is wrong.
Relativistic electromagnetic paradox (5/27/2025).
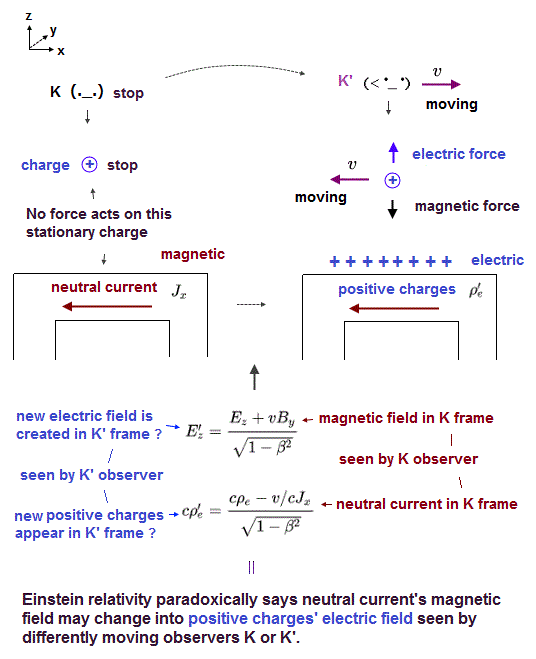
(Fig.1) Lorentz transformation → new charges (= ρ'e ) are generated ↓

According to the special relativity, charge (= ρe ) and electric current (= J ) are NOT constant values.
These transform like spacetime (= ct, x, y, z ) under Lorentz transformation.
See websites, this (p.3) this (p.12) this (p.219).
About the basis of special relativity, see this page, first.
In Fig.1 left, electric wire is neutral (= S ).
But the moment observer starts to move, "positive" charges are generated (= Fig.1 right, S' ) !
(Fig.2) Lorentz transformation of charge (= ρ ) and current (= J ).

Under Lorentz transformation, charge density (= ρe ) and electric current (= Jx ) are mixed ( Fig.2 upper right ).
As a result, even if the original charge is zero ( ρe = 0 ), the neutral current (= Jx ) can generate new charge (= ρ'e ) only in S' frame.
(Fig.3) Lorentz transformation of charge (= ρ ) and current (= J ).

This unrealistic transformation is indispensable for special relativity to agree with Maxwell equation.
As shown on this site (p.12-15), Maxwell equations can keep their form under Lorentz transformation, if upper equation hold.
Light speed "c" is predicted by Maxwell equations.
So special relativity must agree with Maxwell equation with respect to the constant light speed "c".
(Fig.4) Negative charge is attracted toward wire ONLY in S' frame ?

If the upper transformation of charge and current is true, fatal paradox appears.
In Fig.4, a negatively charged particle is at rest outside the electric wire in S frame.
But, the moment the observer moves, the strange positive charges are generated inside electric wire.
As a result, the negative charge is attracted toward the wire, ONLY in S' frame.
This is clearly paradox, which has NOT been solved.
Unfortunately, these kinds of true paradoxes are hidden from ordinary people.
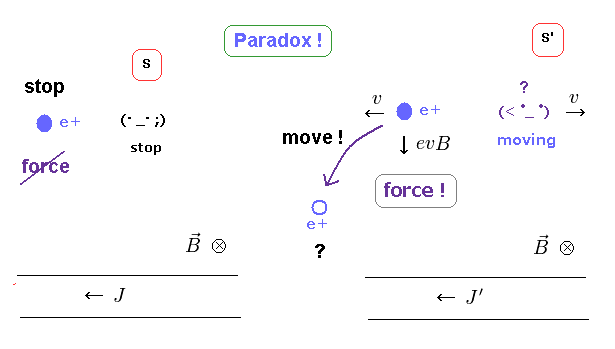
(Fig.5) Lorentz force needs new charges.

Then why new strange positive charges are generated from neutral wire ?
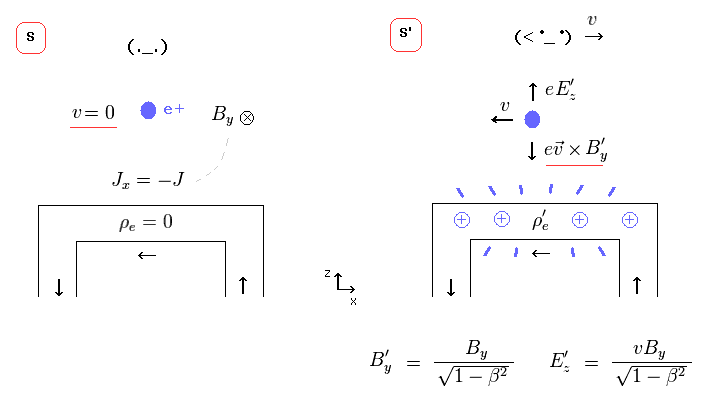
In Fig.5 left (= S ), the observer at rest is looking at neutral wire in which electric current J is flowing.
So, in S frame, electric field E is zero, and the magnetic field B is in y direction.
A positive charge (= e+ ) is at rest in S, so it experiences NO magnetic force.
But while the observer is moving in x direction, the positive charge is moving in the opposite direction from obesrver's viewpoint (= S' ).
This means this charge experiences Lorentz magnetic force, and turns toward wire ONLY in S' frame.
Of course, this is clearly paradox.
To solve this problem, new charges must be generated, and their electric force cancels magnetc force, as shown on this site.
(Fig.6) Magnetic force depends on the charge's velocity.

When a charged particle is moving at velocity "v in the presence of magnetic field B, it experiences the magnetic force ( F = evB ).
The direction of this magnetic force is perpendicular both to the velocity and the magnetic field.
It obeys right hand rule, as shown on this site.
(Fig.7) When the particle is at rest, it feels NO magnetic force.
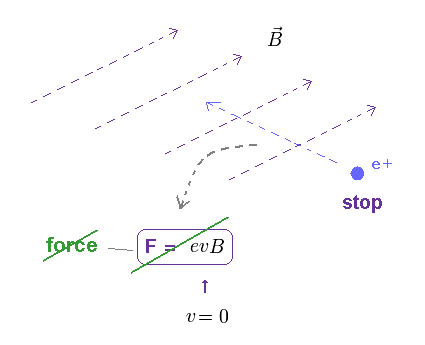
Lorentz magnetic force is given by F = ev×B. ( "×" means cross product. ).
So, when the particle's velocity is zero ( v = 0 ), it feels NO magnetic force.
(Fig.8) When the observer and a charge are at rest in S.
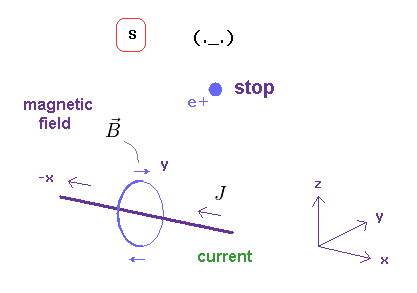
In S frame of Fig.8, a observer and a charge (= e+ ) are at rest.
And there is an neutral electric wire in which the current J is flowing.
The charge's velocity is zero, so this feels NO magnetic force, and keeps stationary.
(Fig.9) From moving observer (= S' ), the charge is moving → magnetic force ?
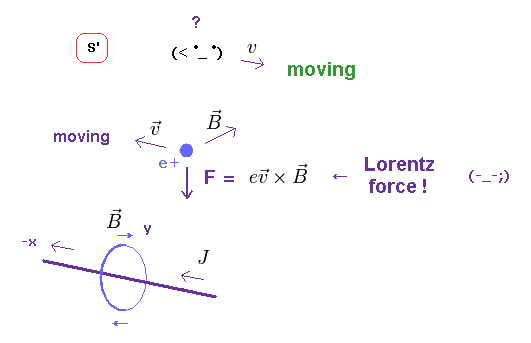
If this observer starts to move (= S' ), the charged particle is moving in the opposite direction from the observer's viewpoint.
As a result, in S' frame, this charge experiences Lorentz magnetic force from current, and is accelerated toward the wire !
This is clearly paradox.
Because this charge is at rest in S frame, but moves toward the wire ONLY in S' frame, as shown in Fig.10.
(Fig.10) When the observer moves, the charge comes closer to the wire !?
Lorentz magnetic force depends on the charged particle's velocity.
This velocity looks different, from the viewpoints of static and moving observer.
This means if Lorentz magnetic law and special relativity is right, the observer has supernatural power to control the particle's motion without touching it !
(Fig.11) Neutral wire changes into "positive" ONLY by observer's motion ?

To avoid paradoxical situation of Fig.10, this neutral electric wire has to produce new positive charges only in S' frame, as shown in Fig.11 right !
(Fig.12)

If the wire gets positive, new electric field (= E ) can cancel magnetic force ( eE = evB in Fig.12 right ).
So, the paradox of Fig.10 can be solved, the relativists insist. See also this and this (p.4).
But this transformation causes another fatal paradox (= Fig.13 ).
(Fig.13) Weak point of special relativity.
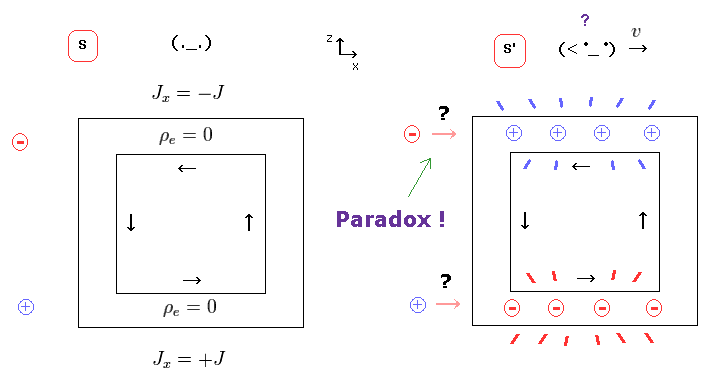
But if a charged particle (= negative ) is at the position of Fig.13, this particle is attracted toward the wire ONLY in S' frame.
Because the electric force acting on this particle cannot be cancelled out by magnetic force.
So depending on the observer's movement, it is determined whether this charged particle is accelerated or not toward the wire.
This is clearly a paradox, and shows special relativity is wrong.
(Fig.14) Magnetic force (= evB ) cannot cancel electric force (= eE ).
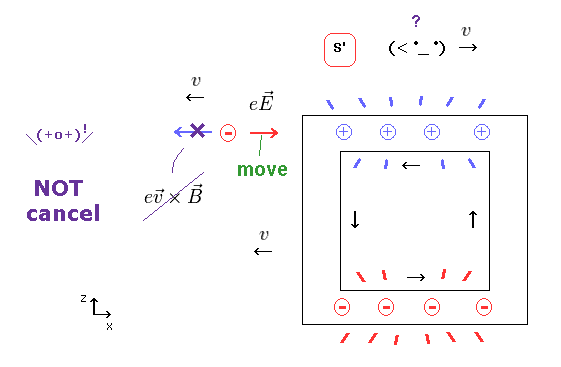
When the observer is moving in x direction, the wire and particle move in minus x direction.
The magnetic force is perpendicular to the particle's velocity.
So this magnetic force (= evB ) is NOT in the x direction, it cannot cancel the electric force (= eE ) in x direction.
As a result, this charged particle is at rest in S, but is accelerated toward the wire in S', which means "paradox".
According to Biot-Savart law, this electric current cannot generate the magtetic field in the x direction.
So there is NO magnetic field at the point of the charged particle.
(Fig.15) Lorentz transformation of electromagnetic fields.

In the upper section, we explain the reason why fatal paradox occurs with respect to charge and current.
If the charge and current transformation is contradictory, the relation of electromagnetic fields should also break down, too.
As shown on this site and this site (p.91), Lorentz transformation of E, B fields become like Fig.15.
E, B fields parallel to the observer's movement do NOT change.
Only E, B fields perpendicular to it transform, and get mixed.
(Fig.16) Electric field E'x is zero, but E'z is NOT zero. ← Paradox !

If Lorentz transformation of Fig.15 is right, strange situation happens.
In Fig.16 left (= S ), electric fields in all directions are zero, only magnetic field B exists.
In Fig.16 right (= S' ), the parellel component, E'x field remains zero.
But E'z is NOT zero under Lorentz transformation.
(Fig.17) ↓ These positive charges are real ?

As you notice, this situation is paradoxical.
The positive charges in the wire generate ONLY E'z ( and E'y ), and does NOT generate E'x.
There is NO such unrealistic charge in this real world.
(Fig.18) Negative charges are removed only in S' frame in relativity ?

If the neutral wire changes into positive one, it means some negative charges are removed from the wire !
It is unbelievable that the observer can remove these negative charge without touching them.
(Fig.19) Observer "teleports" negative charges in special relativity ??

The upper and lower electric wire have the opposite currents.
So in S' frame, the upper wire becomes positive, and the lower becomes negative.
As a result, the total charge in the whole electric circuit is conserved, they insist.
But if this idea is true, this observer has "supernatural" power to teleport charges ONLY by their momevent. This is strange.
(Fig.20) Electrons teleport to the lower wire → repulsive force ?

According to the four-current of special relstivity, minus charges of the upper wire teleport to the lower wire just by simple observer's movement !
In this case, fatal paradox appears as shown in Fig.13.
And as you notice, the state of Fig.20 is very unnatural.
Because the stronger repulsive force among electrons in the lower wire does NOT allow this teleportation.
In any frames, Coulomb law (= Maxwell law ) must be valid.
As a result, special relativity, which contradicts the law of nature, is wrong.
(Fig.21) Observer has NO strange power to teleport charges in real world.

As you feel, it is natural that electrically neutral wire remains neutral irrespective of the observer's movement.
To do so, we have to correct the wrong idea that Lorentz force depends on the observer's velocity, as shown in Fig.8,9.
(Fig.22) Charged particle is moving or not, relative to the "earth".
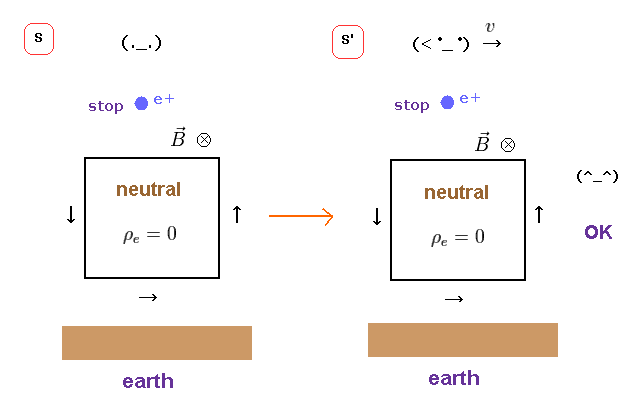
If the observer has nothing to do with Lorentz force law, there must be other factors to determine whether magnetic force is generated or not.
When you look around you, all substances including air are moving with the earth.
When you run fast, you feel wind.
Like this, when the chaged particle is moving relative to the earth (ether), it causes de Broglie waves, and magnetic field around it.
In this case, fatal paradoxes of Lorentz force do NOT happen, and the observer doesn't need to have "unnatural" power.
(Fig.23) "Division" of one electric wire into two ??

The standard relativity explains these strange phenomena from the perspective of the distance between charges, as shown on this site and this site.
In Fig.24 left, this neutral wire contains equal numbers of positive and negative charges.
Only negative charges are moving at speed "v" in x direction in S frame.
When the observer is moving at speed "v" in x direction (= S' ), negative charges appear stationary, and instead, positive charges are moving in -x direction in S' frame.
(Fig.24) Lorentz contraction or rest length between charges ?

According to Lorentz contraction, in Fig.24 left, negative charges are moving, so the spacing between adjacent negative charges is reduced.
As this wire is neutral, the distances between negative and positive changes are the same.
In S' frame, the spacing between negative charges returns to its original rest length.
On the other hand, the distance between positive charges is Lorentz-contracted.
(Fig.25) Distance is Lorentz-contracted → density increases.

In S frame, the rest length between positve charges is l0, and its charge density is ρ+.
In S' frame, the distance between them is Lorentz-contracted, which means charge density increases, as shown in Fig.25 right.
(Fig.26) Lorentz-expanded → negative charge density decreases.

On the other hand, the distance between negative charges is originally Lorentz- contracted in S frame.
When the observer starts to move at the same velocity as these negative charges (= S' ), their distances are expanded (= return to their rest length ).
Because, from the perspective of the obeserver in S', negative charges look stationary.
As a result, the negative charge density decreases in S' frame.
(Fig.27) The wire becomes Lorentz contracted in S' frame.

The electric wire itself is at rest in S frame.
So in S' frame, the length of this wire becomes Lorentz-contracted ( l → l' ), because it is moving in S'.
(Fig.28) Total charge = charge density × wire length.

The total amount of charges is given by charge density (= ρ ) × wire's volume.
From Fig.25 and Fig.27, the total positive charge remains the same in S' frame as in S frame.
(Fig.29) Total negative charges decrease.

From Fig.26 and Fig.27, you find that only the amount of negative charges is NOT conserved.
Because the decrease in negative charge density cannot be cancelled by wire length.
(Fig.30) Neutral wire in S frame.
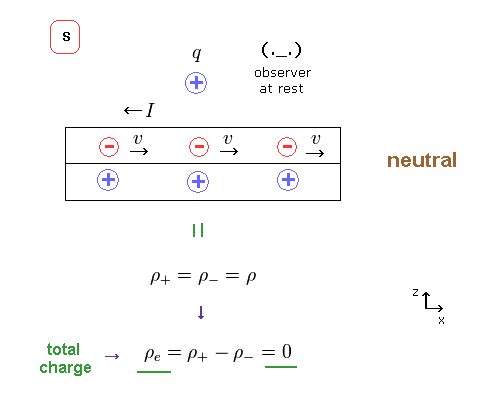
In S frame, we suppose the charge densities of positive and negative are the same.
( ρ+ = ρ- = ρ )
(Fig.31) Net charge density becomes positive in S' frame.

Summing positive (= Fig.25 ) and negative (= Fig.26 ) charges, we find the net charge ( density ) of this wire becomes positive in S' frame, as shown in Fig.31.
(Fig..32) Lorentz transformation of charge and current.

According to special relativity, charge density (= ρ ) and current density (= J ) transform like spacetime (= t, x, y, z ) under Lorentz transformation. See Eq.1.
So these are called "four-current"
(Eq.1) Lorentz transformation of charge (= ρ ) and current (= J ).
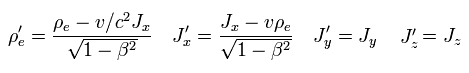
(Fig.33) Electric current J'x in S' frame.

In S frame, the total charge density is ρe = 0 ( neutral ), and the current is Jx = -ρv.
Using Eq.1, we find the electric current (density) J'x is given like Fig.33.
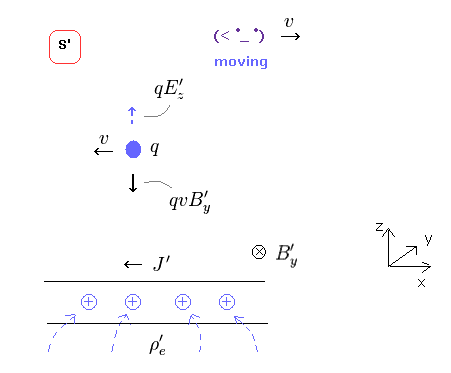
(Fig.34) Electro (= E' ) magnetic (= B' ) fields in S' frame.

The electric field (= E ) produced by line charge is given in this site.
And the magnetic field (= B ) is in this site.
Substituting the results of Fig.31 and Fig.33 into these equations, we can get the electric and magnetic fields around the wire in S' frame, as shown in Fig.34.
(Fig.35) Also in S' frame, z direction of the motion remains zero.
If the z component of the particle's velocity is zero in S frame, it must remain zero also in S' frame.
So, the new generated electric force must be just cancelled by magnetic force in z direction.
( qE - qvB = 0 )
Using Fig.34, we find that the net force in z direction acting on this charged particle becomes cancelled out, and zero, as shown in Fig.36.
(Fig.36) Net force in z direction becomes zero also in S'.
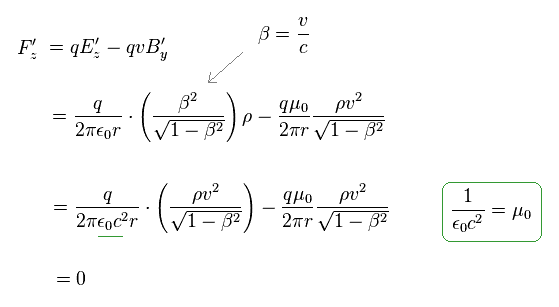
As a result, both in S and S' frames, the net forces in z direction acting on the particle become zero.
So the paradox can be avoided, they insist.
But as shown in Fig.13 and Fig.14, the new electric force in x direction cannot be cancelled out by Lorentz magnetic force.
This direction is the weak point of special realtivity, and proves this theory is wrong.
(Fig.37) Electron charge (e-) is Lorentz-invariant scalar.
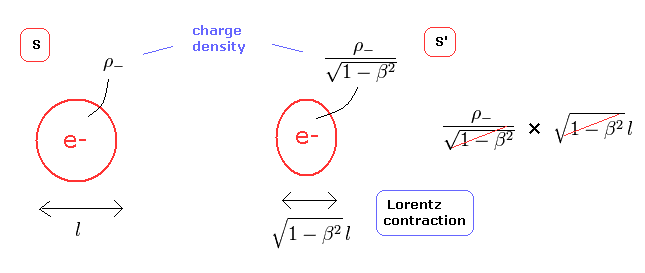
According to the quantum electrodynamics (QED), electron charge (e-) does not change under Lorentz transformation. (= Lorentz invariant scalar. )
Actually, the constant charge "e" is used in the fine structure constant and magnetic moment in QED.
( To be precise, the charge e + permittivity of the vacuum is constant. )
Here we explain this invariance from the viewpoint of classical electromagnetism and special relativity.
The electron is a point particle. But here we suppose the length of the electron is "l", as shown in Fig.37.
From Eq.1 and Lorentz-contraction, the total charge of one electron does not change under Lorentz transformation (= Fig.37 right).
Because even if the length "l" is contracted, the charge density ρ is increased and cancel each other.
(Fig.38) Total charges are conserved in all reference frames.

In Fig.38, the charges and box are moving with S' frame at v with respect to S frame.
In S' frame, two charges (= 2 × q' ) enter box during dt', which means 2q' is increased in the box during dt' (= Fig.38A).
From the viewpoint of S frame, we suppose the charge q' becomes q. ( Actually the charge "e" doesn't change. )
Also in S frame, two charges (= 2 × q ) enter the box during dt, which means 2q is increased in the box during dt.
So in all reference frame, the relation between charge density ρe and current density J must be satisfied.
( When the charge amount of "Q" enters some place per second, charge "Q" is increased per second. It is quite natural. )
(Fig.39) Charge and current densities relationship

In Fig.39, charge density ρe means the electric charge per unit volume, and current density J means an electric current per cross-sectional area.
Considering the movement of the electric charges and the conservation of total charge, the relationship between charge and current densities in the infinitesimal box ( V = Δx Δy Δz ) are
(Eq.2) The relation between the changes of electric current (= J ) and charge density (= ρ ).

The change of electric currents (= J ) in all x, y, z directions causes the change of the charge density (= ρ ) in this box.
Charge density ρe = C / m3 (= coulomb per volume ), current I = C / s (= coulomb per second), current density J = C / s m2 (= coulomb per second per area ).
From Eq.2, we get
As a result,
(Eq.4)

The relation of Eq.4 among charge density and current must hold in all reference frames, when total charge is conserved.
If you believe in the special relativity, the time (= ct ) and space (= x, y, z ) coodinate need to change as four-vector under Lorentz transformation.
( Of course, if we admit "earth ether" instead of special relativity, this strange Lorentz transformation does NOT need to be used. )
(Eq.5)

where S' frame (= x', y', z', t' ) is moving in the x direction at the velocity v with respect to S frame (= x, y, z, t ).
Considering inverse Lorentz transformation, Eq.5 is equal to
(Eq.6)
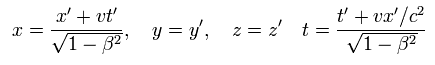
And in any inertial reference frame, the relationship between charge and current density must be satisfied, as shown in Fig.38.
(Eq.7)

To satisfy Eq.7, the charge and current density must change as four-vector like time and space coordinate, which causes "strange" phenomenon as I explained above.
And this leads to breakdown of special relativity in the electromagnetism !
(Fig.40)

First we think about the classical version of Eq.5 upper.
In the classical mechanics, the strange transformation of the time, space and charge do NOT happen.
We need to think only about the natural transformation.
S' frame is movig in the x direction at v, so the current Jx needs to be added - ρe v (= charge density × velocity ) in S' frame.
(Eq.8) Classical mechanics.
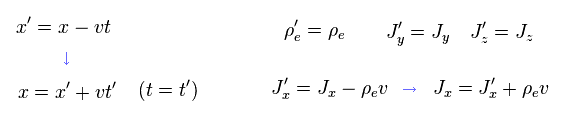
Using the relation of
(Eq.9)
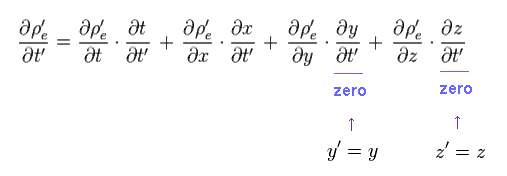
From Eq.8 and Eq.9, we obtain
(Eq.10)

And the first equation of the right side of Eq.7 is
(Eq.11)
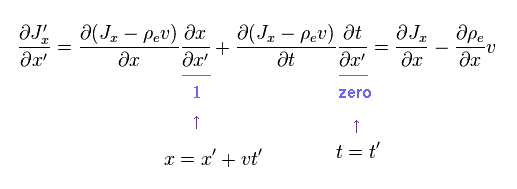
Substituting Eq.10 and Eq.11 into Eq.7, we have
(Eq.12) Classical mechanics = OK.

As a result, in any frames of classical mechanics, the normal relation between charge and current is satisfied.
The important point is that the following terms must not appear in the final equation.
(Eq.13)

Because the terms of Eq.13 are independent from other terms.
( These terms can take any values independently from other terms. )
So if the terms of Eq.13 are included in Eq.7, this equation is broken.
(Eq.7)

Next we think about the relativistic version.
(Eq.14)
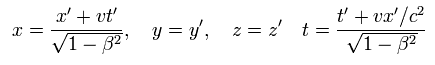
Using the relation (= Lorentz transformation ) of Eq.14, the left side of Eq.7 can be expressed as
(Eq.15)

In Eq.15, the position of ( x', y', z' ) are specified somewhere in S' frame and independent from the time t'.
So only t and x include the variable t' in this case.
In the same way, the first term of the right side in Eq.7 is
(Eq.16)
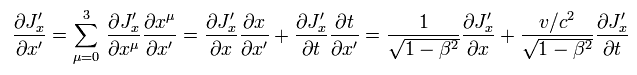
To make the relationship of Eq.7 Lorentz invariant, the charge and current densities need to transform like ( ct, x, y, z ).
(Eq.17)

So, under Lorentz transformation, charge and current transform like
(Eq.18) Lorentz transformation.
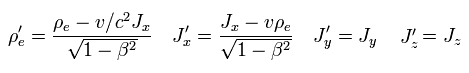
Inserting Eq.18 into Eq.15, Eq.16 and Eq.7, we obtain
(Eq.19)
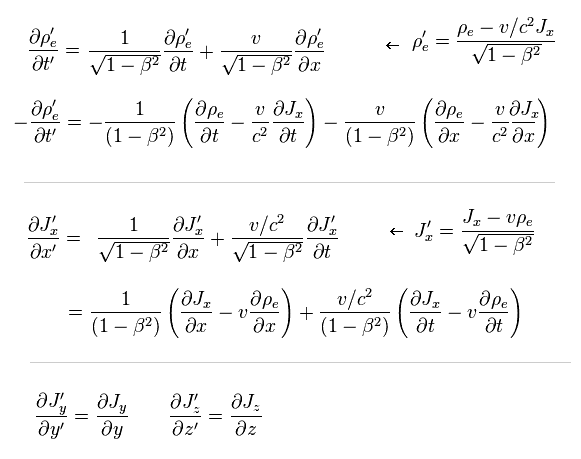
So,
(Eq.20)

We can get original Eq.4.
As a result, the special relativity needs the Lorentz transformation of Eq.18 in the electromagntetism.
Eq.18 means even when the original charge density is zero ( ρe = 0 ), new strange charges ( ρ'e ) are generated from the neutral current ( Jx ) after Lorentz transformation (= Eq.21 ).
(Eq.21)

As a result, this transformation causes fatal paradox of Fig.41.
(Fig.41) Paradox of special relativity.

(Eq.22) Lorentz transformation.

Like in the upper sections, S' frame is moving in the x direction at the velocity of "v".
Lorentz transformation of time and space is as shown in Eq.22.
(Eq.23) Lorentz transformation of electric (= E ) and magnetic (= B ) fields.

If you look for Lorentz transformation of electric and magnetic fields in some websites or something, you will find the transformations of Eq.23.
The important point is that electric field in the moving direction (= Ex ) does NOT change under Lorentz transformation (= blue line ), though new charges are generated inside wire.
This is competely fatal paradox.
When the first Ex is zero, E'x after Lorentz transformation remains zero.
Here we derive this relation from vector (= A ) and scalar (= φ ) potentials.
(Eq.24) Vector and scalar potentials.

In electromagnetism, electric and magnetic potentials are expressed using electric (= scalar ) and magnetic (= vector ) potentials.
Of course, as shown on this page, these potentials are artificially introduced only for unifying relativity and electromagnetism.
For Maxwell's equation to satisfy special relativity, these A and φ must obey the following relations under Lorentz transformation.
(Eq.25) Lorentz transformation of vector (= A ) and scalar (= φ ) potentials.

Using Eq.25 and basic equations of Lorentz transformation, we can get the relations of Eq.23.
(Eq.26) Constant current J → magnetic field B

In S frame (= rest frame ) in Eq.26, the current J is constant, and it generates constant (= static ) magnetic field B.
The important point is that current J in the upper wire cannot generate magnetic field at the position of the external negative charge due to the Biot-Savart relation (= outer product ) of Eq.28.
(Eq.27)
The electric and magnetic fields are expressed using vector and scalar potentials, as shown in Eq.27.
And the relations between current J and magnetic field B ( and vector potential A ) are
(Eq.28)

According to the Biot-Savart law, the magnetic field B can be expressed using the current J.
As shown in Eq.28, the magnetic field becomes zero at the position in the direction of current J due to the outer product.
So at the position of the negative charge in Eq.26, the magnetic field B from the upper wire always becomes zero.
(Eq.29)

From Eq.26, the vector and scalar potentials at the rest frame (= S ) become as shown in Eq.29.
Only vector potntial Ax is not zero due to Jx.
(Eq.30)

Substituting Eq.29 into Lorentz transformation of Eq.25, we get Eq.30.
Here we use the inverse Lorentz transformation of
(Eq.31)
From Eq.27, Eq.30 and Eq.31, we find the electric field E'x after Lorentz transformation remains zero, as shown in Eq.32.
(Eq.32) Ex = 0 → E'x = 0 under Lorentz transformation.

As a result, the paradox of Fig.41 and Fig.42 happen.
In Fig.42, new positive charges are generated in the upper wire, and strange to say, their electric field only in the x direction is zero.
not zero.
This is completely paradox, and these are very strange charges.

These new generated charges inside wire can cause electric field only in the z and y direction ( but not x direction ! ).
So this electric field in z direction can cancel out the magnetic Lorentz force, as shown in Eq.33 and Eq.34.
( An external charge starts to move at the velocity of "v" in S' frame, which causes Lorentz force only in S' frame. )
(Eq.33)
(Eq.34)
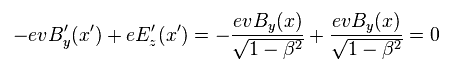
As you see, relativistic electromagnetism ( Lorentz force ) is effective only in the directions perpendicular to the electric current J.
In the parallel directions, special relativity breaks down.
Some people try to think some magnetic field can cancel out the electric force in Fig.41.
But the magnetic field ( from the upper wire ) at the external charge is zero, due to Biot-Savart law of Eq.28.
Even if some magnetic fields are generated, when this external charge moves very slowly, it can come closer to the electric wire only in S' frame, in which new strange charges are created.
This is clearly paradox.

2014/5/21 updated. Feel free to link to this site.