4.5.4　いろいろな最適化　　　　　　　　　　　　目次（第4章）へ

4.5.4.1　整数型最大傾斜法

　前節のような農作業計画で，機械の台数（整数）の組合せを変えて最適化をはかる場合，機械の作業能率についてみるとその値は連続的に変わるのではなくて離散的な値を示している．

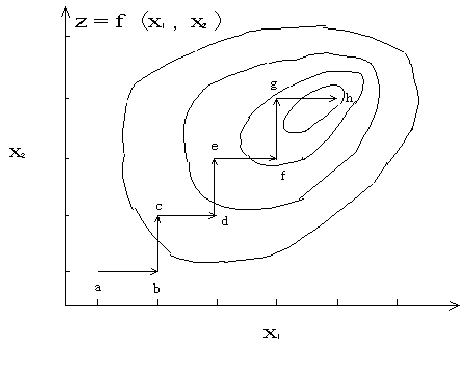
このようにあるシステムz＝（x₁，x₂，…，x_n）において，その要素xiが整数（離散値）であるときその目的関数zを最大にすることを考えると，図4.6のようにある点a（x₁₁，x₂₁，…，x_n1）から出発して，傾斜ベクトル▽f（x₁，x₂，…，x_n）の正の方向の点a_１（x₁₁±1，x₂₁，…，x_n1），点a₂（x₁₁，x₂₁±1，…，x_n1），…，点a_n（x₁₁，x₂₁，…，x_n1±1）のzの値を求め，そのなかで最大値を示す点a_i（図4.6ではb）をめざす．

図4.6　整数型最大傾斜法

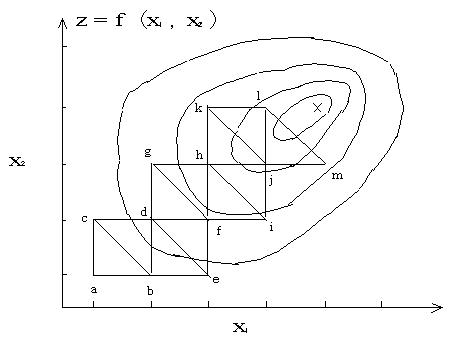
図 .7　整数型山登りシンプレックス法

　同様にして，

　　　f（c）＝max［f（b₁），f（b₂），…，f（b_n）］　　　　　eq. 4.72

となる点cをめざす．

　ここで，b＝（x₁₂，x₂₂，…，x_n2）　　　b₂=（x₁₂，x₂₂±1，…，x_n2）

　　　　　b₁=（x₁₂±1，x₂₂，…，x_n2）　　b_n=（x₁₂，x₂₂，…，x_n2±1）

このようにして，点d，e，f，…，hと進み，どの方向に向かっても目的関数zが改善されないとき，その値が最適値と考えられる．このような方法を整数型最大傾斜法とよぶことにする．

なお，制約条件，g（x₁，x₂，…，x_n）≦0がある場合は，傾斜ベクトル（▽f）の制約条件境界線［g（x₁，x₂，…，x_n）＝0］への射影ベクトルの方向で,かつ制約領域内の点をめざして移動して，目的関数の改善の試みを繰り返す．

4.5.4.2　山登りシンプレックス法

また，山登りシンプレックス法（2章p.59）に離散型数値を用いた整数型山登りシンプレックス法を説明しよう．図4.7において3点a（a₁，a₂），b（b₁，b₂），c（c₁，c₂）の値f（a）が最小であるとき，三角形abcの辺bcの反対側の点d（d₁，d₂）をめざす．この例ではd₁= b₁，d₂= c₂である．同様にして，点e，f，g，h，…と移って最適値を求める方法であるが整数型最大傾斜法より劣る．

4.5.4.3　いろいろな最適化

　農作業計画の最適化において，前節のように機械の条件を変える方法だけについても，台数の組合せのシミュレーションのほかに，＊印の作業について台数を増すかわりに能力の高い機械に置き替えて検討するなどの方法がある．このように，システムが多くの条件・要素をもつ場合は，直交配列表を用いた多要因解析法や遺伝アルゴリズム（GA）などの手法を用いると非常に有効であろう。

　また，経営面積（作業面積）を固定して検討する場合には，余裕のある機械作業の能力を下げて（安い機械にかえる）試算することによって，機械利用経費を小さくするように農作業計画の最適化がはかれる．

　実際には，作業期間の調整，作業ピーク時の労働時間延長等のいろいろな条件の改善によって，農作業計画は大きく改善されることがあろう．

　つぎに，農作業計画の目的を経済性ではなく，所要エネルギーの節約であるとした場合の最適化を検討した例を説明する．

　前節のような作業体系において，ha当りのエネルギー消費量（燃料，機械製造エネルギー等を含む）を作業面積との関係にまとめたものが図4.5である．

　この例では，全般に生脱穀を行うコンバインを含む体系（LC）が，バインダ体系のSB，MBセットの場合より所要エネルギーが大きいことを示し，地干し等の太陽熱利用の作業手段によって所要エネルギーを節約できることがわかる．

ここで重要なことは，図4.4，図4.5の比較でわかるように，目的を変えると，すなわち評価関数を変えると最適化も変わっていくということである．したがって，評価関数に金銭的なこと以外の真に必要なものまでも加えていくことが，これからの農作業計画に望まれる．

　また，これらの営農計画に用いられるデータは，その地域の気象，土壌，作物，経営などについての正確な情報でなければならないことはいうまでもない．したがって，それらのデータベースがあれば威力を発揮することになるので，今後農業に関するデータベースはますます重要なものとなろう．

　そのつぎに人工知能（AI）などを用いて農作業データベースを活用するソフトウェア（農作業計画や農作業診断法）を開発していくことが重要である．

　パーソナルコンピュータが各農家にまで普及していくのはそう遠くない将来であると思われるが，今まで以上にグラフィックの手法を生かして図解を増やし，また各圃場単位までの細かい検討のできる農作業計画プログラムが望まれる．

さらに，農作業計画の最適化をはかる場合に，単に経済性だけでなく，労働科学的評価や日曜日はできるだけ休日にするなどの社会的配慮を加えた，本当の意味の目的を設定して，システム設計が行われるようになることを期待したい．そうして，営農計画システムに集大成して，これによって完結するものとなろう．

次章　へ