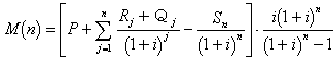4.4.4　農業機械施設の更新　　　　　　　　　　目次（第4章）へ

　●ソフトウェア　EL.exe

　農業経営は単年度で終わるものではないから，長期的な経営について考慮するべきである．

　農業機械施設は使用年数の経過とともにその維持修理費は増大し，処分価格は下落していくので，適当な時期に機械施設の更新を行う必要がある．したがって更新の時期は，その経営体の通年の利益の合計を最大にするように設定されるべきであろう．

　それにはつぎのような機械施設の総費用年価（正味年価：adjusted annual payments of worth）M（n）を算出し，それが最低になる年数（経済寿命とよばれる）のとき更新すればよい．

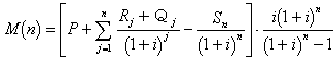　　　　　　　　　eq. 4.61

　ここで，M（n）：n年間使用したときの総費用年価（円／年）

　　　　　 P：取得価格（購入価格）（円）　　　i：年利率

　　　　　 Rj：j年目の修理費（円）

　　　　 Ｑj：j年目の機会損失その他のコスト（円）

　　　　　Sn：n年後の下取価格（残存価格）（円）

　上式の算出式は，つぎのように説明される．

　　　M（n）＝P（n）＋R（n）＋Ｑ（n）−S（n）　　　　　　 eq.4.62

ここで，P（n）：取得価格の年価（円／年）　Ｑ（n）：機会損失その他のコストの

　　　　R（n）：修理費の年価（円／年）　　　　　　年価（円／年）

　　　　S（n）：下取価格の年価（円／年）

　年利率 iを考慮すると，n年後の価格（終価：final worth）Eは，現在の価格（現価：present worth）Pに次式で換算される．

　　　P = E / ( 1 + i ) n　　　　　　　　　　　　　　　 eq. 4.63

　現価 Pの n年目の終価 Eは，（4.64）式から

　　　E＝P（1＋i）n　 　 　 　 　 eq.4.64

　右辺の（1+i）n は，終価係数（final worth factor またはsingle payment, compound amount factor）とよばれる．この逆数は現価係数（present worth factor）とよばれる．

年価とは，ある現価Pをn年間一定の額Mにならして換算したものであるから，n 年間の年価Mの終価EMは，

　　　EM ＝ M * {（1＋ i ）n - 1＋（ 1 + i ）n - 2 ＋ ･･･ ＋（1 + i）＋1 }

　　　　　　 ＝ M * {（1＋ i ）n - 1 } / i　　　　　　　　　　　　　　 eq. 4.65

　したがって，EはEMと等しくなければならないので，（4.64），（4.65）式から

　　　M ＝ P * i * ( 1＋ i ）n / {（1＋ i ）n - 1 }　　　　　　　 eq. 4.66

　本式は現価を年価に換算する一般式である．したがって，

　　　P(n) ＝ P * i * ( 1＋ i ）n / {（1＋ i ）n - 1 }　　　　　　　eq. 4.67

　n年間の修理費の現価合計RTは（4.63）式を用いて，

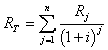　　　　　　　　　　　　　　　　　　　 eq. 4.68

　したがって，修理費の年価R（n）は（4.68）（4.66）式から

　　　R(n) ＝ RT * i * ( 1＋ i ）n / {（1＋ i ）n - 1 }

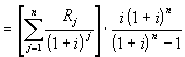　　　　　 　　　　　　　　　eq. 4.69

　（4.65）式の右辺の係数は年金終価係数（uniform series final worth factor）とよばれる．また，この逆数は減債基金係数（sinking fund factor）とよばれる．（4.66）式の右辺の係数は，資本回収係数（capital recovery factor）とよばれる．この逆数は，年金現価係数（uniform series present worth factor）とよばれる．

　機会損失 その他のコストの年価Ｑ（n）も同様にして得られる．

また，下取価格の年価S（n）は（4.63），（4.66）式から

　　　S(n) ＝ Sn * / ( 1＋ i ）n * i * ( 1＋ i ）n / {（1＋ i ）n - 1 }

　　　 　　 ＝ Sn * i / {（1＋ i ）n - 1 }　　　　　　　　　 eq. 4.70

　このように（4.62），（4.67），（4.69），（4.70）式から（4.61）式は誘導されたことがわかる．

コンバインの総費用年価の一例を表4.5に示す．コンバインの修理費は，４年目と７，８年目に大修理を必要としているのが特徴で，機会損失その他のコストを0としたとき，総費用年価は６年目に最低になり（経済寿命は６年），６年目に更新するのがよいことを示している．

　

表4.5　コンバインの総費用年価の一例　(P=500万円，i = 5%）

n P(n) Rn R(n) 　 Sn M(n) 　
年数 取得価格

の年価

 年　間

修理費

 修理費

の年価

 残　存

価格率

 下取価格 総費用年価 　
　 　 　 　 　 　 Ｑ(n)=0の場合 Ｑ(n)=R(n)の場合
　 (千円) (千円) (千円) ％ (千円) (千円) (千円)
1 5250 50 50 65 3250 2050 2100
2 2689 100 74 40 2000 1788 1862
3 1836 150 98 25 1250 1538 1636*
4 1410 1850 505 15 800 1729 2234
5 1155 800 558 10 500 1623 2181
6 985 650 572 4 200 1527* 2099
7 864 2300 784 2 100 1636 2420

　　　　*印は総費用年価が最低であり，経済寿命を示す．

　実際には，故障に伴い作業機会を失ない代替作業経費などの機会損失その他のコストを見積る必要があり，それをＱ（n）＝R（n）［作業機会損失コスト係数 q＝機会損失コスト／修理費＝１］としたとき，総費用年価は３年目に最低になり，３年ごとに更新すると最も経済的であることがわかる．請負作業を含み20ha規模の専業農家の例では３〜４年ごとに更新している実例からみて，大規模農家では作業機会損失コスト係数＝１とするのが妥当と思われる．

　このように，数年間の総利益を最大にする，あるいは数年間の総経費を最小にするようなシステムの最適化は，農業システムではとくに重要と考えられる．すなわち，目先の利益だけでなく，長い年月を通じて全体として最高の結果を導くようなシステム設計が強く望まれる．

次章　へ