2.5.3.3 ディジタル基本回路 目次(第2章)へ
i) 基本論理回路
1) スイッチ:接点を閉じる・開くの2状態にできるスイッチ(switch)は,最も簡単な入力情報回路である.
2) ランプ: ランプ(lamp)の点滅という2状態は,代表的な出力情報回路といえる.
3) リレー: リレー(継電器relay)は,電磁石の働きで,電流によって接点の開閉を行うものであり,入力・出力の両機能に使用できる.
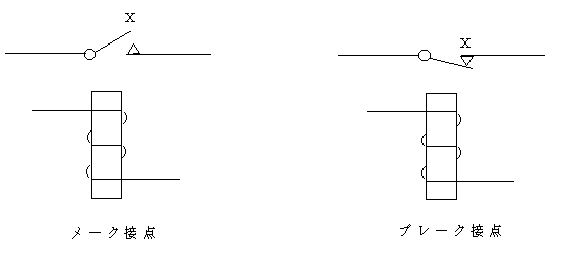
図4.5の左側のように,電流が流れると閉じる接点をメーク接点(make con-tact あるいは a接点),右側のように電流が流れると開くような接点をブレーク接点(break contact あるいはb接点)とよぶ.
スケッチで上から押すことを1,押さないことを0の入力状態(X)に対応させ,接点の開を0,閉を1の出力状態(Y)に対応させると,メーク接点は,Y=X,ブレーク接点では,Y=X ̄を示すことができる.

図2.31 リレーの記号
4) 接点によるANDとOR: 図2.32のように,並列接点回路は,論理和:OR回路を示し,直列接点回路は,論理積:AND回路を示す.
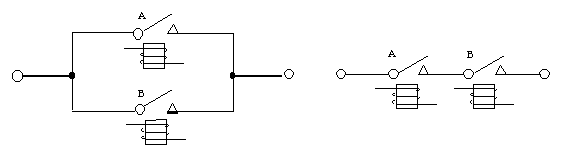
図2.32 接点を用いた論理和回路と論理積回路
5) ゲート回路(gate circuit):トランジスタやダイオードがディジタル情報回路素子として用いられるときは,入出力端子の電位を1・ 0に対応させる.通常,正・負を1・0,または高電位を1,低電位(0V)を0に対応させ,正論理対応とよぶ.この逆の対応を負論理対応とよぶ.(図2.33).
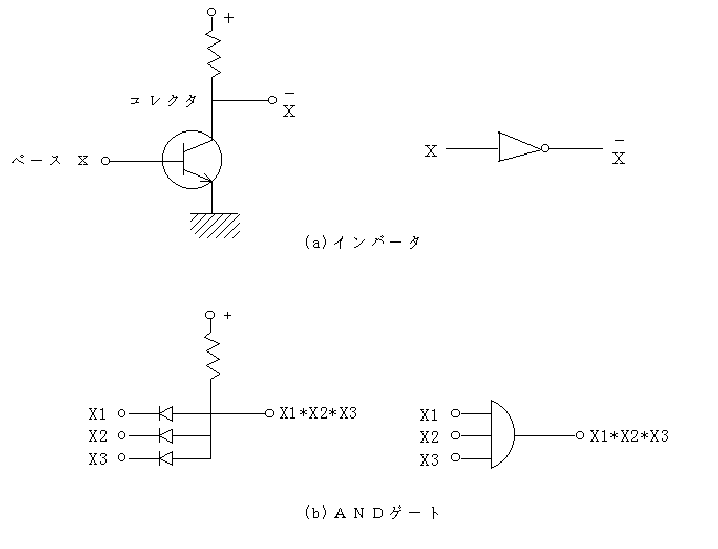
図2.33 インバータとANDゲートの回路例
(a)の否定素子は,トランジスタのベース電位が高いときは,導通状態となってコレクタ電位が低くなり,逆にベース電位が低いときは,非導通状態になってコレクタ電位が高まる現象を利用している.
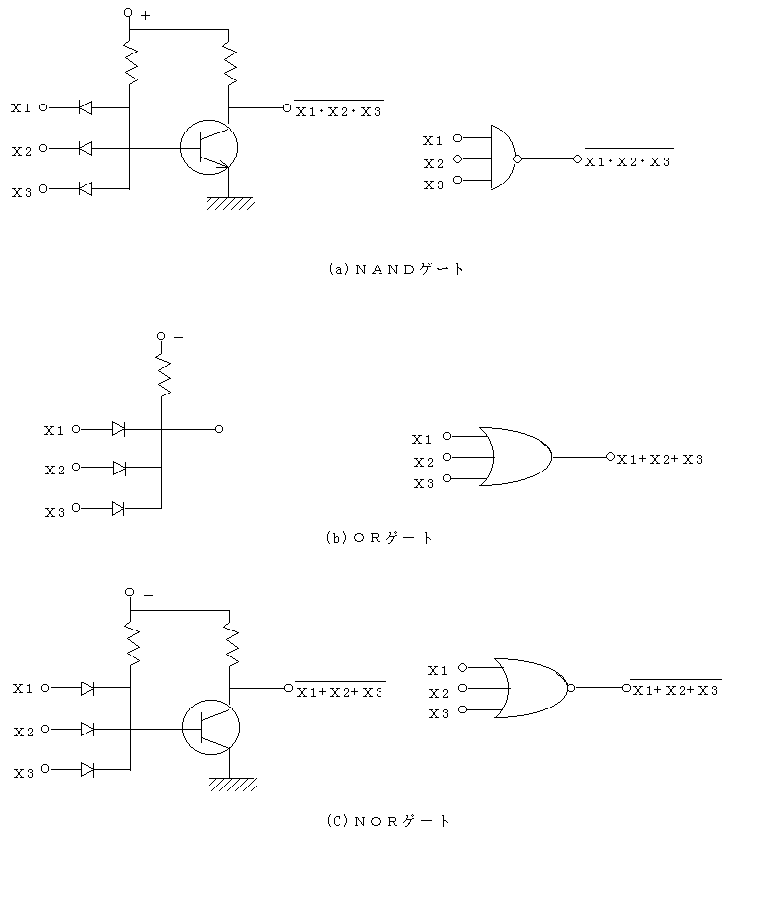
図2.34 NAND・OR・NORゲートの回路例
一方,(b)のAND素子では,X1,X2,X3のいずれか一つが低電位ならば,ダイオードを通じて電流が流れ,出力端子の電位が低くなる現象を利用している.図2.34に,NAND,OR,NOR素子の回路の例を示した.なお,これらのNOT,AND,NAND,OR,NOR素子を用いた回路をゲート回路ともよぶ.シンボル記号は,それぞれの右側に示したとおりである.
ii) 全加算器(full adder)
2進1桁の二つの数をX,Y,その和をS,上位桁への桁上がりをUとすれば,表2.16のような真理値表が得られ,Sは,X,Yの排他的論理和(XOR),Uは,X,YのANDで表されることがわかる.(L=0のとき)
これを,図2.35(a)のような回路で表したものを半加算器(half adder)とよぶ.
1桁以上の加算では,低位桁からの桁上がりをLとすれば,表2.16のような真理値表が得られる.
表2.16 全加算器の真理値表
入力変数 X Y L |
出力変数 S U |
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
0 0 1 0 1 0 0 1 1 0 0 1 0 1 1 1 |
これからSとUを主加法標準展開で求めると,_・
_ _
_ _ _ _
S = X・Y・L + X・Y・L + X・Y・L + X・Y・L
_ _
_ _ _
= L・( X・Y + X・Y ) + L・( X・Y + X・Y )
_
_ _
U = X・Y・L + X・Y・L + X・Y・L + X・Y・L
_
_ _
= X・Y・( L + L ) + L・( X・Y + X・Y )
_
_
= X・Y + + L・( X・Y + X・Y )
となり,これは全加算器の式とよばれる.
L= 0 のとき
_ _
S = X・Y + X・Y
U = X・Y
であり,これが半加算器(図2.35(a))であり,これを用いて,図2.35(b)のように,全加算器の回路を構成することができる.
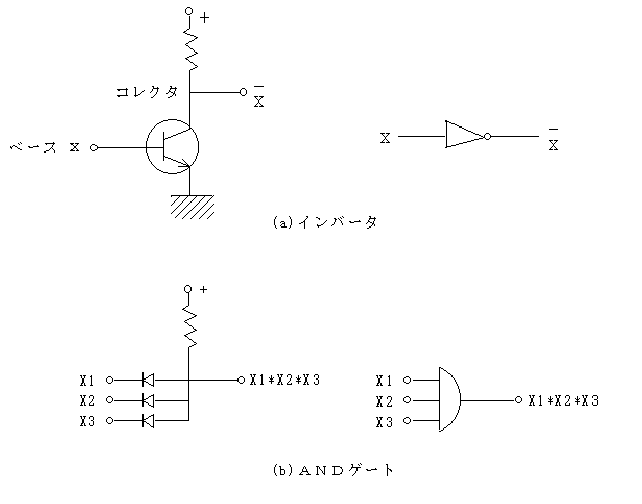
図2.35 半加算器による全加算器の回路
iii)どこからでも点滅できるランプ回路 一つのランプ(あるいはモータ)を,離れた2カ所X,Yから自由に点滅したい場合は多い.これを論理式で表現すると,ランプLに関する真理値表は,つぎの表のとおりで,これを,Lが1である行をXとYの積の形で表し,和をとると(主加法標準展開),
_ _
L = X・Y + X・Y
となる.
X Y |
L |
0 0 1 0 1 1 0 1 |
0 1 0 1 |
これは,いわゆる排他的論理和(XOR)であり,そのスイッチ配線は,3Pスイッチ(transfer switch)2個を,図2.36のように行えばよい.
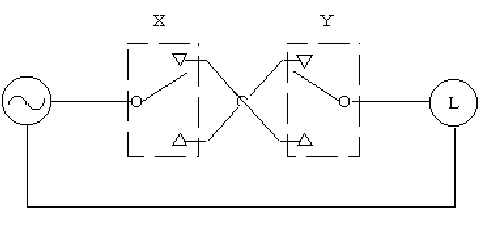
図2.36 2カ所から点滅
iv) 保持回路 論理素子に帰還回路を適用すると,図2.37でX=A+Xと表され,Aが一度1になると,Xは1になり,そのまま保持される.
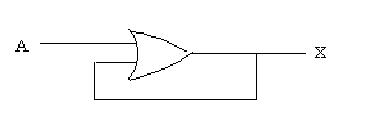
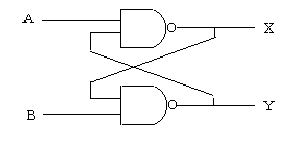
図2.37 保持回路 図2.38 保持およびリセット回路(1)
図2.38では,
__ _ _ __ _ _
X = A・Y = A + Y , Y = B・X = B + X となり,整理すると,
_ _
X = A + B・X , Y = B + A・Yと表され,表2.17の真理値のような値を示し,Xは,Bが0であると,XはA ̄の値を示すが,Bが1であると,A ̄が一度1になるとXは1になり,A ̄が0になってもXはそのまま1を保ち,Xは1を記憶した状態になり,再びBを0にしないかぎりXは0にもどらない.
表2.17 保持回路の真理値表
_ |
A B X Y | _ |
1 0 0 1 0 1 0 |
0 0 1 1 1 0 0 1 1 1 0 1 0 1 1 0 1 1 1 0 0 1 1 0 1 0 0 1 |
0 1 1 0 0 0 1 |
また,図2.38のNAND素子をNOR素子に置きかえると,()
__ _ _ _
X = A・Y = A + Y = A ( B + X )
__ _ _ _
Y = B・X = B + X = B ( A + Y )
と表され,Xは,Aが1であると常に0であるが,Aが0であるとそのときのBの値がXに記憶される.
これらの回路を図2.39,2.40のように変えると,Xはそれぞれつぎのように表される.
_
X = A + B・X )
_
X = B ( A
+ X )
2式とも記憶要素の動作を示す式であるが,上式は,Bが1であってもAを1にすることによってXを1にできるが,下式では,Bが1であるとXは0以外になりえない.
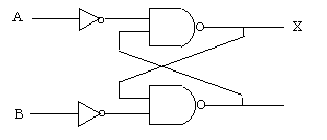
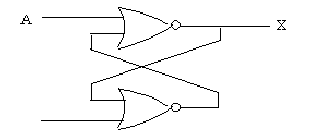
図2.39 保持およびリセット回路(2) 図2.40 リセット優先の保持回路
Aは記憶させる値であり,Bは記憶を解除する条件と考えられるが,上式はA優先であり,下式はB優先の記憶要素の式といえよう.
これらは,変化信号制御系の信号保持や,モータの駆動保持などの回路に応用されるが,後者の場合で上の2式の差を考えると,上式は,スタート優先の回路となるが,下式は,ストップ優先の回路になるといえる.
v) フリップフロップ回路(flip flop circuit)フリップフロップ回路は,二つの安定点をもち,入力信号の内容によってどちらの安定点をとるかが決まる記憶回路で,図2.41のように,出力の一方をQとすると,他方はその否定のQ ̄となる.
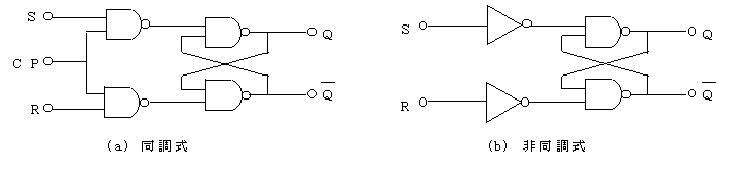
図2.41 R−Sフリップフロップ
R−Sフリップフロップ(R:reset,S:set)の真理値表は,下表のとおりである.
R S |
Qn + 1(R,Sに信号を与えた後の状態) |
0 0 0 1 1 0 1 1 |
Qn:(Qn + 1の1ステップ前の状態) 1 0 不定 |
vi) シフトレジスタとカウンタ
1) シフトレジスタ: ディジタルの演算装置で,演算数,被演算数やその結果などの二進情報を記憶したり,記憶された情報を右や左に送る装置がシフトレジスタ(shift register)である.
前述のようにフリップフロップが1ビットの2進情報を記憶できるので,必要なビット数だけのフリップフロップを直列接続することによってシフトレジスタを構成することができる.
2) カウンタ: カウンタ(counter)はパルスの数を計算するもので,ディジタル回路では欠くことのできない回路である.
カウンタにはフリップフロップが構成素子として使用され,一つのフリップフロップ回路では2進数1桁の計数が行える.このことからフリップフロップによるカウンタはバイナリーカウンタ(binary counter)とよばれる.
vii) 優先回路
1) 優先回路(固定):図2.42において,乾燥機への上部シャッタY41〜Y48を,Y41〜Y48の順に優先して1カ所開く動作の論理式yiは次のようになる.
y41 = f41
_
y42 = Y41
・ f42
_ _
y43 = Y41・
Y42・
f43
・
・
・
_ _ _ _ _ _ _
y48 = Y41・
Y42・Y43・
Y44・Y45・
Y46・Y47・
f48
ただし,fiは,おのおのの上部シャッタの解放可能な条件
Yiは開状態のとき1,閉状態のとき0である.
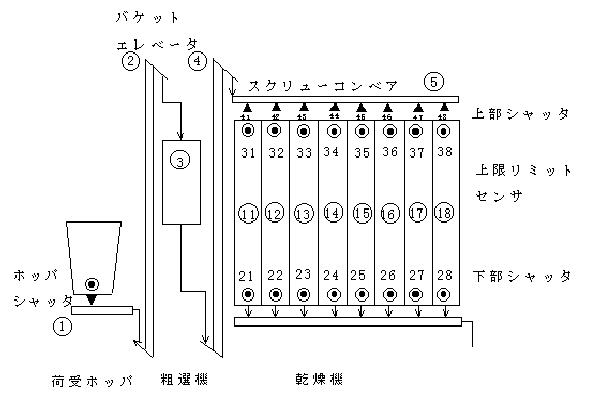
図2.42 ライスセンタ(受入れから乾燥機まで)
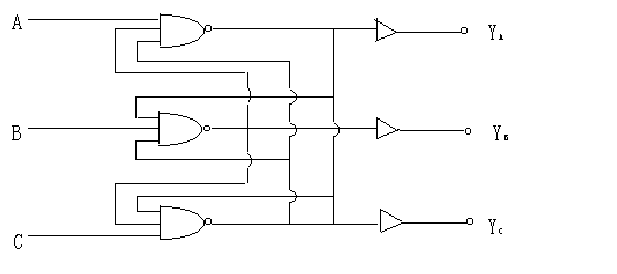
図2.43 先着優先回路
2) 先着優先回路: A,B,Cの3信号のうち,先着した信号のみを伝える信号は,図2.43のNANDゲートによって得られ,つぎのようになる.
_ _
YA =
A ・ YB・
YC
_ _
YB =
B ・ YA・
YC
_ _
YC =
C ・ YA・
YB
まとめて,1信号の回路にするのならば,
Y=YA+YB+YC
のようにすればよい.
viii) 遅れ回路
遅れ要素のある帰還回路を,図2.44(a)のように構成すると,
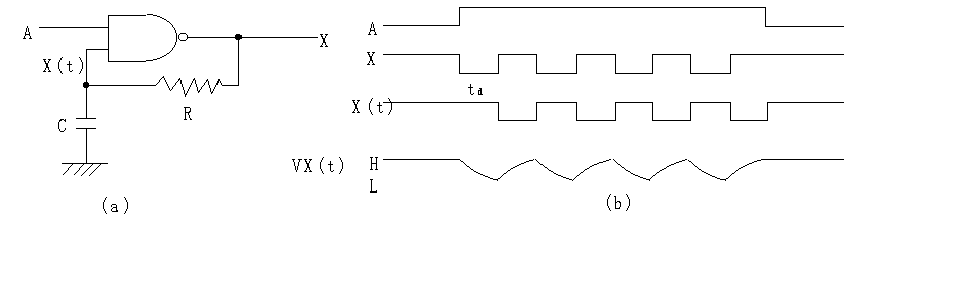
図2.44 おくれ回路
____ _ __
X = A ・
X(t) = A + X(t)
そのタイムチャートを描くと(b)図のように,X(t)はt d(時定数CR)だけXに遅れて動作し,Aが1であるかぎりXもX(t)にt dだけ遅れて発振状態に入り,Aが0になるまで続く.