2.5.3.2 論理代数 目次(第2章)へ
i) 論理式 論理関数は,論理和+,論理積・,否定 ̄の三つの演算
で表しうる.
このような論理式を扱う代数は論理代数(logical Algebra)またはブール代数(Boolean algebra)とよばれ,つぎのような恒等式が成り立つ.
ii) 交換の定理
X + Y = Y + X
X・Y = Y・X
iii) 結合の定理
(X + Y) + Z = X +(Y + Z)
(X・Y)・Z = X・(Y・Z)
iv) 分配の定理
X・X・(Y + Z)= X・Y + X・Z
X + Y・Z =(X + Y)・(X + Z)
v) べき等の定理
X + X = X
X・X = X
vi) ド・モルガンの法則(De Morgan law)
___ _ _
X + Y
= X ・Y
___ _ _
X ・Y
= X
+ Y
vii) 0と1を含む吸収の定理
X + 0 = X X + 1 = 1
_
X・1
= X X + X = 1
_
X・0
= 0 X・X = 0
viii) 二重否定
=
(X)
= X
ix) 吸収律の定理
X + X・Y = X
X・(X + Y)= X
_
X +
X・Y = X + Y
_
X・
( X + Y )= X・Y
なお,論理式が成立するという証明には,変数のあらゆる組合せに対する左辺・右辺のそれぞれの値が等しいことを示す方法が簡便である.たとえば,
_
X +
X・Y = X + Yの証明には,X,Yの組合せはつぎの表のように4通りしかなく,簡単に証明できる.
X Y |
左辺の値 右辺の値 |
0 0 0 1 1 0 1 1 |
0 0 1 1 1 1 1 1 |
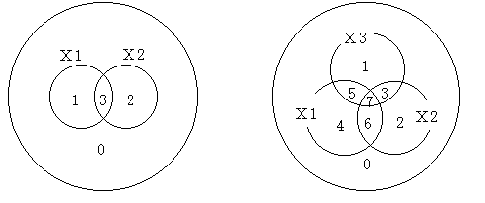
x) フェン図 論理関数は,真理値表でも表現できたが,直観的に示すには図2.27のようなフェン図(Venn diagram)がよく用いられる.

図2.27 フェン図
xi) 論理式の簡単化
1) 論理式の変形による方法:
〔例題〕次式を簡単にせよ.
_ _ _ _ _ _
_ _ _ _
_ _ _ _ _ _
Y = A B C
D + A B C D + A B C D + A B C D +A
B C D +A B C D + A B C D
〔解〕
_ _ _ _ _
_ _ _ _
_ _
Y = A B D
(C +C) + A B D (C +C)
+ A B C (D +D ) D + A C D
( B + B )
_ _ _ _
_ _ _
= A B D + A B D + A B C + A
C D
_ _ _
_ _
= A ( B D + B D )+ A C (
B + D )
2) カルノー図表による方法: 一般に,論理関数は,図2.28のようなカルノー図表(Karnaugh map)に示すことができる.
カルノー図表の特徴は,ただ1個の変数だけが異なる基本積に対応する領域は必ず隣接していることである.したがって,
_
X + X = 1 の関係を用いれば,カルノー図表上で互いに隣接する二つの基本積は必ず一つにまとめることができ,しかもそのとき変数の数を一つ減らすことができる.
〔例題〕図2.29に示される論理式Yを簡単にせよ.
〔解〕図2.29より,
_ _ _ _
_ _ _ _ _
_ _ _ _ _
Y = A B C
D + A B C D + A B C D + A B C D +A
B C D +A B C D + A B C D
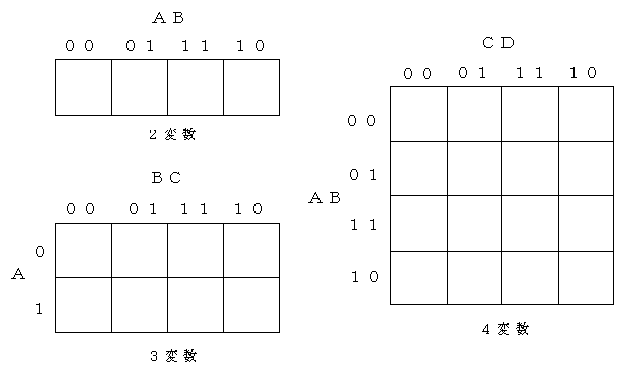
図2.28 カルノー図表
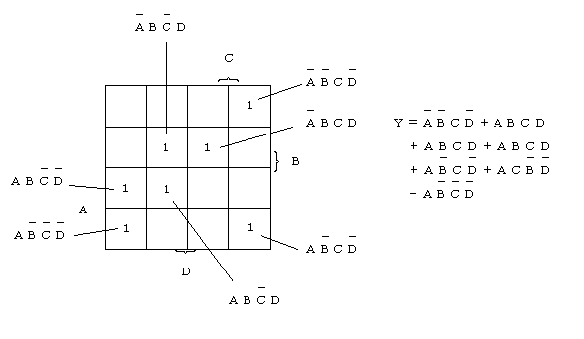
図2.29 カルノー図表による論理関数
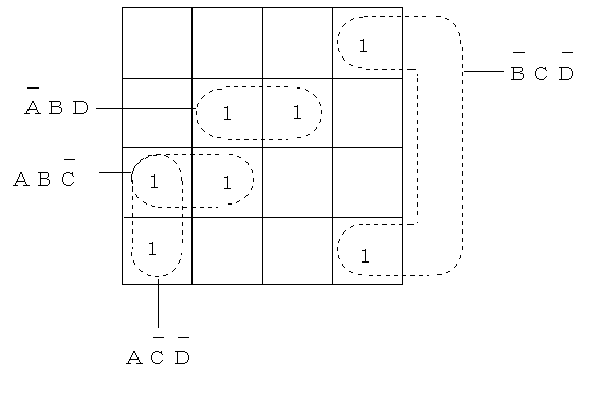
図2.30 カルノー図表によるまとめ方
図2.30より,
_ _ _
_ _ _
Y = B C D
+ A B D + A B C + A C D
_ _ _ _
_ _
= B C D + A B D + A C ( B
+ D )