作業手順
2.4.5 動的計画法 目次(第2章)へ
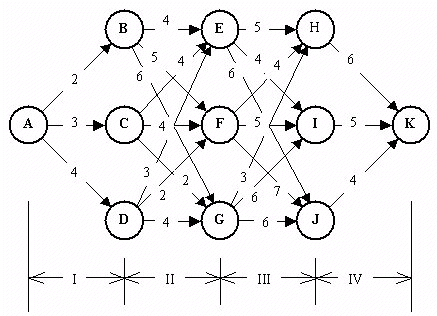
図2.24のように,ある農作業で4回のシリーズの作業が必要であり,それぞれ使用する農業機械によって矢印で示される順序が決められていて所要時間が示されている.A点からK点までの一連の作業を最短時間で行うのは,どの作業シリーズを選べばよいか.

作業手順
図2.24 A時点からK時点までの農作業シリーズ
すべての一連の作業の所要時間を計算して比較すると,(A−C)1+(C−G)2+(G−H)3+(H−K)4 = 14時間が最短であることがわかる.
このようにすべての所要時間を計算する方法は,作業の種類nが増大した場合3n−1で表されるようにその組合せは急激に増大し,膨大な計算時間を要しきわめて効率がわるくなる.この問題をよくみると作業が4段階になっている多段階決定問題であり,ある一時点でのみについての選択だけでなく,全期間にわたってつぎつぎに選択して,一連の選択の効果が全期間を通じて最適になるように決定する問題である.開始点Aから出発して考えると第一の作業はA−B,A−C,A−Dの3種がある.E時点へはABE,ACE,ADEの3通りあるがそれぞれ6,7,7でABEが最短である.F時点へはABF,ACF,ADFの3通りあるがそれぞれ7,7,6でADFが最短であり,同様にG時点へはACGが5で最短である.
つぎに第3の作業を行うが,H時点ではE,F,Gの3時点までの所要時間と第3作業の所要時間の和を考えるが,すでにAE間はABEが,AF間はADFが,AG間はACGが最短とわかっているのでその値を用いればよい.したがって,H時点では,“ABE+5,ADF+4,ACG+3”の3通りを計算して11,10,8が得られ,ACGHが最短である.I時点では,ABE+4,ADF+5,ACG+6から10,11,11が得られ,ABEIが最短である.同様に,J時点ではACGJが11で最短である.
最終的にK時点では,ACGH+6,ACGI+5,ACGJ+4を比較してACGHKの作業シリーズが最短時間14をもたらすことがわかる.
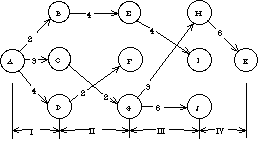
この方法を図示したのが図2.25であり,各作業ごとに最短でない手順を取り除いたものである.
作業手順
図2.25 不用の手順を取り除いた農作業シリーズ
●ソフトウェア DP1.exe
このように,ある段階まで作業したら,その時点ではそれまでどの作業を行うと最短時間で行うことができるかがわかっているので,その時点から前のあらゆる組合せの計算を行う必要がなく効率よく最適解を求めることができる.これは動的計画法(dynamic programming)とよばれ,システム解析の計算手法の一つである.
このように開始点から終了点まで前進しながら最適解を求める方法を前進法とよび,数式で表すとつぎのようになる.
T1(B)= 2,T1(C)= 3,T1(D)= 4 eq. 2.93
T2(E)= min [T1(B)+ 4,T1(C)+4,T1(D)+3]
= min [2 + 4,3 + 4,4 + 3]= 6 eq. 2.94
T2(F)= min [T1(B)+ 5,T1(C)+4,T1(D)+2]
= min [2 + 5,3 + 4,4 + 2] = 6 eq. 2.95
T2(G)= min [T1(B)+ 6,T1(C)+2,T1(D)+4]
= min [2 + 6,3 + 2,4 + 4] = 5 eq. 2.96
T3(H)= min [T2(E)+5,T2(F)+ 4,T2(G)+ 3]
= min[6 + 5,6 + 4,5 + 3] = 8 eq. 2.97
T3(I)= min [T2(E)+ 4,T2(F)+ 5,T2(G)+6]
= min [6 + 4,6 + 5,5 + 6] = 10 eq. 2.98
T3(J)= min [T2(E)+ 6,T2(F)+ 7,T2(G)+ 6]
= min [ 6 + 6,6 + 7,5 + 6] = 11 eq. 2.99
T4(K)= min [T3(H)+ 6,T3(I)+ 5,T3(J)+ 4]
= min [ 8 + 6,10 + 5,11 + 4] = 14
=T(ACGHK) eq. 2.100
なお,終了点から開始点へ向かう方向でも同様に最適解が求められ,それを後退法という.
これを一般式で示すと,あるn時点までの最適値をFn(X)で表し,初期時点でx1作業を行ったときの所要時間をf(x1)とすると,
F1(X)= f(x1) eq. 2.101
つぎにF2(X)については,x2 作業を行ってx1 作業までの最適値F1(X)との和を最小にすればよい.すなわち,
F2(X)=
min { F1(X)+ f(x2)} eq. 2.102
x2
同様にして,xn作業を行うときは,
Fn(X)=
min { Fn−1(X)+ f(xn)}
eq. 2.103
xn
Fn(X)はnについて前式のように漸化式が成立するが,これはベルマン(Bellman)の最適性の原理(principle of optimality)とよばれる.
JIS(Z8121)によると,最適性の原理とは,「決定の全系列にわたり最適化を行うには,ある段階での決定がどうあろうとも,その決定から生ずる状態に関して残りの段階での決定が最適決定でなければならないという原理」である.