2.4.4.3 山くずし法 目次(第2章)へ
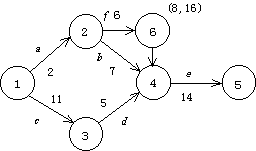
農作業システムのスケジュールを考えるとき,作業に必要な人員配置は重要な問題である.図2.21のアローダイヤグラムで示される作業に必要な人員を,すべての作業を最早着手日に開始する場合について山積表で示すと図2.22のように最大7人の人員を要することになる.

図2.21 アローダイヤグラム
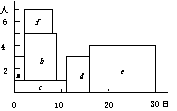
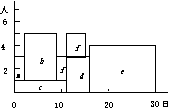
図2.22 人員の山積み法 図2.23 山くずし法
表2.11 所 要 人 員
作業 |
所要 日数 D |
所要 人員 M |
最 早 着手日 E |
最 遅 着手日 L |
総 余裕 T |
自由 余裕 F |
独立 余裕 I |
a b c* d* e* f |
2 7 11 5 14 6 |
2 4 1 3 4 2 |
0 2 0 11 16 2 |
7 9 0 11 16 10 |
7 7 0 0 0 8 |
0 7 0 0 0 8 |
0 0 0 0 0 8 |
*はクリティカル・パスを示す.
ここで作業fを6日後へずらすと図2.23のように最大5人の人員で全作業を行うことができる.このような調整方法を山くずし法(leveling)とよぶ.
山くずし法によって人員配置の平均化を行う場合に,表2.11に示す最早着手日E,最遅着手日L,総余裕T,自由余裕F,独立余裕Iを用いるとよい.
最早着手日は,作業システムを開始してから各作業をできるだけ前へとつめたときに着手可能となる日である.
最遅着手日は,各作業の終了をクリティカル・パス上の作業に間に合うかぎりできるだけ遅く開始できる日である.クリティカル・パス上の作業では最早着手日と最遅着手日は一致している.
総余裕T(total float)は,他作業を可能なかぎり前後に動かしたとき得られる最大の余裕日数である.
T =(後続作業のL)−(本作業のE)−(本作業の所要日数D)
自由余裕F(free float)は,後続作業は最早に着手し,先行作業はできるだけ前につめたいとき得られる日数である.
F =(後続作業のE)−(本作業のE)−(本作業の所要日数D)
独立余裕I(independent float)は,他の作業に影響を与えず自由にえらべる余裕日数である.
I =(後続作業のE)−(先行作業のL)−(先行作業の所要日数D)
−(本作業の所要日数D)
また,T≧F≧Iで,山くずしはまずこれらの余裕日数の範囲で行うとよい.
図2.22から図2.23へは,全体の所要日数を変えることなく最大所要人数を7人から5人へ減らすことができたが,これを4人に減らすには全日程を延長するか各作業の所要人数を減らすかの手段が必要になる.
農作業などでは通常日程を延長することは収量の減少につながるので,能率のよい機械を導入して作業の所要人数を減らす方法が用いられることが多い.そのような場合に用いられる方法の一つがCPMである.